人教版八年级数学上册试题 11.1.2 《三角形的高、中线和角平分线》同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学上册试题 11.1.2 《三角形的高、中线和角平分线》同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 824.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 18:54:00 | ||
图片预览

文档简介
11.1.2 《三角形的高、中线和角平分线》
一、单选题
1.下列多边形具有稳定性的是( )
A. B. C. D.
2.请你量一量如图中边上的高的长度,下列最接近的是( )
A. B. C. D.
3.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
4.如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是ABC的AC边上的高线 B.线段CD是ABC的AB边上的高线
C.线段AD是ABC的BC边上的高线 D.线段AD是ABC的AC边上的高线
5.如图,中,,根据尺规作图的痕迹判断以下结论错误的是( )
A. B. C. D.
6.如图,的面积为30,,E为的中点,则 ADE的面积等于( )
A.15 B.12 C.10 D.9
7.如图,是中线,,.若的周长为10,则的周长为( )
A.8 B.9 C.10 D.11
8.如图,在四边形中,,对角线相交于点E,若,,则四边形的面积为( )
A. B. C. D.
9.如图,,,分别是的中线,角平分线,高,下列各式中错误的是( )
A. B.
C. D.
10.在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________.
12.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF值为____________.
13.如图,在中,是中线的中点.若的面积是1,则的面积是______.
14.如图,是的中线,若,,则与的周长之差为____________.
15如图所示的网格是正方形网格,点A,B,C,D均在格点上,则__________ (填“>”,“<”或“=”).
16.如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=______°.
17.如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=2.5cm,则的值为 .
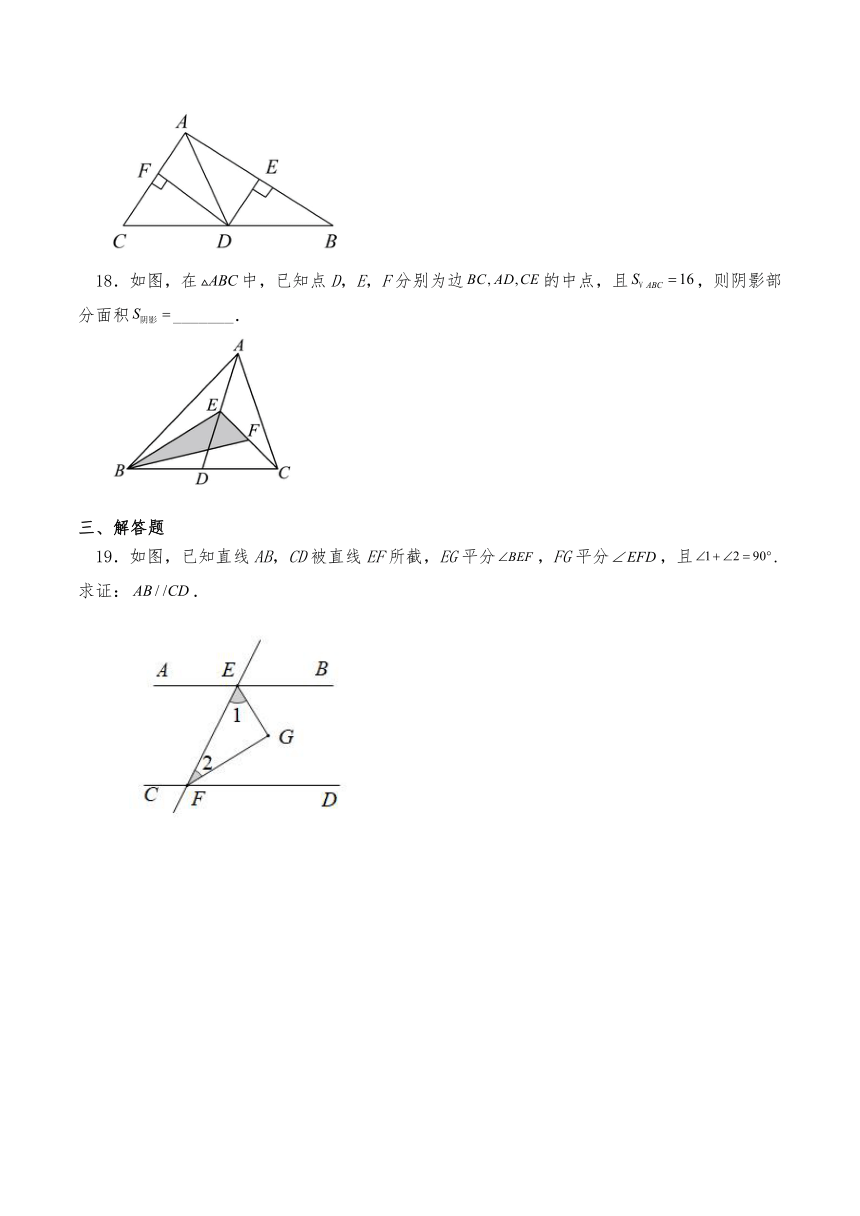
18.如图,在中,已知点D,E,F分别为边的中点,且,则阴影部分面积_______.
三、解答题
19.如图,已知直线AB,CD被直线EF所截,EG平分,FG平分,且.求证:.
20.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
21.如图,在△ABC中,AD平分∠BAC交BC于点D,过点D作DE∥AB交AC于点E.
求证:AE=DE.
22.【图形定义】
有一条高线相等的两个三角形称为等高三角形.
例如:如图①.在和中,分别是和边上的高线,且,则和是等高三角形.
【性质探究】
如图①,用,分别表示和的面积.
则,
∵
∴.
【性质应用】
如图②,D是的边上的一点.若,则__________;
如图③,在中,D,E分别是和边上的点.若,,,则__________,_________;
如图③,在中,D,E分别是和边上的点,若,,,则__________.
23.如图,中,,,,.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
(1) 当t=___________时,把的周长分成相等的两部分?
(2) 当t=___________时,把的面积分成相等的两部分?
(3) 当t为何值时,的面积为12?
24.阅读下列材料,并完成相应的任务.
古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S=(其中a,b,c是三角形的三边长,,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴=6
∴S===6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
根据上述材料,解答下列问题:
如图,在△ABC中,BC=7,AC=8,AB=9
(1)用海伦公式求△ABC的面积;
(2)如图,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.
答案
一、单选题
1.D
【分析】利用三角形具有稳定性直接得出答案.
解:三角形具有稳定性,四边形、五边形、六边形都具有不稳定性,
故选D.
2.D
【分析】作出三角形的高,然后利用刻度尺量取即可.
解:如图所示,过点A作AO⊥BC,
用刻度尺直接量得AO更接近2cm,
故选:D.
3.D
【分析】根据折叠的性质可得,作出选择即可.
解:如图,
∵由折叠的性质可知,
∴AD是的角平分线,
故选:D.
4.B
【分析】根据高线的定义注意判断即可.
解:∵ 线段CD是ABC的AB边上的高线,
∴A错误,不符合题意;
∵ 线段CD是ABC的AB边上的高线,
∴B正确,符合题意;
∵ 线段AD是ACD的CD边上的高线,
∴C错误,不符合题意;
∵线段AD是ACD的CD边上的高线,
∴D错误,不符合题意;
故选B.
5.D
【分析】由尺规作图可知AD是∠CAB角平分线,DE⊥AC,由此逐一分析即可求解.
解:由尺规作图可知,AD是∠CAB角平分线,DE⊥AC,
在△AED和△ABD中:
∵,∴△AED≌△ABD(AAS),
∴DB=DE,AB=AE,选项A、B都正确,
又在Rt△EDC中,∠EDC=90°-∠C,
在Rt△ABC中,∠BAC=90°-∠C,
∴∠EDC=∠BAC,选项C正确,
选项D,题目中缺少条件证明,故选项D错误.
故选:D.
6.C
【分析】根据三角形的中线的性质与面积公式即可得到结论.
解:∵的面积为30,,
∴,
又E为的中点,
∴.
故选:C.
7.D
【分析】根据中线的定义可得,结合的周长可得,进而得出,即可求解.
解:∵是中线,
∴,
∵的周长为10,,
∴,
∴,
∴的周长为,
故选:D.
8.A
【分析】由四边形中, ,可得,再利用,,然后可求出,根据可得,从而可得答案.
解:∵四边形中, ,
∴,
∵,
∴,
∴,
∵
∴,
∴.
故选:A.
9.D
【分析】根据三角形的高线,角平分线和中线解答即可;
解:A.∵是的中线
∴,
故选项正确,不符合题意;
B.∵是的角平分线
∴
故选项正确,不符合题意;
C.∵分别是的高,
∴
故选项正确,不符合题意;
D.不一定成立,故选项错误,符合题意.
故选:D.
10.D
【分析】根据三角形中线的定义可直接得出答案.
解:是的中线,
点D为边的中点,
,
因此丁同学的结论正确,
故选:D.
二、填空题
11.三角形具有稳定性
【分析】根据三角形结构具有稳定性作答即可.
解:其数学道理是三角形结构具有稳定性.
故答案为:三角形具有稳定性.
12.
【分析】由题意得:BF⊥AC,再根据三角形的面积公式,可得,进而即可得到答案.
解:∵在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,
∴BF⊥AC,
∵AB=5,BC=4,AC=6,
∴,
∴,
∴CE:AD:BF=,
故答案是:.
13.2
【分析】根据的面积的面积,的面积的面积计算出各部分三角形的面积.
解:是边上的中线,为的中点,
根据等底同高可知,的面积的面积,
的面积的面积的面积,
故答案为:2.
14.1
【分析】利用三角形的中线的定义可知,所以两个三角形的周长差即为.
解:∵,,
∴.
又∵是中线,
∴,
∵,,
∴.
故答案为:1.
15.<
解:由题意,
,
,
∴;
故答案为:<.
16.50
【分析】根据折叠的性质求得∠CDE=∠CDA=70°,得到∠BDE=40°,再利用余角的性质即可求解.
解:根据折叠的性质得:∠CDE=∠CDA=70°,∠CED=∠A=90°,
∴∠BDE=180°-70°-70°=40°,∠BED=180°-90°=90°,
∴∠B=180°-90°-40°=50°,
故答案为:50.
17.
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
解:∵△ABC中,AD为中线,
∴BD=DC.
∴S△ABD=S△ADC.
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=2.5.
∴ AB ED= AC DF,
∴×6×ED=×2.5×DF,
∴.
故答案为:.
18.4
解:∵点D为中点,
∴,
∵点E为中点,
∴,,
∴,
∵点F为中点,
∴.
故答案为:4.
三、解答题
19.
解:因为EG平分,FG平分(已知),
所以,(角平分线的定义),
所以(等式的性质).
又因为(已知),
所以,
所以(同旁内角互补,两直线平行).
20.60°
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.
解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED-∠B=85°-50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
三、解答题
21.
解:∵AD平分∠BAC交BC于点D,
∴∠BAD=∠EAD,
∵DE∥AB,
∴∠BAD=∠ADE,
∴∠EAD=∠ADE,
∴AE=DE.
22.
(1)解:如图,过点A作AE⊥BC,
则,
∵AE=AE,
∴.
(2)解:∵和是等高三角形,
∴,
∴;
∵和是等高三角形,
∴,
∴.
(3)解:∵和是等高三角形,
∴,
∴;
∵和是等高三角形,
∴,
∴.
23.
解:(1)中,∵,,,
∴的周长,
∴当把的周长分成相等的两部分时,点P在上,此时,
∴,
解得.
故答案为:6;
(2)当点P在中点时,把的面积分成相等的两部分,此时,
∴,
解得.
故答案为:6.5;
(3)分两种情况:
①当P在上时,
∵的面积=12,
∴,
∴,
∴,;
②当P在上时,
∵的面积=12=面积的一半,
∴P为中点,
∴,.
故t为2或6.5秒时,的面积为12.
24.
解:(1)∵BC=7,AC=8,AB=9,
∴
答:△ABC面积是;
(2)如图,过点I作IF⊥AB、IG⊥AC、IH⊥BC,垂足分别为点F、G、H,
∵AD、BE分别为△ABC的角平分线,
∴IF=IH=IG,
∵S△ABC=S△ABI+S△ACI+S△BCI,
∴(9 IF+8 IF+7 IF)=
解得IF=
故S△ABI=AB FI=×9×=.
一、单选题
1.下列多边形具有稳定性的是( )
A. B. C. D.
2.请你量一量如图中边上的高的长度,下列最接近的是( )
A. B. C. D.
3.如图,将△ABC折叠,使AC边落在AB边上,展开后得到折痕l,则l是△ABC的( )
A.中线 B.中位线 C.高线 D.角平分线
4.如图,CD⊥AB于点D,已知∠ABC是钝角,则( )
A.线段CD是ABC的AC边上的高线 B.线段CD是ABC的AB边上的高线
C.线段AD是ABC的BC边上的高线 D.线段AD是ABC的AC边上的高线
5.如图,中,,根据尺规作图的痕迹判断以下结论错误的是( )
A. B. C. D.
6.如图,的面积为30,,E为的中点,则 ADE的面积等于( )
A.15 B.12 C.10 D.9
7.如图,是中线,,.若的周长为10,则的周长为( )
A.8 B.9 C.10 D.11
8.如图,在四边形中,,对角线相交于点E,若,,则四边形的面积为( )
A. B. C. D.
9.如图,,,分别是的中线,角平分线,高,下列各式中错误的是( )
A. B.
C. D.
10.在中,是的中线.看到图形,甲、乙、丙、丁四名同学给出四个不同的结论,其中正确的是( )
甲:
乙:
丙:
丁:
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图,钢架桥的设计中采用了三角形的结构,其数学道理是__________.
12.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,连接BO并延长交AC于点F,若AB=5,BC=4,AC=6,则CE:AD:BF值为____________.
13.如图,在中,是中线的中点.若的面积是1,则的面积是______.
14.如图,是的中线,若,,则与的周长之差为____________.
15如图所示的网格是正方形网格,点A,B,C,D均在格点上,则__________ (填“>”,“<”或“=”).
16.如图,将直角三角形纸片ABC进行折叠,使直角顶点A落在斜边BC上的点E处,并使折痕经过点C,得到折痕CD.若∠CDE=70°,则∠B=______°.
17.如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=2.5cm,则的值为 .
18.如图,在中,已知点D,E,F分别为边的中点,且,则阴影部分面积_______.
三、解答题
19.如图,已知直线AB,CD被直线EF所截,EG平分,FG平分,且.求证:.
20.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
21.如图,在△ABC中,AD平分∠BAC交BC于点D,过点D作DE∥AB交AC于点E.
求证:AE=DE.
22.【图形定义】
有一条高线相等的两个三角形称为等高三角形.
例如:如图①.在和中,分别是和边上的高线,且,则和是等高三角形.
【性质探究】
如图①,用,分别表示和的面积.
则,
∵
∴.
【性质应用】
如图②,D是的边上的一点.若,则__________;
如图③,在中,D,E分别是和边上的点.若,,,则__________,_________;
如图③,在中,D,E分别是和边上的点,若,,,则__________.
23.如图,中,,,,.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
(1) 当t=___________时,把的周长分成相等的两部分?
(2) 当t=___________时,把的面积分成相等的两部分?
(3) 当t为何值时,的面积为12?
24.阅读下列材料,并完成相应的任务.
古希腊的几何学家海伦在他的著作《度量论》一书中给出了利用三角形三边之长求面积的公式﹣﹣﹣﹣海伦公式S=(其中a,b,c是三角形的三边长,,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴=6
∴S===6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
根据上述材料,解答下列问题:
如图,在△ABC中,BC=7,AC=8,AB=9
(1)用海伦公式求△ABC的面积;
(2)如图,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.
答案
一、单选题
1.D
【分析】利用三角形具有稳定性直接得出答案.
解:三角形具有稳定性,四边形、五边形、六边形都具有不稳定性,
故选D.
2.D
【分析】作出三角形的高,然后利用刻度尺量取即可.
解:如图所示,过点A作AO⊥BC,
用刻度尺直接量得AO更接近2cm,
故选:D.
3.D
【分析】根据折叠的性质可得,作出选择即可.
解:如图,
∵由折叠的性质可知,
∴AD是的角平分线,
故选:D.
4.B
【分析】根据高线的定义注意判断即可.
解:∵ 线段CD是ABC的AB边上的高线,
∴A错误,不符合题意;
∵ 线段CD是ABC的AB边上的高线,
∴B正确,符合题意;
∵ 线段AD是ACD的CD边上的高线,
∴C错误,不符合题意;
∵线段AD是ACD的CD边上的高线,
∴D错误,不符合题意;
故选B.
5.D
【分析】由尺规作图可知AD是∠CAB角平分线,DE⊥AC,由此逐一分析即可求解.
解:由尺规作图可知,AD是∠CAB角平分线,DE⊥AC,
在△AED和△ABD中:
∵,∴△AED≌△ABD(AAS),
∴DB=DE,AB=AE,选项A、B都正确,
又在Rt△EDC中,∠EDC=90°-∠C,
在Rt△ABC中,∠BAC=90°-∠C,
∴∠EDC=∠BAC,选项C正确,
选项D,题目中缺少条件证明,故选项D错误.
故选:D.
6.C
【分析】根据三角形的中线的性质与面积公式即可得到结论.
解:∵的面积为30,,
∴,
又E为的中点,
∴.
故选:C.
7.D
【分析】根据中线的定义可得,结合的周长可得,进而得出,即可求解.
解:∵是中线,
∴,
∵的周长为10,,
∴,
∴,
∴的周长为,
故选:D.
8.A
【分析】由四边形中, ,可得,再利用,,然后可求出,根据可得,从而可得答案.
解:∵四边形中, ,
∴,
∵,
∴,
∴,
∵
∴,
∴.
故选:A.
9.D
【分析】根据三角形的高线,角平分线和中线解答即可;
解:A.∵是的中线
∴,
故选项正确,不符合题意;
B.∵是的角平分线
∴
故选项正确,不符合题意;
C.∵分别是的高,
∴
故选项正确,不符合题意;
D.不一定成立,故选项错误,符合题意.
故选:D.
10.D
【分析】根据三角形中线的定义可直接得出答案.
解:是的中线,
点D为边的中点,
,
因此丁同学的结论正确,
故选:D.
二、填空题
11.三角形具有稳定性
【分析】根据三角形结构具有稳定性作答即可.
解:其数学道理是三角形结构具有稳定性.
故答案为:三角形具有稳定性.
12.
【分析】由题意得:BF⊥AC,再根据三角形的面积公式,可得,进而即可得到答案.
解:∵在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D和点E,AD与CE交于点O,
∴BF⊥AC,
∵AB=5,BC=4,AC=6,
∴,
∴,
∴CE:AD:BF=,
故答案是:.
13.2
【分析】根据的面积的面积,的面积的面积计算出各部分三角形的面积.
解:是边上的中线,为的中点,
根据等底同高可知,的面积的面积,
的面积的面积的面积,
故答案为:2.
14.1
【分析】利用三角形的中线的定义可知,所以两个三角形的周长差即为.
解:∵,,
∴.
又∵是中线,
∴,
∵,,
∴.
故答案为:1.
15.<
解:由题意,
,
,
∴;
故答案为:<.
16.50
【分析】根据折叠的性质求得∠CDE=∠CDA=70°,得到∠BDE=40°,再利用余角的性质即可求解.
解:根据折叠的性质得:∠CDE=∠CDA=70°,∠CED=∠A=90°,
∴∠BDE=180°-70°-70°=40°,∠BED=180°-90°=90°,
∴∠B=180°-90°-40°=50°,
故答案为:50.
17.
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
解:∵△ABC中,AD为中线,
∴BD=DC.
∴S△ABD=S△ADC.
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=2.5.
∴ AB ED= AC DF,
∴×6×ED=×2.5×DF,
∴.
故答案为:.
18.4
解:∵点D为中点,
∴,
∵点E为中点,
∴,,
∴,
∵点F为中点,
∴.
故答案为:4.
三、解答题
19.
解:因为EG平分,FG平分(已知),
所以,(角平分线的定义),
所以(等式的性质).
又因为(已知),
所以,
所以(同旁内角互补,两直线平行).
20.60°
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.
解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED-∠B=85°-50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°-∠B-∠BAC=180°-50°-70°=60°.
三、解答题
21.
解:∵AD平分∠BAC交BC于点D,
∴∠BAD=∠EAD,
∵DE∥AB,
∴∠BAD=∠ADE,
∴∠EAD=∠ADE,
∴AE=DE.
22.
(1)解:如图,过点A作AE⊥BC,
则,
∵AE=AE,
∴.
(2)解:∵和是等高三角形,
∴,
∴;
∵和是等高三角形,
∴,
∴.
(3)解:∵和是等高三角形,
∴,
∴;
∵和是等高三角形,
∴,
∴.
23.
解:(1)中,∵,,,
∴的周长,
∴当把的周长分成相等的两部分时,点P在上,此时,
∴,
解得.
故答案为:6;
(2)当点P在中点时,把的面积分成相等的两部分,此时,
∴,
解得.
故答案为:6.5;
(3)分两种情况:
①当P在上时,
∵的面积=12,
∴,
∴,
∴,;
②当P在上时,
∵的面积=12=面积的一半,
∴P为中点,
∴,.
故t为2或6.5秒时,的面积为12.
24.
解:(1)∵BC=7,AC=8,AB=9,
∴
答:△ABC面积是;
(2)如图,过点I作IF⊥AB、IG⊥AC、IH⊥BC,垂足分别为点F、G、H,
∵AD、BE分别为△ABC的角平分线,
∴IF=IH=IG,
∵S△ABC=S△ABI+S△ACI+S△BCI,
∴(9 IF+8 IF+7 IF)=
解得IF=
故S△ABI=AB FI=×9×=.
