人教版八年级数学上册试题 第十一章《三角形》单元测试卷(含解析)
文档属性
| 名称 | 人教版八年级数学上册试题 第十一章《三角形》单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 559.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 18:59:47 | ||
图片预览



文档简介
第十一章《三角形》单元测试卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形具有稳定性的是( )
A. B. C. D.
2.以下列各组线段为边,能组成三角形的是( )
A. B.
C. D.
3.图中的三角形被木板遮住了一部分,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
4.下列四个图中,正确画出中边上的高是( )
A. B. C. D.
5.直角三角形一个锐角是30度,另一个锐角的度数是( )
A.60度 B.30度 C.90度 D.45度
6.如图,中,,沿着图中的折叠,点刚好落在边上的点处,则的度数是( )
A. B. C. D.
7.如图,将一副直角三角板按如图所示的方式放置,与交于点E,则的度数为( )
A. B. C. D.
8.一个n边形从一个顶点可引3条对角线,则n为( )
A.6 B.5 C.4 D.3
9.小明家住黄山市,小明的爸爸刚在市区买了一套住房,带着小明去选地砖准备装修,看着满目美丽的正三角形,正方形、正六边形、正八边形地砖,不知道选哪种好,但是爸爸告诉小明:有一种地砖是不能单独铺满地面的,必须与另外一种形状的地砖混合使用,让小明指出这种地砖,小明略加思考便选出来了,小明选择的地砖的形状是( )
A.正三角形 B.正方形 C.正八边形 D.正六边形
10.如图,将五边形沿对角线所在的直线剪开,得到四边形和,设四边形内角和为,三角形内角和为,则与的关系式( )
A. B. C. D.无法确定
二、填空题(本大题共8小题,每小题4分,共32分)
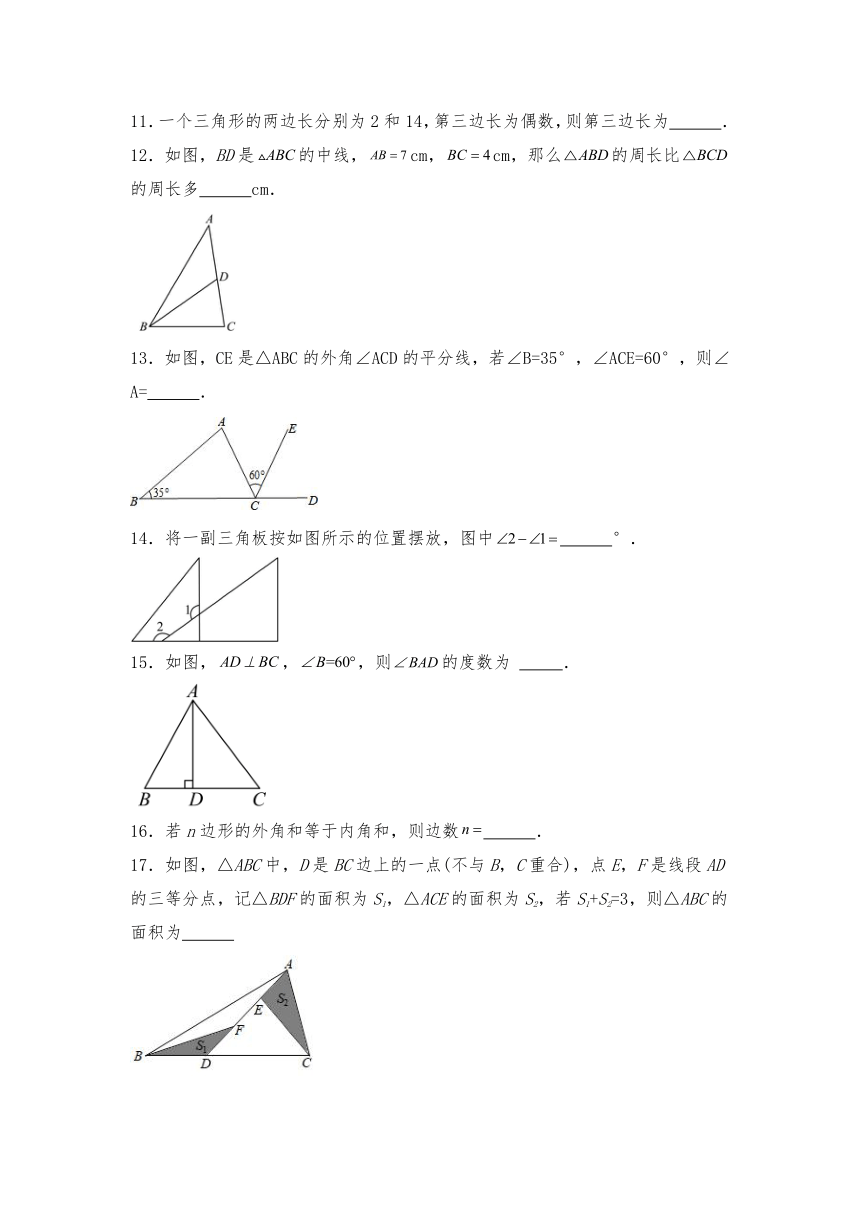
11.一个三角形的两边长分别为2和14,第三边长为偶数,则第三边长为 .
12.如图,BD是的中线,cm,cm,那么的周长比的周长多 cm.
13.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A= .
14.将一副三角板按如图所示的位置摆放,图中 °.
15.如图,,,则的度数为 .
16.若n边形的外角和等于内角和,则边数 .
17.如图,△ABC中,D是BC边上的一点(不与B,C重合),点E,F是线段AD的三等分点,记△BDF的面积为S1,△ACE的面积为S2,若S1+S2=3,则△ABC的面积为
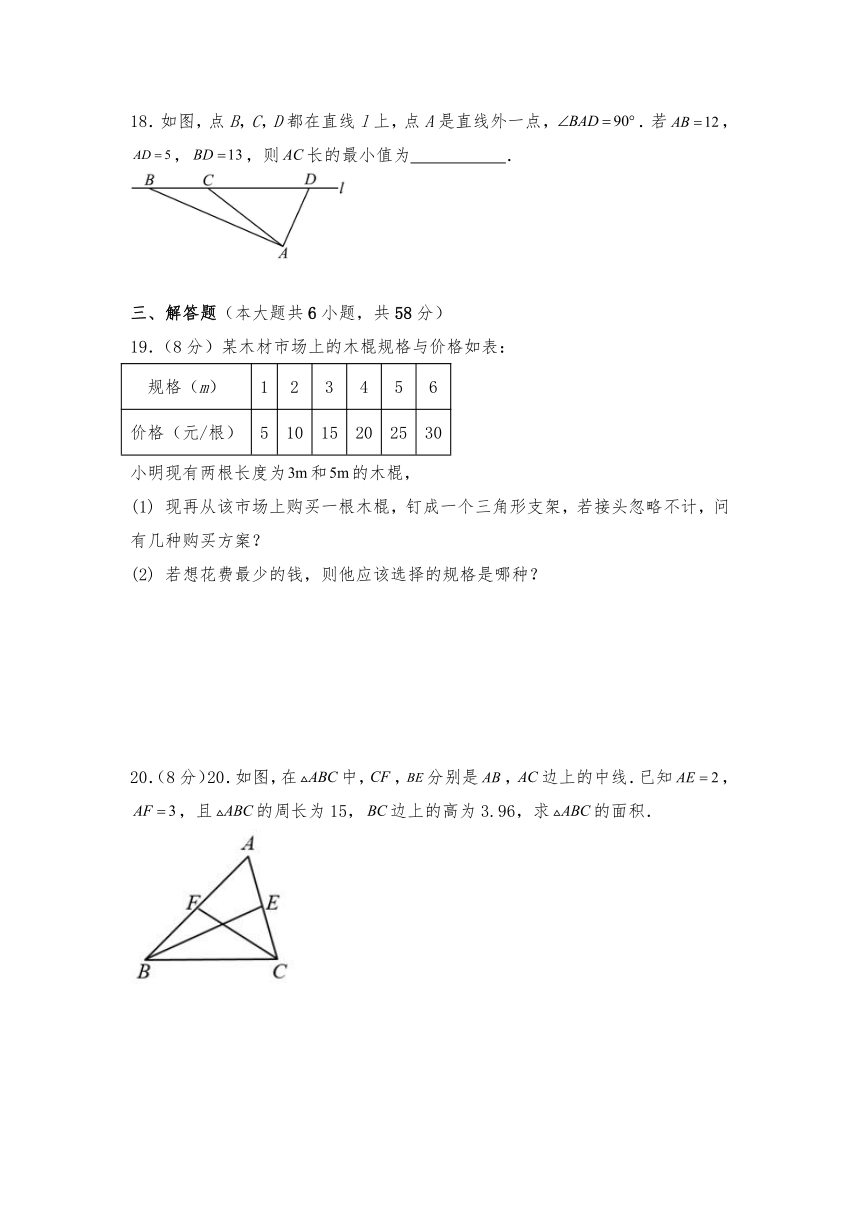
18.如图,点B,C,D都在直线l上,点A是直线外一点,.若,,,则长的最小值为 .
三、解答题(本大题共6小题,共58分)
19.(8分)某木材市场上的木棍规格与价格如表:
规格(m) 1 2 3 4 5 6
价格(元/根) 5 10 15 20 25 30
小明现有两根长度为和的木棍,
现再从该市场上购买一根木棍,钉成一个三角形支架,若接头忽略不计,问有几种购买方案?
若想花费最少的钱,则他应该选择的规格是哪种?
20.(8分)20.如图,在中,,分别是,边上的中线.已知,,且的周长为15,边上的高为3.96,求的面积.
21.(10分)如图所示,的两边上各有一点,连接,求证.
22.(10分)如图,在中,于D,平分交于点E,,求的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:( ),
(等式的性质).
∵平分(已知),
∴ ( ).
∵(已知),
∴
∵
∴ = .
23.(10分)在中,点是延长线上一点.
(1)如图1,过点作,交于点,.
①若,则______°;
②试写出与的数量关系,并说明理由;
③当时,求的度数;
④若,请说明;
(2)如图2,交于点,,直接写出、与之间的数量关系.
24.(12分)在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.三角形的内角和是180 ,那么,四边形的内角和是多少度呢?如图,作四边形的对角线,它把四边形分成两个三角形,四边形的四个角的和就是这两个三角形的内角的和,因此,四边形的内角和等于.
过五边形一个顶点的对角线,可以把五边形分成几个三角形?它的内角和是多少度?
对于六边形呢?七边形呢?……过n边形一个顶点的所有对角线,可以把n边形分成多少个三角形?n边形的内角和是多少度?
答案
一、单选题
1.D
【分析】根据三角形具有稳定性解答.
【详解】解:选项中只有选项D是三角形组成,故具有稳定性.
故选:D.
2.D
【分析】根据三角形三边关系:较短边的和大于较长边的长度即可解答.
【详解】解:∵,
∴较短边的和等于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和小于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和等于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和大于较长边的边长,
∴此三角形存在,
故项符合题意;
故选.
3.D
【分析】根据图中信息即可判定.
【详解】解:图中被木板遮住的三角形有可能是锐角三角形、直角三角形、钝角三角形,
故选:D.
4.C
【分析】从三角形一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫做三角形的高,根据三角形的高的定义逐一判断,即可得到答案.
【详解】解:根据三角形高线的定义,边上的高是过点A向作垂线,垂足为D,
纵观各图形,选项A、B、D都不符合题意,只有选项C符合题意,
故选:C.
5.A
【分析】直接根据直角三角形两锐角互余即可解答.
【详解】解:直角三角形一个锐角是30度,另一个锐角的度数是.
故选A.
6.C
【分析】由折叠的性质可求得∠ACD=∠BCD,∠BDC=∠CDE,在△ACD中,利用外角可求得∠BDC,则可求得答案.
【详解】解:由折叠可得∠ACD=∠BCD,∠BDC=∠CDE,
∵∠ACB=90°,
∴∠ACD=45°,
∵∠A=30°,
∴∠BDC=∠A+∠ACD=30°+45°=75°,
∴∠CDE=75°.
故选C.
7.C
【分析】根据三角形的外角性质即可得.
【详解】解:由题意得:,
,
故选:C.
8.A
【分析】可根据n边形从一个顶点引出的对角线与边的关系:,列方程求解.
【详解】解:设多边形有n条边,
则,
解得,.
故选:A.
9.C
【分析】根据正多边形的镶嵌应符合一个内角能整除进行判断即可.
【详解】解:A、正三角形的每个内角是,能整除,能密铺,故A不符合题意;
B、正方形的每个内角是,4个能密铺,故B不符合题意;
C、正八边形每个内角是,不能整除,不能密铺,故C符合题意;
D、正六边形的每个内角是,能整除,能密铺,故D不符合题意.
故选C.
10.A
【分析】根据三角形内角和公式与三角形内角和定理即可求解.
【详解】解:依题意,,
∴,
故选:A.
二、填空题
11.14
【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;又知道第三边长为偶数,就可以知道第三边的长度.
【详解】解:设第三边长为,根据三角形的三边关系,得
,
即.
又∵第三边长是偶数,则,
故答案为:14.
12.3
【分析】根据三角形的中线的概念得到,根据三角形的周长公式计算,得到答案.
【详解】解:∵BD是的中线,
∴,
∴的周长的周长
(cm),
∴的周长比的周长多3cm,
故答案为:3.
13.
【分析】根据角平分线的性质,可知∠ACD,进而根据三角形外角定理,即可求得∠A.
【详解】∵CE是角∠ACD的平分线,∠ACE=60°
∴∠ACD=120°
又∵∠ACD是△ABC的外角
∴∠A=∠ACD-∠B=85°
故答案为85°.
14.30
【分析】先求解,再进行计算即可.
【详解】解:如图,标注三角形的顶点,
∵,
∴,
∵,
∴,
∴,
故答案为:
15.
【分析】根据垂线定义得出,根据直角三角形两锐角互余,结合,求出结果即可.
【详解】解:∵,
∴,
∵,
∴.
故答案为:.
16.4
【分析】根据边形的内角和可以表示成,外角和为,根据题意列方程求解.
【详解】解:由题意得,
解得:.
故答案为:4.
17.9
【分析】根据点E,F是线段AD的三等分点,可得到S△ABD=3S1,S△ADC=3S2,代入即可求出△ABC的面积.
【详解】解:∵点E,F是线段AD的三等分点,
∴DF=AE=AD,
∴S△ABD=3S1,
同理可知:S△ADC=3S2,
∴S△ABC=S△ABD+S△ADC
=3S1+3S2
=3(S1+S2)
=3×3
=9.
故答案为:9.
18.
【分析】根据垂线段最短,可知当时,最短,再根据面积相等即可得出答案.
【详解】解:根据垂线段最短,可知当时,最短,
∵,,,,
∴,即,
∴,
故答案为:.
三、解答题
19.(1)解:设第三根木棒的长度为,
根据三角形的三边关系可得:,
解得,
,4,5,6,共4种,
一共有四种方案.
(2)解:∵规格为的木棍价格最低,
∴应该选择的规格是.
20.解:∵,分别是,边上的中线,,,
∴,
.
∵的周长为15,
∴,
∴.
21.解:和是的外角,
.
又,
.
22.解:(三角形内角和定理),
(等式的性质),
∵平分(已知),
∴(角平分线的定义),
∵(已知),
∵
故答案为:三角形内角和定理,角平分线的定义
23.(1)①∵,
∴.
故答案为:.
②.
理由如下:
∵,
∴
.
即.
③∵,,
∴.
∴.
∴.
④∵,,
∴.
∴.
∴.
(2).理由如下:
如图,延长至.
∵,,,
∴.
24.(1)解:过五边形一个顶点的对角线,可以把五边形分成3个三角形,因为每个三角形的内角和为,故五边形的内角和为.
(2)解:过六边形一个顶点的对角线,可以把五边形分成4个三角形,因为每个三角形的内角和为,故五边形的内角和为.
过七边形一个顶点的对角线,可以把七边形分成5个三角形,因为每个三角形的内角和为180°,故五边形的内角和为.
……
过n边形一个顶点的对角线,可以把n边形分成个三角形,因为每个三角形的内角和为180°,故n边形的内角和为
一、单选题(本大题共10小题,每小题3分,共30分)
1.下列图形具有稳定性的是( )
A. B. C. D.
2.以下列各组线段为边,能组成三角形的是( )
A. B.
C. D.
3.图中的三角形被木板遮住了一部分,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
4.下列四个图中,正确画出中边上的高是( )
A. B. C. D.
5.直角三角形一个锐角是30度,另一个锐角的度数是( )
A.60度 B.30度 C.90度 D.45度
6.如图,中,,沿着图中的折叠,点刚好落在边上的点处,则的度数是( )
A. B. C. D.
7.如图,将一副直角三角板按如图所示的方式放置,与交于点E,则的度数为( )
A. B. C. D.
8.一个n边形从一个顶点可引3条对角线,则n为( )
A.6 B.5 C.4 D.3
9.小明家住黄山市,小明的爸爸刚在市区买了一套住房,带着小明去选地砖准备装修,看着满目美丽的正三角形,正方形、正六边形、正八边形地砖,不知道选哪种好,但是爸爸告诉小明:有一种地砖是不能单独铺满地面的,必须与另外一种形状的地砖混合使用,让小明指出这种地砖,小明略加思考便选出来了,小明选择的地砖的形状是( )
A.正三角形 B.正方形 C.正八边形 D.正六边形
10.如图,将五边形沿对角线所在的直线剪开,得到四边形和,设四边形内角和为,三角形内角和为,则与的关系式( )
A. B. C. D.无法确定
二、填空题(本大题共8小题,每小题4分,共32分)
11.一个三角形的两边长分别为2和14,第三边长为偶数,则第三边长为 .
12.如图,BD是的中线,cm,cm,那么的周长比的周长多 cm.
13.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A= .
14.将一副三角板按如图所示的位置摆放,图中 °.
15.如图,,,则的度数为 .
16.若n边形的外角和等于内角和,则边数 .
17.如图,△ABC中,D是BC边上的一点(不与B,C重合),点E,F是线段AD的三等分点,记△BDF的面积为S1,△ACE的面积为S2,若S1+S2=3,则△ABC的面积为
18.如图,点B,C,D都在直线l上,点A是直线外一点,.若,,,则长的最小值为 .
三、解答题(本大题共6小题,共58分)
19.(8分)某木材市场上的木棍规格与价格如表:
规格(m) 1 2 3 4 5 6
价格(元/根) 5 10 15 20 25 30
小明现有两根长度为和的木棍,
现再从该市场上购买一根木棍,钉成一个三角形支架,若接头忽略不计,问有几种购买方案?
若想花费最少的钱,则他应该选择的规格是哪种?
20.(8分)20.如图,在中,,分别是,边上的中线.已知,,且的周长为15,边上的高为3.96,求的面积.
21.(10分)如图所示,的两边上各有一点,连接,求证.
22.(10分)如图,在中,于D,平分交于点E,,求的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:( ),
(等式的性质).
∵平分(已知),
∴ ( ).
∵(已知),
∴
∵
∴ = .
23.(10分)在中,点是延长线上一点.
(1)如图1,过点作,交于点,.
①若,则______°;
②试写出与的数量关系,并说明理由;
③当时,求的度数;
④若,请说明;
(2)如图2,交于点,,直接写出、与之间的数量关系.
24.(12分)在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.三角形的内角和是180 ,那么,四边形的内角和是多少度呢?如图,作四边形的对角线,它把四边形分成两个三角形,四边形的四个角的和就是这两个三角形的内角的和,因此,四边形的内角和等于.
过五边形一个顶点的对角线,可以把五边形分成几个三角形?它的内角和是多少度?
对于六边形呢?七边形呢?……过n边形一个顶点的所有对角线,可以把n边形分成多少个三角形?n边形的内角和是多少度?
答案
一、单选题
1.D
【分析】根据三角形具有稳定性解答.
【详解】解:选项中只有选项D是三角形组成,故具有稳定性.
故选:D.
2.D
【分析】根据三角形三边关系:较短边的和大于较长边的长度即可解答.
【详解】解:∵,
∴较短边的和等于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和小于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和等于较长边的边长,
∴此三角形不存在,
故项不符合题意;
∵,
∴较短边的和大于较长边的边长,
∴此三角形存在,
故项符合题意;
故选.
3.D
【分析】根据图中信息即可判定.
【详解】解:图中被木板遮住的三角形有可能是锐角三角形、直角三角形、钝角三角形,
故选:D.
4.C
【分析】从三角形一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫做三角形的高,根据三角形的高的定义逐一判断,即可得到答案.
【详解】解:根据三角形高线的定义,边上的高是过点A向作垂线,垂足为D,
纵观各图形,选项A、B、D都不符合题意,只有选项C符合题意,
故选:C.
5.A
【分析】直接根据直角三角形两锐角互余即可解答.
【详解】解:直角三角形一个锐角是30度,另一个锐角的度数是.
故选A.
6.C
【分析】由折叠的性质可求得∠ACD=∠BCD,∠BDC=∠CDE,在△ACD中,利用外角可求得∠BDC,则可求得答案.
【详解】解:由折叠可得∠ACD=∠BCD,∠BDC=∠CDE,
∵∠ACB=90°,
∴∠ACD=45°,
∵∠A=30°,
∴∠BDC=∠A+∠ACD=30°+45°=75°,
∴∠CDE=75°.
故选C.
7.C
【分析】根据三角形的外角性质即可得.
【详解】解:由题意得:,
,
故选:C.
8.A
【分析】可根据n边形从一个顶点引出的对角线与边的关系:,列方程求解.
【详解】解:设多边形有n条边,
则,
解得,.
故选:A.
9.C
【分析】根据正多边形的镶嵌应符合一个内角能整除进行判断即可.
【详解】解:A、正三角形的每个内角是,能整除,能密铺,故A不符合题意;
B、正方形的每个内角是,4个能密铺,故B不符合题意;
C、正八边形每个内角是,不能整除,不能密铺,故C符合题意;
D、正六边形的每个内角是,能整除,能密铺,故D不符合题意.
故选C.
10.A
【分析】根据三角形内角和公式与三角形内角和定理即可求解.
【详解】解:依题意,,
∴,
故选:A.
二、填空题
11.14
【分析】已知两边,则第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围;又知道第三边长为偶数,就可以知道第三边的长度.
【详解】解:设第三边长为,根据三角形的三边关系,得
,
即.
又∵第三边长是偶数,则,
故答案为:14.
12.3
【分析】根据三角形的中线的概念得到,根据三角形的周长公式计算,得到答案.
【详解】解:∵BD是的中线,
∴,
∴的周长的周长
(cm),
∴的周长比的周长多3cm,
故答案为:3.
13.
【分析】根据角平分线的性质,可知∠ACD,进而根据三角形外角定理,即可求得∠A.
【详解】∵CE是角∠ACD的平分线,∠ACE=60°
∴∠ACD=120°
又∵∠ACD是△ABC的外角
∴∠A=∠ACD-∠B=85°
故答案为85°.
14.30
【分析】先求解,再进行计算即可.
【详解】解:如图,标注三角形的顶点,
∵,
∴,
∵,
∴,
∴,
故答案为:
15.
【分析】根据垂线定义得出,根据直角三角形两锐角互余,结合,求出结果即可.
【详解】解:∵,
∴,
∵,
∴.
故答案为:.
16.4
【分析】根据边形的内角和可以表示成,外角和为,根据题意列方程求解.
【详解】解:由题意得,
解得:.
故答案为:4.
17.9
【分析】根据点E,F是线段AD的三等分点,可得到S△ABD=3S1,S△ADC=3S2,代入即可求出△ABC的面积.
【详解】解:∵点E,F是线段AD的三等分点,
∴DF=AE=AD,
∴S△ABD=3S1,
同理可知:S△ADC=3S2,
∴S△ABC=S△ABD+S△ADC
=3S1+3S2
=3(S1+S2)
=3×3
=9.
故答案为:9.
18.
【分析】根据垂线段最短,可知当时,最短,再根据面积相等即可得出答案.
【详解】解:根据垂线段最短,可知当时,最短,
∵,,,,
∴,即,
∴,
故答案为:.
三、解答题
19.(1)解:设第三根木棒的长度为,
根据三角形的三边关系可得:,
解得,
,4,5,6,共4种,
一共有四种方案.
(2)解:∵规格为的木棍价格最低,
∴应该选择的规格是.
20.解:∵,分别是,边上的中线,,,
∴,
.
∵的周长为15,
∴,
∴.
21.解:和是的外角,
.
又,
.
22.解:(三角形内角和定理),
(等式的性质),
∵平分(已知),
∴(角平分线的定义),
∵(已知),
∵
故答案为:三角形内角和定理,角平分线的定义
23.(1)①∵,
∴.
故答案为:.
②.
理由如下:
∵,
∴
.
即.
③∵,,
∴.
∴.
∴.
④∵,,
∴.
∴.
∴.
(2).理由如下:
如图,延长至.
∵,,,
∴.
24.(1)解:过五边形一个顶点的对角线,可以把五边形分成3个三角形,因为每个三角形的内角和为,故五边形的内角和为.
(2)解:过六边形一个顶点的对角线,可以把五边形分成4个三角形,因为每个三角形的内角和为,故五边形的内角和为.
过七边形一个顶点的对角线,可以把七边形分成5个三角形,因为每个三角形的内角和为180°,故五边形的内角和为.
……
过n边形一个顶点的对角线,可以把n边形分成个三角形,因为每个三角形的内角和为180°,故n边形的内角和为
