(备战期末)专题04:圆-2023-2024学年数学五年级下册苏教版(含答案)
文档属性
| 名称 | (备战期末)专题04:圆-2023-2024学年数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 718.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 11:41:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
(备战期末)专题04:圆-2023-2024学年数学五年级下册苏教版
一、选择题
1.小明在游乐场骑玩具车,在平直的轨道上,车有规律的上下起伏。下面说法,错误的是( )。
A.车轮不是圆形的 B.车轴没有装在圆形车轮的圆心处
C.A、B都有可能 D.车把松动了
2.美术老师用彩色卡纸制作了一个2022年冬奥会吉祥物“冰墩墩”,制作时需要把一个直径4厘米的圆形纸片剪成两个半圆,这两个半圆的周长和是( )厘米。
A.10.28 B.12.56 C.16.56 D.20.56
3.如图,大圆01的半径是5厘米,小圆02的半径是2厘米。如小圆02围绕大圆01的圆周滚动一周,小圆O2的圆心移动了( )厘米。
A.14π B.21π C.24π D.49π
4.从3块边长都是12厘米的正方形铁皮中,分别剪去如下图所示的黑色部分,剩下的铁皮面积( )。
A.①大 B.②大 C.③大 D.一样大
5.下面关于圆周率的说法,错误的是( )。
A.是圆的周长与它的直径的比值
B.大圆和小圆相比,大圆的的值要大一些
C.3.14是的一个近似值
D.是一个无限不循环小数
6.李明去披萨店点了一个12寸的披萨,过了一会服务员过来说:“不好意思,现在做不了12寸的,您看换成2个6寸的可以吗?反正一样大!”你认为呢?(说明:12寸、6寸,是指披萨的直径)( )。
A.12寸的大 B.2个6寸的大 C.一样大 D.无法确定
二、填空题
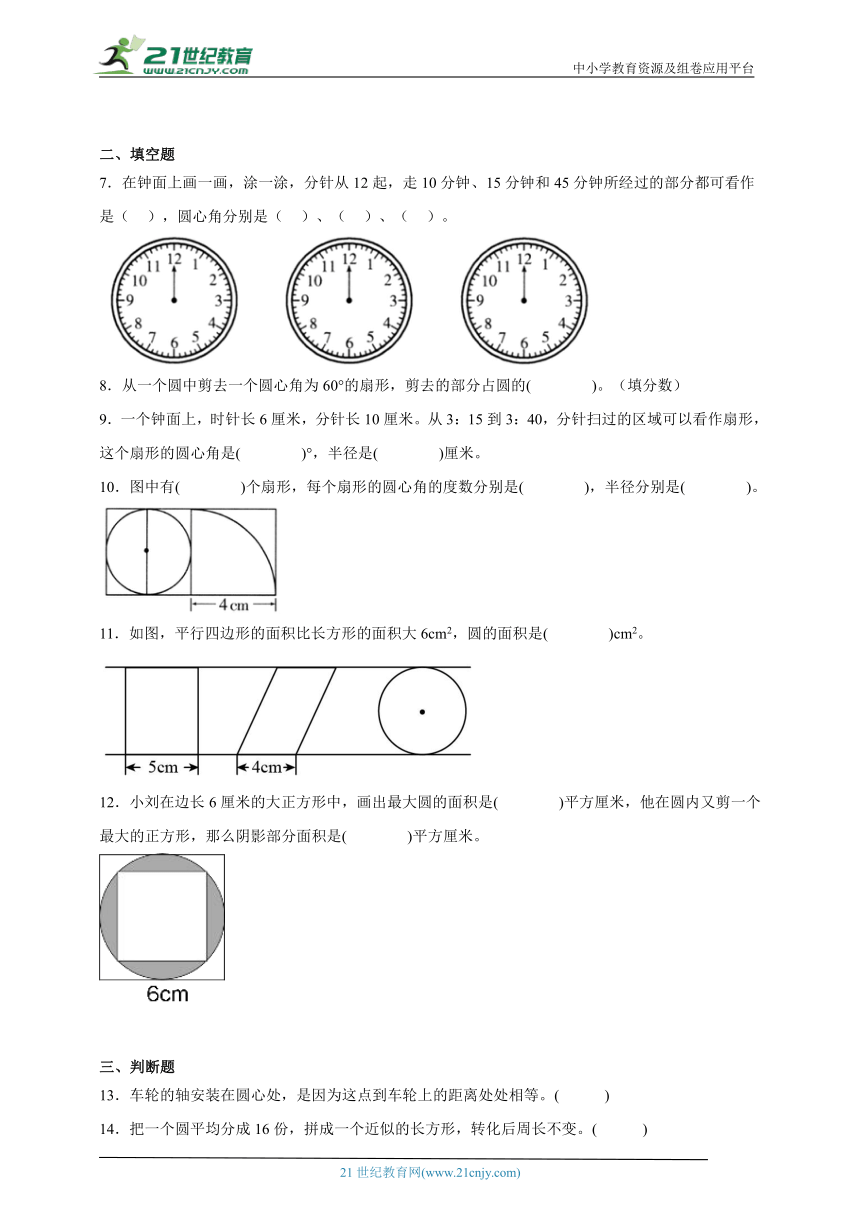
7.在钟面上画一画,涂一涂,分针从12起,走10分钟、15分钟和45分钟所经过的部分都可看作是( ),圆心角分别是( )、( )、( )。
8.从一个圆中剪去一个圆心角为60°的扇形,剪去的部分占圆的( )。(填分数)
9.一个钟面上,时针长6厘米,分针长10厘米。从3:15到3:40,分针扫过的区域可以看作扇形,这个扇形的圆心角是( )°,半径是( )厘米。
10.图中有( )个扇形,每个扇形的圆心角的度数分别是( ),半径分别是( )。
11.如图,平行四边形的面积比长方形的面积大6cm2,圆的面积是( )cm2。
12.小刘在边长6厘米的大正方形中,画出最大圆的面积是( )平方厘米,他在圆内又剪一个最大的正方形,那么阴影部分面积是( )平方厘米。
三、判断题
13.车轮的轴安装在圆心处,是因为这点到车轮上的距离处处相等。( )
14.把一个圆平均分成16份,拼成一个近似的长方形,转化后周长不变。( )
15.在长6厘米、宽4厘米的长方形里画一个最大的半圆,半圆的半径是3厘米。( )
16.圆心角是60度的扇形的面积是它所在圆的面积的。( )
17.直径是6分米的圆比半径是4分米的圆要大一些。( )
四、计算题
18.计算下图中阴影部分的面积。
19.求涂色部分的面积。
五、解答题
20.幸福小区有一个圆形花坛,量得花坛一周的篱笆长是25.12米。这个花坛的占地面积是多少平方米?
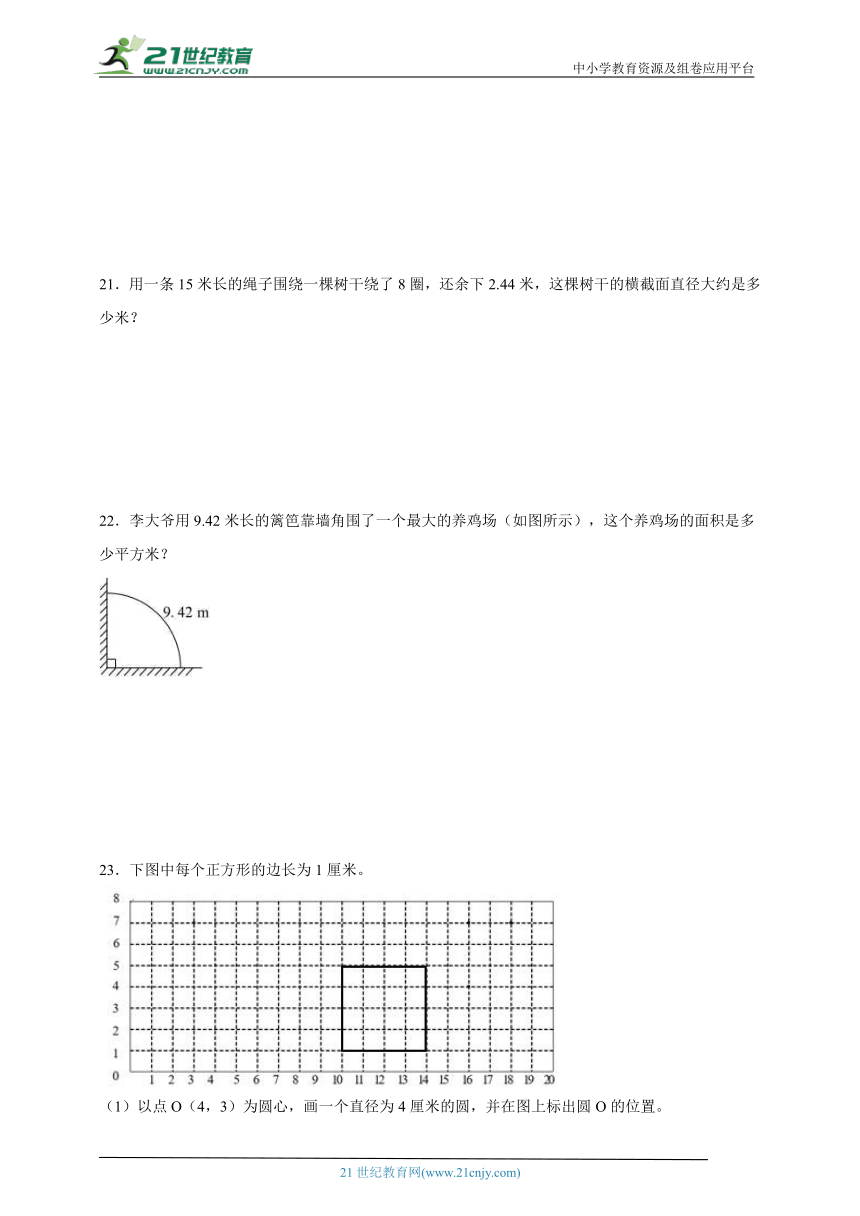
21.用一条15米长的绳子围绕一棵树干绕了8圈,还余下2.44米,这棵树干的横截面直径大约是多少米?
22.李大爷用9.42米长的篱笆靠墙角围了一个最大的养鸡场(如图所示),这个养鸡场的面积是多少平方米?
23.下图中每个正方形的边长为1厘米。
(1)以点O(4,3)为圆心,画一个直径为4厘米的圆,并在图上标出圆O的位置。
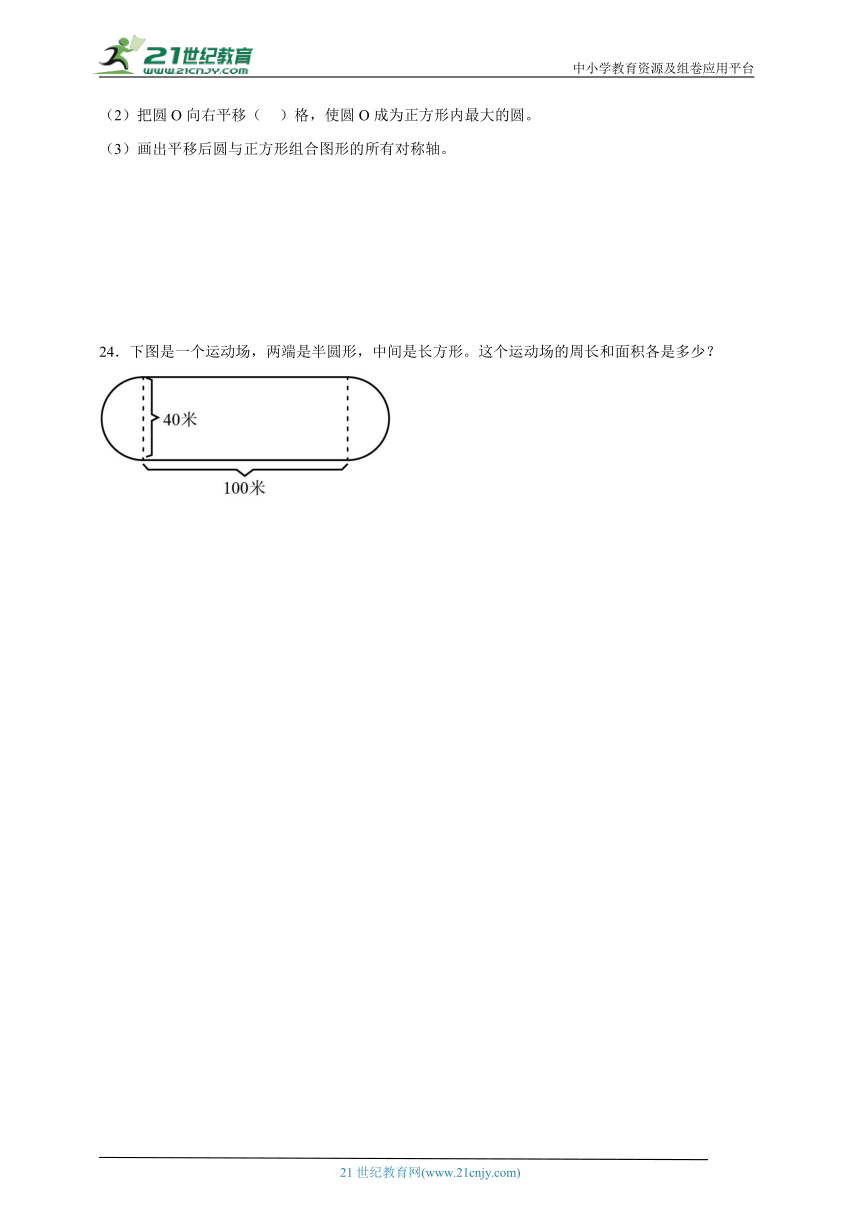
(2)把圆O向右平移( )格,使圆O成为正方形内最大的圆。
(3)画出平移后圆与正方形组合图形的所有对称轴。
24.下图是一个运动场,两端是半圆形,中间是长方形。这个运动场的周长和面积各是多少?
参考答案:
1.D
【分析】根据圆的特征,逐项分析,进行解答即可。
【详解】根据在平直的轨道上,车有规律的上下起伏分析如下:
A.车轮不是圆形的,有可能造成有规律的上下起伏,原题干说法正确;
B.车轴没有装在圆形车轮的圆心处,有可能造成车有规律的上下起伏,原题干说法正确;
C.车轮不是圆形的,车轴没有装在圆形车轮的圆心处,都有可能造成车有规律的上下起伏,原题干说法正确;
D.车把松动一般不会造成车有规律的上下起伏,原题干说法错误。
小明在游乐场骑玩具车,在平直的轨道上,车有规律的上下起伏。下面说法,错误的车把松动了。
故答案为:D
【点睛】本题考查圆的特征的知识,结合题意分析解答即可。
2.D
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径,所以这两个半圆的周长和比圆的周长增加两条直径的长度,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
故答案为:D
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的公式及应用。
3.A
【分析】通过观察图形可知,小圆O2围绕大圆O1的圆周滚动一周,小圆O2的圆心移动的距离等于半径为(5+2)厘米的圆的周长,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】π×(5+2)×2
=π×7×2
=14π(厘米)
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
4.D
【分析】由题意可知:
图①:剩下的铁皮面积=正方形的面积-一个大圆的面积;
图②:剩下的铁皮面积=正方形的面积-9个小圆的面积;
图③:剩下的铁皮面积=正方形的面积-4个小扇形的面积(每个小扇形相当于圆的面积,4个小扇形就相当于一个圆的面积);
【详解】正方形的面积:12×12=144(平方厘米)
图①:圆的半径12÷2=6(厘米)
剩下的铁皮面积:
144-3.14×
=144-113.04
=30.96(平方厘米)
图②:圆的半径
12÷3÷2
=4÷2
=2(厘米)
剩下的铁皮面积:
144-3.14××9
=144-12.56×9
=144-113.04
=30.96(平方厘米)
图③:圆的半径12÷2=6(厘米)
剩下的铁皮面积:
144-3.14×
=144-113.04
=30.96(平方厘米)
图①剩余面积=图②剩余面积=图③剩余面积
故答案为:D
【点睛】解答此题的关键是明白:剩下的铁皮的面积=正方形的面积-圆的面积,只要补充上直径的长度,即可求解。
5.B
【分析】根据圆周率的意义:圆的周长和它的直径的比值,叫做圆周率;用字母π表示;π是一个无限不循环的小数,据此解答。
【详解】A.根据圆周率的意义可知,π是圆的周长与它的直径的比值;原题干说法正确;
B.圆的大小与圆周率无关,圆周率不会随着圆的大小的改变而改变;原题干说法错误;
C.3.14是π的一个近似值,原题干说法正确;
D.π是一个无限不循环小数,原题干说法正确。
故答案为:B
【点睛】根据圆周率的意义进行解答。
6.A
【分析】因为披萨厚度一样,所以只要比较12寸的和两个6寸的底面积的大小即可,根据圆的公式S=πr2,把具体数据代入计算即可。
【详解】12寸披萨的面积:
3.14×(12÷2)2
=3.14×36
=113.04(平方英寸)
2个6寸披萨的面积:
3.14×(6÷2)2×2
=3.14×9×2
=56.52(平方英寸)
因为113.04平方英寸>56.52平方英寸,所以12寸披萨的面积大。
故答案为:A
【点睛】此题主要考查圆面积公式的灵活运用及小数大小的比较。
7.扇形;60°、90°、270°
【分析】根据扇形的定义是一条弧和经过这条弧两端的两条半径所围成的图形,由此结合题意即可得出答案;钟面分成12个大格,分针每过一个大格是5分钟;分针指向3,走10分钟、15分钟和45分钟分别走了10÷5=2个大格,15÷5=3个大格,45÷5=9个大格;根据钟表的认识,角的分类,钟面上的分针从12起走一圈走了60分钟;走过的角是周角;是360度;钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,依此解答。
【详解】根据扇形的定义,可得分针从12起,走10分钟、15分钟和45分钟所经过的部分都可看作是扇形。
如图:
10÷5=2
15÷5=3
45÷5=9
2×30°=60°
3×30°=90°
9×30°=270°
圆心角分别是60°、90°、270°。
【点睛】本题考查了认识平面图形的知识,属于基础题,解题关键是要求指向旋转了多少度,关键是看走了几个数字。
8.
【分析】周角是360°,用60°除以360°即可表示剪去部分占圆的几分之几。
【详解】60÷360=
即剪去的部分占圆的。
【点睛】此题解答关键是明确:周角是360°,根据求一个数是另一个数的几分之几,用除法解答。
9. 150 10
【分析】钟面上一个大格是5分钟,是30°,从3:15到3:40,是25分钟,25÷5=5,走过来5个大格,再用一个大格的度数×5,即可求出这个扇形的圆心角的度数,因为是分针扫过的区域,所以扇形的半径等于分针的长度,据此解答。
【详解】3:15到3:40,是25分钟。
30°×(25÷5)
=30°×5
=150°
一个钟面上,时针长6厘米,分针长10厘米。从3:15到3:40,分针扫过的区域可以看作扇形,这个扇形的圆心角是150°,半径是10厘米。
【点睛】本题主要考查钟表时间与扇形圆心角的关系,关键是求出分针从3:15到3:40,走过的时间。
10. 3 180°、180°、90° 2厘米、2厘米、4厘米
【分析】根据扇形的意义:一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形(半圆和直径的组合也是扇形),它是由圆周的一部分与它所对应的圆心角围成,据此解答。
【详解】4÷2=2(厘米)
图中有3个扇形,左边图有2个扇形,右边图有1个扇形;左边2个扇形的圆心角是180度,右边扇形的圆心角是90°;左边扇形半径是2厘米,右边扇形半径是4厘米。
【点睛】熟练掌握扇形的特征是解答本题的关键。
11.28.26
【分析】长方形的长、平行四边形的高、圆的直径相等。由平行四边形的面积比长方形的面积大6 cm2,可知平行四边形的高是6÷(5-4)=6(cm),所以圆的半径是:6÷2=3(cm);再根据圆的面积公式:,即可求出圆的面积。
【详解】6÷(5-4)
=6÷1
=6(cm)
6÷2=3(cm)
3.14×32
=3.14×9
=28.26(cm2)
所以,圆的面积是28.26cm2。
【点睛】正确理解图意,熟记长方形、平行四边形、圆的面积计算公式,是解答此题的关键。
12. 28.26 10.26
【分析】观察图形可知,大正方形中最大圆的直径等于正方形的边长,是6厘米,则半径是6÷2=3(厘米),根据圆的面积=πr2即可求出这个圆的面积。
如下图所示,把圆中最大的正方形平均分成2个完全相同的三角形,三角形的一条底等于圆的直径,对应的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2求出圆内最大正方形的面积。最后用圆的面积减去这个正方形的面积即可求出阴影部分的面积。
【详解】6÷2=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
28.26-6×3÷2×2
=28.26-18
=10.26(平方厘米)
则画出最大圆的面积是28.26平方厘米,阴影部分面积是10.26平方厘米。
【点睛】本题考查了圆和三角形面积的运算。把圆内最大正方形的面积转化为两个三角形的面积进行计算是解题的关键。
13.√
【分析】根据半径的定义:连接圆心和圆上任意一点的线段,叫做半径;同一个圆里,有无数条半径,所有半径长度都相等。以此判断。
【详解】车轮的轴安装在圆心处,从圆心到车轮上的距离就是圆的半径,因为所有的半径长度都相等,所以这点到车轮上的距离处处相等。
故答案为:√
【点睛】此题主要考查了圆的特征,同一个圆内,所有的半径都相等。
14.×
【分析】根据圆拼成的长方形的过程可知,近似长方形的长等于圆周长()的一半,宽等于圆的半径,然后根据长方形的周长计算列式与圆的周长公式进行比对,据此解答。
【详解】长:πr,宽:r;
长方形周长=(长+宽)×2=(πr+r)×2=2πr+2r
因为圆的周长=2πr,所以周长发生了改变。
所以原题说法错误。
【点睛】此题主要考查了学生对圆进行切割拼组后的长方形的周长变化规律的了解与实际推算。
15.√
【分析】根据题意可知,在一个长方形里画一个最大的半圆,半圆的直径等于长方形的长,以此解答。
【详解】由于在一个长方形里画一个最大的半圆,半圆的直径等于长方形的长,那么半圆的半径就等于6÷2=3(厘米)
所以原题说法正确。
【点睛】此题关键在于理解长方形内最大的半圆的直径等于长方形的长。
16.√
【分析】扇形的面积=扇形所在圆的面积× 据此判断即可。
【详解】60÷360=,所以圆心角是60度的扇形的面积是它所在圆的面积的。原题说法正确。
【点睛】此题考查有关扇形的面积计算,掌握扇形面积计算公式是解题关键。
17.×
【分析】分别计算直径是6分米的圆和半径是4分米的圆的面积,比较大小。
【详解】直径是6分米的圆:3.14×(6÷2)2=28.26(平方分米)
半径是4分米的圆:3.14×42=50.24(平方分米);50.24>28.26
直径是6分米的圆比半径是4分米的圆要小一些。原题说法错误。
【点睛】两个圆,直径(半径)较大的圆,面积和周长都较大。
18.3.44
【分析】根据对图形的分析,阴影部分面积为正方形面积减去圆的面积,该正方体边长为4,该圆的直径为4。再根据正方形面积公式:正方形面积=边长×边长,圆的半径=直径÷2,圆的面积公式为:S=r2,将数据代入求解即可。
【详解】由分析可得:
圆半径为:4÷2=2
阴影部分面积为:
4×4-3.14×22
=16-3.14×4
=16-12.56
=3.44
19.113.04cm2
【分析】根据题意,涂色部分的面积,即为环形面积,根据环形面积公式:S=π(R2-r2),代入数据求值即可。
【详解】由分析可得:
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(cm2)
20.50.24平方米
【分析】由题意可知:圆形花坛的周长为25.12米,代入圆的周长公式:C=2πr求出半径,再代入圆的面积公式:S=πr2计算即可。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
3.14×42
=3.14×16
=50.24(平方米)
答:这个花坛的占地面积是50.24平方米。
【点睛】本题考查圆的周长、面积公式的灵活运用,牢记公式是解题的关键。
21.0.5米
【分析】用这根绳子的总长度-余下的长度,即15-2.44,求出绕树干绕8圈的长度,再除以8,求出绕树干绕一圈的长度,也就是这个树的周长,再根据圆的周长公式:周长=π×直径,直径=周长÷π,代入数据,即可解答。
【详解】(15-2.44)÷8÷3.14
=12.56÷8÷3.14
=1.57÷3.14
=0.5(米)
答:这棵树干的横截面直径大约是0.5米。
【点睛】解答本题的关键是求出绳子绕树干绕一圈的长度。
22.28.26平方米
【分析】观察图形可知,这个圆平均分成了4份,其中一份的圆的弧长是9.42米,由此可知,用9.42×4,求出这个圆的周长;根据周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出这个圆的面积,再除以4,即可求出这个养鸡场的面积,据此解答。
【详解】9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62÷4
=113.04÷4
=28.26(平方米)
答:这个养鸡场的面积是28.26平方米。
【点睛】解答本题的关键明确这个圆被平均分成了4份,进而利用圆的周长公式和面积公式进行解答。
23.见详解
【分析】(1)要画直径为4厘米的圆,则半径为(4÷2=2)厘米。结合数对知识,第一个数表示列,第二个数表示行,把圆规的两脚分开,定好两脚间距离是2厘米,把有针尖的一只脚固定在一(4,3)上;带有铅笔的那只脚绕点旋转一周即可完成画圆。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。根据平移的特征,把圆O向右平移,使圆O成为正方形内最大的圆。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可;据此画出平移后圆与正方形组合图形的所有对称轴。
【详解】(1)(3)如下图:
(2)把圆O向右平移8格,使圆O成为正方形内最大的圆。
【点睛】此题考查的知识点:数对与位置、平移的特征、对称轴的知识。
24.周长:325.6米;面积:5256平方米
【分析】根据题意可知,长方形的宽等于圆的直径,运动场的周长=圆的周长+(长方形的长×2);根据圆的周长公式:周长=π×直径;代入数据,求出运动场的周长;运动场的面积=圆的面积+长方形的面积,根据圆的面积公式:面积=π×半径2,长方形面积公式:面积=长×宽,代入数据,即可求出运动场面积。
【详解】周长:3.14×40+2×100
=125.6+200
=325.6(米)
面积:3.14×(40÷2)2+40×100
=3.14×400+4000
=1256+4000
=5256(平方米)
答:运动场的周长是325.6米,运动场的面积是5256平方米。
【点睛】解答本题的关键是熟记圆的周长公式和面积公式以及长方形面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(备战期末)专题04:圆-2023-2024学年数学五年级下册苏教版
一、选择题
1.小明在游乐场骑玩具车,在平直的轨道上,车有规律的上下起伏。下面说法,错误的是( )。
A.车轮不是圆形的 B.车轴没有装在圆形车轮的圆心处
C.A、B都有可能 D.车把松动了
2.美术老师用彩色卡纸制作了一个2022年冬奥会吉祥物“冰墩墩”,制作时需要把一个直径4厘米的圆形纸片剪成两个半圆,这两个半圆的周长和是( )厘米。
A.10.28 B.12.56 C.16.56 D.20.56
3.如图,大圆01的半径是5厘米,小圆02的半径是2厘米。如小圆02围绕大圆01的圆周滚动一周,小圆O2的圆心移动了( )厘米。
A.14π B.21π C.24π D.49π
4.从3块边长都是12厘米的正方形铁皮中,分别剪去如下图所示的黑色部分,剩下的铁皮面积( )。
A.①大 B.②大 C.③大 D.一样大
5.下面关于圆周率的说法,错误的是( )。
A.是圆的周长与它的直径的比值
B.大圆和小圆相比,大圆的的值要大一些
C.3.14是的一个近似值
D.是一个无限不循环小数
6.李明去披萨店点了一个12寸的披萨,过了一会服务员过来说:“不好意思,现在做不了12寸的,您看换成2个6寸的可以吗?反正一样大!”你认为呢?(说明:12寸、6寸,是指披萨的直径)( )。
A.12寸的大 B.2个6寸的大 C.一样大 D.无法确定
二、填空题
7.在钟面上画一画,涂一涂,分针从12起,走10分钟、15分钟和45分钟所经过的部分都可看作是( ),圆心角分别是( )、( )、( )。
8.从一个圆中剪去一个圆心角为60°的扇形,剪去的部分占圆的( )。(填分数)
9.一个钟面上,时针长6厘米,分针长10厘米。从3:15到3:40,分针扫过的区域可以看作扇形,这个扇形的圆心角是( )°,半径是( )厘米。
10.图中有( )个扇形,每个扇形的圆心角的度数分别是( ),半径分别是( )。
11.如图,平行四边形的面积比长方形的面积大6cm2,圆的面积是( )cm2。
12.小刘在边长6厘米的大正方形中,画出最大圆的面积是( )平方厘米,他在圆内又剪一个最大的正方形,那么阴影部分面积是( )平方厘米。
三、判断题
13.车轮的轴安装在圆心处,是因为这点到车轮上的距离处处相等。( )
14.把一个圆平均分成16份,拼成一个近似的长方形,转化后周长不变。( )
15.在长6厘米、宽4厘米的长方形里画一个最大的半圆,半圆的半径是3厘米。( )
16.圆心角是60度的扇形的面积是它所在圆的面积的。( )
17.直径是6分米的圆比半径是4分米的圆要大一些。( )
四、计算题
18.计算下图中阴影部分的面积。
19.求涂色部分的面积。
五、解答题
20.幸福小区有一个圆形花坛,量得花坛一周的篱笆长是25.12米。这个花坛的占地面积是多少平方米?
21.用一条15米长的绳子围绕一棵树干绕了8圈,还余下2.44米,这棵树干的横截面直径大约是多少米?
22.李大爷用9.42米长的篱笆靠墙角围了一个最大的养鸡场(如图所示),这个养鸡场的面积是多少平方米?
23.下图中每个正方形的边长为1厘米。
(1)以点O(4,3)为圆心,画一个直径为4厘米的圆,并在图上标出圆O的位置。
(2)把圆O向右平移( )格,使圆O成为正方形内最大的圆。
(3)画出平移后圆与正方形组合图形的所有对称轴。
24.下图是一个运动场,两端是半圆形,中间是长方形。这个运动场的周长和面积各是多少?
参考答案:
1.D
【分析】根据圆的特征,逐项分析,进行解答即可。
【详解】根据在平直的轨道上,车有规律的上下起伏分析如下:
A.车轮不是圆形的,有可能造成有规律的上下起伏,原题干说法正确;
B.车轴没有装在圆形车轮的圆心处,有可能造成车有规律的上下起伏,原题干说法正确;
C.车轮不是圆形的,车轴没有装在圆形车轮的圆心处,都有可能造成车有规律的上下起伏,原题干说法正确;
D.车把松动一般不会造成车有规律的上下起伏,原题干说法错误。
小明在游乐场骑玩具车,在平直的轨道上,车有规律的上下起伏。下面说法,错误的车把松动了。
故答案为:D
【点睛】本题考查圆的特征的知识,结合题意分析解答即可。
2.D
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径,所以这两个半圆的周长和比圆的周长增加两条直径的长度,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
故答案为:D
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的公式及应用。
3.A
【分析】通过观察图形可知,小圆O2围绕大圆O1的圆周滚动一周,小圆O2的圆心移动的距离等于半径为(5+2)厘米的圆的周长,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】π×(5+2)×2
=π×7×2
=14π(厘米)
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
4.D
【分析】由题意可知:
图①:剩下的铁皮面积=正方形的面积-一个大圆的面积;
图②:剩下的铁皮面积=正方形的面积-9个小圆的面积;
图③:剩下的铁皮面积=正方形的面积-4个小扇形的面积(每个小扇形相当于圆的面积,4个小扇形就相当于一个圆的面积);
【详解】正方形的面积:12×12=144(平方厘米)
图①:圆的半径12÷2=6(厘米)
剩下的铁皮面积:
144-3.14×
=144-113.04
=30.96(平方厘米)
图②:圆的半径
12÷3÷2
=4÷2
=2(厘米)
剩下的铁皮面积:
144-3.14××9
=144-12.56×9
=144-113.04
=30.96(平方厘米)
图③:圆的半径12÷2=6(厘米)
剩下的铁皮面积:
144-3.14×
=144-113.04
=30.96(平方厘米)
图①剩余面积=图②剩余面积=图③剩余面积
故答案为:D
【点睛】解答此题的关键是明白:剩下的铁皮的面积=正方形的面积-圆的面积,只要补充上直径的长度,即可求解。
5.B
【分析】根据圆周率的意义:圆的周长和它的直径的比值,叫做圆周率;用字母π表示;π是一个无限不循环的小数,据此解答。
【详解】A.根据圆周率的意义可知,π是圆的周长与它的直径的比值;原题干说法正确;
B.圆的大小与圆周率无关,圆周率不会随着圆的大小的改变而改变;原题干说法错误;
C.3.14是π的一个近似值,原题干说法正确;
D.π是一个无限不循环小数,原题干说法正确。
故答案为:B
【点睛】根据圆周率的意义进行解答。
6.A
【分析】因为披萨厚度一样,所以只要比较12寸的和两个6寸的底面积的大小即可,根据圆的公式S=πr2,把具体数据代入计算即可。
【详解】12寸披萨的面积:
3.14×(12÷2)2
=3.14×36
=113.04(平方英寸)
2个6寸披萨的面积:
3.14×(6÷2)2×2
=3.14×9×2
=56.52(平方英寸)
因为113.04平方英寸>56.52平方英寸,所以12寸披萨的面积大。
故答案为:A
【点睛】此题主要考查圆面积公式的灵活运用及小数大小的比较。
7.扇形;60°、90°、270°
【分析】根据扇形的定义是一条弧和经过这条弧两端的两条半径所围成的图形,由此结合题意即可得出答案;钟面分成12个大格,分针每过一个大格是5分钟;分针指向3,走10分钟、15分钟和45分钟分别走了10÷5=2个大格,15÷5=3个大格,45÷5=9个大格;根据钟表的认识,角的分类,钟面上的分针从12起走一圈走了60分钟;走过的角是周角;是360度;钟面上12个数字把钟面平均分成12份,每份所对应的圆周角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,依此解答。
【详解】根据扇形的定义,可得分针从12起,走10分钟、15分钟和45分钟所经过的部分都可看作是扇形。
如图:
10÷5=2
15÷5=3
45÷5=9
2×30°=60°
3×30°=90°
9×30°=270°
圆心角分别是60°、90°、270°。
【点睛】本题考查了认识平面图形的知识,属于基础题,解题关键是要求指向旋转了多少度,关键是看走了几个数字。
8.
【分析】周角是360°,用60°除以360°即可表示剪去部分占圆的几分之几。
【详解】60÷360=
即剪去的部分占圆的。
【点睛】此题解答关键是明确:周角是360°,根据求一个数是另一个数的几分之几,用除法解答。
9. 150 10
【分析】钟面上一个大格是5分钟,是30°,从3:15到3:40,是25分钟,25÷5=5,走过来5个大格,再用一个大格的度数×5,即可求出这个扇形的圆心角的度数,因为是分针扫过的区域,所以扇形的半径等于分针的长度,据此解答。
【详解】3:15到3:40,是25分钟。
30°×(25÷5)
=30°×5
=150°
一个钟面上,时针长6厘米,分针长10厘米。从3:15到3:40,分针扫过的区域可以看作扇形,这个扇形的圆心角是150°,半径是10厘米。
【点睛】本题主要考查钟表时间与扇形圆心角的关系,关键是求出分针从3:15到3:40,走过的时间。
10. 3 180°、180°、90° 2厘米、2厘米、4厘米
【分析】根据扇形的意义:一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形(半圆和直径的组合也是扇形),它是由圆周的一部分与它所对应的圆心角围成,据此解答。
【详解】4÷2=2(厘米)
图中有3个扇形,左边图有2个扇形,右边图有1个扇形;左边2个扇形的圆心角是180度,右边扇形的圆心角是90°;左边扇形半径是2厘米,右边扇形半径是4厘米。
【点睛】熟练掌握扇形的特征是解答本题的关键。
11.28.26
【分析】长方形的长、平行四边形的高、圆的直径相等。由平行四边形的面积比长方形的面积大6 cm2,可知平行四边形的高是6÷(5-4)=6(cm),所以圆的半径是:6÷2=3(cm);再根据圆的面积公式:,即可求出圆的面积。
【详解】6÷(5-4)
=6÷1
=6(cm)
6÷2=3(cm)
3.14×32
=3.14×9
=28.26(cm2)
所以,圆的面积是28.26cm2。
【点睛】正确理解图意,熟记长方形、平行四边形、圆的面积计算公式,是解答此题的关键。
12. 28.26 10.26
【分析】观察图形可知,大正方形中最大圆的直径等于正方形的边长,是6厘米,则半径是6÷2=3(厘米),根据圆的面积=πr2即可求出这个圆的面积。
如下图所示,把圆中最大的正方形平均分成2个完全相同的三角形,三角形的一条底等于圆的直径,对应的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2求出圆内最大正方形的面积。最后用圆的面积减去这个正方形的面积即可求出阴影部分的面积。
【详解】6÷2=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
28.26-6×3÷2×2
=28.26-18
=10.26(平方厘米)
则画出最大圆的面积是28.26平方厘米,阴影部分面积是10.26平方厘米。
【点睛】本题考查了圆和三角形面积的运算。把圆内最大正方形的面积转化为两个三角形的面积进行计算是解题的关键。
13.√
【分析】根据半径的定义:连接圆心和圆上任意一点的线段,叫做半径;同一个圆里,有无数条半径,所有半径长度都相等。以此判断。
【详解】车轮的轴安装在圆心处,从圆心到车轮上的距离就是圆的半径,因为所有的半径长度都相等,所以这点到车轮上的距离处处相等。
故答案为:√
【点睛】此题主要考查了圆的特征,同一个圆内,所有的半径都相等。
14.×
【分析】根据圆拼成的长方形的过程可知,近似长方形的长等于圆周长()的一半,宽等于圆的半径,然后根据长方形的周长计算列式与圆的周长公式进行比对,据此解答。
【详解】长:πr,宽:r;
长方形周长=(长+宽)×2=(πr+r)×2=2πr+2r
因为圆的周长=2πr,所以周长发生了改变。
所以原题说法错误。
【点睛】此题主要考查了学生对圆进行切割拼组后的长方形的周长变化规律的了解与实际推算。
15.√
【分析】根据题意可知,在一个长方形里画一个最大的半圆,半圆的直径等于长方形的长,以此解答。
【详解】由于在一个长方形里画一个最大的半圆,半圆的直径等于长方形的长,那么半圆的半径就等于6÷2=3(厘米)
所以原题说法正确。
【点睛】此题关键在于理解长方形内最大的半圆的直径等于长方形的长。
16.√
【分析】扇形的面积=扇形所在圆的面积× 据此判断即可。
【详解】60÷360=,所以圆心角是60度的扇形的面积是它所在圆的面积的。原题说法正确。
【点睛】此题考查有关扇形的面积计算,掌握扇形面积计算公式是解题关键。
17.×
【分析】分别计算直径是6分米的圆和半径是4分米的圆的面积,比较大小。
【详解】直径是6分米的圆:3.14×(6÷2)2=28.26(平方分米)
半径是4分米的圆:3.14×42=50.24(平方分米);50.24>28.26
直径是6分米的圆比半径是4分米的圆要小一些。原题说法错误。
【点睛】两个圆,直径(半径)较大的圆,面积和周长都较大。
18.3.44
【分析】根据对图形的分析,阴影部分面积为正方形面积减去圆的面积,该正方体边长为4,该圆的直径为4。再根据正方形面积公式:正方形面积=边长×边长,圆的半径=直径÷2,圆的面积公式为:S=r2,将数据代入求解即可。
【详解】由分析可得:
圆半径为:4÷2=2
阴影部分面积为:
4×4-3.14×22
=16-3.14×4
=16-12.56
=3.44
19.113.04cm2
【分析】根据题意,涂色部分的面积,即为环形面积,根据环形面积公式:S=π(R2-r2),代入数据求值即可。
【详解】由分析可得:
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(cm2)
20.50.24平方米
【分析】由题意可知:圆形花坛的周长为25.12米,代入圆的周长公式:C=2πr求出半径,再代入圆的面积公式:S=πr2计算即可。
【详解】25.12÷3.14÷2
=8÷2
=4(米)
3.14×42
=3.14×16
=50.24(平方米)
答:这个花坛的占地面积是50.24平方米。
【点睛】本题考查圆的周长、面积公式的灵活运用,牢记公式是解题的关键。
21.0.5米
【分析】用这根绳子的总长度-余下的长度,即15-2.44,求出绕树干绕8圈的长度,再除以8,求出绕树干绕一圈的长度,也就是这个树的周长,再根据圆的周长公式:周长=π×直径,直径=周长÷π,代入数据,即可解答。
【详解】(15-2.44)÷8÷3.14
=12.56÷8÷3.14
=1.57÷3.14
=0.5(米)
答:这棵树干的横截面直径大约是0.5米。
【点睛】解答本题的关键是求出绳子绕树干绕一圈的长度。
22.28.26平方米
【分析】观察图形可知,这个圆平均分成了4份,其中一份的圆的弧长是9.42米,由此可知,用9.42×4,求出这个圆的周长;根据周长公式:周长=π×半径×2;半径=周长÷π÷2,代入数据,求出圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出这个圆的面积,再除以4,即可求出这个养鸡场的面积,据此解答。
【详解】9.42×4÷3.14÷2
=37.68÷3.14÷2
=12÷2
=6(米)
3.14×62÷4
=113.04÷4
=28.26(平方米)
答:这个养鸡场的面积是28.26平方米。
【点睛】解答本题的关键明确这个圆被平均分成了4份,进而利用圆的周长公式和面积公式进行解答。
23.见详解
【分析】(1)要画直径为4厘米的圆,则半径为(4÷2=2)厘米。结合数对知识,第一个数表示列,第二个数表示行,把圆规的两脚分开,定好两脚间距离是2厘米,把有针尖的一只脚固定在一(4,3)上;带有铅笔的那只脚绕点旋转一周即可完成画圆。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。根据平移的特征,把圆O向右平移,使圆O成为正方形内最大的圆。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左边图形的关键对称点,依次连接即可;据此画出平移后圆与正方形组合图形的所有对称轴。
【详解】(1)(3)如下图:
(2)把圆O向右平移8格,使圆O成为正方形内最大的圆。
【点睛】此题考查的知识点:数对与位置、平移的特征、对称轴的知识。
24.周长:325.6米;面积:5256平方米
【分析】根据题意可知,长方形的宽等于圆的直径,运动场的周长=圆的周长+(长方形的长×2);根据圆的周长公式:周长=π×直径;代入数据,求出运动场的周长;运动场的面积=圆的面积+长方形的面积,根据圆的面积公式:面积=π×半径2,长方形面积公式:面积=长×宽,代入数据,即可求出运动场面积。
【详解】周长:3.14×40+2×100
=125.6+200
=325.6(米)
面积:3.14×(40÷2)2+40×100
=3.14×400+4000
=1256+4000
=5256(平方米)
答:运动场的周长是325.6米,运动场的面积是5256平方米。
【点睛】解答本题的关键是熟记圆的周长公式和面积公式以及长方形面积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
