2024年四川省南充市中考数学试题(含答案)
文档属性
| 名称 | 2024年四川省南充市中考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 20:53:16 | ||
图片预览




文档简介
南充市二○二四年初中学业水平考试
数学试题
(满分150分,时间120分钟)
注意事项:
1.答题前将姓名、座位号、身份证号、准考证号填在答题卡指定位置;
2.所有解答内容均须涂、写在答题卡上;
3.选择题须用2B铅笔将答题卡相应题号对应选项涂黑,若需改动,须擦净另涂;
4.填空题、解答题在答题卡对应题号位置用0.5毫米黑色字迹笔书写.
一、选择题(本大题共10个小题,每小题4分,共40分)每小题都有代号为A,B,C,D四个答案选项,其中只有一个是正确的。请根据正确选项的代号填涂答题卡对应位置,填涂正确记4分,不涂、错涂或多涂记0分。
1.如图,数轴上表示的点是( )
A.点A B.点B C.点C D.点D
2.学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩(百分制人选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
3.如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.如图,在中,,AD平分交BC于点D,点E为边AB上一点,则线段DE长度的最小值为( )
A. B. C.2 D.3
6.我国古代《算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中.一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房、设有客房x间,客人y人,则可列方程组为( )
A. B. C. D.
7.若关于x的不等式组的解集为,则m的取值范围是( )
A. B. C. D.
8.如图,己知线段AB,按以下步骤作图:①过点B作,使,连接AC;②以点C为圆心,以BC长为半径画弧,交AC于点D;③以点A为圆心,以AD长为半径画弧,交AB于点E.若,则m的值为( )
A. B. C. D.
9.当时,一次函数有最大值6,则实数m的值为( )
A.或0 B.0或1 C.或 D.或1
10.如图是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成.在正方形ABCD中,.下列三个结论:①若,则;②若的面积是正方形EFGH面积的3倍,则点F是AG的三等分点;③将绕点A逆时针旋转得到,则的最大值为.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共6个小题,每小题4分,共24分)请将答案填在答题卡对应的横线上。
11.计算的结果为___________.
12.若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为___________.
13.如图,AB是的直径,位于AB两侧的点C,D均在上,,则______度.
14.已知m是方程的一个根,则的值为___________.
15.如图,在矩形ABCD中,E为AD边上一点,,将沿BE折叠得,连接CF,DF,若CF平分,,则DF的长为___________.
16.己知抛物线与x轴交于两点A,B(A在B的左侧),抛物线与x轴交于两点C,D(C在D的左侧),且.下列四个结论:①与交点为;②;③;④A,D两点关于对称.其中正确的结论是___________(填写序号)
三、解答题(本大题共9个小题,共86分)解答应写出必要的文字说明、证明过程或演算步骤。
17.(8分)先化简,再求值:,其中.
18.(8分)如图,在中,点D为BC边的中点,过点B作交AD的延长线于点E.
(1)求证:.
(2)若,求证:,
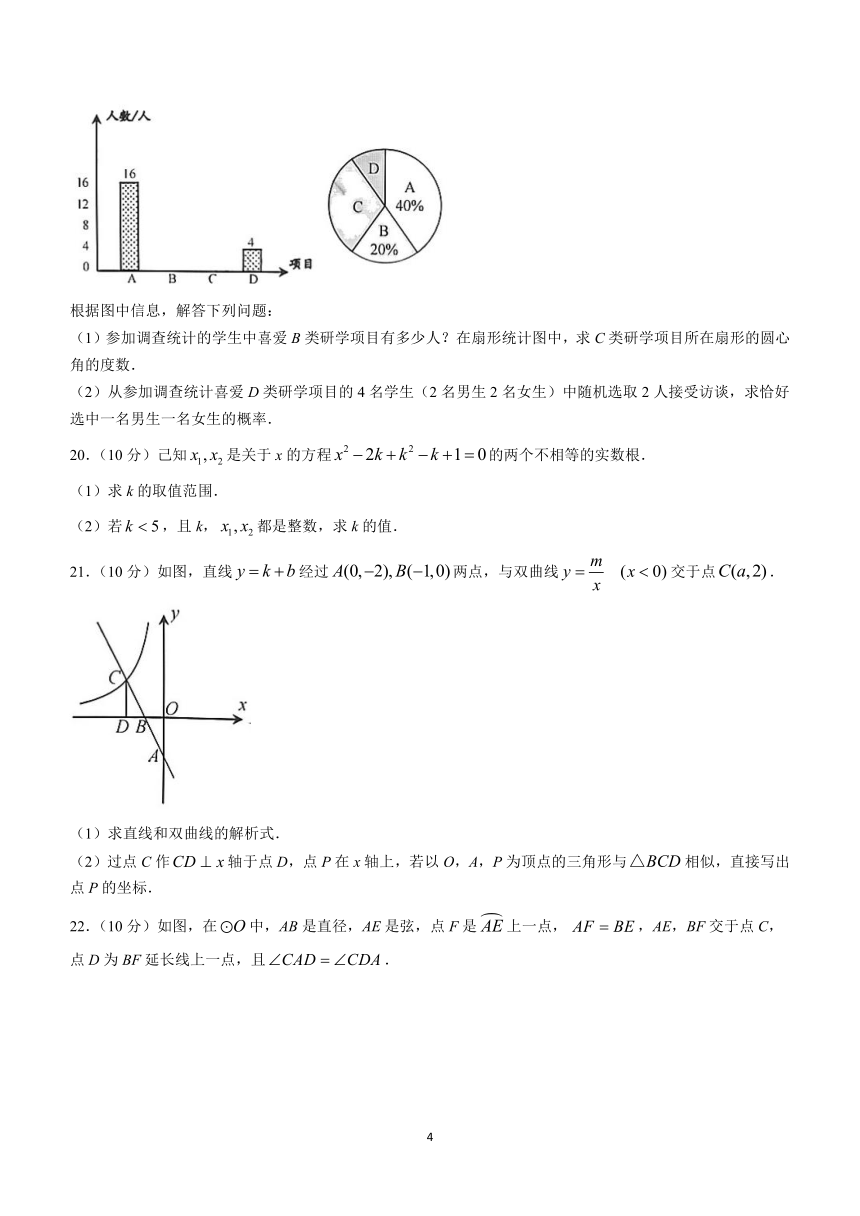
19.(8分)某研学基地开设有A,B,C,D四类研学项目.为了解学生对四类研学项目的喜爱情况,随机抽取部分参加完研学项目的学生进行调查统计(每名学生必须选择一项,并且只能选择一项),并将调查结果绘制成两幅不完整的统计图,(如图).
根据图中信息,解答下列问题:
(1)参加调查统计的学生中喜爱B类研学项目有多少人?在扇形统计图中,求C类研学项目所在扇形的圆心角的度数.
(2)从参加调查统计喜爱D类研学项目的4名学生(2名男生2名女生)中随机选取2人接受访谈,求恰好选中一名男生一名女生的概率.
20.(10分)己知是关于x的方程的两个不相等的实数根.
(1)求k的取值范围.
(2)若,且k,都是整数,求k的值.
21.(10分)如图,直线经过两点,与双曲线交于点.
(1)求直线和双曲线的解析式.
(2)过点C作轴于点D,点P在x轴上,若以O,A,P为顶点的三角形与相似,直接写出点P的坐标.
22.(10分)如图,在中,AB是直径,AE是弦,点F是上一点,,AE,BF交于点C,点D为BF延长线上一点,且.
(1)求证:AD是的切线.
(2)若,求的半径长.
23.(10分)2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价50元/件,B类特产进价60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.
(1)求A类特产和B类特产每件的售价各是多少元?
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元?(利润=售价-进价)
24.(10分)如图,正方形ABCD边长为,点E为对角线AC上一点,,点P在AB边上以的速度由点A向点B运动,同时点Q在BC边上以的速度由点C向点B运动,设运动时间为t秒().
(1)求证:.
(2)当是直角三角形时,求t的值.
(3)连接AQ,当时,求的面积.
25.(12分)
已知抛物线与x轴交于点.
图1 图2
(1)求抛物线的解析式.
(2)如图1,抛物线与y轴交于点C,点P为线段OC上一点(不与端点重合),直线PA,PB分别交抛物线于点E,D,设面积为,面积为,求的值.
(3)如图2,点K是抛物线对称轴与x轴的交点,过点K的直线(不与对称轴重合)与抛物线交于点M,N,过抛物线顶点G作直线轴,点Q是直线l上一动点.求的最小值.
南充市二○二四年初中学业水平考试
数学参考答案及评分意见
说明:
1.阅卷前认真阅读参考答案和评分意见,明确评分标准,不得随意拔高或降低标准。
2.全卷满分150分,参考答案和评分意见所给分数表示考生正确完成当前步骤时应得的累加分数。
3.参考答案和评分意见仅是解答的一种,如果考生的解答与参考答案不同,只要正确就应该参照评分意见给分。合理精简解答步骤,其简化部分不影响评分。
4.要坚持每题评阅到底.如果考生解答过程发生错误,只要不降低后继部分的难度且后继部分再无新的错误,可得不超过后继部分应得分数的一半;如果发生第二次错误,后面部分不予得分;若是相对独立的得分点,其中一处错误不影响其它得分点的评分。
一、选择题(本大题共10个小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D C D B A A D
二、填空题(本大题共6个小题,每小题4分,共24分)
11.1 12.7 13.75 14. 15. 16.①②④
三、解答题(本大题共9个小题,共86分)
17.解:原式 (4分)
(5分)
. (6分)
当时,原式. (8分)
18.(1)证明:为BC的中点,. (1分)
. (3分)
在和中,. (6分)
(2)证明:. (7分)
垂直平分AE,. (8分)
19.解:(1)(人). (2分)
(度). (4分)
答:喜爱B类研学项目有8人,C类研学项目所在扇形的圆心角的度数为108°.
(2)喜爱D类研学项目的4名学生分别记为男1,男2,女1,女2,列表如下:
第2位第1位 男1 男2 女1 女2
男1 男1男2 男1女1 男1女2
男2 男2男1 男2女1 男2女2
女1 女1男1 女1男2 女1女2
女2 女2男1 女2男2 女2女1
由表可知,抽选2名学生共有12种等可能结果,抽中一名男生和一名女生(记作事件M)共8种可能.
.(8分)
答:抽中一名男生和一名女生的概率为.
20.解:(1)原方程有两个不相等的实数根,. (2分)
(4分)
. (5分)
解得. (6分)
(2)整数k的值为2,3,4. (7分)
当时,方程为,解得. (9分)
当或4时,此时方程解不为整数. (10分)
综上所述,k的值为2.
21.解:(1)点在直线上,
(2分)
解得直线解析式为. (4分)
点在直线上,
,即点C为. (5分)
双曲线过点. (7分)
双曲线解析式为.
(2)点P坐标为或或或. (10分)
22.(1)证明:. (1分)
,
. (3分)
即. (4分)
是的切线. (5分)
(2)解:连接AF.. (6分)
是直径,. (7分)
在中,. (8分)
. (9分)
又AB是直径的半径长为. (10分)
23.解:(1)设每件A类特产的售价为x元,则每件B类特产的售价为元.
根据题意得. (1分)
解得. (2分)
每件B类特产的售价(元). (3分)
答:A类特产的售价为60元/件,B类特产的售价为72元/件.
(2)由题意得(). (5分)
(3) (7分)
. (8分)
当时,w有最大值1840. (9分)
即A类特产每件售价降价2元时,每天销售利润最犬,最大利润为1840元. (10分)
24.(1)证明:四边形ABCD是正方形,. (1分)
, (2分)
. (3分)
(2)解:过点E作于点M,过点E作于点N.
由题意知.
.
,即,
,即,
,即. (4分)
①当时,有.
即,整理得.
解得(不合题意,舍去). (5分)
②当时,有.
即,整理得,解得.
③当时,有.
即,整理得,该方程无实数解.
综上所述,当是直角三角形时,t的值为秒或2秒.(6分)
(3)解:过点A作,交CB的延长线于点F,连接FE交AQ于点G.
,
. (7分)
又.
.
.
. (8分)
.
,即,
是等腰直角三角形. (9分)
. (10分)
25.解:(1)由题意得 (2分)
解得抛物线的解析式为. (3分)
(2)设,直线AP为,据题意得
解得
,联立得
解得或 (4分)
同理可得. (5分)
. (6分)
.
. (7分)
(3)设直线MN为.由得
. (8分)
设.
联立直线MN与抛物线
得.
根据根与系数的关系可得:.(9分)
作点N关于直线l的对称点,连接.
由题意得直线,则.
.
过M点作于F,则.
则. (10分)
在中,
. (11分)
即当时,,此时.
故的最小值为.(12分)
数学试题
(满分150分,时间120分钟)
注意事项:
1.答题前将姓名、座位号、身份证号、准考证号填在答题卡指定位置;
2.所有解答内容均须涂、写在答题卡上;
3.选择题须用2B铅笔将答题卡相应题号对应选项涂黑,若需改动,须擦净另涂;
4.填空题、解答题在答题卡对应题号位置用0.5毫米黑色字迹笔书写.
一、选择题(本大题共10个小题,每小题4分,共40分)每小题都有代号为A,B,C,D四个答案选项,其中只有一个是正确的。请根据正确选项的代号填涂答题卡对应位置,填涂正确记4分,不涂、错涂或多涂记0分。
1.如图,数轴上表示的点是( )
A.点A B.点B C.点C D.点D
2.学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩(百分制人选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
3.如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.如图,在中,,AD平分交BC于点D,点E为边AB上一点,则线段DE长度的最小值为( )
A. B. C.2 D.3
6.我国古代《算法统宗》里有这样一首诗“我问开店李三公,众客都来到店中.一房七客多七客,一房九客一房空.”诗中后面两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房、设有客房x间,客人y人,则可列方程组为( )
A. B. C. D.
7.若关于x的不等式组的解集为,则m的取值范围是( )
A. B. C. D.
8.如图,己知线段AB,按以下步骤作图:①过点B作,使,连接AC;②以点C为圆心,以BC长为半径画弧,交AC于点D;③以点A为圆心,以AD长为半径画弧,交AB于点E.若,则m的值为( )
A. B. C. D.
9.当时,一次函数有最大值6,则实数m的值为( )
A.或0 B.0或1 C.或 D.或1
10.如图是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成.在正方形ABCD中,.下列三个结论:①若,则;②若的面积是正方形EFGH面积的3倍,则点F是AG的三等分点;③将绕点A逆时针旋转得到,则的最大值为.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(本大题共6个小题,每小题4分,共24分)请将答案填在答题卡对应的横线上。
11.计算的结果为___________.
12.若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为___________.
13.如图,AB是的直径,位于AB两侧的点C,D均在上,,则______度.
14.已知m是方程的一个根,则的值为___________.
15.如图,在矩形ABCD中,E为AD边上一点,,将沿BE折叠得,连接CF,DF,若CF平分,,则DF的长为___________.
16.己知抛物线与x轴交于两点A,B(A在B的左侧),抛物线与x轴交于两点C,D(C在D的左侧),且.下列四个结论:①与交点为;②;③;④A,D两点关于对称.其中正确的结论是___________(填写序号)
三、解答题(本大题共9个小题,共86分)解答应写出必要的文字说明、证明过程或演算步骤。
17.(8分)先化简,再求值:,其中.
18.(8分)如图,在中,点D为BC边的中点,过点B作交AD的延长线于点E.
(1)求证:.
(2)若,求证:,
19.(8分)某研学基地开设有A,B,C,D四类研学项目.为了解学生对四类研学项目的喜爱情况,随机抽取部分参加完研学项目的学生进行调查统计(每名学生必须选择一项,并且只能选择一项),并将调查结果绘制成两幅不完整的统计图,(如图).
根据图中信息,解答下列问题:
(1)参加调查统计的学生中喜爱B类研学项目有多少人?在扇形统计图中,求C类研学项目所在扇形的圆心角的度数.
(2)从参加调查统计喜爱D类研学项目的4名学生(2名男生2名女生)中随机选取2人接受访谈,求恰好选中一名男生一名女生的概率.
20.(10分)己知是关于x的方程的两个不相等的实数根.
(1)求k的取值范围.
(2)若,且k,都是整数,求k的值.
21.(10分)如图,直线经过两点,与双曲线交于点.
(1)求直线和双曲线的解析式.
(2)过点C作轴于点D,点P在x轴上,若以O,A,P为顶点的三角形与相似,直接写出点P的坐标.
22.(10分)如图,在中,AB是直径,AE是弦,点F是上一点,,AE,BF交于点C,点D为BF延长线上一点,且.
(1)求证:AD是的切线.
(2)若,求的半径长.
23.(10分)2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价50元/件,B类特产进价60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.
(1)求A类特产和B类特产每件的售价各是多少元?
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元?(利润=售价-进价)
24.(10分)如图,正方形ABCD边长为,点E为对角线AC上一点,,点P在AB边上以的速度由点A向点B运动,同时点Q在BC边上以的速度由点C向点B运动,设运动时间为t秒().
(1)求证:.
(2)当是直角三角形时,求t的值.
(3)连接AQ,当时,求的面积.
25.(12分)
已知抛物线与x轴交于点.
图1 图2
(1)求抛物线的解析式.
(2)如图1,抛物线与y轴交于点C,点P为线段OC上一点(不与端点重合),直线PA,PB分别交抛物线于点E,D,设面积为,面积为,求的值.
(3)如图2,点K是抛物线对称轴与x轴的交点,过点K的直线(不与对称轴重合)与抛物线交于点M,N,过抛物线顶点G作直线轴,点Q是直线l上一动点.求的最小值.
南充市二○二四年初中学业水平考试
数学参考答案及评分意见
说明:
1.阅卷前认真阅读参考答案和评分意见,明确评分标准,不得随意拔高或降低标准。
2.全卷满分150分,参考答案和评分意见所给分数表示考生正确完成当前步骤时应得的累加分数。
3.参考答案和评分意见仅是解答的一种,如果考生的解答与参考答案不同,只要正确就应该参照评分意见给分。合理精简解答步骤,其简化部分不影响评分。
4.要坚持每题评阅到底.如果考生解答过程发生错误,只要不降低后继部分的难度且后继部分再无新的错误,可得不超过后继部分应得分数的一半;如果发生第二次错误,后面部分不予得分;若是相对独立的得分点,其中一处错误不影响其它得分点的评分。
一、选择题(本大题共10个小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D C D B A A D
二、填空题(本大题共6个小题,每小题4分,共24分)
11.1 12.7 13.75 14. 15. 16.①②④
三、解答题(本大题共9个小题,共86分)
17.解:原式 (4分)
(5分)
. (6分)
当时,原式. (8分)
18.(1)证明:为BC的中点,. (1分)
. (3分)
在和中,. (6分)
(2)证明:. (7分)
垂直平分AE,. (8分)
19.解:(1)(人). (2分)
(度). (4分)
答:喜爱B类研学项目有8人,C类研学项目所在扇形的圆心角的度数为108°.
(2)喜爱D类研学项目的4名学生分别记为男1,男2,女1,女2,列表如下:
第2位第1位 男1 男2 女1 女2
男1 男1男2 男1女1 男1女2
男2 男2男1 男2女1 男2女2
女1 女1男1 女1男2 女1女2
女2 女2男1 女2男2 女2女1
由表可知,抽选2名学生共有12种等可能结果,抽中一名男生和一名女生(记作事件M)共8种可能.
.(8分)
答:抽中一名男生和一名女生的概率为.
20.解:(1)原方程有两个不相等的实数根,. (2分)
(4分)
. (5分)
解得. (6分)
(2)整数k的值为2,3,4. (7分)
当时,方程为,解得. (9分)
当或4时,此时方程解不为整数. (10分)
综上所述,k的值为2.
21.解:(1)点在直线上,
(2分)
解得直线解析式为. (4分)
点在直线上,
,即点C为. (5分)
双曲线过点. (7分)
双曲线解析式为.
(2)点P坐标为或或或. (10分)
22.(1)证明:. (1分)
,
. (3分)
即. (4分)
是的切线. (5分)
(2)解:连接AF.. (6分)
是直径,. (7分)
在中,. (8分)
. (9分)
又AB是直径的半径长为. (10分)
23.解:(1)设每件A类特产的售价为x元,则每件B类特产的售价为元.
根据题意得. (1分)
解得. (2分)
每件B类特产的售价(元). (3分)
答:A类特产的售价为60元/件,B类特产的售价为72元/件.
(2)由题意得(). (5分)
(3) (7分)
. (8分)
当时,w有最大值1840. (9分)
即A类特产每件售价降价2元时,每天销售利润最犬,最大利润为1840元. (10分)
24.(1)证明:四边形ABCD是正方形,. (1分)
, (2分)
. (3分)
(2)解:过点E作于点M,过点E作于点N.
由题意知.
.
,即,
,即,
,即. (4分)
①当时,有.
即,整理得.
解得(不合题意,舍去). (5分)
②当时,有.
即,整理得,解得.
③当时,有.
即,整理得,该方程无实数解.
综上所述,当是直角三角形时,t的值为秒或2秒.(6分)
(3)解:过点A作,交CB的延长线于点F,连接FE交AQ于点G.
,
. (7分)
又.
.
.
. (8分)
.
,即,
是等腰直角三角形. (9分)
. (10分)
25.解:(1)由题意得 (2分)
解得抛物线的解析式为. (3分)
(2)设,直线AP为,据题意得
解得
,联立得
解得或 (4分)
同理可得. (5分)
. (6分)
.
. (7分)
(3)设直线MN为.由得
. (8分)
设.
联立直线MN与抛物线
得.
根据根与系数的关系可得:.(9分)
作点N关于直线l的对称点,连接.
由题意得直线,则.
.
过M点作于F,则.
则. (10分)
在中,
. (11分)
即当时,,此时.
故的最小值为.(12分)
同课章节目录
