2024年黑龙江省佳木斯市中考模拟数学试题(含答案)
文档属性
| 名称 | 2024年黑龙江省佳木斯市中考模拟数学试题(含答案) | 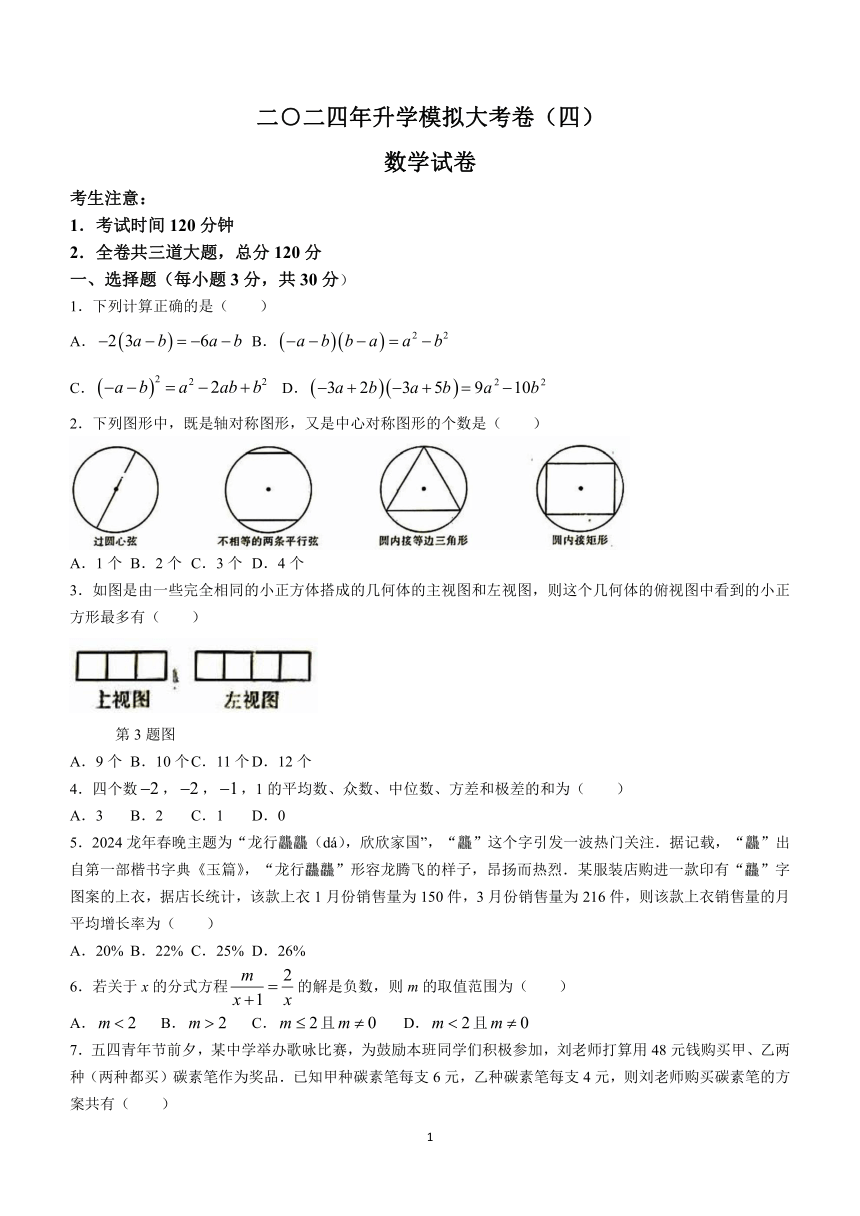 | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 11:25:38 | ||
图片预览





文档简介
二○二四年升学模拟大考卷(四)
数学试卷
考生注意:
1.考试时间120分钟
2.全卷共三道大题,总分120分
一、选择题(每小题3分,共30分)
1.下列计算正确的是( )
A. B.
C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,则这个几何体的俯视图中看到的小正方形最多有( )
第3题图
A.9个 B.10个 C.11个 D.12个
4.四个数,,,1的平均数、众数、中位数、方差和极差的和为( )
A.3 B.2 C.1 D.0
5.2024龙年春晚主题为“龙行龘龘(dá),欣欣家国”,“龘”这个字引发一波热门关注.据记载,“龘”出自第一部楷书字典《玉篇》,“龙行龘龘”形容龙腾飞的样子,昂扬而热烈.某服装店购进一款印有“龘”字图案的上衣,据店长统计,该款上衣1月份销售量为150件,3月份销售量为216件,则该款上衣销售量的月平均增长率为( )
A.20% B.22% C.25% D.26%
6.若关于x的分式方程的解是负数,则m的取值范围为( )
A. B. C.且 D.且
7.五四青年节前夕,某中学举办歌咏比赛,为鼓励本班同学们积极参加,刘老师打算用48元钱购买甲、乙两种(两种都买)碳素笔作为奖品.已知甲种碳素笔每支6元,乙种碳素笔每支4元,则刘老师购买碳素笔的方案共有( )
A.4种 B.3种 C.2种 D.1种
8.如图,点A在反比例函数的图象上,点B在反比例函数的图象上,轴,交x轴于点C,连接,取的中点D,连接,则(阴影部分)的面积为( )
第8题图
A.3 B.8 C.4 D.2
9.如图,点D在的边上,,,,若,则的长为( )
第9题图
A.2.5 B. C.2 D.3
10.如图,E是矩形的边的中点,于点F,的延长线交于点G,连接,则下列结论:①;②;③若,,则;④;⑤图中相似三角形只有6对.其中正确结论的序号是( )
第10题图
A.①②③ B.②③④ C. ( mailto:A.023%09B.@3%09C.@5 )①④⑤ D.①②③④⑤
二、填空题(每小题3分,共30分)
11.中国一汽公布最新销量数据:2024年1~2月整车销量达44.8万辆,同比增长17.7%,将44.8万用科学记数法表示应为______.
12.在函数中,自变量x的取值范围是______.
13.如图,的对角线AC,BD交于点O,请你添加一个条件______,使成为菱形(填一个即可).
第13题图
14.一只不透明的袋子中放有红、绿、白三种颜色的球各两个,它们除颜色外其他都一样,小明从袋子中摸出一个球后放回摇匀,再摸出一个球,则小明两次都能摸到白球的概率是______.
15.不等式组的解集为,则______.
16.如图,与的边相切,切点为A.将绕点A按顺时针方向旋转得到(点C与点O对应),使点C落在上,边交于点E.若,,则的长为______.
第16题图
17.一个扇形的弧长为,这条弧所对的圆心角为150°,则这个扇形的面积为______.
18.如图,在菱形中,,,对角线,相交于点O,点E在线段上,且,F为线段上的一个动点,则的最小值为______.
第18题图
19.已知等边三角形的边长为4,线段,且.直线与直线交于点E,则的面积为______.
20.如图,在平面直角坐标系中,直线:与x轴交于点B,与y轴交于点A,以x轴为对称轴作直线的轴对称图形直线,点,,,…在直线上,点,,,…在x轴正半轴上,点,,,…在直线上,若,,,…,均为等边三角形,菱形,菱形,菱形……菱形的面积分别是,,,…,,则______.
第20题图
三、解答题(满分60分)
21.(本题满分5分)
先化简,再求值:,其中.
22.(本题满分6分)
如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)画出关于点O成中心对称的;
(2)平移,若点A的对应点的坐标为,画出平移后对应的,求线段在沿直线平移过程中扫过的面积;
(3)若将绕某一点旋转可以得到,则旋转中心的坐标为______.
第22题图
23.(本题满分6分)
如图,抛物线与x轴交于点A,B,与y轴交于点C,连接,,若,.请解答下列问题:
(1)求抛物线的解析式;
(2)点D在第四象限的抛物线上,若,则点D的坐标为______.
第23题图
24.(本题满分7分)
为庆祝“五四”青年节,某中学举行了一场书法比赛.比赛结束后,书法老师随机抽取了部分参赛学生的成绩x(x取整数,满分100分)作为样本,整理并绘制成如图不完整的统计图表。
分数段 频数 频率
30 0.15
m 0.45
60 n
20 0.01
第24题图
请根据以上图表提供的信息,解答下列问题:
(1)表格中______,______,并补全频数分布直方图;
(2)这次抽取的比赛成绩的中位数落在______分数段;
(3)全校共有600名学生参加比赛,请你估计成绩不低于80分的学生人数。
25.(本题满分8分)
在一条笔直的公路上依次有A,B,C三地.甲、乙两车同时出发,甲车从A地匀速行驶到C地,休息1小时后掉头(掉头时间忽略不计),按原路原速返回到A地,乙车从C地匀速行驶到B地,到达B地停止行驶.在两车行驶的过程中,甲、乙两车距各自出发地的路程y(单位:千米)与甲车行驶时间x(单位:小时)之间的函数图象如图所示,请结合图象解决下列问题:
(1)甲车的速度为______千米/时,在图中括号内填入正确的数值;
(2)求乙车从C地到B地的过程中y与x的函数解析式,并直接写出自变量x的取值范围;
(3)在乙车到达B地之前,甲车出发多少小时,甲、乙两车相距150千米?请直接写出答案。
第25题图
26.(本题满分8分)
在中,,,点D,E,F分别在边,,所在直线上,,垂足为G,.
请解答下列问题:
(1)当点F在线段上时,如图①,求证:;
(2)当点F在线段的延长线上时,如图②;当点F在线段的延长线上时,如图③,请直接写出线段,,之间的数量关系,不需要证明
第26题图
27.(本题满分10分)
佳木斯以“16810”打造美丽中国“东极”样板,佳木斯美丽的风景吸引很多市民选购自行车用以骑行.某自行车店计划购进A,B两种型号的公路自行车共50辆,其中每辆B型公路自行车比每辆A型公路自行车多600元,用5000元购进的A型公路自行车与用8000元购进的B型公路自行车数量相同.
(1)求A,B两种型号公路自行车的进货单价;
(2)若该商店计划购进A型公路自行车m辆,计划最多投入68000元,且B型公路自行车的数量不能低于A型公路自行车的数量,求自行车店有几种进货方案?
(3)在(2)的条件下,若A型公路自行车每辆售价为1500元,B型公路自行车每辆售价为2000元、该商店如何进货才能获得最大利润?此时最大利润是多少元?
28.(本题满分10分)
如图,在平面直角坐标系中,矩形的边与x轴重合,与y轴重合,,D是上一点,且,的长是一元二次方程的两个根.
(1)求线段,,的长;
(2)在射线上有一动点P(不与点A,B重合),点P从点A出发,以每秒1个单位长度的速度沿射线方向匀速运动,设运动的时间为t秒,过点P作交射线于点E,交射线于点F,求四边形的面积S与时间t的函数关系式;
(3)在(2)的条件下,在点P运动的过程中,平面内是否存在点Q,使以A,D,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标:若不存在,请说明理由.
第28题图
二○二四年升学模拟大考卷(四)
数学试卷参考答案及评分标准
一、选择题(每小题3分,共30分)
1.B 2.B 3.D 4.D 5.A 6.D 7.B 8.D 9.D 10.D
二、填空题(每小题3分,共30分)
11. 12.且 13.等 14. 15. 16.
17. 18. 19.或 20.
三、解答题(满分60分)
21.(本题满分5分)
解:原式
当时,原式.
22.(本题满分6分)
解:(1)如图,即为所求.
(2)如图,即为所求.(1分)
线段在平移过程中扫过的面积=四边形的面积=四边形的面积.
(3).
23.(本题满分6分)
解:(1)∵,,
∴,.
∴,.∴,.
∴ 解得
∴抛物线的解析式为.
(2).
24.(本题满分7分)
解:(1)90,0.3. 补全频数分布直方图如图所示
(2).
(3)(名).
答:全校600名学生中成绩不低于80分的学生约有240名.
25.(本题满分8分)
解:(1)60,11.
(2)设乙车从C地到B地的过程中y与x的函数解析式为.
(小时)
将代入,得.解得.
∴所求的函数关系式为.
(3)小时或5小时或7小时.
26.(本题满分8分)
解:(1)证明:过点F作,垂足为H,如图①.
∵,∴.
∴,.
∴.
∵,,
∴.∴,.
∵,,∴.
∴.∴.
∴.∴.
∴.
(2)图②:.
图③:.
27.(本题满分10分)
解:(1)设A种型号公路自行车的进货单价是x元,则B种型号公路自行车的进货单价是元.根据题意,得.解得.
经检验是原方程的解,且符合题意.
∴.
答:A种型号公路自行车的进货单价是1000元,B种型号公路自行车的进货单价是1600元.
(2)根据题意,得 解得.
∵m是正整数,∴,21,22,23,24,25.
∴自行车店有六种进货方案,
(3)设该商店利润为W元.根据题意,得
.
∵,∴W随m的增大而增大.
∴当时,W有最大值,.
答:该商店购进A型公路自行车25辆,B型公路自行车25辆能获得最大利润,此时最大利润是22500元.
28.(本题满分10分)
解:(1)∵,的长是一元二次方程的两个根,
∴,.∴
∵四边形为矩形,∴.
∴.
(2)∵,,∴四边形是平行四边形,
在中,.
∴.
∵,∴.∴.
∴平行四边形是矩形.
∵,∴.∴.
∵,∴.
∴.
当时,,∴.∴.
∴;
当时,,同理,得.
∴.
综上,
(3)存在.点或或.
数学试卷
考生注意:
1.考试时间120分钟
2.全卷共三道大题,总分120分
一、选择题(每小题3分,共30分)
1.下列计算正确的是( )
A. B.
C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,则这个几何体的俯视图中看到的小正方形最多有( )
第3题图
A.9个 B.10个 C.11个 D.12个
4.四个数,,,1的平均数、众数、中位数、方差和极差的和为( )
A.3 B.2 C.1 D.0
5.2024龙年春晚主题为“龙行龘龘(dá),欣欣家国”,“龘”这个字引发一波热门关注.据记载,“龘”出自第一部楷书字典《玉篇》,“龙行龘龘”形容龙腾飞的样子,昂扬而热烈.某服装店购进一款印有“龘”字图案的上衣,据店长统计,该款上衣1月份销售量为150件,3月份销售量为216件,则该款上衣销售量的月平均增长率为( )
A.20% B.22% C.25% D.26%
6.若关于x的分式方程的解是负数,则m的取值范围为( )
A. B. C.且 D.且
7.五四青年节前夕,某中学举办歌咏比赛,为鼓励本班同学们积极参加,刘老师打算用48元钱购买甲、乙两种(两种都买)碳素笔作为奖品.已知甲种碳素笔每支6元,乙种碳素笔每支4元,则刘老师购买碳素笔的方案共有( )
A.4种 B.3种 C.2种 D.1种
8.如图,点A在反比例函数的图象上,点B在反比例函数的图象上,轴,交x轴于点C,连接,取的中点D,连接,则(阴影部分)的面积为( )
第8题图
A.3 B.8 C.4 D.2
9.如图,点D在的边上,,,,若,则的长为( )
第9题图
A.2.5 B. C.2 D.3
10.如图,E是矩形的边的中点,于点F,的延长线交于点G,连接,则下列结论:①;②;③若,,则;④;⑤图中相似三角形只有6对.其中正确结论的序号是( )
第10题图
A.①②③ B.②③④ C. ( mailto:A.023%09B.@3%09C.@5 )①④⑤ D.①②③④⑤
二、填空题(每小题3分,共30分)
11.中国一汽公布最新销量数据:2024年1~2月整车销量达44.8万辆,同比增长17.7%,将44.8万用科学记数法表示应为______.
12.在函数中,自变量x的取值范围是______.
13.如图,的对角线AC,BD交于点O,请你添加一个条件______,使成为菱形(填一个即可).
第13题图
14.一只不透明的袋子中放有红、绿、白三种颜色的球各两个,它们除颜色外其他都一样,小明从袋子中摸出一个球后放回摇匀,再摸出一个球,则小明两次都能摸到白球的概率是______.
15.不等式组的解集为,则______.
16.如图,与的边相切,切点为A.将绕点A按顺时针方向旋转得到(点C与点O对应),使点C落在上,边交于点E.若,,则的长为______.
第16题图
17.一个扇形的弧长为,这条弧所对的圆心角为150°,则这个扇形的面积为______.
18.如图,在菱形中,,,对角线,相交于点O,点E在线段上,且,F为线段上的一个动点,则的最小值为______.
第18题图
19.已知等边三角形的边长为4,线段,且.直线与直线交于点E,则的面积为______.
20.如图,在平面直角坐标系中,直线:与x轴交于点B,与y轴交于点A,以x轴为对称轴作直线的轴对称图形直线,点,,,…在直线上,点,,,…在x轴正半轴上,点,,,…在直线上,若,,,…,均为等边三角形,菱形,菱形,菱形……菱形的面积分别是,,,…,,则______.
第20题图
三、解答题(满分60分)
21.(本题满分5分)
先化简,再求值:,其中.
22.(本题满分6分)
如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)画出关于点O成中心对称的;
(2)平移,若点A的对应点的坐标为,画出平移后对应的,求线段在沿直线平移过程中扫过的面积;
(3)若将绕某一点旋转可以得到,则旋转中心的坐标为______.
第22题图
23.(本题满分6分)
如图,抛物线与x轴交于点A,B,与y轴交于点C,连接,,若,.请解答下列问题:
(1)求抛物线的解析式;
(2)点D在第四象限的抛物线上,若,则点D的坐标为______.
第23题图
24.(本题满分7分)
为庆祝“五四”青年节,某中学举行了一场书法比赛.比赛结束后,书法老师随机抽取了部分参赛学生的成绩x(x取整数,满分100分)作为样本,整理并绘制成如图不完整的统计图表。
分数段 频数 频率
30 0.15
m 0.45
60 n
20 0.01
第24题图
请根据以上图表提供的信息,解答下列问题:
(1)表格中______,______,并补全频数分布直方图;
(2)这次抽取的比赛成绩的中位数落在______分数段;
(3)全校共有600名学生参加比赛,请你估计成绩不低于80分的学生人数。
25.(本题满分8分)
在一条笔直的公路上依次有A,B,C三地.甲、乙两车同时出发,甲车从A地匀速行驶到C地,休息1小时后掉头(掉头时间忽略不计),按原路原速返回到A地,乙车从C地匀速行驶到B地,到达B地停止行驶.在两车行驶的过程中,甲、乙两车距各自出发地的路程y(单位:千米)与甲车行驶时间x(单位:小时)之间的函数图象如图所示,请结合图象解决下列问题:
(1)甲车的速度为______千米/时,在图中括号内填入正确的数值;
(2)求乙车从C地到B地的过程中y与x的函数解析式,并直接写出自变量x的取值范围;
(3)在乙车到达B地之前,甲车出发多少小时,甲、乙两车相距150千米?请直接写出答案。
第25题图
26.(本题满分8分)
在中,,,点D,E,F分别在边,,所在直线上,,垂足为G,.
请解答下列问题:
(1)当点F在线段上时,如图①,求证:;
(2)当点F在线段的延长线上时,如图②;当点F在线段的延长线上时,如图③,请直接写出线段,,之间的数量关系,不需要证明
第26题图
27.(本题满分10分)
佳木斯以“16810”打造美丽中国“东极”样板,佳木斯美丽的风景吸引很多市民选购自行车用以骑行.某自行车店计划购进A,B两种型号的公路自行车共50辆,其中每辆B型公路自行车比每辆A型公路自行车多600元,用5000元购进的A型公路自行车与用8000元购进的B型公路自行车数量相同.
(1)求A,B两种型号公路自行车的进货单价;
(2)若该商店计划购进A型公路自行车m辆,计划最多投入68000元,且B型公路自行车的数量不能低于A型公路自行车的数量,求自行车店有几种进货方案?
(3)在(2)的条件下,若A型公路自行车每辆售价为1500元,B型公路自行车每辆售价为2000元、该商店如何进货才能获得最大利润?此时最大利润是多少元?
28.(本题满分10分)
如图,在平面直角坐标系中,矩形的边与x轴重合,与y轴重合,,D是上一点,且,的长是一元二次方程的两个根.
(1)求线段,,的长;
(2)在射线上有一动点P(不与点A,B重合),点P从点A出发,以每秒1个单位长度的速度沿射线方向匀速运动,设运动的时间为t秒,过点P作交射线于点E,交射线于点F,求四边形的面积S与时间t的函数关系式;
(3)在(2)的条件下,在点P运动的过程中,平面内是否存在点Q,使以A,D,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标:若不存在,请说明理由.
第28题图
二○二四年升学模拟大考卷(四)
数学试卷参考答案及评分标准
一、选择题(每小题3分,共30分)
1.B 2.B 3.D 4.D 5.A 6.D 7.B 8.D 9.D 10.D
二、填空题(每小题3分,共30分)
11. 12.且 13.等 14. 15. 16.
17. 18. 19.或 20.
三、解答题(满分60分)
21.(本题满分5分)
解:原式
当时,原式.
22.(本题满分6分)
解:(1)如图,即为所求.
(2)如图,即为所求.(1分)
线段在平移过程中扫过的面积=四边形的面积=四边形的面积.
(3).
23.(本题满分6分)
解:(1)∵,,
∴,.
∴,.∴,.
∴ 解得
∴抛物线的解析式为.
(2).
24.(本题满分7分)
解:(1)90,0.3. 补全频数分布直方图如图所示
(2).
(3)(名).
答:全校600名学生中成绩不低于80分的学生约有240名.
25.(本题满分8分)
解:(1)60,11.
(2)设乙车从C地到B地的过程中y与x的函数解析式为.
(小时)
将代入,得.解得.
∴所求的函数关系式为.
(3)小时或5小时或7小时.
26.(本题满分8分)
解:(1)证明:过点F作,垂足为H,如图①.
∵,∴.
∴,.
∴.
∵,,
∴.∴,.
∵,,∴.
∴.∴.
∴.∴.
∴.
(2)图②:.
图③:.
27.(本题满分10分)
解:(1)设A种型号公路自行车的进货单价是x元,则B种型号公路自行车的进货单价是元.根据题意,得.解得.
经检验是原方程的解,且符合题意.
∴.
答:A种型号公路自行车的进货单价是1000元,B种型号公路自行车的进货单价是1600元.
(2)根据题意,得 解得.
∵m是正整数,∴,21,22,23,24,25.
∴自行车店有六种进货方案,
(3)设该商店利润为W元.根据题意,得
.
∵,∴W随m的增大而增大.
∴当时,W有最大值,.
答:该商店购进A型公路自行车25辆,B型公路自行车25辆能获得最大利润,此时最大利润是22500元.
28.(本题满分10分)
解:(1)∵,的长是一元二次方程的两个根,
∴,.∴
∵四边形为矩形,∴.
∴.
(2)∵,,∴四边形是平行四边形,
在中,.
∴.
∵,∴.∴.
∴平行四边形是矩形.
∵,∴.∴.
∵,∴.
∴.
当时,,∴.∴.
∴;
当时,,同理,得.
∴.
综上,
(3)存在.点或或.
同课章节目录
