2024年黑龙江省齐齐哈尔市铁锋区中考模拟数学试题(含答案)
文档属性
| 名称 | 2024年黑龙江省齐齐哈尔市铁锋区中考模拟数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 900.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 00:00:00 | ||
图片预览



文档简介
初三教学质量监测数学试卷
考生注意:
1.考试时间120分钟.
2.全卷共三道大题,总分120分
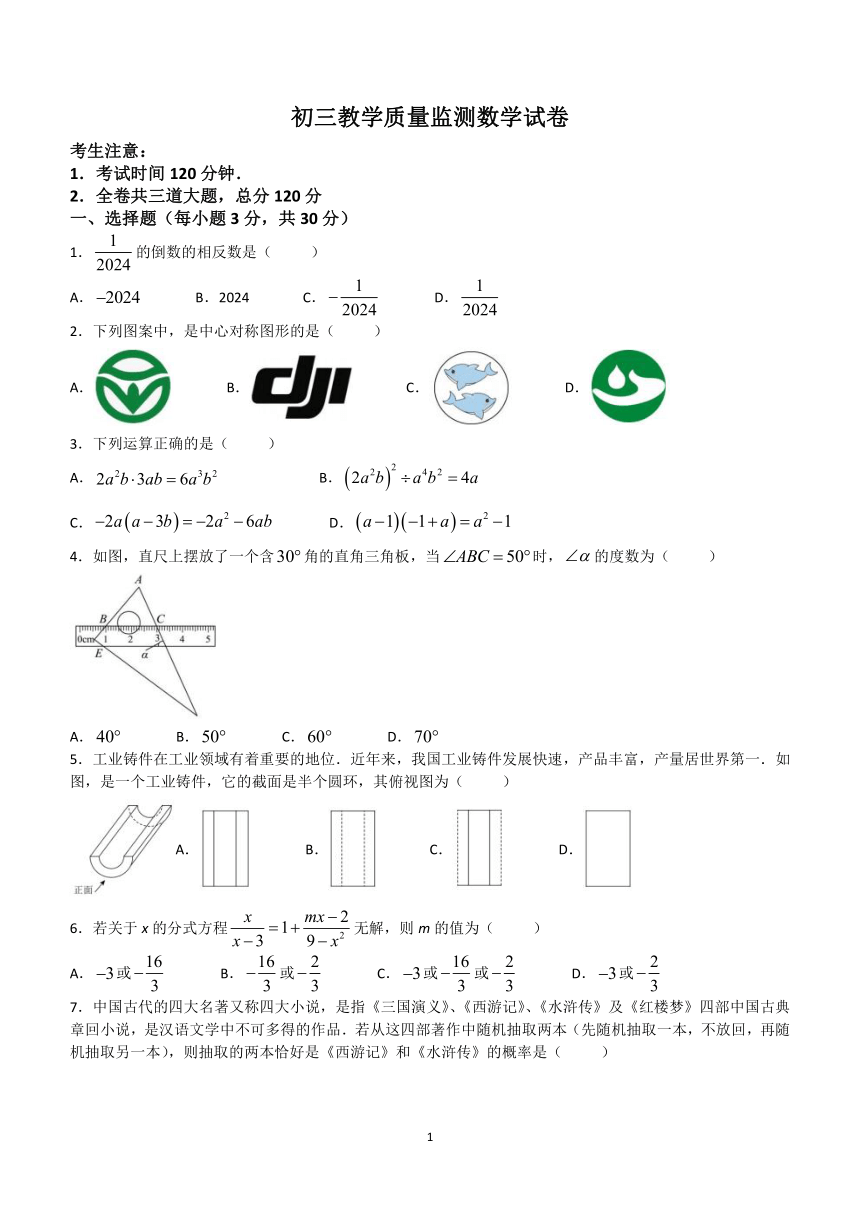
一、选择题(每小题3分,共30分)
1.的倒数的相反数是( )
A. B.2024 C. D.
2.下列图案中,是中心对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.如图,直尺上摆放了一个含角的直角三角板,当时,的度数为( )
A. B. C. D.
5.工业铸件在工业领域有着重要的地位.近年来,我国工业铸件发展快速,产品丰富,产量居世界第一.如图,是一个工业铸件,它的截面是半个圆环,其俯视图为( )
A. B. C. D.
6.若关于x的分式方程无解,则m的值为( )
A.或 B.或 C.或或 D.或
7.中国古代的四大名著又称四大小说,是指《三国演义》、《西游记》、《水浒传》及《红楼梦》四部中国古典章回小说,是汉语文学中不可多得的作品.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《西游记》和《水浒传》的概率是( )
A. B. C. D.
8.如图,已知菱形ABCD的边长为,,点M从点A出发,以的速度向点B运动,点N从点A同时出发,以的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动.则的面积与点M运动的时间t(s)的函数的图象大致是( )
A. B. C. D.
9.某校举行演讲比赛活动,计划拿出180元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件15元,乙种奖品每件10元,则购买方案有( )
A.5种 B.6种 C.7种 D.8种10.
10.如图,已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤ (的实数).其中正确的结论有( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
二、填空题(每小题3分,满分21分)
11.已知1纳米=0.000000001米,则2019纳米用科学记数法表示为_______米.
12.在函数中,自变量x的取值范围是________.
13.若圆锥的主视图为等腰直角三角形,底面半径为1,则圆锥侧面积为_________.
14.如图,长方形纸片ABCD中,点E是CD的中点,连接AE.按以下步骤作图:①分别以点A和点E为圆心,以大于的长为半径作弧,两弧相交于点M和点N.②作直线MN,且直线AMN刚好经过点B.若,则BC的长度是________.
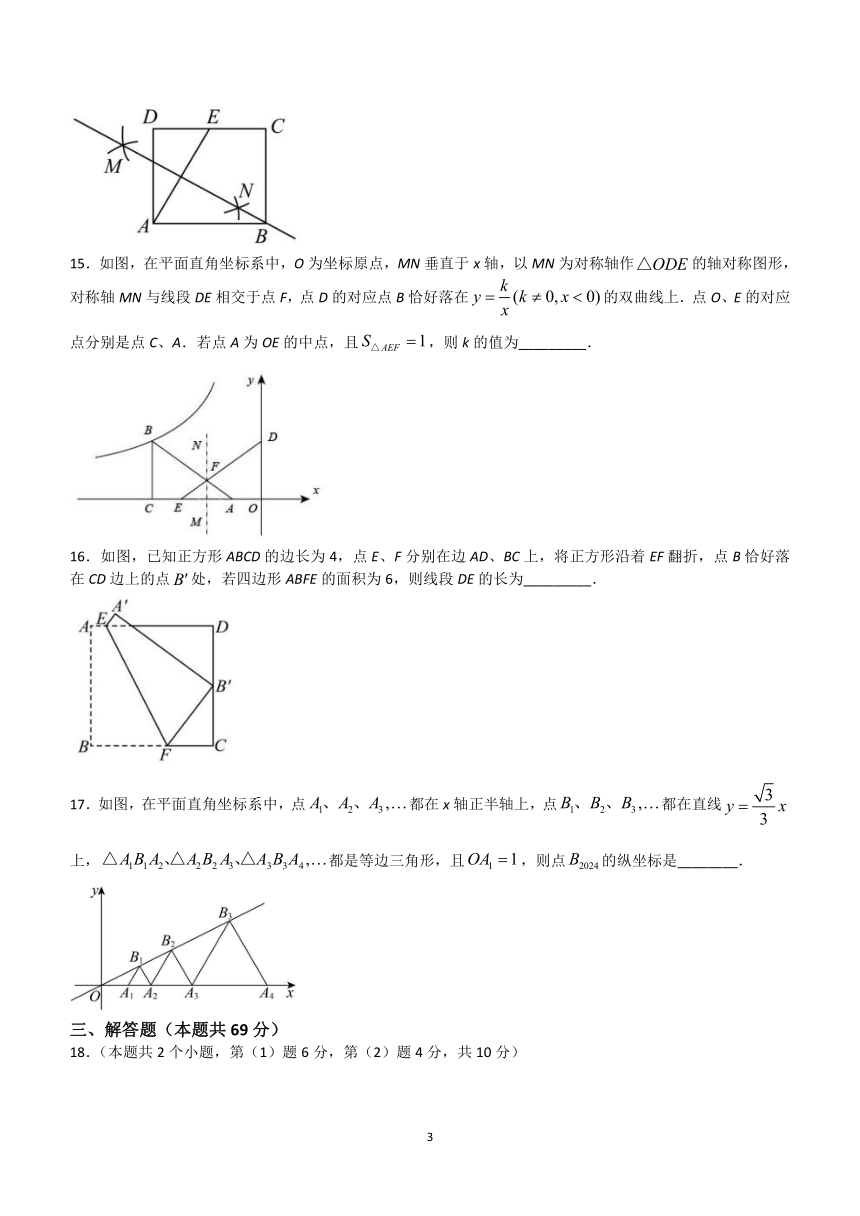
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在的双曲线上.点O、E的对应点分别是点C、A.若点A为OE的中点,且,则k的值为_________.
16.如图,已知正方形ABCD的边长为4,点E、F分别在边AD、BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点处,若四边形ABFE的面积为6,则线段DE的长为_________.
17.如图,在平面直角坐标系中,点都在x轴正半轴上,点都在直线上,都是等边三角形,且,则点的纵坐标是________.
三、解答题(本题共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:
(2)因式分解:
19.(5分)解方程.
20.(8分)
为了解某校八年级学生在语文学习中对小说、诗歌、散文、戏剧四类文学体裁的喜爱情况,随机抽查了部分学生(每人只选一类),然后根据调查数据,绘制了不完整的条形统计图和扇形统计图,结合统计图,解答下列问题.
(1)本次抽样调查的样本容量为_________;
(2)补全条形统计图;
(3)喜爱戏剧的学生对应扇形的圆心角为__________°;
(4)已知该校八年级共有学生800人,请你估计课外活动小组诗歌社团拟招社员200人能否实现,请说明理由.
21.(10分)如图,在中,,D为AB边上的一点,以AD为直径的交BC于点E,交AC于点F,过点C作交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为的切线.
(1)求证:BC是的切线.
(2)若,求四边形CHQE的面积.
22.(10分)在一条笔直的道路上依次有A,B,C三地,男男从A地跑步到C地,同时乐乐从B地跑步到A地,休息1分钟后接到通知,要求乐乐比男男早1分钟到达C地,两人均匀速运动,如图是男男跑步时间t(分钟)与两人距A地路程s(米)之间的函数图象.
(1)________,乐乐去A地的速度为_________;
(2)结合图象,求出乐乐从A地到C地的函数解析式(写出自变量的取值范围);
(3)请直接写出两人距B地的距离相等的时间.
23.综合与实践(12分)
综合与实践折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、飞机、小船等,折纸活动也伴随着我们初中数学的学习.在折纸过程中,既可以得到一些美丽的图形,同时还蕴含着丰富的数学知识.
图① 图② 图③ 图④ 图⑤
如图①,在矩形纸片ABCD中,.
活动一:
(1)如图②,折叠矩形纸片ABCD,使点A落在点C处,点D落在点D处,展开得到折痕EF交AB边于点E,交CD边于点F,则______;
活动二:
(2)如图③,连接图②中的AC交EF于点O,连接AF.猜想四边形AECF是什么特殊四边形,并证明你的猜想;
活动三:,
(3)如图④,折叠矩形纸片ABCD,使点A落在BC边的中点处,点D落在点处,展开得到折痕EF交AB边于点E,交CD边于点F,则______,______;
活动四:
(4)如图⑤,若点A落在靠近点B的BC的四等分点处,即,则与相似吗 若相似,请直接写出相似比;若不相似,请说明理由.
24.综合与探究(14分)
如图,抛物线的对称轴是直线,与x轴交于点A、B两点,且A点的坐标为,与y轴交于点,
(1)求抛物线解析式及顶点D坐标;
(2)点E为抛物线上一点,且,则点E的坐标为______;
(3)点F为线段BC上任意一点,过点F作轴于点M,直线FM交抛物线于点N,求线段FN的最大值;
(4)点P是抛物线对称轴上一点,在平面直角坐标系中是否存在一点Q,使以点A、C、P、Q为顶点的四边形为矩形 若存在,请直接写出点Q的坐标;若不存在,请说明理由.
初三质量监测数学参考答案及评分标准
一、选择题(每题3分、共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A D A C C A A B
二、填空题(每题3分,共21分)
题号 11 12 13 14 15 16 17
答案 且
三、解答题(共69分)
18.计算(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)解:原式. 5分
(2)解: 4分
19.解方程(本题满分5分)
解:,配方,得,
即,∴,
即或,
解得或 5分
20.(本题满分8分)
解:(1)50 1分
(2)补全条形统计图如下:
对四种文学体裁喜爱情况的条形统计图
2分(画出条形图和在条形图上方标注“12”各1分)
(3)36 2分
(4) 2分
∴课外活动小组诗歌社团拟招社员200人不能实现. 1分
21.(本题满分10分)
(1)证明:连接OE,OP,∵,点Q为弦EP的中点,
∴AB垂直平分EP,∴,∵,
∴,∴,
∵BP为的切线,∴,
∴,∴,
∴BC是的切线. ..5分
(2)45 5分
22.(本题满分10分)
解:(1)2:200米/分. 2分(每个1分)
(2)设FG的解析式为
∵
∴,解得
由图象可得乐乐从A地到C地时间t的取值范围为 4分
∴乐乐从A地到C地的函数解析式为 1分
(3)两人距B地的距离相等的时间为分钟或分钟或6分钟 3分
23.综合与实践(本题满分12分)
解:(1) 2分
(2)四边形AECF是菱形. 1分
证明:四边形ABCD是矩形,
∴
∵折叠矩形纸片ABCD,点A落在点C处,折痕为EF,
∴,∵,
在与中,
∴, 2分
∴,∴,
∴四边形AECF是菱形: 1分
(3); 4分(每个2分)
(4)相似,两个三角形的相似比为29:35. 2分(不写“相似”扣一分)
24.解:(1)由题意,得(略)解得 1分
∴解析式为
当时,
∴顶点D的坐标为 1分
(2)或 2分
(3)设直线BC的解析式为
把代入,得 1分
解,得,∴ 1分
设F点的坐标为,则N点的坐标为
∴ 1分
∴当时,线段FN的最大值为 1分
(4)存在, 4分
说明:本套试卷中所有题目,若由其它方法得出正确结论,都可参照本评分标准酌情给分.
考生注意:
1.考试时间120分钟.
2.全卷共三道大题,总分120分
一、选择题(每小题3分,共30分)
1.的倒数的相反数是( )
A. B.2024 C. D.
2.下列图案中,是中心对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.如图,直尺上摆放了一个含角的直角三角板,当时,的度数为( )
A. B. C. D.
5.工业铸件在工业领域有着重要的地位.近年来,我国工业铸件发展快速,产品丰富,产量居世界第一.如图,是一个工业铸件,它的截面是半个圆环,其俯视图为( )
A. B. C. D.
6.若关于x的分式方程无解,则m的值为( )
A.或 B.或 C.或或 D.或
7.中国古代的四大名著又称四大小说,是指《三国演义》、《西游记》、《水浒传》及《红楼梦》四部中国古典章回小说,是汉语文学中不可多得的作品.若从这四部著作中随机抽取两本(先随机抽取一本,不放回,再随机抽取另一本),则抽取的两本恰好是《西游记》和《水浒传》的概率是( )
A. B. C. D.
8.如图,已知菱形ABCD的边长为,,点M从点A出发,以的速度向点B运动,点N从点A同时出发,以的速度经过点D向点C运动,当其中一个动点到达端点时,另一个动点也随之停止运动.则的面积与点M运动的时间t(s)的函数的图象大致是( )
A. B. C. D.
9.某校举行演讲比赛活动,计划拿出180元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件15元,乙种奖品每件10元,则购买方案有( )
A.5种 B.6种 C.7种 D.8种10.
10.如图,已知二次函数的图象如图所示,有下列5个结论:①;②;③;④;⑤ (的实数).其中正确的结论有( )
A.①②③ B.①③④ C.③④⑤ D.②③⑤
二、填空题(每小题3分,满分21分)
11.已知1纳米=0.000000001米,则2019纳米用科学记数法表示为_______米.
12.在函数中,自变量x的取值范围是________.
13.若圆锥的主视图为等腰直角三角形,底面半径为1,则圆锥侧面积为_________.
14.如图,长方形纸片ABCD中,点E是CD的中点,连接AE.按以下步骤作图:①分别以点A和点E为圆心,以大于的长为半径作弧,两弧相交于点M和点N.②作直线MN,且直线AMN刚好经过点B.若,则BC的长度是________.
15.如图,在平面直角坐标系中,O为坐标原点,MN垂直于x轴,以MN为对称轴作的轴对称图形,对称轴MN与线段DE相交于点F,点D的对应点B恰好落在的双曲线上.点O、E的对应点分别是点C、A.若点A为OE的中点,且,则k的值为_________.
16.如图,已知正方形ABCD的边长为4,点E、F分别在边AD、BC上,将正方形沿着EF翻折,点B恰好落在CD边上的点处,若四边形ABFE的面积为6,则线段DE的长为_________.
17.如图,在平面直角坐标系中,点都在x轴正半轴上,点都在直线上,都是等边三角形,且,则点的纵坐标是________.
三、解答题(本题共69分)
18.(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)计算:
(2)因式分解:
19.(5分)解方程.
20.(8分)
为了解某校八年级学生在语文学习中对小说、诗歌、散文、戏剧四类文学体裁的喜爱情况,随机抽查了部分学生(每人只选一类),然后根据调查数据,绘制了不完整的条形统计图和扇形统计图,结合统计图,解答下列问题.
(1)本次抽样调查的样本容量为_________;
(2)补全条形统计图;
(3)喜爱戏剧的学生对应扇形的圆心角为__________°;
(4)已知该校八年级共有学生800人,请你估计课外活动小组诗歌社团拟招社员200人能否实现,请说明理由.
21.(10分)如图,在中,,D为AB边上的一点,以AD为直径的交BC于点E,交AC于点F,过点C作交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为的切线.
(1)求证:BC是的切线.
(2)若,求四边形CHQE的面积.
22.(10分)在一条笔直的道路上依次有A,B,C三地,男男从A地跑步到C地,同时乐乐从B地跑步到A地,休息1分钟后接到通知,要求乐乐比男男早1分钟到达C地,两人均匀速运动,如图是男男跑步时间t(分钟)与两人距A地路程s(米)之间的函数图象.
(1)________,乐乐去A地的速度为_________;
(2)结合图象,求出乐乐从A地到C地的函数解析式(写出自变量的取值范围);
(3)请直接写出两人距B地的距离相等的时间.
23.综合与实践(12分)
综合与实践折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、飞机、小船等,折纸活动也伴随着我们初中数学的学习.在折纸过程中,既可以得到一些美丽的图形,同时还蕴含着丰富的数学知识.
图① 图② 图③ 图④ 图⑤
如图①,在矩形纸片ABCD中,.
活动一:
(1)如图②,折叠矩形纸片ABCD,使点A落在点C处,点D落在点D处,展开得到折痕EF交AB边于点E,交CD边于点F,则______;
活动二:
(2)如图③,连接图②中的AC交EF于点O,连接AF.猜想四边形AECF是什么特殊四边形,并证明你的猜想;
活动三:,
(3)如图④,折叠矩形纸片ABCD,使点A落在BC边的中点处,点D落在点处,展开得到折痕EF交AB边于点E,交CD边于点F,则______,______;
活动四:
(4)如图⑤,若点A落在靠近点B的BC的四等分点处,即,则与相似吗 若相似,请直接写出相似比;若不相似,请说明理由.
24.综合与探究(14分)
如图,抛物线的对称轴是直线,与x轴交于点A、B两点,且A点的坐标为,与y轴交于点,
(1)求抛物线解析式及顶点D坐标;
(2)点E为抛物线上一点,且,则点E的坐标为______;
(3)点F为线段BC上任意一点,过点F作轴于点M,直线FM交抛物线于点N,求线段FN的最大值;
(4)点P是抛物线对称轴上一点,在平面直角坐标系中是否存在一点Q,使以点A、C、P、Q为顶点的四边形为矩形 若存在,请直接写出点Q的坐标;若不存在,请说明理由.
初三质量监测数学参考答案及评分标准
一、选择题(每题3分、共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A D A C C A A B
二、填空题(每题3分,共21分)
题号 11 12 13 14 15 16 17
答案 且
三、解答题(共69分)
18.计算(本题共2个小题,第(1)题6分,第(2)题4分,共10分)
(1)解:原式. 5分
(2)解: 4分
19.解方程(本题满分5分)
解:,配方,得,
即,∴,
即或,
解得或 5分
20.(本题满分8分)
解:(1)50 1分
(2)补全条形统计图如下:
对四种文学体裁喜爱情况的条形统计图
2分(画出条形图和在条形图上方标注“12”各1分)
(3)36 2分
(4) 2分
∴课外活动小组诗歌社团拟招社员200人不能实现. 1分
21.(本题满分10分)
(1)证明:连接OE,OP,∵,点Q为弦EP的中点,
∴AB垂直平分EP,∴,∵,
∴,∴,
∵BP为的切线,∴,
∴,∴,
∴BC是的切线. ..5分
(2)45 5分
22.(本题满分10分)
解:(1)2:200米/分. 2分(每个1分)
(2)设FG的解析式为
∵
∴,解得
由图象可得乐乐从A地到C地时间t的取值范围为 4分
∴乐乐从A地到C地的函数解析式为 1分
(3)两人距B地的距离相等的时间为分钟或分钟或6分钟 3分
23.综合与实践(本题满分12分)
解:(1) 2分
(2)四边形AECF是菱形. 1分
证明:四边形ABCD是矩形,
∴
∵折叠矩形纸片ABCD,点A落在点C处,折痕为EF,
∴,∵,
在与中,
∴, 2分
∴,∴,
∴四边形AECF是菱形: 1分
(3); 4分(每个2分)
(4)相似,两个三角形的相似比为29:35. 2分(不写“相似”扣一分)
24.解:(1)由题意,得(略)解得 1分
∴解析式为
当时,
∴顶点D的坐标为 1分
(2)或 2分
(3)设直线BC的解析式为
把代入,得 1分
解,得,∴ 1分
设F点的坐标为,则N点的坐标为
∴ 1分
∴当时,线段FN的最大值为 1分
(4)存在, 4分
说明:本套试卷中所有题目,若由其它方法得出正确结论,都可参照本评分标准酌情给分.
同课章节目录
