2.5一元一次不等式与一次函数同步练习(含简单答案)北师大版数学八年级下册
文档属性
| 名称 | 2.5一元一次不等式与一次函数同步练习(含简单答案)北师大版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 554.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 15:15:57 | ||
图片预览

文档简介
2.5 一元一次不等式与一次函数
一、单选题
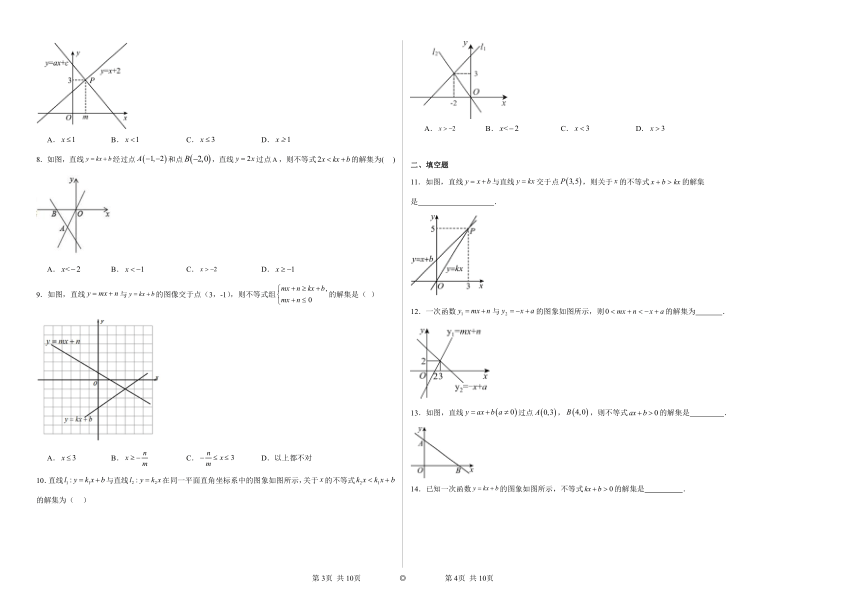
1.如图,一次函数与的图像相交于点,则关于的不等式组的解集为( )
A. B. C. D.无法确定
2.已知直线与直线在第三象限交于点,若直线与轴的交点为,则的取值范围是( )
A. B. C. D.
3.一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
4.如图,直线与的交点的横坐标为,则关于x的不等式的取值范围( )
A. B. C. D.
5.如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
6.一次函数与的图象如图所示,则下列结论:①当时,;②当时,;③当时,,正确的个数为( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线与直线相交于点,则关于x的不等式的解为( )
A. B. C. D.
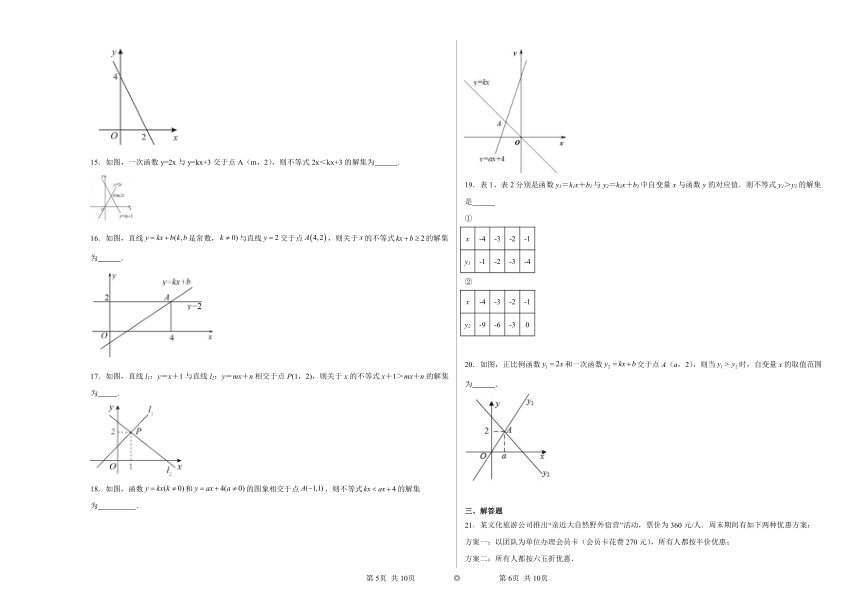
8.如图,直线经过点和点,直线过点,则不等式的解集为( )
A. B. C. D.
9.如图,直线与的图像交于点(3,-1),则不等式组的解集是( )
A. B. C. D.以上都不对
10.直线与直线在同一平面直角坐标系中的图象如图所示,关于的不等式的解集为( )
A. B. C. D.
二、填空题
11.如图,直线与直线交于点,则关于的不等式的解集是 .
12.一次函数与的图象如图所示,则的解集为 .
13.如图,直线过点,,则不等式的解集是 .
14.已知一次函数的图象如图所示,不等式的解集是 .
15.如图,一次函数y=2x与y=kx+3交于点A(m,2),则不等式2x<kx+3的解集为 .
16.如图,直线是常数,与直线交于点,则关于的不等式的解集为 .
17.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,2),则关于x的不等式x+1>mx+n的解集为 .
18.如图,函数和的图象相交于点,则不等式的解集为 .
19.表1、表2分别是函数y1=k1x+b1与y2=k2x+b2中自变量x与函数y的对应值.则不等式y1>y2的解集是
①
x -4 -3 -2 -1
y1 -1 -2 -3 -4
②
x -4 -3 -2 -1
y2 -9 -6 -3 0
20.如图,正比例函数和一次函数交于点A(a,2),则当时,自变量x的取值范围为 .
三、解答题
21.某文化旅游公司推出“亲近大自然野外宿营”活动,票价为360元/人.周末期间有如下两种优惠方案:
方案一:以团队为单位办理会员卡(会员卡花费270元),所有人都按半价优惠;
方案二:所有人都按六五折优惠.
设小明所在的团队有人,在周末期间参加该活动,购票总花费为元.
(1)分别写出这两种方案中关于的函数关系式;
(2)这两种方案中关于的函数图象如图所示,请求出点的坐标,并说明点所表示的实际意义;
(3)当方案一比方案二更优惠时,请直接写出的取值范围.
22.如图,在平面直角坐标系中,直线与直线相交与一点,在轴上的截距为4.
(1)直线,的表达式;
(2)讨论与的大小关系.
23.某水果店经销甲、乙两种水果,两次购进水果的进价相同,购进情况如表所示:
进货批次 甲种水果质量 (单位:千克) 乙种水果质量 (单位:千克) 总费用 (单位:元)
第一次
第二次
(1)求甲、乙两种水果每千克的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共千克,其中进价不变,且投入的资金不超过元,将其中的千克甲种水果和千克乙种水果按进价销售,剩余的甲种水果以每千克元、乙种水果以每千克元的价格销售.若第三次购进的千克水果全部售出后,获得的最大利润不低于元,求正整数的最大值.
24.如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始赢利.该产品的销售量达到多少吨时,生产该产品才能赢利?
25.已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式.
(2)当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
2.B
3.C
4.B
5.D
6.C
7.A
8.B
9.C
10.A
11./
12.
13.
14.
15.x<1
16.
17.x>1
18.
19.x<-2
20.
21.(1), (2) (3)
22.(1):;:
(2)当时,,当时,,当时,.
23.(1)甲种水果每千克的进价为元,乙种水果每千克的进价为元
(2)的最大整数值为
24.当销售量超过时,生产该产品才能赢利
25.(1)
(2)生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,一次函数与的图像相交于点,则关于的不等式组的解集为( )
A. B. C. D.无法确定
2.已知直线与直线在第三象限交于点,若直线与轴的交点为,则的取值范围是( )
A. B. C. D.
3.一次函数的图象如图所示,当时,的取值范围是( )
A. B. C. D.
4.如图,直线与的交点的横坐标为,则关于x的不等式的取值范围( )
A. B. C. D.
5.如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m<kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
6.一次函数与的图象如图所示,则下列结论:①当时,;②当时,;③当时,,正确的个数为( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线与直线相交于点,则关于x的不等式的解为( )
A. B. C. D.
8.如图,直线经过点和点,直线过点,则不等式的解集为( )
A. B. C. D.
9.如图,直线与的图像交于点(3,-1),则不等式组的解集是( )
A. B. C. D.以上都不对
10.直线与直线在同一平面直角坐标系中的图象如图所示,关于的不等式的解集为( )
A. B. C. D.
二、填空题
11.如图,直线与直线交于点,则关于的不等式的解集是 .
12.一次函数与的图象如图所示,则的解集为 .
13.如图,直线过点,,则不等式的解集是 .
14.已知一次函数的图象如图所示,不等式的解集是 .
15.如图,一次函数y=2x与y=kx+3交于点A(m,2),则不等式2x<kx+3的解集为 .
16.如图,直线是常数,与直线交于点,则关于的不等式的解集为 .
17.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,2),则关于x的不等式x+1>mx+n的解集为 .
18.如图,函数和的图象相交于点,则不等式的解集为 .
19.表1、表2分别是函数y1=k1x+b1与y2=k2x+b2中自变量x与函数y的对应值.则不等式y1>y2的解集是
①
x -4 -3 -2 -1
y1 -1 -2 -3 -4
②
x -4 -3 -2 -1
y2 -9 -6 -3 0
20.如图,正比例函数和一次函数交于点A(a,2),则当时,自变量x的取值范围为 .
三、解答题
21.某文化旅游公司推出“亲近大自然野外宿营”活动,票价为360元/人.周末期间有如下两种优惠方案:
方案一:以团队为单位办理会员卡(会员卡花费270元),所有人都按半价优惠;
方案二:所有人都按六五折优惠.
设小明所在的团队有人,在周末期间参加该活动,购票总花费为元.
(1)分别写出这两种方案中关于的函数关系式;
(2)这两种方案中关于的函数图象如图所示,请求出点的坐标,并说明点所表示的实际意义;
(3)当方案一比方案二更优惠时,请直接写出的取值范围.
22.如图,在平面直角坐标系中,直线与直线相交与一点,在轴上的截距为4.
(1)直线,的表达式;
(2)讨论与的大小关系.
23.某水果店经销甲、乙两种水果,两次购进水果的进价相同,购进情况如表所示:
进货批次 甲种水果质量 (单位:千克) 乙种水果质量 (单位:千克) 总费用 (单位:元)
第一次
第二次
(1)求甲、乙两种水果每千克的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共千克,其中进价不变,且投入的资金不超过元,将其中的千克甲种水果和千克乙种水果按进价销售,剩余的甲种水果以每千克元、乙种水果以每千克元的价格销售.若第三次购进的千克水果全部售出后,获得的最大利润不低于元,求正整数的最大值.
24.如图,反映了某产品的销售收入与销售量之间的关系,反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始赢利.该产品的销售量达到多少吨时,生产该产品才能赢利?
25.已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式.
(2)当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
2.B
3.C
4.B
5.D
6.C
7.A
8.B
9.C
10.A
11./
12.
13.
14.
15.x<1
16.
17.x>1
18.
19.x<-2
20.
21.(1), (2) (3)
22.(1):;:
(2)当时,,当时,,当时,.
23.(1)甲种水果每千克的进价为元,乙种水果每千克的进价为元
(2)的最大整数值为
24.当销售量超过时,生产该产品才能赢利
25.(1)
(2)生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
