浙江省杭州学军中学2023-2024学年高二下学期6月月考数学试题(PDF版无答案)
文档属性
| 名称 | 浙江省杭州学军中学2023-2024学年高二下学期6月月考数学试题(PDF版无答案) | 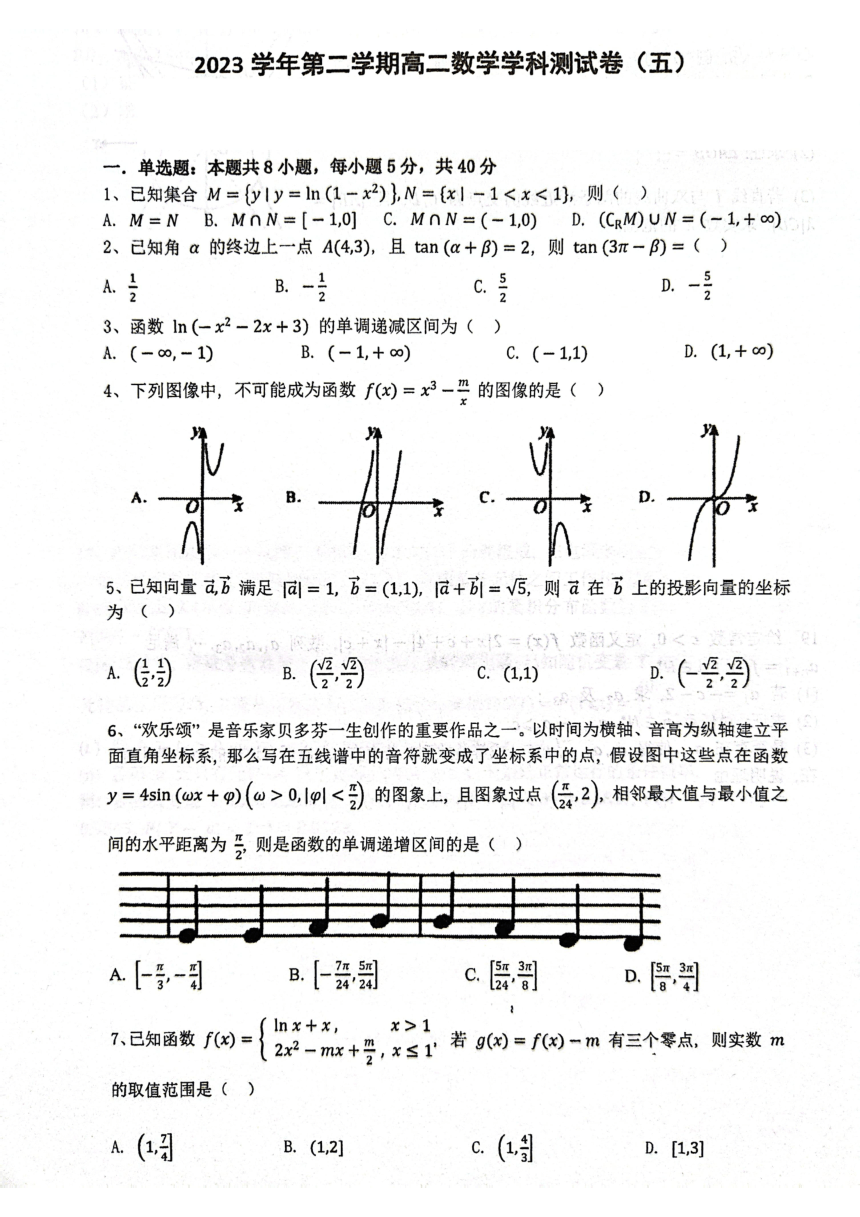 | |
| 格式 | |||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 14:43:00 | ||
图片预览


文档简介
2023学年第二学期高二数学学科测试卷(五)
一.单选题:本题共8小题,每小题5分,共40分
1、已知集合M={y1y=ln(1-x2)}N=(x1-1A.M=NB.MnN=[-1,0]C.MnN=(-1,0)D.(CRM)UN=(-1,+∞)
2、己知角a的终边上一点A(4,3),且tan(a+β)=2,则tan(3π-β)=()
k月
B-分
c
D.-
3、函数1n(-x2-2x+3)的单调递减区间为()
A.(-∞,-1)
B.(-1,+∞)
C.(-1,1)
D.(1,+o)
4、下列图像中,不可能成为函数f(x)=x3-”的图像的是()
5、已知向量,方满足@=1,方=(1,1),+=V5,则a在上的投影向量的坐标
为()
x)n爱9及0<
A(引
B.
C.(1,1)
D.(
6、“欢乐颂”是音乐家贝多芬一生创作的重要作品之一。以时间为横轴、音高为纵轴建立平
面直角坐标系,那么写在五线谱中的音符就变成了坐标系中的点,假设图中这些点在函数
y=4sin(wx+p)(w>0,lpl<》的图象上,且图象过点(经2),相邻最大值与最小值之
间的水平距离为?则是函数的单调递增区间的是()
A[,-割
B【别
c既剖
D悟剖
22-mx+受,xs1若g6)=f()-m有三个零点,则实数m
Inx+x,
7、已知函数f(x)=
龙>1
的取值范围是()
(1,到
B.(1,2]
c.(1剑
D.[1,3]
8、张衡是中国东汉时期伟大的天文学家、数学家,他曾在数学著作《算罔论》中得出结论:
圆周率的平方除以十六约等于八分之五.已知在菱形ABCD中,AB=BD=2V3,将
△ABD沿BD进行翻折,使得AC=2V6.那么三梭锥A一BCD外接球表面积约为(,)
A.72
B.24V10
C.28V10
D.3210
二,多选题:本题共3小题,每小题6分,共18分,在每小题给出的选项中有多项符合题
目要求,全部选对得6分,部分选对得3分,有选错的得0分.
9、在△ABC中,D为边AC上的一点,且满足AD=DC,若P为边BD上的一点,
且满足AP=mAB+nAC(m>0,n>0),则下列结论正确的是()
A.m+2n=1
B.mn的最大值为合
C4+三的最小值为6+4V2
D.m2+9n2的最小值为
10、对于数列{an,若存在正数M,使得对一切正整数n,都有Ian|≤M,则称数列
{amJ是有界的.若这样的正数M不存在,则称数列{an}是无界的.记数列{an}的前
n项和为Sn,下列结论正确的是()
…
A.若a=是
则数列a}是无界的B.若a=(份”sinn则数列5)是有界的
.A04)i
从:
C.若a=(-1)”,则数列S}是有界的D,若am=2+则数列Sd是有界的
11、已知函数f()及其导函数f'(x)的定义域均为R,若f()是奇函数,f(2)=-f1)≠0,
且对任意xyER,f(x+y)=f(xfy)+f'()fy),则()3
Af'()=克B.f9)=0C.29f=1AD.f'(=-1
司:
三.填空题:本题共3小题,每小题5分,共15分.
089220
12、已知复数z满足z=(1+2i)(1+)(其中i为虚数单位),则z=
13、学校一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,
则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为
(用数字作答)
14、已知⊙01:x2+y-2)2=1,⊙02:(x-3)2+(0y-6)2=9,过x轴上一点P分别
作两圆的切线,切点分别是M,N,求IPM+PW|的最小值为
四.解答题:本题共5小题,共77分,其中第15题13分,第16题和第17题每题15分,
第18题和第19题每题17分,解答题应写出文字说明、证明过程或演算步骤
15、已知△ABC的角A,B,C的对边分别为a,b,c,且sinA(ccos B+bcos C)-csin B=
csin C+bsin B
(1)求角A;
(2)若AD平分∠BAC交线段BC于点D,且AD=2,BD=2CD,求△ABC的周长.
一.单选题:本题共8小题,每小题5分,共40分
1、已知集合M={y1y=ln(1-x2)}N=(x1-1
2、己知角a的终边上一点A(4,3),且tan(a+β)=2,则tan(3π-β)=()
k月
B-分
c
D.-
3、函数1n(-x2-2x+3)的单调递减区间为()
A.(-∞,-1)
B.(-1,+∞)
C.(-1,1)
D.(1,+o)
4、下列图像中,不可能成为函数f(x)=x3-”的图像的是()
5、已知向量,方满足@=1,方=(1,1),+=V5,则a在上的投影向量的坐标
为()
x)n爱9及0<
A(引
B.
C.(1,1)
D.(
6、“欢乐颂”是音乐家贝多芬一生创作的重要作品之一。以时间为横轴、音高为纵轴建立平
面直角坐标系,那么写在五线谱中的音符就变成了坐标系中的点,假设图中这些点在函数
y=4sin(wx+p)(w>0,lpl<》的图象上,且图象过点(经2),相邻最大值与最小值之
间的水平距离为?则是函数的单调递增区间的是()
A[,-割
B【别
c既剖
D悟剖
22-mx+受,xs1若g6)=f()-m有三个零点,则实数m
Inx+x,
7、已知函数f(x)=
龙>1
的取值范围是()
(1,到
B.(1,2]
c.(1剑
D.[1,3]
8、张衡是中国东汉时期伟大的天文学家、数学家,他曾在数学著作《算罔论》中得出结论:
圆周率的平方除以十六约等于八分之五.已知在菱形ABCD中,AB=BD=2V3,将
△ABD沿BD进行翻折,使得AC=2V6.那么三梭锥A一BCD外接球表面积约为(,)
A.72
B.24V10
C.28V10
D.3210
二,多选题:本题共3小题,每小题6分,共18分,在每小题给出的选项中有多项符合题
目要求,全部选对得6分,部分选对得3分,有选错的得0分.
9、在△ABC中,D为边AC上的一点,且满足AD=DC,若P为边BD上的一点,
且满足AP=mAB+nAC(m>0,n>0),则下列结论正确的是()
A.m+2n=1
B.mn的最大值为合
C4+三的最小值为6+4V2
D.m2+9n2的最小值为
10、对于数列{an,若存在正数M,使得对一切正整数n,都有Ian|≤M,则称数列
{amJ是有界的.若这样的正数M不存在,则称数列{an}是无界的.记数列{an}的前
n项和为Sn,下列结论正确的是()
…
A.若a=是
则数列a}是无界的B.若a=(份”sinn则数列5)是有界的
.A04)i
从:
C.若a=(-1)”,则数列S}是有界的D,若am=2+则数列Sd是有界的
11、已知函数f()及其导函数f'(x)的定义域均为R,若f()是奇函数,f(2)=-f1)≠0,
且对任意xyER,f(x+y)=f(xfy)+f'()fy),则()3
Af'()=克B.f9)=0C.29f=1AD.f'(=-1
司:
三.填空题:本题共3小题,每小题5分,共15分.
089220
12、已知复数z满足z=(1+2i)(1+)(其中i为虚数单位),则z=
13、学校一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,
则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为
(用数字作答)
14、已知⊙01:x2+y-2)2=1,⊙02:(x-3)2+(0y-6)2=9,过x轴上一点P分别
作两圆的切线,切点分别是M,N,求IPM+PW|的最小值为
四.解答题:本题共5小题,共77分,其中第15题13分,第16题和第17题每题15分,
第18题和第19题每题17分,解答题应写出文字说明、证明过程或演算步骤
15、已知△ABC的角A,B,C的对边分别为a,b,c,且sinA(ccos B+bcos C)-csin B=
csin C+bsin B
(1)求角A;
(2)若AD平分∠BAC交线段BC于点D,且AD=2,BD=2CD,求△ABC的周长.
同课章节目录
