人教版八年级数学上册试题 11.2 与三角形有关的角同步练习(含解析)
文档属性
| 名称 | 人教版八年级数学上册试题 11.2 与三角形有关的角同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 16:37:10 | ||
图片预览




文档简介
11.2 与三角形有关的角
一、单选题
1.如图,直线,将三角尺直角顶点放在直线b上,若,则的度数是( )
A. B. C. D.
2.如图,、是的角平分线,并且、交于点,若,则等于( )
A. B. C. D.
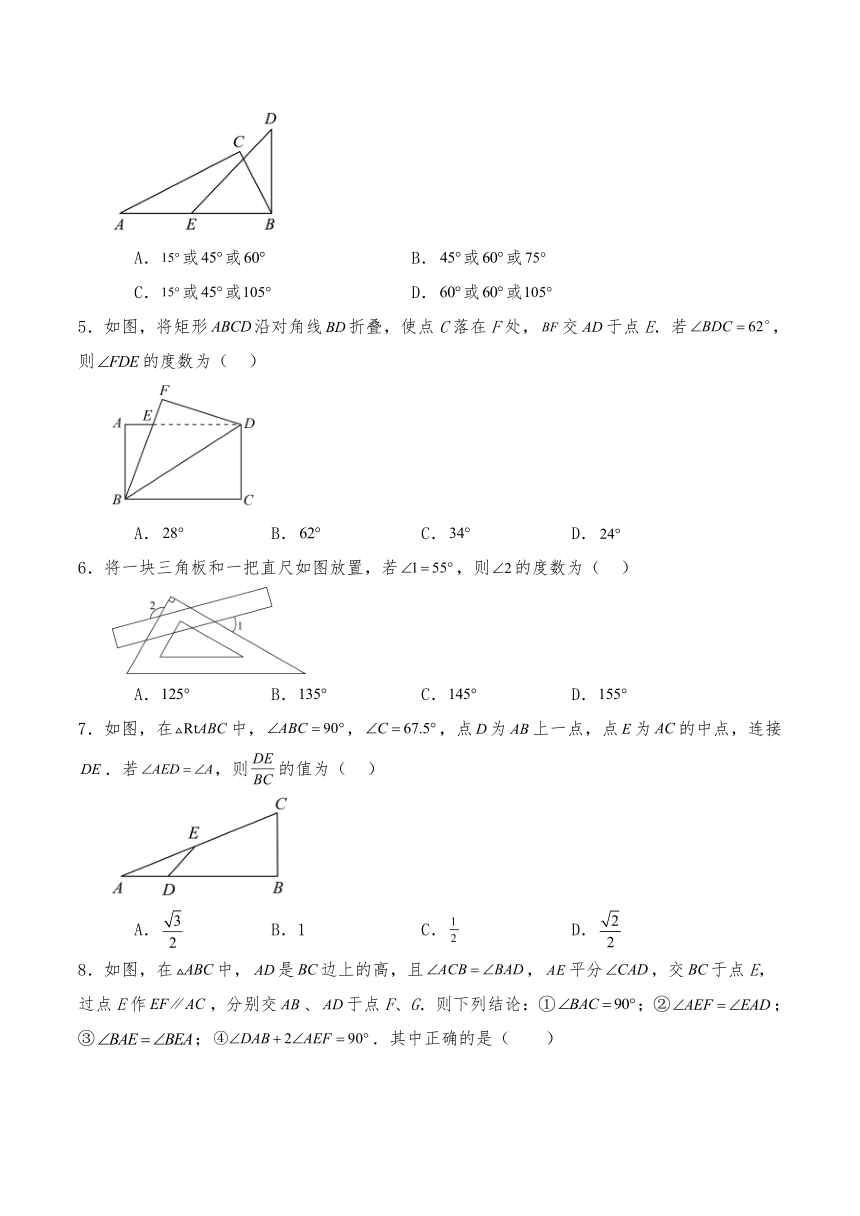
3.如图,在中,点D、点E分别在边、上一点,将和分别沿和折叠至.已知且,则为( )
A. B. C. D.
4.如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
5.如图,将矩形沿对角线折叠,使点C落在F处,交于点E.若,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺如图放置,若,则的度数为( )
A. B. C. D.
7.如图,在中,,,点为上一点,点为的中点,连接.若,则的值为( )
A. B.1 C. D.
8.如图,在中,是边上的高,且,平分,交于点E,过点E作,分别交、于点F、G.则下列结论:①;②;③;.其中正确的是( )
A.②③ B.①③④ C.①②④ D.①②③④
9.如图,,,,点,,在同一直线上,若,,则的度数是( )
A. B. C. D.
10.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,已知,与交于点,于点,若,则______.
12.如图,,则__________度.
13.如图,在中,,三角形两外角的角平分线交于点E,则________.
14.如图,∠1,∠2,∠3的大小关系是_____.
15.如图,在中,点O是和的平分线的交点,点D是延长线上的点,和的平分线交于点E,,则的度数为_________.(用含的式子表示)
16.如图,在中,D是上一点,,将沿着翻折得到,则______.
17.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
18.如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则____________.
三、解答题
19.用两种不同的方法证明“三角形的内角和等于”.
20.如图,直线,被直线,所截, ,,垂足为.直线平分交于点.点在直线上,,.
(1)试说明:;
(2)求的度数.
21.如图,已知,.
(1) 求证:;
(2) 连接,若,,,则___________.
22.已知,在中,点E在边上,点D是上一个动点,将沿E、D所在直线进行翻折得到.
(1) 如图,若,则______;
(2) 在图中细心的小明发现了,,之间的关系,请您替小明写出这个数量关系并证明.
23.如图,在中,,交的延长线于D,于E,
(1) 如图1,若,,求的度数;
(2) 如图2,若平分,交的延长线于F,直接写出与相等的角(除外).
24.在中,平分交于点,点是线段上的动点(不与点重合),过点作交射线于点,的平分线所在直线与射线交于点.
(1) 如图,点在线段上运动.
① 若,,则的度数是 ;的度数是 ,
② 探究与之间的数量关系,并说明理由;
(2) 若点在线段上运动时,请直接写出与之间的数量关系.
答案
一、单选题
1.C
【分析】根据平行线的性质可得,再利用三角形的内角和定理可求,最后根据对顶角相等即可求出结果.
解:如图,∵,,
∴,
又∵,
∴,
∴,
故选:C.
2.B
【分析】由,可得,再根据、是的角平分线,即可得到的度数,最后根据三角形内角和定理,即可得到的度数.
解:,
∴,
又、是的角平分线,
,
.
故选:B.
3.B
【分析】设,则,设,由翻折可知,,再根据三角形的内角和定理,即可得出结果.
解:设,则,设,
由翻折可知,,,
,,
由,得,
在中,,
,
解得:,
在中,,
解得:
由得,
在中,,
.
故选:B.
4.C
【分析】分三种情况讨论:①当时;②当时;③当时,利平行线的性质和三角形内角和定理分别求解,即可得到答案.
解:由三角板的性质可知,,,,,
分三种情况讨论:
①如图1,当时,与交于点F,
,
,
;
②如图2,当时,
;
③如图3,当时,
,
;
综上可知,的度数为或或,
故选C.
5.C
【分析】由题意可得,,从而利用直角三角形的两个锐角互余可得,再利用平行线的性质可得,然后利用折叠的性质可得,从而利用角的和差关系,进行计算即可解答.
解:由题意可得,,
∵,
∴,
∵,
∴,
由折叠得:,
∴,
故选:C.
6.C
【分析】根据平行线的性质,可得,再由对顶角相等可得,从而得到,即可求解.
解:如图,
根据题意得:,
∴,
∴,
∴,
∴.
故选:C.
7.D
【分析】过点作于点,由已知可得的中位线,则,再由直角三角形的性质求得,由及三角形外角的性质求得,进而求得,即可求解.
解:如图,连接,过点作于点,
,点为的中点,
,
,
,
,
点是的中点,
是的中位线,
,
在中,,,
,
,
,
,
,
故选:D.
8.D
【分析】证明即可判断①正确;利用三角形的外角的性质,角的和差定义即可判断③正确;根据,结合角平分线的定义即可判断②,证明即可判断④正确.
解:,
,
,
,
,
,故①正确,
平分,
,
,,
,故③正确,
,
,
,
,,故②正确;
,,
,
,
,故④正确,
正确的有:①②③④,故D正确.
故选:D.
9.C
【分析】由可证得,继而证明,由全等三角形对应角相等得到,最后由三角形的外角性质解答即可.
解:
,,
,
故选:C.
10.D
二、填空题
11.140°
【分析】首先根据对顶角相等即可求出∠CED的度数,再根据三角形的内角和即可求得∠ECD的度数,根据平行线的性质即可求出∠CAB的度数,再根据补角的性质即可求解;
解:∵ ∠1=50°,
∴∠CED=50°,
∵ 三角形内角和为180°,BD⊥CD,
∴∠ECD=180°-90°-50°=40°,
∵ AB∥CD,
∴∠EAB=40°,
∴∠2=180°-40°=140°,
故答案为:140°.
12.50
【分析】利用两直线平行,同位角相等和三角形内角和定理计算即可.
解:∵,
,
.
故答案为:50.
13.61°
【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.
解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,
∴∠BAC+∠BCA=180°﹣∠B=180°﹣58°=122°,
∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,
∴∠DAC+∠ACF=360°﹣(∠BAC+∠BCA)=360°﹣122°=238°,
∵AE平分∠DAC,CE平分∠ACF,
∴∠EAC=∠DAC,∠ECA=∠ACF,
∴∠EAC+∠ECA =(∠DAC+∠ACF)=119°,
∵∠EAC+∠ECA+∠AEC=180°,
∴∠AEC=180°﹣(∠EAC+∠ECA)=180°﹣119°=61°,
故答案为:61°.
14.∠1<∠2<∠3
【分析】根据三角形外角的性质判断出∠1与∠2的大小,再判断出∠2与∠3的大小即可.
解:如图,∵∠2是△ABD的外角,∴∠2>∠1,
同理,∵∠3是△BCD的外角,∴∠3>∠2,
∴∠1<∠2<∠3.
故答案为∠1<∠2<∠3.
15./
【分析】在中,先根据点O是和的平分线的交点,,所以,因为和的平分线交于点E,,,在中,,化简即可用含的式子表示的度数.
解:∵点O是和的平分线的交点,
∴,
∵和的平分线交于点E,
∴,,
在中,,
即,
故答案为:.
16.
【分析】根据三角形内角和、三角形外角的性质和翻折的性质解答即可.
解:∵,
∴,
∴,
∴,
∵将沿着翻折得到,
∴,
∴,
故答案为:.
17.130°
【分析】由三角形的外角性质可得∠BAC+∠ABC=100°,再由角平分线的定义得∠1∠BAC,∠3∠ABC,从而可求得∠1+∠3=50°,再利用三角形的内角和定理即可求解.
解:∵∠ACQ是△ABC的外角,且∠ACQ=100°,
∴∠BAC+∠ABC=100°,
∵AD平分∠BAC,BD平分∠ABC,
∴∠1∠BAC,∠3∠ABC,
∴∠1+∠3(∠BAC+∠ABC)=50°,
∴∠D=180°﹣(∠1+∠3)=130°.
故答案为:130°.
18.10°
【分析】在△EFD中,由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,所以∠B+∠BAC+∠EDH=90°;联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EDH=(∠C-∠B).
解:由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,
故∠B+∠BAC+∠EDH=90° ①,
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠C+∠B+∠BAC=90° ②,
②-①,得:∠EDH=(∠C-∠B)=×(50°-30°)=10°.
故答案为:10°.
三、解答题
19.
解:①将一个三角形的三个角分别往内折,三个角刚好组成一平角,所以为180度.
②在一个顶点作它对边的平行线,用内错角证明.
证明:,,
∴.
20.
(1)解:因为,
所以,
所以
,
因为,
所以,
因为平分,
所以,
所以
,
所以.
(2)解:由(1)得
.
21.
解:(1)证明:,,
,
,
,
,
,
;
(2)解:,,
,
,,
,
,
,
,
故答案为:80.
22.
解:(1)在中,,
∴.
由折叠的性质,可知:,,
∴.
又∵∠,
∴
.
故答案为:;
(2).
证明:在中,,
∴.
由折叠的性质,可知:,
∴.
又∵,
∴
,
即.
23.
(1)解:,,
,
,,
,
.
(2)解:平分,
,
,,
,
,
,
,
,
同理可得,
.
24.
(1)解:①∵,,
∴在中,,
∵,
∴,
∵平分,
∴,
∴,
故答案为:;
②∵是是一个外角,
∴,
∵,
∴,
∵,
∴,
∵平分,平分,
∴,,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵是的平分线,
∴,
∴,
∴,
∵平分,
∴,
∴,
一、单选题
1.如图,直线,将三角尺直角顶点放在直线b上,若,则的度数是( )
A. B. C. D.
2.如图,、是的角平分线,并且、交于点,若,则等于( )
A. B. C. D.
3.如图,在中,点D、点E分别在边、上一点,将和分别沿和折叠至.已知且,则为( )
A. B. C. D.
4.如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A.或或 B.或或
C.或或 D.或或
5.如图,将矩形沿对角线折叠,使点C落在F处,交于点E.若,则的度数为( )
A. B. C. D.
6.将一块三角板和一把直尺如图放置,若,则的度数为( )
A. B. C. D.
7.如图,在中,,,点为上一点,点为的中点,连接.若,则的值为( )
A. B.1 C. D.
8.如图,在中,是边上的高,且,平分,交于点E,过点E作,分别交、于点F、G.则下列结论:①;②;③;.其中正确的是( )
A.②③ B.①③④ C.①②④ D.①②③④
9.如图,,,,点,,在同一直线上,若,,则的度数是( )
A. B. C. D.
10.如图,,将一副直角三角板作如下摆放,,.下列结论:①;②;③;④.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.如图,已知,与交于点,于点,若,则______.
12.如图,,则__________度.
13.如图,在中,,三角形两外角的角平分线交于点E,则________.
14.如图,∠1,∠2,∠3的大小关系是_____.
15.如图,在中,点O是和的平分线的交点,点D是延长线上的点,和的平分线交于点E,,则的度数为_________.(用含的式子表示)
16.如图,在中,D是上一点,,将沿着翻折得到,则______.
17.三角形的一个外角是100°,则与它不相邻的两内角平分线夹角(钝角)是 _____.
18.如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则____________.
三、解答题
19.用两种不同的方法证明“三角形的内角和等于”.
20.如图,直线,被直线,所截, ,,垂足为.直线平分交于点.点在直线上,,.
(1)试说明:;
(2)求的度数.
21.如图,已知,.
(1) 求证:;
(2) 连接,若,,,则___________.
22.已知,在中,点E在边上,点D是上一个动点,将沿E、D所在直线进行翻折得到.
(1) 如图,若,则______;
(2) 在图中细心的小明发现了,,之间的关系,请您替小明写出这个数量关系并证明.
23.如图,在中,,交的延长线于D,于E,
(1) 如图1,若,,求的度数;
(2) 如图2,若平分,交的延长线于F,直接写出与相等的角(除外).
24.在中,平分交于点,点是线段上的动点(不与点重合),过点作交射线于点,的平分线所在直线与射线交于点.
(1) 如图,点在线段上运动.
① 若,,则的度数是 ;的度数是 ,
② 探究与之间的数量关系,并说明理由;
(2) 若点在线段上运动时,请直接写出与之间的数量关系.
答案
一、单选题
1.C
【分析】根据平行线的性质可得,再利用三角形的内角和定理可求,最后根据对顶角相等即可求出结果.
解:如图,∵,,
∴,
又∵,
∴,
∴,
故选:C.
2.B
【分析】由,可得,再根据、是的角平分线,即可得到的度数,最后根据三角形内角和定理,即可得到的度数.
解:,
∴,
又、是的角平分线,
,
.
故选:B.
3.B
【分析】设,则,设,由翻折可知,,再根据三角形的内角和定理,即可得出结果.
解:设,则,设,
由翻折可知,,,
,,
由,得,
在中,,
,
解得:,
在中,,
解得:
由得,
在中,,
.
故选:B.
4.C
【分析】分三种情况讨论:①当时;②当时;③当时,利平行线的性质和三角形内角和定理分别求解,即可得到答案.
解:由三角板的性质可知,,,,,
分三种情况讨论:
①如图1,当时,与交于点F,
,
,
;
②如图2,当时,
;
③如图3,当时,
,
;
综上可知,的度数为或或,
故选C.
5.C
【分析】由题意可得,,从而利用直角三角形的两个锐角互余可得,再利用平行线的性质可得,然后利用折叠的性质可得,从而利用角的和差关系,进行计算即可解答.
解:由题意可得,,
∵,
∴,
∵,
∴,
由折叠得:,
∴,
故选:C.
6.C
【分析】根据平行线的性质,可得,再由对顶角相等可得,从而得到,即可求解.
解:如图,
根据题意得:,
∴,
∴,
∴,
∴.
故选:C.
7.D
【分析】过点作于点,由已知可得的中位线,则,再由直角三角形的性质求得,由及三角形外角的性质求得,进而求得,即可求解.
解:如图,连接,过点作于点,
,点为的中点,
,
,
,
,
点是的中点,
是的中位线,
,
在中,,,
,
,
,
,
,
故选:D.
8.D
【分析】证明即可判断①正确;利用三角形的外角的性质,角的和差定义即可判断③正确;根据,结合角平分线的定义即可判断②,证明即可判断④正确.
解:,
,
,
,
,
,故①正确,
平分,
,
,,
,故③正确,
,
,
,
,,故②正确;
,,
,
,
,故④正确,
正确的有:①②③④,故D正确.
故选:D.
9.C
【分析】由可证得,继而证明,由全等三角形对应角相等得到,最后由三角形的外角性质解答即可.
解:
,,
,
故选:C.
10.D
二、填空题
11.140°
【分析】首先根据对顶角相等即可求出∠CED的度数,再根据三角形的内角和即可求得∠ECD的度数,根据平行线的性质即可求出∠CAB的度数,再根据补角的性质即可求解;
解:∵ ∠1=50°,
∴∠CED=50°,
∵ 三角形内角和为180°,BD⊥CD,
∴∠ECD=180°-90°-50°=40°,
∵ AB∥CD,
∴∠EAB=40°,
∴∠2=180°-40°=140°,
故答案为:140°.
12.50
【分析】利用两直线平行,同位角相等和三角形内角和定理计算即可.
解:∵,
,
.
故答案为:50.
13.61°
【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.
解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,
∴∠BAC+∠BCA=180°﹣∠B=180°﹣58°=122°,
∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,
∴∠DAC+∠ACF=360°﹣(∠BAC+∠BCA)=360°﹣122°=238°,
∵AE平分∠DAC,CE平分∠ACF,
∴∠EAC=∠DAC,∠ECA=∠ACF,
∴∠EAC+∠ECA =(∠DAC+∠ACF)=119°,
∵∠EAC+∠ECA+∠AEC=180°,
∴∠AEC=180°﹣(∠EAC+∠ECA)=180°﹣119°=61°,
故答案为:61°.
14.∠1<∠2<∠3
【分析】根据三角形外角的性质判断出∠1与∠2的大小,再判断出∠2与∠3的大小即可.
解:如图,∵∠2是△ABD的外角,∴∠2>∠1,
同理,∵∠3是△BCD的外角,∴∠3>∠2,
∴∠1<∠2<∠3.
故答案为∠1<∠2<∠3.
15./
【分析】在中,先根据点O是和的平分线的交点,,所以,因为和的平分线交于点E,,,在中,,化简即可用含的式子表示的度数.
解:∵点O是和的平分线的交点,
∴,
∵和的平分线交于点E,
∴,,
在中,,
即,
故答案为:.
16.
【分析】根据三角形内角和、三角形外角的性质和翻折的性质解答即可.
解:∵,
∴,
∴,
∴,
∵将沿着翻折得到,
∴,
∴,
故答案为:.
17.130°
【分析】由三角形的外角性质可得∠BAC+∠ABC=100°,再由角平分线的定义得∠1∠BAC,∠3∠ABC,从而可求得∠1+∠3=50°,再利用三角形的内角和定理即可求解.
解:∵∠ACQ是△ABC的外角,且∠ACQ=100°,
∴∠BAC+∠ABC=100°,
∵AD平分∠BAC,BD平分∠ABC,
∴∠1∠BAC,∠3∠ABC,
∴∠1+∠3(∠BAC+∠ABC)=50°,
∴∠D=180°﹣(∠1+∠3)=130°.
故答案为:130°.
18.10°
【分析】在△EFD中,由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,所以∠B+∠BAC+∠EDH=90°;联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EDH=(∠C-∠B).
解:由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,
故∠B+∠BAC+∠EDH=90° ①,
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠C+∠B+∠BAC=90° ②,
②-①,得:∠EDH=(∠C-∠B)=×(50°-30°)=10°.
故答案为:10°.
三、解答题
19.
解:①将一个三角形的三个角分别往内折,三个角刚好组成一平角,所以为180度.
②在一个顶点作它对边的平行线,用内错角证明.
证明:,,
∴.
20.
(1)解:因为,
所以,
所以
,
因为,
所以,
因为平分,
所以,
所以
,
所以.
(2)解:由(1)得
.
21.
解:(1)证明:,,
,
,
,
,
,
;
(2)解:,,
,
,,
,
,
,
,
故答案为:80.
22.
解:(1)在中,,
∴.
由折叠的性质,可知:,,
∴.
又∵∠,
∴
.
故答案为:;
(2).
证明:在中,,
∴.
由折叠的性质,可知:,
∴.
又∵,
∴
,
即.
23.
(1)解:,,
,
,,
,
.
(2)解:平分,
,
,,
,
,
,
,
,
同理可得,
.
24.
(1)解:①∵,,
∴在中,,
∵,
∴,
∵平分,
∴,
∴,
故答案为:;
②∵是是一个外角,
∴,
∵,
∴,
∵,
∴,
∵平分,平分,
∴,,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵是的平分线,
∴,
∴,
∴,
∵平分,
∴,
∴,
