【沪科版七上同步练习】 3.4 二元一次方程组的应用(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 3.4 二元一次方程组的应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 20:37:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】
3.4二元一次方程组的应用
一、单选题
1.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有45张白铁皮,设用张制盒身,张制盒底,恰好配套.则下列方程组中正确的是( )
A. B.
C. D.
2. 某中学八(1)班45名同学参加市“精准扶贫”捐款助学活动,共捐款400元,捐款情况记录表如下:
捐款(元) 3 5 8 10
人数 2 ■ ■ 31
表格中捐款5元和8元的人数不小心被墨水污染看不清楚.若设捐款5元的有x名同学,捐款8元的有y名同学,根据题意可得方程组( )
A. B.
C. D.
3.如图,在一个三角形三个顶点和中心处的每个“ ”中各填有一个式子,如果图中任意三个“ ”中的式子之和均相等,那么a的值为
A.1 B.2 C.3 D.0
二、填空题
4.已知方程 ,用含 的代数式表示 ,则 .
5.若一个长方形的长减少 7cm,宽增加 4cm 成为一个正方形,并且得到的正方形与原长 方形面积相等,则原长方形的长为 -cm.
6.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?根据题意,可求得共有 人.
7.某公司定点到“好客超市”采购A、B两种饮料,8月份采购24件A饮料和32件B饮料共花费了3480元,9月份采购32件A饮料和24件B饮料共花费3240元,10月份该超市A饮料和B饮料中有部分因为保质期临近而打六折促销,公司根据实际需要购买了原价或打折的A饮料和B饮料,共花了2850元,其中打折的A饮料件数是10月份购买所有A饮料和B饮料总件数的,该公司10月份一共购买了A、B饮料 件.
8.《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相同,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各种多少两?设黄金重 两,每枚白银重 两,根据题意可列方程组为 .
9.在学完书中例题后,小聪想用现有的硬纸板裁成如图①的长方形和正方形作为侧面与底面,做成如图②的竖式和横式两种无盖纸盒.已知一张硬纸板的裁剪方式有两种(均有余料)),方式一:裁成3个长方形与一个正方形:方式二:裁成2个长方形与2个正方形.现小聪将m张硬纸板用方式一裁剪,n张硬纸板用方式二裁剪,则:
(1)两种方式共裁出长方形 张,正方形 张(用m、n的代数式表示);
(2)当10<m<15时,所裁得的长方形与正方形纸板恰好用完,做成的两种无盖纸盒一共可能是 个.
三、计算题
10.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.(用方程解)
四、解答题
11. 学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买、两种道具.已知购买1件道具比购买1件道具多10元,购买2件道具和3件道具共需要45元.购买一件道具和一件道具各需要多少元
12.若干名游客要乘坐游船,要求每艘游船乘坐的人数相同.如果每艘游船乘坐12人,结果剩下1人未能上船;若有一艘游船空着开走,则所有游客正好能平均分坐到其余游船上.已知每艘游船最多能容纳15人.请你通过计算,说明游客共有多少人?
五、综合题
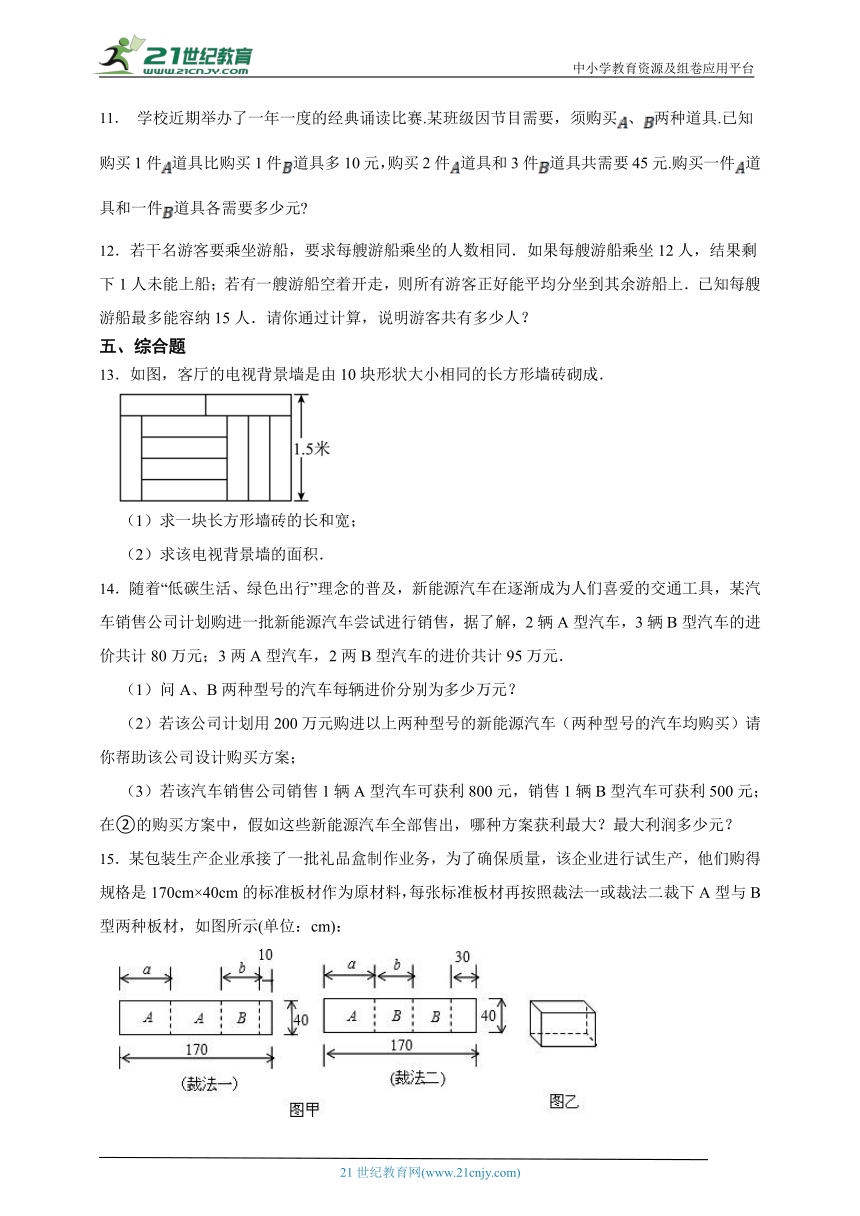
13.如图,客厅的电视背景墙是由10块形状大小相同的长方形墙砖砌成.
(1)求一块长方形墙砖的长和宽;
(2)求该电视背景墙的面积.
14.随着“低碳生活、绿色出行”理念的普及,新能源汽车在逐渐成为人们喜爱的交通工具,某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解,2辆A型汽车,3辆B型汽车的进价共计80万元;3两A型汽车,2两B型汽车的进价共计95万元.
(1)问A、B两种型号的汽车每辆进价分别为多少万元?
(2)若该公司计划用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买)请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利800元,销售1辆B型汽车可获利500元;在②的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润多少元?
15.某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产,他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材,如图所示(单位:cm):
(1)列出方程(组),求出图甲中a与b的值;
(2)在试生产阶段,若将 张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒(每个礼盒用3个A型板材和2个B型板材):
①两种裁法共生产A型板材 张,B型板材 张(用含 的代数式表示);
②当 时,所裁得的A型板材与B型板材恰好用完,做成的横式无盖礼品盒可能是 个(在横线上直接写出所有可能答案,无需书写过程).
六、实践探究题
16.注意:为了使同学们更好地解答本题,我们提供了一种解思路,你可以依照这个思路接下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
某茶叶店经销A,B两种茶,第一次购进了A种茶盒,B种茶盒,共花费元;第二次购进时,两种茶每盒的价格都提高了,该店又购进了A种茶盒,B种茶盒,共花费元,求第一次购进的A,B两种茶每盒的价格.
解题方案:设第一次购进的A种茶每盒的价格为x元,B种茶每盒的价格为y元.
(1)根据题章,列出方程组;
(2)解这个方程组,得.
答:第一次购进的A种茶每盒的价格为 元,B种茶每盒的价格为 元.
答案解析部分
1.【答案】C
【知识点】二元一次方程组的实际应用-配套问题
2.【答案】A
【知识点】二元一次方程组的其他应用;列二元一次方程组
3.【答案】A
【知识点】二元一次方程组的其他应用
4.【答案】
【知识点】二元一次方程的应用
5.【答案】
【知识点】二元一次方程组的应用-几何问题
6.【答案】39
【知识点】二元一次方程组的实际应用-行程问题
7.【答案】60
【知识点】二元一次方程组的应用-和差倍分问题
8.【答案】
【知识点】二元一次方程组的应用-古代数学问题
9.【答案】(1)3m+2n;m+2n
(2)12
【知识点】二元一次方程组的应用-几何问题
10.【答案】解:设甲的速度为x千米/时,乙的速度为y千米/时,
依题意得: ,
解得: .
答:甲的速度为4千米/时,乙的速度为5千米/时.
【知识点】二元一次方程组的实际应用-行程问题
11.【答案】解:设购买一件道具需要元,购买一件道具需要元,
依题意,得:,
解得:
答:购买一件道具需要15元,购买一件道具需要5元.
【知识点】二元一次方程组的其他应用
12.【答案】解:设起初有x艘游船,开走一艘空游船后,平均每艘游船乘坐游客y人.由题意,得:12x+1=y(x-1),即:,∵y是正整数,∴为整数,又∵x为整数,∴x-1=1或13,∴x=2或x=14.当x=2时,y=25>15不合题意,当x=14时,y=13.此时游客人数为13×13=169.答:游客共有169人.
【知识点】二元一次方程的应用
13.【答案】(1)长方形墙砖的长为,宽为
(2)
【知识点】二元一次方程组的应用-几何问题
14.【答案】(1)解:设A型汽车每辆进价为a万元,B型汽车每辆进价为b万元,
由题意得: ,解得: ,
答:A型汽车每辆进价为25万元,B型汽车每辆进价为10万元;
(2)解:设A型汽车购进x辆,B型汽车购进y辆,
由题意得:25x+10y=200,
∵x,y为正整数,
∴ 或 或 ,
答:一共有三种购买方案:购进A型汽车2辆,购进B型汽车15辆;购进A型汽车4辆,购进B型汽车10辆;购进A型汽车6辆,购进B型汽车5辆;
(3)解:由题意可得:利润=800x+500y,
购进A型汽车2辆,购进B型汽车15辆,利润为9100元;
购进A型汽车4辆,购进B型汽车10辆,利润为8200元;
购进A型汽车6辆,购进B型汽车5辆,利润为7300元.
答:购进A型汽车2辆,购进B型汽车15辆,可获得最大利润,利润为9100元.
【知识点】二元一次方程组的实际应用-销售问题
15.【答案】(1)解:由题意得: ,解得 ;
(2)2m+n;m+2n;24或27或30
【知识点】二元一次方程组的应用-几何问题
16.【答案】(1)解:
(2)100;200
【知识点】二元一次方程组的实际应用-销售问题;代入消元法解二元一次方程组;加减消元法解二元一次方程组
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】
3.4二元一次方程组的应用
一、单选题
1.用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现有45张白铁皮,设用张制盒身,张制盒底,恰好配套.则下列方程组中正确的是( )
A. B.
C. D.
2. 某中学八(1)班45名同学参加市“精准扶贫”捐款助学活动,共捐款400元,捐款情况记录表如下:
捐款(元) 3 5 8 10
人数 2 ■ ■ 31
表格中捐款5元和8元的人数不小心被墨水污染看不清楚.若设捐款5元的有x名同学,捐款8元的有y名同学,根据题意可得方程组( )
A. B.
C. D.
3.如图,在一个三角形三个顶点和中心处的每个“ ”中各填有一个式子,如果图中任意三个“ ”中的式子之和均相等,那么a的值为
A.1 B.2 C.3 D.0
二、填空题
4.已知方程 ,用含 的代数式表示 ,则 .
5.若一个长方形的长减少 7cm,宽增加 4cm 成为一个正方形,并且得到的正方形与原长 方形面积相等,则原长方形的长为 -cm.
6.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步.问:人与车各几何?译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少?根据题意,可求得共有 人.
7.某公司定点到“好客超市”采购A、B两种饮料,8月份采购24件A饮料和32件B饮料共花费了3480元,9月份采购32件A饮料和24件B饮料共花费3240元,10月份该超市A饮料和B饮料中有部分因为保质期临近而打六折促销,公司根据实际需要购买了原价或打折的A饮料和B饮料,共花了2850元,其中打折的A饮料件数是10月份购买所有A饮料和B饮料总件数的,该公司10月份一共购买了A、B饮料 件.
8.《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银一枚各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相同,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各种多少两?设黄金重 两,每枚白银重 两,根据题意可列方程组为 .
9.在学完书中例题后,小聪想用现有的硬纸板裁成如图①的长方形和正方形作为侧面与底面,做成如图②的竖式和横式两种无盖纸盒.已知一张硬纸板的裁剪方式有两种(均有余料)),方式一:裁成3个长方形与一个正方形:方式二:裁成2个长方形与2个正方形.现小聪将m张硬纸板用方式一裁剪,n张硬纸板用方式二裁剪,则:
(1)两种方式共裁出长方形 张,正方形 张(用m、n的代数式表示);
(2)当10<m<15时,所裁得的长方形与正方形纸板恰好用完,做成的两种无盖纸盒一共可能是 个.
三、计算题
10.A、B两地相距36千米,甲从A地步行到B地,乙从B地步行到A地,两人同时相向出发,4小时后两人相遇,6小时后,甲剩余的路程是乙剩余路程的2倍,求二人的速度.(用方程解)
四、解答题
11. 学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买、两种道具.已知购买1件道具比购买1件道具多10元,购买2件道具和3件道具共需要45元.购买一件道具和一件道具各需要多少元
12.若干名游客要乘坐游船,要求每艘游船乘坐的人数相同.如果每艘游船乘坐12人,结果剩下1人未能上船;若有一艘游船空着开走,则所有游客正好能平均分坐到其余游船上.已知每艘游船最多能容纳15人.请你通过计算,说明游客共有多少人?
五、综合题
13.如图,客厅的电视背景墙是由10块形状大小相同的长方形墙砖砌成.
(1)求一块长方形墙砖的长和宽;
(2)求该电视背景墙的面积.
14.随着“低碳生活、绿色出行”理念的普及,新能源汽车在逐渐成为人们喜爱的交通工具,某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解,2辆A型汽车,3辆B型汽车的进价共计80万元;3两A型汽车,2两B型汽车的进价共计95万元.
(1)问A、B两种型号的汽车每辆进价分别为多少万元?
(2)若该公司计划用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买)请你帮助该公司设计购买方案;
(3)若该汽车销售公司销售1辆A型汽车可获利800元,销售1辆B型汽车可获利500元;在②的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润多少元?
15.某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产,他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材,如图所示(单位:cm):
(1)列出方程(组),求出图甲中a与b的值;
(2)在试生产阶段,若将 张标准板材用裁法一裁剪,n张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式无盖礼品盒(每个礼盒用3个A型板材和2个B型板材):
①两种裁法共生产A型板材 张,B型板材 张(用含 的代数式表示);
②当 时,所裁得的A型板材与B型板材恰好用完,做成的横式无盖礼品盒可能是 个(在横线上直接写出所有可能答案,无需书写过程).
六、实践探究题
16.注意:为了使同学们更好地解答本题,我们提供了一种解思路,你可以依照这个思路接下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
某茶叶店经销A,B两种茶,第一次购进了A种茶盒,B种茶盒,共花费元;第二次购进时,两种茶每盒的价格都提高了,该店又购进了A种茶盒,B种茶盒,共花费元,求第一次购进的A,B两种茶每盒的价格.
解题方案:设第一次购进的A种茶每盒的价格为x元,B种茶每盒的价格为y元.
(1)根据题章,列出方程组;
(2)解这个方程组,得.
答:第一次购进的A种茶每盒的价格为 元,B种茶每盒的价格为 元.
答案解析部分
1.【答案】C
【知识点】二元一次方程组的实际应用-配套问题
2.【答案】A
【知识点】二元一次方程组的其他应用;列二元一次方程组
3.【答案】A
【知识点】二元一次方程组的其他应用
4.【答案】
【知识点】二元一次方程的应用
5.【答案】
【知识点】二元一次方程组的应用-几何问题
6.【答案】39
【知识点】二元一次方程组的实际应用-行程问题
7.【答案】60
【知识点】二元一次方程组的应用-和差倍分问题
8.【答案】
【知识点】二元一次方程组的应用-古代数学问题
9.【答案】(1)3m+2n;m+2n
(2)12
【知识点】二元一次方程组的应用-几何问题
10.【答案】解:设甲的速度为x千米/时,乙的速度为y千米/时,
依题意得: ,
解得: .
答:甲的速度为4千米/时,乙的速度为5千米/时.
【知识点】二元一次方程组的实际应用-行程问题
11.【答案】解:设购买一件道具需要元,购买一件道具需要元,
依题意,得:,
解得:
答:购买一件道具需要15元,购买一件道具需要5元.
【知识点】二元一次方程组的其他应用
12.【答案】解:设起初有x艘游船,开走一艘空游船后,平均每艘游船乘坐游客y人.由题意,得:12x+1=y(x-1),即:,∵y是正整数,∴为整数,又∵x为整数,∴x-1=1或13,∴x=2或x=14.当x=2时,y=25>15不合题意,当x=14时,y=13.此时游客人数为13×13=169.答:游客共有169人.
【知识点】二元一次方程的应用
13.【答案】(1)长方形墙砖的长为,宽为
(2)
【知识点】二元一次方程组的应用-几何问题
14.【答案】(1)解:设A型汽车每辆进价为a万元,B型汽车每辆进价为b万元,
由题意得: ,解得: ,
答:A型汽车每辆进价为25万元,B型汽车每辆进价为10万元;
(2)解:设A型汽车购进x辆,B型汽车购进y辆,
由题意得:25x+10y=200,
∵x,y为正整数,
∴ 或 或 ,
答:一共有三种购买方案:购进A型汽车2辆,购进B型汽车15辆;购进A型汽车4辆,购进B型汽车10辆;购进A型汽车6辆,购进B型汽车5辆;
(3)解:由题意可得:利润=800x+500y,
购进A型汽车2辆,购进B型汽车15辆,利润为9100元;
购进A型汽车4辆,购进B型汽车10辆,利润为8200元;
购进A型汽车6辆,购进B型汽车5辆,利润为7300元.
答:购进A型汽车2辆,购进B型汽车15辆,可获得最大利润,利润为9100元.
【知识点】二元一次方程组的实际应用-销售问题
15.【答案】(1)解:由题意得: ,解得 ;
(2)2m+n;m+2n;24或27或30
【知识点】二元一次方程组的应用-几何问题
16.【答案】(1)解:
(2)100;200
【知识点】二元一次方程组的实际应用-销售问题;代入消元法解二元一次方程组;加减消元法解二元一次方程组
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
