【沪科版七上同步练习】 第三章 一次方程与方程组(培优)检测题(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 第三章 一次方程与方程组(培优)检测题(含答案) | 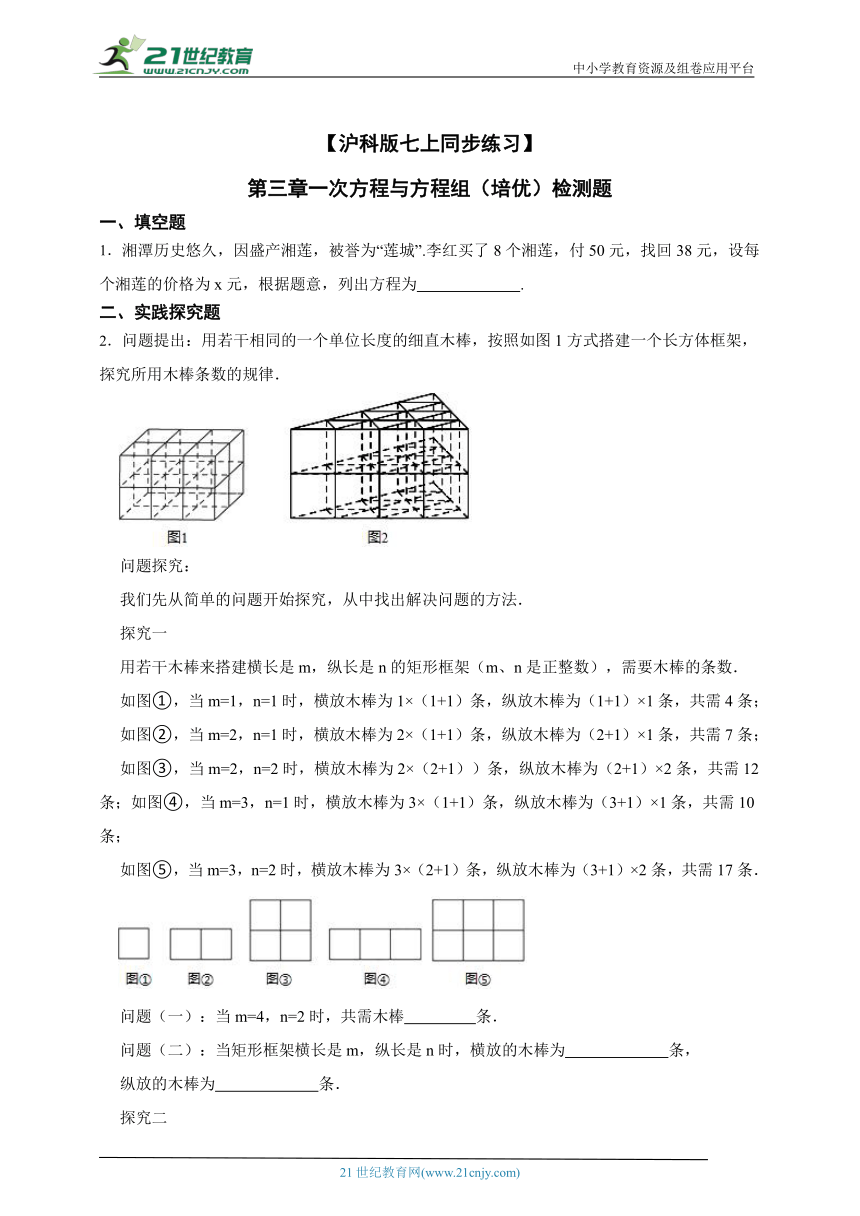 | |
| 格式 | doc | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 20:45:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】
第三章一次方程与方程组(培优)检测题
一、填空题
1.湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个湘莲,付50元,找回38元,设每个湘莲的价格为x元,根据题意,列出方程为 .
二、实践探究题
2.问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
问题(一):当m=4,n=2时,共需木棒 条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
三、计算题
3.解下列一元二次方程
(1)
(2)
4.解方程组:
四、解答题
5.某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润不低于5%,则最多打几折?
6.已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边距离原点8个单位长度,点B在原点的右边.
(1)请直接写出A,B两点所对应的数.
(2)已知,数轴上点M从点A向左出发速度为每秒1个单位长度,同时点N从点B向左出发速度为每秒2个单位长度,经t秒后,求t的值.
五、综合题
7.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
答案解析部分
1.【答案】8x+38=50
【知识点】一元一次方程的实际应用-和差倍分问题
2.【答案】22;m(n+1);n(m+1);[m(n+1)+n(m+1)](s+1);(m+1)(n+1)s;4;1320
【知识点】探索图形规律;一元一次方程的实际应用-几何问题
3.【答案】(1)
(2)
【知识点】解二元一次方程组
4.【答案】解:
把②化为 ,
代入①得 ,
整理得: ,
解得 或 ,
把 代入②得 ,
把 代入②得 ,
∴原方程组的解为 或 .
【知识点】代入消元法解二元一次方程组
5.【答案】解:设可以打x折,
由题意可得, ≥5%
解之可得x≥7
答:最多可以打7折.
【知识点】一元一次方程的实际应用-销售问题
6.【答案】(1)解:点A对应的数为-8,点B对应的数为20.
(2)解:由题意得:当 ,
,
解得,
故经过4秒或28秒后 .
【知识点】数轴上两点之间的距离;数轴的点常规运动模型
7.【答案】(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
【沪科版七上同步练习】
第三章一次方程与方程组(培优)检测题
一、填空题
1.湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个湘莲,付50元,找回38元,设每个湘莲的价格为x元,根据题意,列出方程为 .
二、实践探究题
2.问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
问题(一):当m=4,n=2时,共需木棒 条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
三、计算题
3.解下列一元二次方程
(1)
(2)
4.解方程组:
四、解答题
5.某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润不低于5%,则最多打几折?
6.已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边距离原点8个单位长度,点B在原点的右边.
(1)请直接写出A,B两点所对应的数.
(2)已知,数轴上点M从点A向左出发速度为每秒1个单位长度,同时点N从点B向左出发速度为每秒2个单位长度,经t秒后,求t的值.
五、综合题
7.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
答案解析部分
1.【答案】8x+38=50
【知识点】一元一次方程的实际应用-和差倍分问题
2.【答案】22;m(n+1);n(m+1);[m(n+1)+n(m+1)](s+1);(m+1)(n+1)s;4;1320
【知识点】探索图形规律;一元一次方程的实际应用-几何问题
3.【答案】(1)
(2)
【知识点】解二元一次方程组
4.【答案】解:
把②化为 ,
代入①得 ,
整理得: ,
解得 或 ,
把 代入②得 ,
把 代入②得 ,
∴原方程组的解为 或 .
【知识点】代入消元法解二元一次方程组
5.【答案】解:设可以打x折,
由题意可得, ≥5%
解之可得x≥7
答:最多可以打7折.
【知识点】一元一次方程的实际应用-销售问题
6.【答案】(1)解:点A对应的数为-8,点B对应的数为20.
(2)解:由题意得:当 ,
,
解得,
故经过4秒或28秒后 .
【知识点】数轴上两点之间的距离;数轴的点常规运动模型
7.【答案】(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】
第三章一次方程与方程组(培优)检测题
一、填空题
1.湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个湘莲,付50元,找回38元,设每个湘莲的价格为x元,根据题意,列出方程为 .
二、实践探究题
2.问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
问题(一):当m=4,n=2时,共需木棒 条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
三、计算题
3.解下列一元二次方程
(1)
(2)
4.解方程组:
四、解答题
5.某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润不低于5%,则最多打几折?
6.已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边距离原点8个单位长度,点B在原点的右边.
(1)请直接写出A,B两点所对应的数.
(2)已知,数轴上点M从点A向左出发速度为每秒1个单位长度,同时点N从点B向左出发速度为每秒2个单位长度,经t秒后,求t的值.
五、综合题
7.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
答案解析部分
1.【答案】8x+38=50
【知识点】一元一次方程的实际应用-和差倍分问题
2.【答案】22;m(n+1);n(m+1);[m(n+1)+n(m+1)](s+1);(m+1)(n+1)s;4;1320
【知识点】探索图形规律;一元一次方程的实际应用-几何问题
3.【答案】(1)
(2)
【知识点】解二元一次方程组
4.【答案】解:
把②化为 ,
代入①得 ,
整理得: ,
解得 或 ,
把 代入②得 ,
把 代入②得 ,
∴原方程组的解为 或 .
【知识点】代入消元法解二元一次方程组
5.【答案】解:设可以打x折,
由题意可得, ≥5%
解之可得x≥7
答:最多可以打7折.
【知识点】一元一次方程的实际应用-销售问题
6.【答案】(1)解:点A对应的数为-8,点B对应的数为20.
(2)解:由题意得:当 ,
,
解得,
故经过4秒或28秒后 .
【知识点】数轴上两点之间的距离;数轴的点常规运动模型
7.【答案】(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
【沪科版七上同步练习】
第三章一次方程与方程组(培优)检测题
一、填空题
1.湘潭历史悠久,因盛产湘莲,被誉为“莲城”.李红买了8个湘莲,付50元,找回38元,设每个湘莲的价格为x元,根据题意,列出方程为 .
二、实践探究题
2.问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
问题(一):当m=4,n=2时,共需木棒 条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为 条,
纵放的木棒为 条.
探究二
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为 条,竖放木棒条数为 条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒 条.
三、计算题
3.解下列一元二次方程
(1)
(2)
4.解方程组:
四、解答题
5.某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润不低于5%,则最多打几折?
6.已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边距离原点8个单位长度,点B在原点的右边.
(1)请直接写出A,B两点所对应的数.
(2)已知,数轴上点M从点A向左出发速度为每秒1个单位长度,同时点N从点B向左出发速度为每秒2个单位长度,经t秒后,求t的值.
五、综合题
7.某海鲜排档购进一批大龙虾和海胆,它们的进货单价之和是360元.大龙虾零售单价比进货单价多40元,海胆零售单价比进货单价的1.5倍少60元,按零售单价购买大龙虾2只和海胆4个,共需要1200元.
(1)求大龙虾和海胆的进货单价;
(2)该海鲜排档平均每天卖出大龙虾20只和海胆12个.经调查发现,大龙虾零售单价每降低1元,平均每天就可多售出大龙虾2只,海鲜排档决定把大龙虾的零售单价下降元,海胆的零售单价和销量都不变,在不考虑其他因素的条件下,当a为多少时,海鲜排档每天销售大龙虾和海胆获取的总利润为1490元?
答案解析部分
1.【答案】8x+38=50
【知识点】一元一次方程的实际应用-和差倍分问题
2.【答案】22;m(n+1);n(m+1);[m(n+1)+n(m+1)](s+1);(m+1)(n+1)s;4;1320
【知识点】探索图形规律;一元一次方程的实际应用-几何问题
3.【答案】(1)
(2)
【知识点】解二元一次方程组
4.【答案】解:
把②化为 ,
代入①得 ,
整理得: ,
解得 或 ,
把 代入②得 ,
把 代入②得 ,
∴原方程组的解为 或 .
【知识点】代入消元法解二元一次方程组
5.【答案】解:设可以打x折,
由题意可得, ≥5%
解之可得x≥7
答:最多可以打7折.
【知识点】一元一次方程的实际应用-销售问题
6.【答案】(1)解:点A对应的数为-8,点B对应的数为20.
(2)解:由题意得:当 ,
,
解得,
故经过4秒或28秒后 .
【知识点】数轴上两点之间的距离;数轴的点常规运动模型
7.【答案】(1)大龙虾进货单价为200元,海胆的进货单价为160元
(2)15
【知识点】一元一次方程的其他应用;二元一次方程组的实际应用-销售问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
