【沪科版七上同步练习】 4.4 角的比较和补(余)角(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 4.4 角的比较和补(余)角(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 20:52:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】
4.4角的比较和补(余)角
一、单选题
1.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
2.下列图形中,能用 , , 表示同一个角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.直线AB是平角 B.凡是直角都相等
C.两个锐角之和一定是钝角 D.两条射线组成的图形叫做角
二、填空题
4.已知,则的余角为 .
5.已知∠A=51°23′,则∠A的余角的度数是 .
6.若∠α=40°,那么∠α的补角是 .
7.如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
三、判断题
8.判断下列命题的真假。
(1)一个钝角减去一个锐角,所得的差一定是个锐角;
(2)一个直角减去一个锐角,所得的差一定是个锐角;
(3)若互补两角有一条公共边,则这两个角的平分线所组成的角一定是直角;
(4)相等的两个角一定是对顶角;
(5)如果两个相等的角有一条公共边,那么另一条边一定在同一条直线上.
四、计算题
9.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
10.计算:
(1)40°26'+30°30'30″÷6
(2)13°53'×3-32°5'31″
五、解答题
11.如图,∠AOB=90°,OE平分∠AOB,OD平分∠BOC,∠EOD=70°,求∠BOC的度数.
12.一个角的余角比它的补角的 还少 ,求这个角的度数.
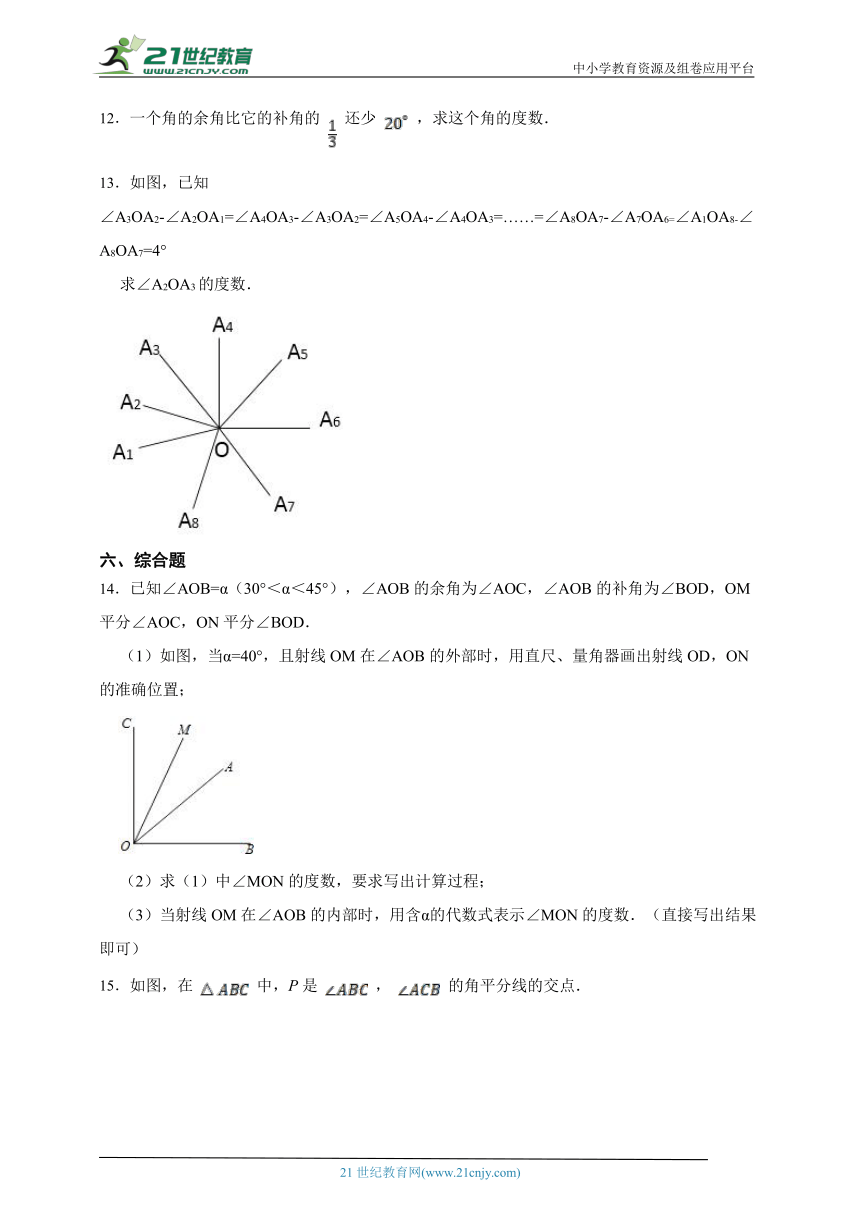
13.如图,已知∠A3OA2-∠A2OA1=∠A4OA3-∠A3OA2=∠A5OA4-∠A4OA3=……=∠A8OA7-∠A7OA6=∠A1OA8-∠A8OA7=4°
求∠A2OA3的度数.
六、综合题
14.已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
15.如图,在 中,P是 , 的角平分线的交点.
(1)若 ,求 的度数;
(2)有位同学在解答(1)后得出 的规律,你认为正确吗?请说明理由.
16.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
七、实践探究题
17.如图1,中,,点D在上,且,求证:.小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作平分,与相交于点E.
方法2:如图3,作,与相交于点F.
(1)根据阅读材料,分别运用以上两种方法,证明.
(2)用学过的知识或参考小明的方法,解决下面的问题:
如图4,中,点D在上,点E在上,且,点F在上,且,延长,相交于点G,且.在图中找出与相等的角,并加以证明.
答案解析部分
1.【答案】B
【知识点】角的运算
2.【答案】B
【知识点】角的概念及表示
3.【答案】B
【知识点】角的概念及表示;角的运算
4.【答案】30°
【知识点】余角、补角及其性质
5.【答案】38°37′
【知识点】角的运算
6.【答案】140
【知识点】余角、补角及其性质
7.【答案】①③④
【知识点】直线、射线、线段;角的运算
8.【答案】(1)错误
(2)正确
(3)错误
(4)错误
(5)错误
【知识点】角的概念及表示;余角、补角及其性质;角的大小比较
9.【答案】解:∵∠AOB=90°,OC平分∠AOB∴∠BOC= ∠AOB=45°∵∠BOD=∠COD﹣∠BOC=90°﹣45°=45°∠BOD=3∠DOE∴∠DOE=15°∴∠COE=∠COD﹣∠DOE=90°﹣15°=75°
【知识点】角的运算;余角、补角及其性质;角平分线的概念
10.【答案】(1)解:40°26'+30°30'30″÷6
=40°26'+5°5'5″
=45°31'5″
(2)解:13°53'×3-32°5'31″
=41°39'-32°5'31″
=9°33'29″
【知识点】角的运算
11.【答案】解:∵OE平分∠AOB,∠AOB=90°,
∴∠EOB=∠AOB=×90°=45°
又 ∵∠EOD=70°,∠EOB=45°
∴∠BOD=70°-45°=25°
又 ∵OD平分∠BOC,∠BOD=25°
∴∠BOC=2×25°=50°
【知识点】角的运算;角平分线的概念
12.【答案】解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),根据题意可,得90°﹣x= (180°﹣x)﹣20°,解得x=75°.故答案为75°.
【知识点】余角、补角及其性质
13.【答案】解:设∠A2OA1=x°,
∵∠A3OA2-∠A2OA1=4°,
∠A4OA3-∠A3OA2=4°,
∠A5OA4-∠A4OA3=4°,
∠A6OA5-∠A5OA4=4°,
∠A7OA6-∠A6OA5=4°,
∠A8OA7-∠A7OA6=4°,
∠A1OA8-∠A8OA7=4°,
∴∠A3OA2=4°+x°,
∠A4OA3=4°+4°+x°=4°×2+x°,
∠A5OA4=4°+4°×2+x°=4°×3+x°,
∠A6OA5=4°+4°×3+x°=4°×4+x°,
∠A7OA6=4°+4°×4+x°=4°×5+x°,
∠A8OA7=4°+4°×5+x°=4°×6+x°,
∠A1OA8=4°+4°×6+x°=4°×7+x°,
又∵∠A1OA2+∠A2OA3+∠A3OA4+∠A4OA5+∠A5OA6+∠A6OA7+∠A7OA8+∠A8OA1=360°,
∴x°+4°+x°+4°×2+x°+4°×3+x°+4°×4+x°+4°×5+x°+4°×6+x°+4°×7+x°=360°,
8x°+4°×(1+2+3+4+5+6+7)=360°,
8x°+4°×=360°,
x°+14°=45°,
∴x°=31°.
∴∠A3OA2=4°+x°=4°+31°=35°
【知识点】角的运算
14.【答案】(1)解 :如图1,图2所示;
(2)解 :∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,∴∠AOC=90°﹣∠AOB=50°,∠BOD=180°﹣∠AOB=140°,∵OM平分∠AOC,ON平分∠BOD,∴∠MOA= ∠AOC= ×50°=25°,∠BON= ∠BOD= ×140°=70°,①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°,
②如图2,∠MON=∠NOB﹣∠MOA﹣∠AOB=70°﹣25°﹣40°=5°,
∴∠MON=135°或5°
(3)解 :∠MON=α+45°或135°﹣2α
【知识点】余角、补角及其性质;角的大小比较;角平分线的概念
15.【答案】(1)解: ,得到∠ABC+∠ACB=100° ,
BP,CP分别平分 , ,
,
.
(2)解:我认为正确.理由如下:
BP,CP分别平分 , ,
,
,
.
【知识点】角的运算;角平分线的概念
16.【答案】(1)解:∵三角板绕点O按每秒10°的速度沿逆时针方向旋转,
∴第t秒时,三角板转过的角度为10°t,
当三角板转到如图①所示时,∠AON=∠CON
∵∠AON=90°+10°t,∠CON=∠BOC+∠BON=120°+90°﹣10°t=210°﹣10°t
∴90°+10°t=210°﹣10°t
即t=6;
当三角板转到如图②所示时,∠AOC=∠CON=180°﹣120°=60°
∵∠CON=∠BOC﹣∠BON=120°﹣(10°t﹣90°)=210°﹣10°t
∴210°﹣10°t=60°
即t=15;
当三角板转到如图③所示时,∠AON=∠CON= ,
∵∠CON=∠BON﹣∠BOC=(10°t﹣90°)﹣120°=10°t﹣210°
∴10°t﹣210°=30°
即t=24;
当三角板转到如图④所示时,∠AON=∠AOC=60°
∵∠AON=10°t﹣180°﹣90°=10°t﹣270°
∴10°t﹣270°=60°
即t=33.
故t的值为6、15、24、33.
(2)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°
【知识点】角的运算
17.【答案】(1)证明:方法1:作平分,与相交于点E,
∴,
∵,
∴,
∵,,
∴,
∴,
∴;
方法2:∵,,
∴,
∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴;
(2)解:,证明如下:
∵,
,
∴;
【知识点】角的运算;角平分线的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】
4.4角的比较和补(余)角
一、单选题
1.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
2.下列图形中,能用 , , 表示同一个角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.直线AB是平角 B.凡是直角都相等
C.两个锐角之和一定是钝角 D.两条射线组成的图形叫做角
二、填空题
4.已知,则的余角为 .
5.已知∠A=51°23′,则∠A的余角的度数是 .
6.若∠α=40°,那么∠α的补角是 .
7.如图,点C,D在线段BE上(C在D的左侧),点A在线段BE外,连接AB,AC,AD,AE,已知∠BAE = 120°,∠CAD = 60°,有下列说法:①直线CD上以B,C,D,E为端点的线段共有6条;②作∠BAM= ∠BAD,∠EAN= ∠EAC.则∠MAN=30°;③以A为顶点的所有小于平角的角的度数和为420°;④若BC=2,CD=DE=3,点F是线段BE上任意一点,则点F到点B,C,D,E的距离之和最大值为17,最小值为11.其中说法正确的有 .(填上所有正确说法的序号)
三、判断题
8.判断下列命题的真假。
(1)一个钝角减去一个锐角,所得的差一定是个锐角;
(2)一个直角减去一个锐角,所得的差一定是个锐角;
(3)若互补两角有一条公共边,则这两个角的平分线所组成的角一定是直角;
(4)相等的两个角一定是对顶角;
(5)如果两个相等的角有一条公共边,那么另一条边一定在同一条直线上.
四、计算题
9.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.
10.计算:
(1)40°26'+30°30'30″÷6
(2)13°53'×3-32°5'31″
五、解答题
11.如图,∠AOB=90°,OE平分∠AOB,OD平分∠BOC,∠EOD=70°,求∠BOC的度数.
12.一个角的余角比它的补角的 还少 ,求这个角的度数.
13.如图,已知∠A3OA2-∠A2OA1=∠A4OA3-∠A3OA2=∠A5OA4-∠A4OA3=……=∠A8OA7-∠A7OA6=∠A1OA8-∠A8OA7=4°
求∠A2OA3的度数.
六、综合题
14.已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
15.如图,在 中,P是 , 的角平分线的交点.
(1)若 ,求 的度数;
(2)有位同学在解答(1)后得出 的规律,你认为正确吗?请说明理由.
16.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
七、实践探究题
17.如图1,中,,点D在上,且,求证:.小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作平分,与相交于点E.
方法2:如图3,作,与相交于点F.
(1)根据阅读材料,分别运用以上两种方法,证明.
(2)用学过的知识或参考小明的方法,解决下面的问题:
如图4,中,点D在上,点E在上,且,点F在上,且,延长,相交于点G,且.在图中找出与相等的角,并加以证明.
答案解析部分
1.【答案】B
【知识点】角的运算
2.【答案】B
【知识点】角的概念及表示
3.【答案】B
【知识点】角的概念及表示;角的运算
4.【答案】30°
【知识点】余角、补角及其性质
5.【答案】38°37′
【知识点】角的运算
6.【答案】140
【知识点】余角、补角及其性质
7.【答案】①③④
【知识点】直线、射线、线段;角的运算
8.【答案】(1)错误
(2)正确
(3)错误
(4)错误
(5)错误
【知识点】角的概念及表示;余角、补角及其性质;角的大小比较
9.【答案】解:∵∠AOB=90°,OC平分∠AOB∴∠BOC= ∠AOB=45°∵∠BOD=∠COD﹣∠BOC=90°﹣45°=45°∠BOD=3∠DOE∴∠DOE=15°∴∠COE=∠COD﹣∠DOE=90°﹣15°=75°
【知识点】角的运算;余角、补角及其性质;角平分线的概念
10.【答案】(1)解:40°26'+30°30'30″÷6
=40°26'+5°5'5″
=45°31'5″
(2)解:13°53'×3-32°5'31″
=41°39'-32°5'31″
=9°33'29″
【知识点】角的运算
11.【答案】解:∵OE平分∠AOB,∠AOB=90°,
∴∠EOB=∠AOB=×90°=45°
又 ∵∠EOD=70°,∠EOB=45°
∴∠BOD=70°-45°=25°
又 ∵OD平分∠BOC,∠BOD=25°
∴∠BOC=2×25°=50°
【知识点】角的运算;角平分线的概念
12.【答案】解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),根据题意可,得90°﹣x= (180°﹣x)﹣20°,解得x=75°.故答案为75°.
【知识点】余角、补角及其性质
13.【答案】解:设∠A2OA1=x°,
∵∠A3OA2-∠A2OA1=4°,
∠A4OA3-∠A3OA2=4°,
∠A5OA4-∠A4OA3=4°,
∠A6OA5-∠A5OA4=4°,
∠A7OA6-∠A6OA5=4°,
∠A8OA7-∠A7OA6=4°,
∠A1OA8-∠A8OA7=4°,
∴∠A3OA2=4°+x°,
∠A4OA3=4°+4°+x°=4°×2+x°,
∠A5OA4=4°+4°×2+x°=4°×3+x°,
∠A6OA5=4°+4°×3+x°=4°×4+x°,
∠A7OA6=4°+4°×4+x°=4°×5+x°,
∠A8OA7=4°+4°×5+x°=4°×6+x°,
∠A1OA8=4°+4°×6+x°=4°×7+x°,
又∵∠A1OA2+∠A2OA3+∠A3OA4+∠A4OA5+∠A5OA6+∠A6OA7+∠A7OA8+∠A8OA1=360°,
∴x°+4°+x°+4°×2+x°+4°×3+x°+4°×4+x°+4°×5+x°+4°×6+x°+4°×7+x°=360°,
8x°+4°×(1+2+3+4+5+6+7)=360°,
8x°+4°×=360°,
x°+14°=45°,
∴x°=31°.
∴∠A3OA2=4°+x°=4°+31°=35°
【知识点】角的运算
14.【答案】(1)解 :如图1,图2所示;
(2)解 :∵∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,∴∠AOC=90°﹣∠AOB=50°,∠BOD=180°﹣∠AOB=140°,∵OM平分∠AOC,ON平分∠BOD,∴∠MOA= ∠AOC= ×50°=25°,∠BON= ∠BOD= ×140°=70°,①如图1,∠MON=∠MOA+∠AOB+∠BON=25°+40°+70°=135°,
②如图2,∠MON=∠NOB﹣∠MOA﹣∠AOB=70°﹣25°﹣40°=5°,
∴∠MON=135°或5°
(3)解 :∠MON=α+45°或135°﹣2α
【知识点】余角、补角及其性质;角的大小比较;角平分线的概念
15.【答案】(1)解: ,得到∠ABC+∠ACB=100° ,
BP,CP分别平分 , ,
,
.
(2)解:我认为正确.理由如下:
BP,CP分别平分 , ,
,
,
.
【知识点】角的运算;角平分线的概念
16.【答案】(1)解:∵三角板绕点O按每秒10°的速度沿逆时针方向旋转,
∴第t秒时,三角板转过的角度为10°t,
当三角板转到如图①所示时,∠AON=∠CON
∵∠AON=90°+10°t,∠CON=∠BOC+∠BON=120°+90°﹣10°t=210°﹣10°t
∴90°+10°t=210°﹣10°t
即t=6;
当三角板转到如图②所示时,∠AOC=∠CON=180°﹣120°=60°
∵∠CON=∠BOC﹣∠BON=120°﹣(10°t﹣90°)=210°﹣10°t
∴210°﹣10°t=60°
即t=15;
当三角板转到如图③所示时,∠AON=∠CON= ,
∵∠CON=∠BON﹣∠BOC=(10°t﹣90°)﹣120°=10°t﹣210°
∴10°t﹣210°=30°
即t=24;
当三角板转到如图④所示时,∠AON=∠AOC=60°
∵∠AON=10°t﹣180°﹣90°=10°t﹣270°
∴10°t﹣270°=60°
即t=33.
故t的值为6、15、24、33.
(2)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°
【知识点】角的运算
17.【答案】(1)证明:方法1:作平分,与相交于点E,
∴,
∵,
∴,
∵,,
∴,
∴,
∴;
方法2:∵,,
∴,
∵,
∴,
∴,
∴,
∴,
又∵,
∴,
∴;
(2)解:,证明如下:
∵,
,
∴;
【知识点】角的运算;角平分线的概念
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
