3.2图形的旋转同步练习(含简单答案)北师大版数学八年级下册
文档属性
| 名称 | 3.2图形的旋转同步练习(含简单答案)北师大版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 689.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 17:30:51 | ||
图片预览

文档简介
3.2 图形的旋转
一、单选题
1.如图,在平面直角坐标系中,将绕着旋转中心顺时针旋转,得到,则旋转中心的坐标为( )
A. B.
C. D.
2.如图,将绕直角顶点C逆时针旋转,使得点B落在斜边上的处得.若,则的度数为( )
A. B. C. D.
3.如图,将绕点顺时针旋转得,点的对应点恰好落在延长线上,连接.下列结论一定正确的是( )
A. B. C. D.
4.如图,在ABC中,∠CAB=65°,在同一平面内,将ABC绕点A旋转到的位置,使得,则的度数为( )
A.70° B.50° C.40° D.35°
5.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在平面内,可作为旋转中心的点个数( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,将绕某个点旋转一定的角度后得到,上的一点随旋转后的对应点的坐标是( )
A. B. C. D.
7.如图,在中,,将绕点B顺时针旋转得到,点A,C的对应点分别为D,E.当的延长线经过点C时,则下列结论一定正确的是( )
A. B. C. D.
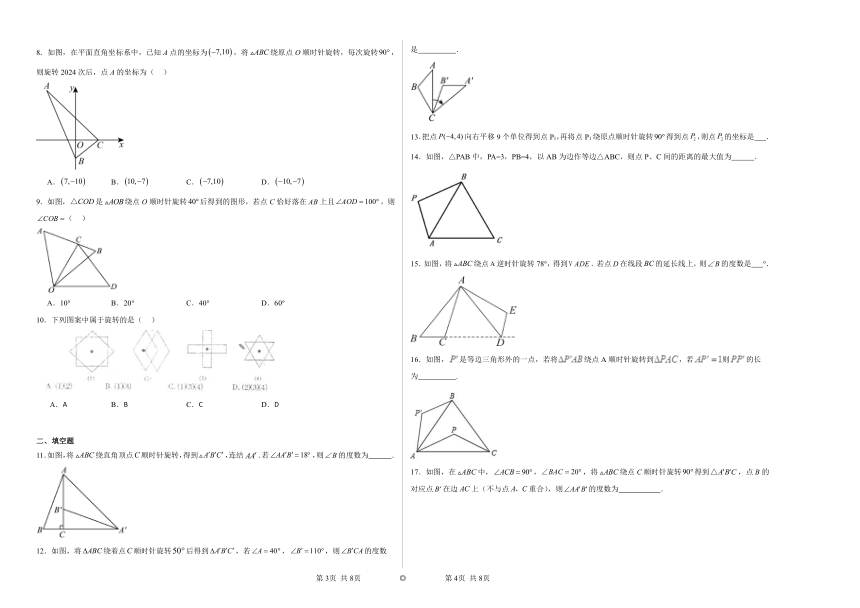
8.如图,在平面直角坐标系中,已知A点的坐标为,将绕原点O顺时针旋转,每次旋转,则旋转2024次后,点A的坐标为( )
A. B. C. D.
9.如图,是绕点O顺时针旋转后得到的图形,若点C恰好落在上且,则( )
A.10° B.20° C.40° D.60°
10.下列图案中属于旋转的是( )
A.A B.B C.C D.D
二、填空题
11.如图,将绕直角顶点顺时针旋转,得到,连结.若,则的度数为 .
12.如图,将绕着点顺时针旋转后得到,若,,则的度数是 .
13.把点向右平移9个单位得到点P1,再将点P1绕原点顺时针旋转得到点,则点的坐标是 .
14.如图,△PAB中,PA=3,PB=4,以AB为边作等边△ABC,则点P、C间的距离的最大值为 .
15.如图,将绕点逆时针旋转78°,得到.若点在线段的延长线上,则的度数是 °.
16.如图,是等边三角形外的一点,若将绕点A顺时针旋转到,若则的长为 .
17.如图,在中,,,将绕点C顺时针旋转得到,点B的对应点在边上(不与点重合),则的度数为 .
18.如图,在中,,将绕点顺时针旋转后得到(点的对应点是,点的对应点是),连接.若,则 .
19.如图:已知,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程 .
20.如图,在平面直角坐标系中,点的坐标为,点在轴上,,将绕点顺时针旋转得到,则点的坐标为 .
三、解答题
21.已知,在四边形中,,连接.
(1)如图1,若,,,求的面积;
(2)如图2,若,平分,求证:;
(3)如图3,在(2)的条件下,若点P是射线上一动点,连接.将线段绕着点D顺时针旋转,点P的对应点为,若,请直接写出的最小值.
22.如图,已知和直线.
(1)分别写出点关于直线的对称点和关于原点的对称点的坐标;
(2)若点是点关于原点的对称点,判断四边形的形状,并说明理由.
23.实践与探究
【问题提出】已知三条射线、、,若其中一条射线平分另两条射线所组成的角时(如下图中),我们称、、组成的图形为“角分图形”.
【问题探究】在一次数学活动课上,小明和小亮同学用一个含角的直角三角板做分角实验.如图1,在直线上取一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
小明同学将图1中的三角板绕点逆时针旋转,使一边在的内部,如图2.小明发现此时、、组成的图形为“角分图形”,请说明理由.
【类比探究】
小亮同学将图1中的三角板绕点以每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,发现射线、、恰好构成“角分图形”,请求出的值.
【问题拓展】
小明同学将图1中的三角板绕点顺时针旋转至图3,使在的内部,问题:在旋转过程中,与的差是否发生变化 若不变,请求出这个差值;若变化,请求出差的变化范围.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.D
3.C
4.B
5.C
6.C
7.C
8.C
9.B
10.C
11.
12.
13.
14.7
15.51
16.1.
17./25度
18.13
19.答案不唯一(例:先将△ABC以点B为旋转中心顺时针旋转90,再将得到的图形向右平移2个单位向下平移2个单位即可).
20.
21.(1) (2)略 (3)的最小值是
22.(1), (2)矩形,略
23.问题探究:略
类比探究:秒或秒或秒
问题拓展:不变,
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在平面直角坐标系中,将绕着旋转中心顺时针旋转,得到,则旋转中心的坐标为( )
A. B.
C. D.
2.如图,将绕直角顶点C逆时针旋转,使得点B落在斜边上的处得.若,则的度数为( )
A. B. C. D.
3.如图,将绕点顺时针旋转得,点的对应点恰好落在延长线上,连接.下列结论一定正确的是( )
A. B. C. D.
4.如图,在ABC中,∠CAB=65°,在同一平面内,将ABC绕点A旋转到的位置,使得,则的度数为( )
A.70° B.50° C.40° D.35°
5.如图,如果正方形ABCD旋转后能与正方形CDEF重合,那么图形所在平面内,可作为旋转中心的点个数( )
A.1个 B.2个 C.3个 D.4个
6.如图,在平面直角坐标系中,将绕某个点旋转一定的角度后得到,上的一点随旋转后的对应点的坐标是( )
A. B. C. D.
7.如图,在中,,将绕点B顺时针旋转得到,点A,C的对应点分别为D,E.当的延长线经过点C时,则下列结论一定正确的是( )
A. B. C. D.
8.如图,在平面直角坐标系中,已知A点的坐标为,将绕原点O顺时针旋转,每次旋转,则旋转2024次后,点A的坐标为( )
A. B. C. D.
9.如图,是绕点O顺时针旋转后得到的图形,若点C恰好落在上且,则( )
A.10° B.20° C.40° D.60°
10.下列图案中属于旋转的是( )
A.A B.B C.C D.D
二、填空题
11.如图,将绕直角顶点顺时针旋转,得到,连结.若,则的度数为 .
12.如图,将绕着点顺时针旋转后得到,若,,则的度数是 .
13.把点向右平移9个单位得到点P1,再将点P1绕原点顺时针旋转得到点,则点的坐标是 .
14.如图,△PAB中,PA=3,PB=4,以AB为边作等边△ABC,则点P、C间的距离的最大值为 .
15.如图,将绕点逆时针旋转78°,得到.若点在线段的延长线上,则的度数是 °.
16.如图,是等边三角形外的一点,若将绕点A顺时针旋转到,若则的长为 .
17.如图,在中,,,将绕点C顺时针旋转得到,点B的对应点在边上(不与点重合),则的度数为 .
18.如图,在中,,将绕点顺时针旋转后得到(点的对应点是,点的对应点是),连接.若,则 .
19.如图:已知,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程 .
20.如图,在平面直角坐标系中,点的坐标为,点在轴上,,将绕点顺时针旋转得到,则点的坐标为 .
三、解答题
21.已知,在四边形中,,连接.
(1)如图1,若,,,求的面积;
(2)如图2,若,平分,求证:;
(3)如图3,在(2)的条件下,若点P是射线上一动点,连接.将线段绕着点D顺时针旋转,点P的对应点为,若,请直接写出的最小值.
22.如图,已知和直线.
(1)分别写出点关于直线的对称点和关于原点的对称点的坐标;
(2)若点是点关于原点的对称点,判断四边形的形状,并说明理由.
23.实践与探究
【问题提出】已知三条射线、、,若其中一条射线平分另两条射线所组成的角时(如下图中),我们称、、组成的图形为“角分图形”.
【问题探究】在一次数学活动课上,小明和小亮同学用一个含角的直角三角板做分角实验.如图1,在直线上取一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
小明同学将图1中的三角板绕点逆时针旋转,使一边在的内部,如图2.小明发现此时、、组成的图形为“角分图形”,请说明理由.
【类比探究】
小亮同学将图1中的三角板绕点以每秒的速度沿逆时针方向旋转一周,在旋转的过程中,第秒时,发现射线、、恰好构成“角分图形”,请求出的值.
【问题拓展】
小明同学将图1中的三角板绕点顺时针旋转至图3,使在的内部,问题:在旋转过程中,与的差是否发生变化 若不变,请求出这个差值;若变化,请求出差的变化范围.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.D
3.C
4.B
5.C
6.C
7.C
8.C
9.B
10.C
11.
12.
13.
14.7
15.51
16.1.
17./25度
18.13
19.答案不唯一(例:先将△ABC以点B为旋转中心顺时针旋转90,再将得到的图形向右平移2个单位向下平移2个单位即可).
20.
21.(1) (2)略 (3)的最小值是
22.(1), (2)矩形,略
23.问题探究:略
类比探究:秒或秒或秒
问题拓展:不变,
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
