人教版八年级数学上册 11.3 多边形及其内角和 同步练习 (含解析)
文档属性
| 名称 | 人教版八年级数学上册 11.3 多边形及其内角和 同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 602.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-15 21:26:01 | ||
图片预览


文档简介
11.3 多边形及其内角和
一、单选题
1.下列多边形中,内角和等于的是( )
A. B. C. D.
2.十二边形的外角和为( )
A. B. C. D.
3.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
4.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
5.六边形的内角和是( )
A.180° B.360° C.540° D.720°
6.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
7.下列命题是真命题的是( )
A.五边形的内角和是 B.三角形的任意两边之和大于第三边
C.内错角相等 D.三角形的重心是这个三角形的三条角平分线的交点
8.如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角( )
A. B. C. D.
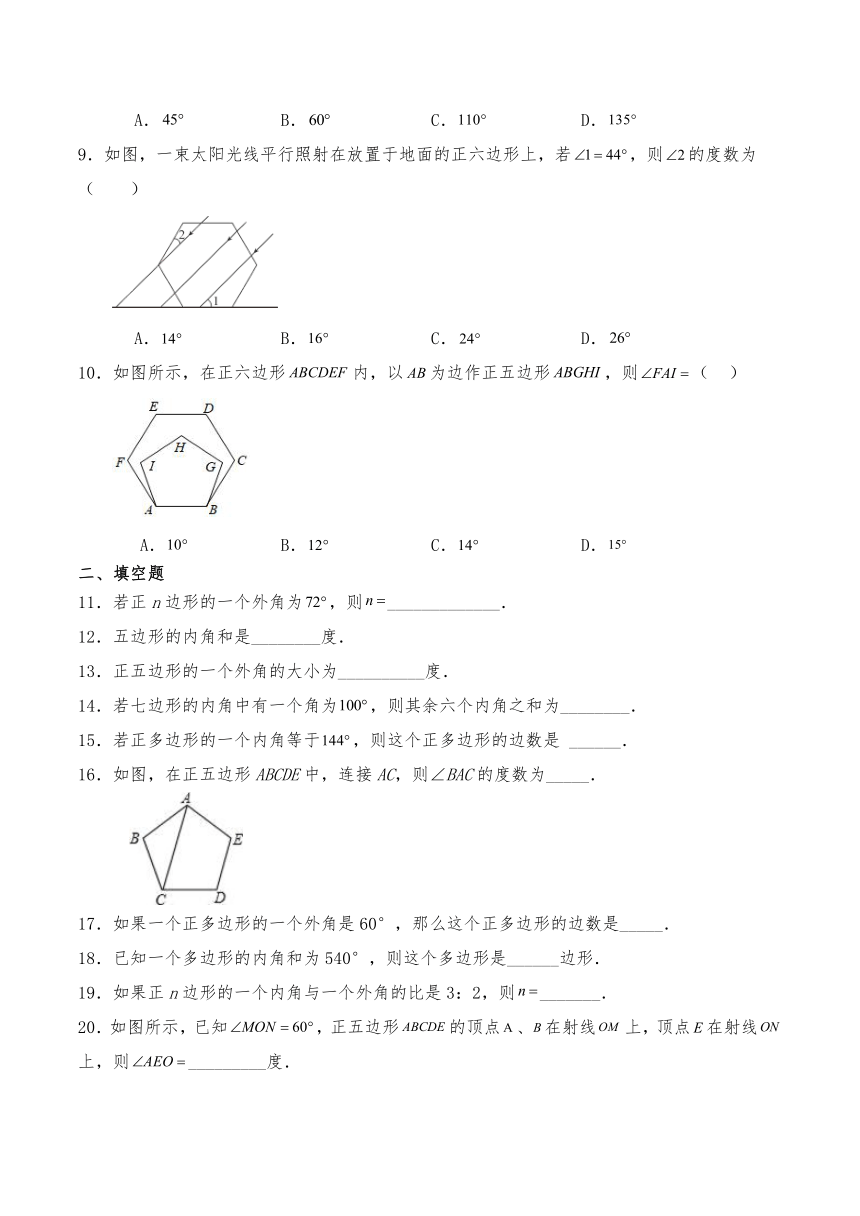
9.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
10.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
二、填空题
11.若正n边形的一个外角为,则_____________.
12.五边形的内角和是________度.
13.正五边形的一个外角的大小为__________度.
14.若七边形的内角中有一个角为,则其余六个内角之和为________.
15.若正多边形的一个内角等于,则这个正多边形的边数是 ______.
16.如图,在正五边形ABCDE中,连接AC,则∠BAC的度数为_____.
17.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是_____.
18.已知一个多边形的内角和为540°,则这个多边形是______边形.
19.如果正n边形的一个内角与一个外角的比是3:2,则_______.
20.如图所示,已知,正五边形的顶点、在射线上,顶点在射线上,则_________度.
三、解答题
21.一个多边形,它的内角和比外角和的4倍多,求这个多边形的边数及内角和度数.
22.如图,,,的平分线与的平分线交于点,求的度数.
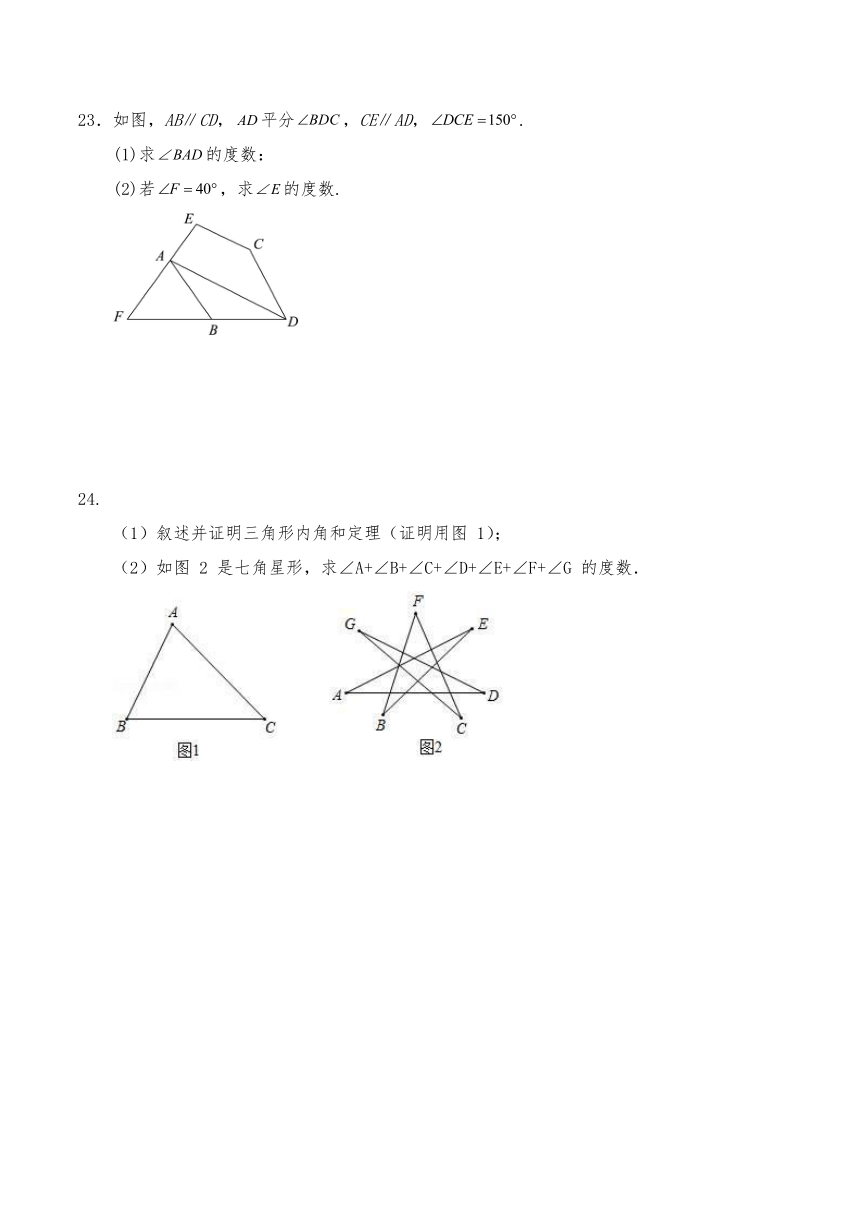
23.如图,AB∥CD,平分,CE∥AD,.
(1)求的度数:
(2)若,求的度数.
24.
(1)叙述并证明三角形内角和定理(证明用图 1);
(2)如图 2 是七角星形,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.
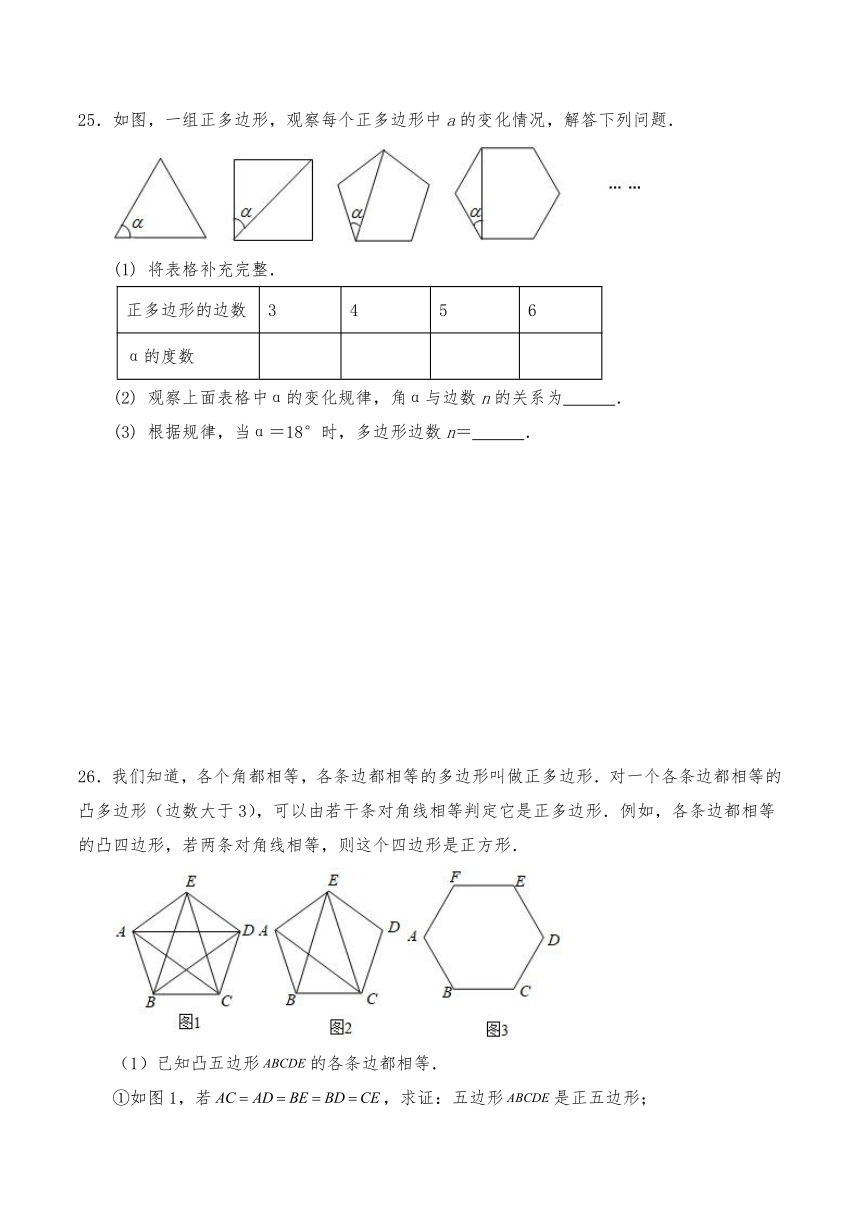
25.如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题.
将表格补充完整.
正多边形的边数 3 4 5 6
α的度数
观察上面表格中α的变化规律,角α与边数n的关系为 .
根据规律,当α=18°时,多边形边数n= .
26.我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形的各条边都相等.
①如图1,若,求证:五边形是正五边形;
②如图2,若,请判断五边形是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形的各条边都相等.
①若,则六边形是正六边形;( )
②若,则六边形是正六边形. ( )
答案
一、单选题
1.B
【分析】根据n边形内角和公式分别求解后,即可得到答案
解:A.三角形内角和是,故选项不符合题意;
B.四边形内角和为,故选项符合题意;
C.五边形内角和为,故选项不符合题意;
D.六边形内角和为,故选项不符合题意.
故选:B.
2.C
【分析】根据多边形的外角和为360°进行解答即可.
解:∵多边形的外角和为360°
∴十二边形的外角和是360°.
故选:C.
3.C
【分析】设这个外角是x°,则内角是3x°,根据内角与它相邻的外角互补列出方程求出外角的度数,根据多边形的外角和是360°即可求解.
解:∵一个正多边形每个内角与它相邻外角的度数比为3:1,
∴设这个外角是x°,则内角是3x°,
根据题意得:x+3x=180°,
解得:x=45°,
360°÷45°=8(边),
故选:C.
4.A
【分析】根据n边形的内角和是(n﹣2) 180°,列出方程即可求解.
解:根据n边形的内角和公式,得
(n﹣2) 180°=900°,
解得n=7,
∴这个多边形的边数是7,
故选:A.
5.D
【分析】根据多边形的内角和公式解答即可.
解:六边形的内角和是:;
故选:D.
6.C
【分析】进行平面镶嵌就是在同一顶点处的几个多边形的内角和应是,因此我们只需要验证是不是上面所给的几个正多边形的一个内角度数的整数倍即可.
解:A、等边三角形每个内角的度数为,,故该项不符合题意;
B、正方形的每个内角的度数为,,故该项不符合题意;
C、正五边形的每个内角的度数为,,故该项符合题意;
D、正六边形的每个内角的度数为,,故该项不符合题意;
故选:C.
7.B
【分析】根据相关概念逐项分析即可.
解:A、五边形的内角和是,故原命题为假命题,不符合题意;
B、三角形的任意两边之和大于第三边,原命题是真命题,符合题意;
C、两直线平行,内错角相等,故原命题为假命题,不符合题意;
D、三角形的重心是这个三角形的三条中线的交点,故原命题为假命题,不符合题意;
故选:B.
8.A
【分析】由正八边形的外角和为,结合正八边形的每一个外角都相等,再列式计算即可.
解:∵正八边形的外角和为,
∴,
故选A
9.B
【分析】如图,求出正六边形的一个内角和一个外角的度数,得到,平行线的性质,得到,三角形的外角的性质,得到,进而求出的度数.
解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;
故选B.
10.B
【分析】利用正n边形的外角和定理计算即可
解:如图,延长BA到点O,
∵六边形ABCDEF是正六边形,
∴∠FAO==60°,
∵五边形ABGHI是正五边形,
∴∠IAO==72°,
∴∠FAI=∠IAO-∠FAO=12°,
故选B.
二、填空题
11.5
【分析】正多边形的外角和为,每一个外角都相等,由此计算即可.
解:由题意知,,
故答案为:5.
12.540
【分析】根据n边形内角和为求解即可.
解:五边形的内角和是.
故答案为:540.
13.72
【分析】根据多边形的外角和是360°,依此即可求解.
解:正五边形的一个外角的度数为:,
故答案为:72.
14.
【分析】根据多边形的内角和公式即可得.
解:∵七边形的内角中有一个角为,
∴其余六个内角之和为,
故答案为:.
15.10
【分析】本题需先根据已知条件设出正多边形的边数,再根据正多边形的计算公式得出结果即可.
解:设这个正多边形是正n边形,根据题意得:
,
解得:.
故答案为:10.
16.36°
【分析】首先利用多边形的内角和公式求得正五边形的内角和,再求得每个内角的度数,利用等腰三角形的性质可得∠BAC的度数.
解:正五边形内角和:(5﹣2)×180°=3×180°=540°
∴,
∴ .
故答案为36°.
17.6
解:根据多边形的外角和等于360°和正多边形的每一个外角都相等,得多边形的边数为360°÷60°=6.
故答案为:6.
18.5
解:设这个多边形是n边形,由题意得,
(n-2) ×180°=540°,解之得,n=5.
19.5
【分析】设多边形的一个内角为3x度,一个外角则为2x度,求得外角的度数,然后根据多边形的外角和为360°,进而求出n的值.
解:∵正边形的一个内角度数与其外角度数的比是3:2,
∴设多边形的一个内角为3x度,一个外角则为2x度,
∴3x+2x=180°,
解得x=36°,
∴一个外角为2x=72°,
360°÷72°=5,
∴n=5,
故答案为:5.
20.48
【分析】是正五边形的一个外角,利用多边形外交和360°算出一个外角,再利用的内角和180°,即可算出
解:∵四边形ABCDE是正五边形,是一个外角
∴
在中:
故答案为:48
三、解答题
21.
解:根据题意,得
(n 2) 180°=360°×4+180°,
解得:n=11.
360°×4+180°=1620°
则这个多边形的边数是11,内角和度数是1620度.
22.
解:过点作,如图:
∵
∴
∴
∵
∴
∵
∴
∵、 分别平分 、
∴
∵在四边形中,
∴.
23.
(1)解:∵CE∥AD,
∴,
∴,
∵AB∥CD,
∴;
(2)解:∵平分,
∴,
∵,
∴.
24.
解:
(1)证明:如图,过点 A 作直线 MN,使 MN∥BC,,
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
∴∠BAC+∠B+∠C=180°.
(2)解:如图 2,
∵∠A+∠E=∠DME,∠G+∠D=∠ANG,∠C+∠F=∠BHC,
∵∠DME+∠ANG=∠BPH,
∴∠A+∠E+∠G+∠D=∠BPH,
∵∠B+∠BHC+∠BPH=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
25.
解:(1)正多边形每个内角的度数为.
;
;
正五边形的内角,;
正五边形的内角,.
(2)观察(1)中结论,
总结规律,则有.
(3)借助(2)中公式,有
,即
解得.
26.
解:(1)①证明:∵凸五边形的各条边都相等
∴
在、、、、中,
∴
∴
∴五边形是正五边形;
②解:若,五边形是正五边形,理由如下:
在、和中,
∴
∴,
在和中,
∴
∴,
∵四边形内角和为
∴
∴
∴,
∴
∴
同理:
∴五边形是正五边形;
(2)解:①若,则六边形是正六边形;假命题,理由如下:
如图3所示,∵凸六边形的各条边都相等
∴
在、和中,
∴
因此,如果都为相同的等腰直角三角形,符合题意
但,而正六边形的每个内角都为
∴六边形不是正六边形
故答案为:假;
②若,则六边形是正六边形;假命题;理由如下:
如图4所示:连接、、
在和中,
∴
∴
∵
∴
∴
在和中,
∴
∴
同理:
∴
由(2)①可知:六边形不是正六边形
故答案为:假.
一、单选题
1.下列多边形中,内角和等于的是( )
A. B. C. D.
2.十二边形的外角和为( )
A. B. C. D.
3.一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )
A.正方形 B.正六边形 C.正八边形 D.正十边形
4.一个多边形的内角和为900°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
5.六边形的内角和是( )
A.180° B.360° C.540° D.720°
6.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
7.下列命题是真命题的是( )
A.五边形的内角和是 B.三角形的任意两边之和大于第三边
C.内错角相等 D.三角形的重心是这个三角形的三条角平分线的交点
8.如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角( )
A. B. C. D.
9.如图,一束太阳光线平行照射在放置于地面的正六边形上,若,则的度数为( )
A. B. C. D.
10.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
二、填空题
11.若正n边形的一个外角为,则_____________.
12.五边形的内角和是________度.
13.正五边形的一个外角的大小为__________度.
14.若七边形的内角中有一个角为,则其余六个内角之和为________.
15.若正多边形的一个内角等于,则这个正多边形的边数是 ______.
16.如图,在正五边形ABCDE中,连接AC,则∠BAC的度数为_____.
17.如果一个正多边形的一个外角是60°,那么这个正多边形的边数是_____.
18.已知一个多边形的内角和为540°,则这个多边形是______边形.
19.如果正n边形的一个内角与一个外角的比是3:2,则_______.
20.如图所示,已知,正五边形的顶点、在射线上,顶点在射线上,则_________度.
三、解答题
21.一个多边形,它的内角和比外角和的4倍多,求这个多边形的边数及内角和度数.
22.如图,,,的平分线与的平分线交于点,求的度数.
23.如图,AB∥CD,平分,CE∥AD,.
(1)求的度数:
(2)若,求的度数.
24.
(1)叙述并证明三角形内角和定理(证明用图 1);
(2)如图 2 是七角星形,求∠A+∠B+∠C+∠D+∠E+∠F+∠G 的度数.
25.如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题.
将表格补充完整.
正多边形的边数 3 4 5 6
α的度数
观察上面表格中α的变化规律,角α与边数n的关系为 .
根据规律,当α=18°时,多边形边数n= .
26.我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
(1)已知凸五边形的各条边都相等.
①如图1,若,求证:五边形是正五边形;
②如图2,若,请判断五边形是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形的各条边都相等.
①若,则六边形是正六边形;( )
②若,则六边形是正六边形. ( )
答案
一、单选题
1.B
【分析】根据n边形内角和公式分别求解后,即可得到答案
解:A.三角形内角和是,故选项不符合题意;
B.四边形内角和为,故选项符合题意;
C.五边形内角和为,故选项不符合题意;
D.六边形内角和为,故选项不符合题意.
故选:B.
2.C
【分析】根据多边形的外角和为360°进行解答即可.
解:∵多边形的外角和为360°
∴十二边形的外角和是360°.
故选:C.
3.C
【分析】设这个外角是x°,则内角是3x°,根据内角与它相邻的外角互补列出方程求出外角的度数,根据多边形的外角和是360°即可求解.
解:∵一个正多边形每个内角与它相邻外角的度数比为3:1,
∴设这个外角是x°,则内角是3x°,
根据题意得:x+3x=180°,
解得:x=45°,
360°÷45°=8(边),
故选:C.
4.A
【分析】根据n边形的内角和是(n﹣2) 180°,列出方程即可求解.
解:根据n边形的内角和公式,得
(n﹣2) 180°=900°,
解得n=7,
∴这个多边形的边数是7,
故选:A.
5.D
【分析】根据多边形的内角和公式解答即可.
解:六边形的内角和是:;
故选:D.
6.C
【分析】进行平面镶嵌就是在同一顶点处的几个多边形的内角和应是,因此我们只需要验证是不是上面所给的几个正多边形的一个内角度数的整数倍即可.
解:A、等边三角形每个内角的度数为,,故该项不符合题意;
B、正方形的每个内角的度数为,,故该项不符合题意;
C、正五边形的每个内角的度数为,,故该项符合题意;
D、正六边形的每个内角的度数为,,故该项不符合题意;
故选:C.
7.B
【分析】根据相关概念逐项分析即可.
解:A、五边形的内角和是,故原命题为假命题,不符合题意;
B、三角形的任意两边之和大于第三边,原命题是真命题,符合题意;
C、两直线平行,内错角相等,故原命题为假命题,不符合题意;
D、三角形的重心是这个三角形的三条中线的交点,故原命题为假命题,不符合题意;
故选:B.
8.A
【分析】由正八边形的外角和为,结合正八边形的每一个外角都相等,再列式计算即可.
解:∵正八边形的外角和为,
∴,
故选A
9.B
【分析】如图,求出正六边形的一个内角和一个外角的度数,得到,平行线的性质,得到,三角形的外角的性质,得到,进而求出的度数.
解:如图:
∵正六边形的一个外角的度数为:,
∴正六边形的一个内角的度数为:,
即:,
∵一束太阳光线平行照射在放置于地面的正六边形上,,
∴,
∴,
∴;
故选B.
10.B
【分析】利用正n边形的外角和定理计算即可
解:如图,延长BA到点O,
∵六边形ABCDEF是正六边形,
∴∠FAO==60°,
∵五边形ABGHI是正五边形,
∴∠IAO==72°,
∴∠FAI=∠IAO-∠FAO=12°,
故选B.
二、填空题
11.5
【分析】正多边形的外角和为,每一个外角都相等,由此计算即可.
解:由题意知,,
故答案为:5.
12.540
【分析】根据n边形内角和为求解即可.
解:五边形的内角和是.
故答案为:540.
13.72
【分析】根据多边形的外角和是360°,依此即可求解.
解:正五边形的一个外角的度数为:,
故答案为:72.
14.
【分析】根据多边形的内角和公式即可得.
解:∵七边形的内角中有一个角为,
∴其余六个内角之和为,
故答案为:.
15.10
【分析】本题需先根据已知条件设出正多边形的边数,再根据正多边形的计算公式得出结果即可.
解:设这个正多边形是正n边形,根据题意得:
,
解得:.
故答案为:10.
16.36°
【分析】首先利用多边形的内角和公式求得正五边形的内角和,再求得每个内角的度数,利用等腰三角形的性质可得∠BAC的度数.
解:正五边形内角和:(5﹣2)×180°=3×180°=540°
∴,
∴ .
故答案为36°.
17.6
解:根据多边形的外角和等于360°和正多边形的每一个外角都相等,得多边形的边数为360°÷60°=6.
故答案为:6.
18.5
解:设这个多边形是n边形,由题意得,
(n-2) ×180°=540°,解之得,n=5.
19.5
【分析】设多边形的一个内角为3x度,一个外角则为2x度,求得外角的度数,然后根据多边形的外角和为360°,进而求出n的值.
解:∵正边形的一个内角度数与其外角度数的比是3:2,
∴设多边形的一个内角为3x度,一个外角则为2x度,
∴3x+2x=180°,
解得x=36°,
∴一个外角为2x=72°,
360°÷72°=5,
∴n=5,
故答案为:5.
20.48
【分析】是正五边形的一个外角,利用多边形外交和360°算出一个外角,再利用的内角和180°,即可算出
解:∵四边形ABCDE是正五边形,是一个外角
∴
在中:
故答案为:48
三、解答题
21.
解:根据题意,得
(n 2) 180°=360°×4+180°,
解得:n=11.
360°×4+180°=1620°
则这个多边形的边数是11,内角和度数是1620度.
22.
解:过点作,如图:
∵
∴
∴
∵
∴
∵
∴
∵、 分别平分 、
∴
∵在四边形中,
∴.
23.
(1)解:∵CE∥AD,
∴,
∴,
∵AB∥CD,
∴;
(2)解:∵平分,
∴,
∵,
∴.
24.
解:
(1)证明:如图,过点 A 作直线 MN,使 MN∥BC,,
∵MN∥BC,
∴∠B=∠MAB,∠C=∠NAC(两直线平行,内错角相等)
∵∠MAB+∠NAC+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180°(等量代换)
∴∠BAC+∠B+∠C=180°.
(2)解:如图 2,
∵∠A+∠E=∠DME,∠G+∠D=∠ANG,∠C+∠F=∠BHC,
∵∠DME+∠ANG=∠BPH,
∴∠A+∠E+∠G+∠D=∠BPH,
∵∠B+∠BHC+∠BPH=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
25.
解:(1)正多边形每个内角的度数为.
;
;
正五边形的内角,;
正五边形的内角,.
(2)观察(1)中结论,
总结规律,则有.
(3)借助(2)中公式,有
,即
解得.
26.
解:(1)①证明:∵凸五边形的各条边都相等
∴
在、、、、中,
∴
∴
∴五边形是正五边形;
②解:若,五边形是正五边形,理由如下:
在、和中,
∴
∴,
在和中,
∴
∴,
∵四边形内角和为
∴
∴
∴,
∴
∴
同理:
∴五边形是正五边形;
(2)解:①若,则六边形是正六边形;假命题,理由如下:
如图3所示,∵凸六边形的各条边都相等
∴
在、和中,
∴
因此,如果都为相同的等腰直角三角形,符合题意
但,而正六边形的每个内角都为
∴六边形不是正六边形
故答案为:假;
②若,则六边形是正六边形;假命题;理由如下:
如图4所示:连接、、
在和中,
∴
∴
∵
∴
∴
在和中,
∴
∴
同理:
∴
由(2)①可知:六边形不是正六边形
故答案为:假.
