2024年吉林省松原市前郭县南部学区中考数学六模试卷(含解析)
文档属性
| 名称 | 2024年吉林省松原市前郭县南部学区中考数学六模试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 07:32:15 | ||
图片预览



文档简介
2024年吉林省松原市前郭县南部学区中考数学六模试卷
一、选择题(每小题2分,共12分)
1.(2分)的相反数是( )
A. B. C. D.3
2.(2分)水质指纹污染溯源技术是一项水环境监管技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分子的直径约有0.0000004mm,数据0.0000004用科学记数法表示为4×10a,则a的值为( )
A.﹣6 B.﹣7 C.﹣8 D.7
3.(2分)下列图形中,能折叠成正方体的是( )
A.
B.
C.
D.
4.(2分)化简x6÷x2的结果是( )
A.x8 B.x4 C.x3 D.x
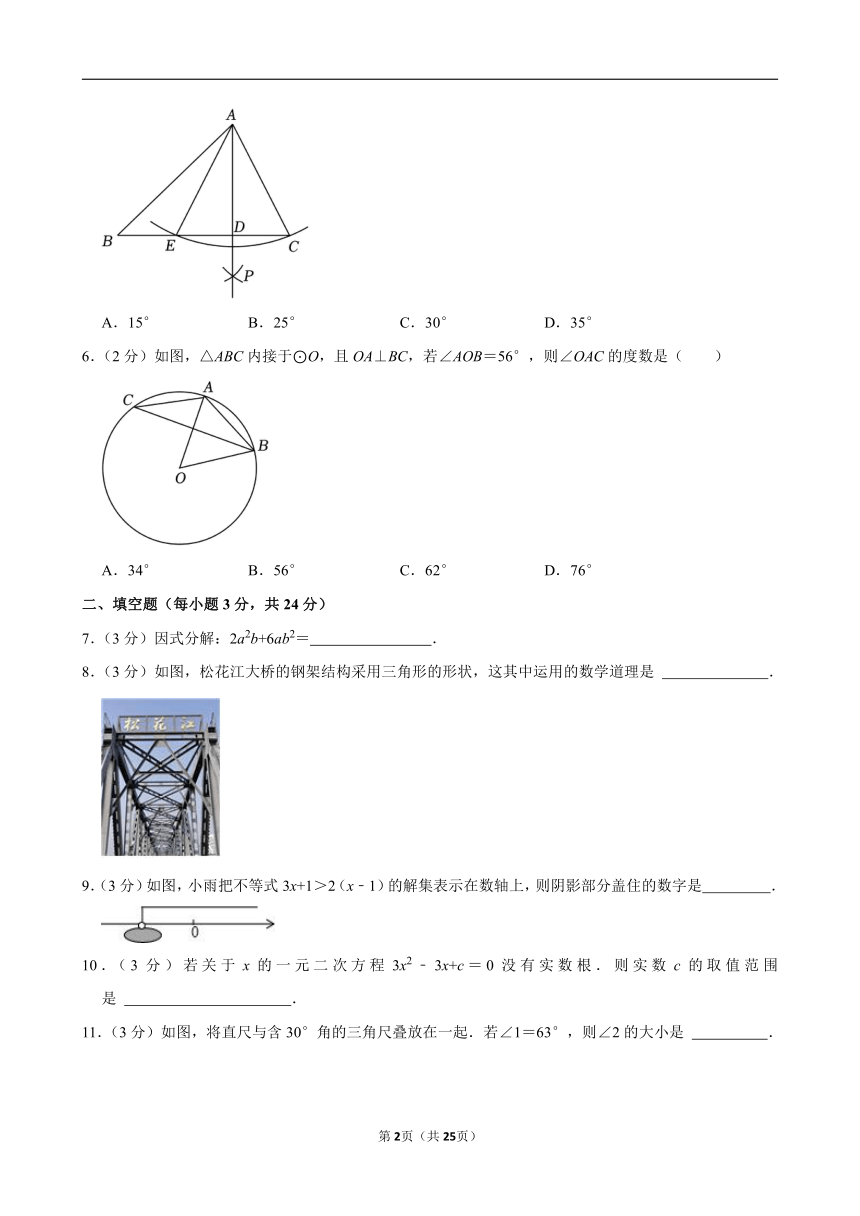
5.(2分)如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E和点C为圆心、大于的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,∠C=2∠CAD,则∠BAE的度数为( )
A.15° B.25° C.30° D.35°
6.(2分)如图,△ABC内接于⊙O,且OA⊥BC,若∠AOB=56°,则∠OAC的度数是( )
A.34° B.56° C.62° D.76°
二、填空题(每小题3分,共24分)
7.(3分)因式分解:2a2b+6ab2= .
8.(3分)如图,松花江大桥的钢架结构采用三角形的形状,这其中运用的数学道理是 .
9.(3分)如图,小雨把不等式3x+1>2(x﹣1)的解集表示在数轴上,则阴影部分盖住的数字是 .
10.(3分)若关于x的一元二次方程3x2﹣3x+c=0没有实数根.则实数c的取值范围是 .
11.(3分)如图,将直尺与含30°角的三角尺叠放在一起.若∠1=63°,则∠2的大小是 .
12.(3分)一个三层折叠花架如图所示,已知AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则BF的长为 cm.
13.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
14.(3分)如图所示,在矩形ABCD中,如图AB<BC,以点C为圆心,CB的长为半径的圆分别交AD边于点E,交CD边的延长线于点F.若AE=DF,的长为π,则DE的长为 .
三、解答题(每小题5分,共20分)
15.(5分)计算:(﹣1+3)×2+4÷(﹣2)﹣20240.
16.(5分)已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC.若DE=CF,连结EF.求证:四边形ABFE是菱形.
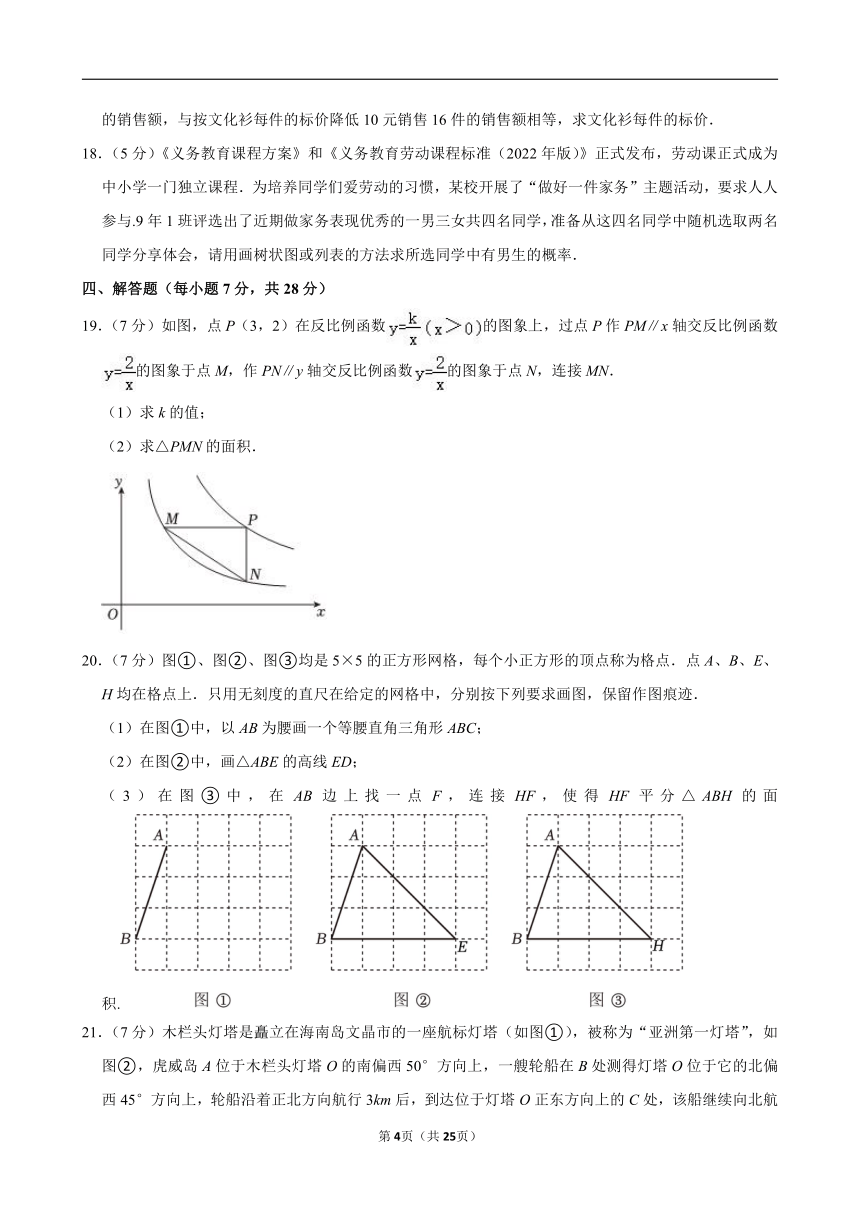
17.(5分)2024年2月,第十四届全国冬季运动会在内蒙古自治区举办,吉祥物蒙古彩娃“安达”和“赛努”深受人民喜爱.某商店在销售一种印有蒙古彩娃的文化衫时,按文化衫每件标价的8折销售15件的销售额,与按文化衫每件的标价降低10元销售16件的销售额相等,求文化衫每件的标价.
18.(5分)《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学一门独立课程.为培养同学们爱劳动的习惯,某校开展了“做好一件家务”主题活动,要求人人参与.9年1班评选出了近期做家务表现优秀的一男三女共四名同学,准备从这四名同学中随机选取两名同学分享体会,请用画树状图或列表的方法求所选同学中有男生的概率.
四、解答题(每小题7分,共28分)
19.(7分)如图,点P(3,2)在反比例函数的图象上,过点P作PM∥x轴交反比例函数的图象于点M,作PN∥y轴交反比例函数的图象于点N,连接MN.
(1)求k的值;
(2)求△PMN的面积.
20.(7分)图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点.点A、B、E、H均在格点上.只用无刻度的直尺在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中,以AB为腰画一个等腰直角三角形ABC;
(2)在图②中,画△ABE的高线ED;
(3)在图③中,在AB边上找一点F,连接HF,使得HF平分△ABH的面积.
21.(7分)木栏头灯塔是矗立在海南岛文晶市的一座航标灯塔(如图①),被称为“亚洲第一灯塔”,如图②,虎威岛A位于木栏头灯塔O的南偏西50°方向上,一艘轮船在B处测得灯塔O位于它的北偏西45°方向上,轮船沿着正北方向航行3km后,到达位于灯塔O正东方向上的C处,该船继续向北航行至直线AO上的点D处.
(1)填空:∠BOC= 度,∠D= 度;
(2)求点D到灯塔O的距离(参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73.结果精确到小数点后一位).
22.(7分)某校举办“跨学科综合实践活动”,五名评委对每组同学的参赛作品进行打分.对参加比赛的甲、乙、丙三个组参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、丙两组参赛作品得分的折线图:
b.在给乙组参赛作品的打分中,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
c.甲、乙、丙三个组参赛作品得分的平均数:
甲组 乙组 丙组
88 90 n
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是 组(填“甲”或“丙”);
(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组,请说明理由.
五、解答题(每小题8分,共16分)
23.(8分)蓄电池发展水平是制约新能源汽车发展的关键要素.小明爸爸根据自家电动汽车仪表显示,感觉蓄电池充满电后,用前半部分电量所行驶的路程,总要比用后半部分电量行驶的路程更远一些.于是小明细心观察了充满电后汽车的行驶情况,并将蓄电池剩余电量y(千瓦时)和已行驶路程x(千米)的相关数据,用函数图象表示如下.
(1)电池充满电时的电量为 千瓦时;
(2)求BC所对应的函数关系式(不要求写出自变量的取值范围);
(3)在电量允许的情况下,如果在某段连续行驶时间里,汽车消耗了10千瓦时的电量,直接写出这段时间连续行驶路程s的取值范围.
24.(8分)综合与探究
问题情境:数学课上,同学们以直角三角形纸片为背景进行探究性活动.如图1,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转,使线段AB的对应线段A'B'恰好经过点B,得到图2,线段A'C与AB相交于点D.
初步分析:(1)判断△CBB'的形状,并说明理由;
深入探究:(2)乐学组的同学将图2中的△BDC沿射线BA的方向平移得到△EFG(点E,F,G分别是点B,D,C的对应点),线段EG,FG分别与边AC相交于点M,N.
①如图3,当点M恰好是线段EG的中点时,他们发现MN=FN,请证明这个结论;
②若BC=4,当点N恰好是线段AM的中点时,请直接写出△BDC平移的距离.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠ACB=90°,BC=2,AC=4,CD是边AB上的中线,动点P从点C出发,以每秒个单位长度的速度沿线段CD向终点D运动.过点P作PQ⊥AC于点Q,以PQ为边作等腰直角三角形PQN,∠QPN=90°,使点N、C始终在PQ的两侧.设点P的运动时间为t(s)(t>0),△PQN与△ADC重合部分图形的面积为S.
(1)用含t的代数式表示DP的长;
(2)当点N落在边AB上时,求t的值;
(3)求S关于t的函数关系式,并写出自变量t的取值范围.
26.(10分)如图,在平面直角坐标系中,抛物线y=x2+ax﹣3(a为常数)经过点(﹣1,0).
(1)求此抛物线对应的函数解析式;
(2)点P在此抛物线上,其横坐标为m.
①当点P在y轴右侧,且点P到x轴的距离等于3,求点P的坐标;
②若点Q也在此抛物线上,其横坐标为m+1,当点P、Q之间(含点P、Q)的抛物线上恰好只有一个点到x轴的距离等于5时,请直接写出m的取值范围;
(3)设点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),连接EF,当抛物线y=x2+ax﹣3(a为常数)和线段EF只有一个公共点时,直接写出n的取值范围.
参考答案与试题解析
一、选择题(每小题2分,共12分)
1.(2分)的相反数是( )
A. B. C. D.3
【解答】解:的相反数是,
故选:C.
2.(2分)水质指纹污染溯源技术是一项水环境监管技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分子的直径约有0.0000004mm,数据0.0000004用科学记数法表示为4×10a,则a的值为( )
A.﹣6 B.﹣7 C.﹣8 D.7
【解答】解:∵0.0000004=4×10﹣7,
∴a=﹣7.
故选:B.
3.(2分)下列图形中,能折叠成正方体的是( )
A.
B.
C.
D.
【解答】解:A.折叠后有一行两个面无法折起来,缺少一个面,故本选项不合题意;
B.折叠后是三棱柱,故本选项不合题意;
C.折叠后能折叠成正方体,故本选项符合题意;
D.折叠后有一行两个面无法折起来,而且都缺少一个面有两个面重合,不能折成正方体,故本选项不合题意;
故选:C.
4.(2分)化简x6÷x2的结果是( )
A.x8 B.x4 C.x3 D.x
【解答】解:x6÷x2=x6﹣2=x4.
故选:B.
5.(2分)如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E和点C为圆心、大于的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,∠C=2∠CAD,则∠BAE的度数为( )
A.15° B.25° C.30° D.35°
【解答】解:由题意可知,AP是EC的垂直平分线,
∴AD⊥BC,DE=CD,
∴△ADE≌△ADC(SAS),
∴∠EAD=∠CAD,∠C=∠AED,
∴∠EAC=2∠CAD,
∵∠C=2∠CAD,
∴∠C=∠EAC=∠AED,
∴△AEC是等边三角形,
∴∠C=∠EAC=∠AED=60°,
在△ABC中,∠B=45°,∠C=60°,
∴∠BAC=180°﹣45°﹣60°=75°,
∴∠BAE=75°﹣60°=15°.
故选:A.
6.(2分)如图,△ABC内接于⊙O,且OA⊥BC,若∠AOB=56°,则∠OAC的度数是( )
A.34° B.56° C.62° D.76°
【解答】解:如图,设OA⊥BC于D,
∵OA⊥BC,
∴∠ADC=90°,
∵∠AOB=56°,
∴∠C=AOB=28°,
∴∠OAC=180°﹣∠C﹣∠ADC=180°﹣28°﹣90°=62°,
故选:C.
二、填空题(每小题3分,共24分)
7.(3分)因式分解:2a2b+6ab2= 2ab(a+3b) .
【解答】解:2a2b+6ab2=2ab(a+3b).
故答案为:2ab(a+3b).
8.(3分)如图,松花江大桥的钢架结构采用三角形的形状,这其中运用的数学道理是 三角形的稳定性 .
【解答】解:松花江大桥的钢架结构采用三角形的形状,其中的数学道理是三角形的稳定性,
故答案为:三角形的稳定性.
9.(3分)如图,小雨把不等式3x+1>2(x﹣1)的解集表示在数轴上,则阴影部分盖住的数字是 ﹣3 .
【解答】解:去括号,得
3x+1>2x﹣2,
移项、合并同类项,得
x>﹣3,
故答案为:﹣3.
10.(3分)若关于x的一元二次方程3x2﹣3x+c=0没有实数根.则实数c的取值范围是 c> .
【解答】解:∵一元二次方程3x2﹣3x+c=0没有实数根,
∴Δ=(﹣3)2﹣4×3×c<0,
∴c>.
故答案为:c>.
11.(3分)如图,将直尺与含30°角的三角尺叠放在一起.若∠1=63°,则∠2的大小是 57° .
【解答】解:如图,
由题意得∠ABC=60°,
∵∠1=63°,
∴∠CBD=180°﹣∠1﹣∠ABC=57°,
由直尺可得:AC∥BD,
∴∠2=∠CBD=57°.
故答案为:57°.
12.(3分)一个三层折叠花架如图所示,已知AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则BF的长为 120 cm.
【解答】解:∵AB∥CD∥EF,
∴=,
∵AC=30cm,CE=50cm,BD=45cm,
∴=,
解得:DF=75,
则BF=BD+DF=45+75=120(cm),
故答案为:120.
13.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
【解答】解:由题意可得:
,
故答案为:.
14.(3分)如图所示,在矩形ABCD中,如图AB<BC,以点C为圆心,CB的长为半径的圆分别交AD边于点E,交CD边的延长线于点F.若AE=DF,的长为π,则DE的长为 2 .
【解答】解:连接CE,则CB=CE=CF,
设CB=R,
∵四边形ABCD是矩形,
∴CE=CF=DA,
∵AE=DF,
∴DE=DC,
∴DCE=45°,
∵的长为π,
∴=π,
解得R=4,
在Rt△DCE中,
DE=CE sin 45°=4×B=2.
故答案为:2.
三、解答题(每小题5分,共20分)
15.(5分)计算:(﹣1+3)×2+4÷(﹣2)﹣20240.
【解答】解:(﹣1+3)×2+4÷(﹣2)﹣20240
=2×2+4÷(﹣2)﹣1
=4+(﹣2)+(﹣1)
=1.
16.(5分)已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC.若DE=CF,连结EF.求证:四边形ABFE是菱形.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵DE=CF,
∴AE=BF,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
17.(5分)2024年2月,第十四届全国冬季运动会在内蒙古自治区举办,吉祥物蒙古彩娃“安达”和“赛努”深受人民喜爱.某商店在销售一种印有蒙古彩娃的文化衫时,按文化衫每件标价的8折销售15件的销售额,与按文化衫每件的标价降低10元销售16件的销售额相等,求文化衫每件的标价.
【解答】解:设文化衫每件的标价为x元,
根据题意得:15×0.8x=16(x﹣10),
解得:x=40.
答:文化衫每件的标价为40元.
18.(5分)《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学一门独立课程.为培养同学们爱劳动的习惯,某校开展了“做好一件家务”主题活动,要求人人参与.9年1班评选出了近期做家务表现优秀的一男三女共四名同学,准备从这四名同学中随机选取两名同学分享体会,请用画树状图或列表的方法求所选同学中有男生的概率.
【解答】解:列表如下:
男 女 女 女
男 (男,女) (男,女) (男,女)
女 (女,男) (女,女) (女,女)
女 (女,男) (女,女) (女,女)
女 (女,男) (女,女) (女,女)
共有12种等可能的结果,其中所选同学中有男生的结果有6种,
∴所选同学中有男生的概率为=.
四、解答题(每小题7分,共28分)
19.(7分)如图,点P(3,2)在反比例函数的图象上,过点P作PM∥x轴交反比例函数的图象于点M,作PN∥y轴交反比例函数的图象于点N,连接MN.
(1)求k的值;
(2)求△PMN的面积.
【解答】解:(1)∵点P(3,2)在反比例函数的图象上,
∴k=2×3=6.
(2)设点P(m,),则M(,),N(m,)
∴S△PMN=
=×)
=×
=.
20.(7分)图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点.点A、B、E、H均在格点上.只用无刻度的直尺在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中,以AB为腰画一个等腰直角三角形ABC;
(2)在图②中,画△ABE的高线ED;
(3)在图③中,在AB边上找一点F,连接HF,使得HF平分△ABH的面积.
【解答】解:(1)如图①中,△ABC即为所求(答案不唯一);
(2)如图②中,线段ED即为所求;
(3)如图③中,线段HF即为所求.
21.(7分)木栏头灯塔是矗立在海南岛文晶市的一座航标灯塔(如图①),被称为“亚洲第一灯塔”,如图②,虎威岛A位于木栏头灯塔O的南偏西50°方向上,一艘轮船在B处测得灯塔O位于它的北偏西45°方向上,轮船沿着正北方向航行3km后,到达位于灯塔O正东方向上的C处,该船继续向北航行至直线AO上的点D处.
(1)填空:∠BOC= 45 度,∠D= 50 度;
(2)求点D到灯塔O的距离(参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73.结果精确到小数点后一位).
【解答】解:(1)由题意可知,OC⊥BD,
∵∠CBO=45°,
∴∠BOC=90°﹣∠CBO=45°,
∴∠COD=180°﹣50°﹣90°=40°,
∴∠D=90°﹣∠COD=50°,
故答案为:45,50;
(2)由题意可知:BC=3km,
在Rt△BOC中,
∠CBO=45°,
∴OC=BC=3km,
在Rt△DOC中,∠D=50°,
∴OD==≈3.9(km),
答:点D到灯塔O的距离约为3.9km.
22.(7分)某校举办“跨学科综合实践活动”,五名评委对每组同学的参赛作品进行打分.对参加比赛的甲、乙、丙三个组参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、丙两组参赛作品得分的折线图:
b.在给乙组参赛作品的打分中,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
c.甲、乙、丙三个组参赛作品得分的平均数:
甲组 乙组 丙组
88 90 n
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是 丙 组(填“甲”或“丙”);
(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组,请说明理由.
【解答】解:(1)由题意得,n==90;
(2)由折线统计图可知,丙组数据的波动比甲组的小,所以五位评委评价更“一致”的是丙组.
故答案为:丙;
(3)由题意可知,乙组和丙组的平均数均为90分,比甲组的平均数88分高,所以从乙组和丙组推荐一个小组的作品到区里参加比赛,
又因为乙组的最低分比丙组的最低分高,所以应该推荐乙组.
五、解答题(每小题8分,共16分)
23.(8分)蓄电池发展水平是制约新能源汽车发展的关键要素.小明爸爸根据自家电动汽车仪表显示,感觉蓄电池充满电后,用前半部分电量所行驶的路程,总要比用后半部分电量行驶的路程更远一些.于是小明细心观察了充满电后汽车的行驶情况,并将蓄电池剩余电量y(千瓦时)和已行驶路程x(千米)的相关数据,用函数图象表示如下.
(1)电池充满电时的电量为 60 千瓦时;
(2)求BC所对应的函数关系式(不要求写出自变量的取值范围);
(3)在电量允许的情况下,如果在某段连续行驶时间里,汽车消耗了10千瓦时的电量,直接写出这段时间连续行驶路程s的取值范围.
【解答】解:(1)观察函数图象可知,电池充满电的电量为60千瓦时;
故答案为:60;
(2)设BC所对应的函数关系式为 y=kx+b,
把(150,35)和(200,10)代入得:
,
解得,
∴BC所对应的函数关系式为y=﹣x+110;
(3)当在AB段消耗了10千瓦时的电量时,s=×10=60(千米);
当在BC段消耗了10千瓦时的电量时,s=×10=20(千米);
∴20≤s≤60.
24.(8分)综合与探究
问题情境:数学课上,同学们以直角三角形纸片为背景进行探究性活动.如图1,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转,使线段AB的对应线段A'B'恰好经过点B,得到图2,线段A'C与AB相交于点D.
初步分析:(1)判断△CBB'的形状,并说明理由;
深入探究:(2)乐学组的同学将图2中的△BDC沿射线BA的方向平移得到△EFG(点E,F,G分别是点B,D,C的对应点),线段EG,FG分别与边AC相交于点M,N.
①如图3,当点M恰好是线段EG的中点时,他们发现MN=FN,请证明这个结论;
②若BC=4,当点N恰好是线段AM的中点时,请直接写出△BDC平移的距离.
【解答】(1)解:△CBB′是等边三角形,理由如下:
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
由旋转得:BC=B′C,∠B′=∠ABC=60°,
∴△CBB′是等边三角形;
(2)①证明:如图3,连接EN,
∵△CBB′是等边三角形,
∴∠BCB′=60°,
由旋转得:∠A′CB′=∠ACB=90°,
∴∠BCD=∠ACB﹣∠BCB′
=90°﹣60°
=30°,
∴∠BDC=180°﹣∠BCD﹣∠CBD=90°,
由平移得:∠G=∠BCD=30°,∠EFG=∠BDC=90°,EG∥BC,
∴EF=EG,∠EMN=∠ACB=90°,
∵点M恰好是线段EG的中点,
∴EM=EG,
∴EF=EM,
在Rt△EFN和Rt△EMN中,
,
∴Rt△EFN≌Rt△EMN(HL),
∴MN=FN;
②解:设MN=x,
∵N是AM的中点,
∴AN=x,AM=2x,
由①得:GN=2MN=2x,AE=2EM,AB=2BC=8,
∴MG==x,
∵EM2+AM2=AE2,
∴EM2+(2x)2=(2EM)2,
解得:EM=x,
∴EG=EM+MG=x+x=x,
由平移得:EG=BC=4,
解得:x=.
∴EM=×=,
∴AE=2EM=,
∴BE=AB﹣AE=8﹣=,
故△BDC平移的距离为.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠ACB=90°,BC=2,AC=4,CD是边AB上的中线,动点P从点C出发,以每秒个单位长度的速度沿线段CD向终点D运动.过点P作PQ⊥AC于点Q,以PQ为边作等腰直角三角形PQN,∠QPN=90°,使点N、C始终在PQ的两侧.设点P的运动时间为t(s)(t>0),△PQN与△ADC重合部分图形的面积为S.
(1)用含t的代数式表示DP的长;
(2)当点N落在边AB上时,求t的值;
(3)求S关于t的函数关系式,并写出自变量t的取值范围.
【解答】解:(1)∵∠ACB=90°,BC=2,AC=4,
∴AB===2,
∵CD是边AB的中线,
∴DC=AB=,
∵动点P从点C出发,以每秒个单位长度的速度沿折线CD﹣DB向终点B运动,
∴PC=t,
∴DP=﹣t,
(2)当点N落在AB边上时,点P只能在CD上,
∵CD是直角三角形ABC的中线,则△ACD为等腰三角形,
则∠DCA=∠A=α,
则tanA==tanα,则sinα=,cosα=,
过点D作DH⊥NP于点H,
由题意得,△NPD为等腰三角形,且∠DNP=∠A=α,
则NP=2HP=2PDcosα=2×(﹣t)×=4﹣4t,
而PQ=PCsinα=t ,
∴t=4﹣4t,
解得:t=;
(3)当0<t时,由(2)知PQ=t,
∴△PQN与△ADC重合部分图形的面积S=;
当<t<1时,如图,过点H作HF⊥PN于点F,
由(2)知PE=4﹣4t,
∴EN=PN﹣PE=5t﹣4,
∵tanA=tan∠FEH=,
∴,
∴,即,
∴HF=,
∴=,
∴△PQN与△ADC重合部分图形的面积S=S△PQN﹣S△ENH==﹣,
即.
26.(10分)如图,在平面直角坐标系中,抛物线y=x2+ax﹣3(a为常数)经过点(﹣1,0).
(1)求此抛物线对应的函数解析式;
(2)点P在此抛物线上,其横坐标为m.
①当点P在y轴右侧,且点P到x轴的距离等于3,求点P的坐标;
②若点Q也在此抛物线上,其横坐标为m+1,当点P、Q之间(含点P、Q)的抛物线上恰好只有一个点到x轴的距离等于5时,请直接写出m的取值范围;
(3)设点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),连接EF,当抛物线y=x2+ax﹣3(a为常数)和线段EF只有一个公共点时,直接写出n的取值范围.
【解答】解:(1)由题意,把点(﹣1,0)代入抛物线 y=x2+ax﹣3,
∴0=12﹣a﹣3.
∴a=﹣2.
∴抛物线的函数解析式为y=x2﹣2x﹣3.
(2)①由题意,设点P的坐标为(m,3),
∵P到x轴的距离等于3,即|y|=3,
∴y=3或y=﹣3.
当y=3时,3=m2﹣2m﹣3,
∴ 或 .
当y=﹣3时.﹣3=m2﹣2m﹣3,
∴m=0或m=2.
∵P点在y轴右侧,
∴m>0.
∴ 或m=2.
∴P ,3)或 (2,﹣3).
②∵P、Q之间只有一个点到x轴的距离为5,
∴y1=5,即5=m2﹣2m﹣3.
∴m=﹣2或m=4.
∵点Q的横坐标为m+1,且点P、Q之间(含P、Q)的抛物线上恰好只有一个点到x轴的距离等于5,
∴﹣3≤m≤﹣2或3≤m≤4.
(3))∵点E的坐标为(n﹣2,n﹣2),
∴yE=n﹣2,xE=n﹣2,即yE=xE,
∴点E在直线y=x上,
∵点F的坐标为(n+2,n﹣2),
∴同理可求出点F在直线y=x﹣4上,
结合平移可知:直线y=x向右平移4个单位即可得到直线y=x﹣4,
设直线y=x、y=x﹣4与抛物线y=x2﹣2x﹣3交于点A、B、C、D四点,
∵点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),
∴EF=n+2﹣(n﹣2)=4,且线段EF在直线y=n﹣2上,
∴DF∥x轴,
如图,
联立:,
解得:,.
∴,.
联立:.
解得:,.
∴,.
结合图形可知:当点E在点A与点B之间(含点A,不含点B)或者当点F在点C与点D之间(含点D,不含点C)时,抛物线y=x2﹣2x﹣3和线段EF只有一个有公共点,
∴<n﹣2≤或<n+2≤.
∴<n≤或<n≤.
第1页(共1页)
一、选择题(每小题2分,共12分)
1.(2分)的相反数是( )
A. B. C. D.3
2.(2分)水质指纹污染溯源技术是一项水环境监管技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分子的直径约有0.0000004mm,数据0.0000004用科学记数法表示为4×10a,则a的值为( )
A.﹣6 B.﹣7 C.﹣8 D.7
3.(2分)下列图形中,能折叠成正方体的是( )
A.
B.
C.
D.
4.(2分)化简x6÷x2的结果是( )
A.x8 B.x4 C.x3 D.x
5.(2分)如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E和点C为圆心、大于的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,∠C=2∠CAD,则∠BAE的度数为( )
A.15° B.25° C.30° D.35°
6.(2分)如图,△ABC内接于⊙O,且OA⊥BC,若∠AOB=56°,则∠OAC的度数是( )
A.34° B.56° C.62° D.76°
二、填空题(每小题3分,共24分)
7.(3分)因式分解:2a2b+6ab2= .
8.(3分)如图,松花江大桥的钢架结构采用三角形的形状,这其中运用的数学道理是 .
9.(3分)如图,小雨把不等式3x+1>2(x﹣1)的解集表示在数轴上,则阴影部分盖住的数字是 .
10.(3分)若关于x的一元二次方程3x2﹣3x+c=0没有实数根.则实数c的取值范围是 .
11.(3分)如图,将直尺与含30°角的三角尺叠放在一起.若∠1=63°,则∠2的大小是 .
12.(3分)一个三层折叠花架如图所示,已知AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则BF的长为 cm.
13.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
14.(3分)如图所示,在矩形ABCD中,如图AB<BC,以点C为圆心,CB的长为半径的圆分别交AD边于点E,交CD边的延长线于点F.若AE=DF,的长为π,则DE的长为 .
三、解答题(每小题5分,共20分)
15.(5分)计算:(﹣1+3)×2+4÷(﹣2)﹣20240.
16.(5分)已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC.若DE=CF,连结EF.求证:四边形ABFE是菱形.
17.(5分)2024年2月,第十四届全国冬季运动会在内蒙古自治区举办,吉祥物蒙古彩娃“安达”和“赛努”深受人民喜爱.某商店在销售一种印有蒙古彩娃的文化衫时,按文化衫每件标价的8折销售15件的销售额,与按文化衫每件的标价降低10元销售16件的销售额相等,求文化衫每件的标价.
18.(5分)《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学一门独立课程.为培养同学们爱劳动的习惯,某校开展了“做好一件家务”主题活动,要求人人参与.9年1班评选出了近期做家务表现优秀的一男三女共四名同学,准备从这四名同学中随机选取两名同学分享体会,请用画树状图或列表的方法求所选同学中有男生的概率.
四、解答题(每小题7分,共28分)
19.(7分)如图,点P(3,2)在反比例函数的图象上,过点P作PM∥x轴交反比例函数的图象于点M,作PN∥y轴交反比例函数的图象于点N,连接MN.
(1)求k的值;
(2)求△PMN的面积.
20.(7分)图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点.点A、B、E、H均在格点上.只用无刻度的直尺在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中,以AB为腰画一个等腰直角三角形ABC;
(2)在图②中,画△ABE的高线ED;
(3)在图③中,在AB边上找一点F,连接HF,使得HF平分△ABH的面积.
21.(7分)木栏头灯塔是矗立在海南岛文晶市的一座航标灯塔(如图①),被称为“亚洲第一灯塔”,如图②,虎威岛A位于木栏头灯塔O的南偏西50°方向上,一艘轮船在B处测得灯塔O位于它的北偏西45°方向上,轮船沿着正北方向航行3km后,到达位于灯塔O正东方向上的C处,该船继续向北航行至直线AO上的点D处.
(1)填空:∠BOC= 度,∠D= 度;
(2)求点D到灯塔O的距离(参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73.结果精确到小数点后一位).
22.(7分)某校举办“跨学科综合实践活动”,五名评委对每组同学的参赛作品进行打分.对参加比赛的甲、乙、丙三个组参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、丙两组参赛作品得分的折线图:
b.在给乙组参赛作品的打分中,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
c.甲、乙、丙三个组参赛作品得分的平均数:
甲组 乙组 丙组
88 90 n
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是 组(填“甲”或“丙”);
(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组,请说明理由.
五、解答题(每小题8分,共16分)
23.(8分)蓄电池发展水平是制约新能源汽车发展的关键要素.小明爸爸根据自家电动汽车仪表显示,感觉蓄电池充满电后,用前半部分电量所行驶的路程,总要比用后半部分电量行驶的路程更远一些.于是小明细心观察了充满电后汽车的行驶情况,并将蓄电池剩余电量y(千瓦时)和已行驶路程x(千米)的相关数据,用函数图象表示如下.
(1)电池充满电时的电量为 千瓦时;
(2)求BC所对应的函数关系式(不要求写出自变量的取值范围);
(3)在电量允许的情况下,如果在某段连续行驶时间里,汽车消耗了10千瓦时的电量,直接写出这段时间连续行驶路程s的取值范围.
24.(8分)综合与探究
问题情境:数学课上,同学们以直角三角形纸片为背景进行探究性活动.如图1,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转,使线段AB的对应线段A'B'恰好经过点B,得到图2,线段A'C与AB相交于点D.
初步分析:(1)判断△CBB'的形状,并说明理由;
深入探究:(2)乐学组的同学将图2中的△BDC沿射线BA的方向平移得到△EFG(点E,F,G分别是点B,D,C的对应点),线段EG,FG分别与边AC相交于点M,N.
①如图3,当点M恰好是线段EG的中点时,他们发现MN=FN,请证明这个结论;
②若BC=4,当点N恰好是线段AM的中点时,请直接写出△BDC平移的距离.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠ACB=90°,BC=2,AC=4,CD是边AB上的中线,动点P从点C出发,以每秒个单位长度的速度沿线段CD向终点D运动.过点P作PQ⊥AC于点Q,以PQ为边作等腰直角三角形PQN,∠QPN=90°,使点N、C始终在PQ的两侧.设点P的运动时间为t(s)(t>0),△PQN与△ADC重合部分图形的面积为S.
(1)用含t的代数式表示DP的长;
(2)当点N落在边AB上时,求t的值;
(3)求S关于t的函数关系式,并写出自变量t的取值范围.
26.(10分)如图,在平面直角坐标系中,抛物线y=x2+ax﹣3(a为常数)经过点(﹣1,0).
(1)求此抛物线对应的函数解析式;
(2)点P在此抛物线上,其横坐标为m.
①当点P在y轴右侧,且点P到x轴的距离等于3,求点P的坐标;
②若点Q也在此抛物线上,其横坐标为m+1,当点P、Q之间(含点P、Q)的抛物线上恰好只有一个点到x轴的距离等于5时,请直接写出m的取值范围;
(3)设点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),连接EF,当抛物线y=x2+ax﹣3(a为常数)和线段EF只有一个公共点时,直接写出n的取值范围.
参考答案与试题解析
一、选择题(每小题2分,共12分)
1.(2分)的相反数是( )
A. B. C. D.3
【解答】解:的相反数是,
故选:C.
2.(2分)水质指纹污染溯源技术是一项水环境监管技术,被称为水环境治理的“福尔摩斯”,经测算,一个水分子的直径约有0.0000004mm,数据0.0000004用科学记数法表示为4×10a,则a的值为( )
A.﹣6 B.﹣7 C.﹣8 D.7
【解答】解:∵0.0000004=4×10﹣7,
∴a=﹣7.
故选:B.
3.(2分)下列图形中,能折叠成正方体的是( )
A.
B.
C.
D.
【解答】解:A.折叠后有一行两个面无法折起来,缺少一个面,故本选项不合题意;
B.折叠后是三棱柱,故本选项不合题意;
C.折叠后能折叠成正方体,故本选项符合题意;
D.折叠后有一行两个面无法折起来,而且都缺少一个面有两个面重合,不能折成正方体,故本选项不合题意;
故选:C.
4.(2分)化简x6÷x2的结果是( )
A.x8 B.x4 C.x3 D.x
【解答】解:x6÷x2=x6﹣2=x4.
故选:B.
5.(2分)如图,在△ABC中,以点A为圆心,AC的长为半径作弧,与BC交于点E,分别以点E和点C为圆心、大于的长为半径作弧,两弧相交于点P,作射线AP交BC于点D.若∠B=45°,∠C=2∠CAD,则∠BAE的度数为( )
A.15° B.25° C.30° D.35°
【解答】解:由题意可知,AP是EC的垂直平分线,
∴AD⊥BC,DE=CD,
∴△ADE≌△ADC(SAS),
∴∠EAD=∠CAD,∠C=∠AED,
∴∠EAC=2∠CAD,
∵∠C=2∠CAD,
∴∠C=∠EAC=∠AED,
∴△AEC是等边三角形,
∴∠C=∠EAC=∠AED=60°,
在△ABC中,∠B=45°,∠C=60°,
∴∠BAC=180°﹣45°﹣60°=75°,
∴∠BAE=75°﹣60°=15°.
故选:A.
6.(2分)如图,△ABC内接于⊙O,且OA⊥BC,若∠AOB=56°,则∠OAC的度数是( )
A.34° B.56° C.62° D.76°
【解答】解:如图,设OA⊥BC于D,
∵OA⊥BC,
∴∠ADC=90°,
∵∠AOB=56°,
∴∠C=AOB=28°,
∴∠OAC=180°﹣∠C﹣∠ADC=180°﹣28°﹣90°=62°,
故选:C.
二、填空题(每小题3分,共24分)
7.(3分)因式分解:2a2b+6ab2= 2ab(a+3b) .
【解答】解:2a2b+6ab2=2ab(a+3b).
故答案为:2ab(a+3b).
8.(3分)如图,松花江大桥的钢架结构采用三角形的形状,这其中运用的数学道理是 三角形的稳定性 .
【解答】解:松花江大桥的钢架结构采用三角形的形状,其中的数学道理是三角形的稳定性,
故答案为:三角形的稳定性.
9.(3分)如图,小雨把不等式3x+1>2(x﹣1)的解集表示在数轴上,则阴影部分盖住的数字是 ﹣3 .
【解答】解:去括号,得
3x+1>2x﹣2,
移项、合并同类项,得
x>﹣3,
故答案为:﹣3.
10.(3分)若关于x的一元二次方程3x2﹣3x+c=0没有实数根.则实数c的取值范围是 c> .
【解答】解:∵一元二次方程3x2﹣3x+c=0没有实数根,
∴Δ=(﹣3)2﹣4×3×c<0,
∴c>.
故答案为:c>.
11.(3分)如图,将直尺与含30°角的三角尺叠放在一起.若∠1=63°,则∠2的大小是 57° .
【解答】解:如图,
由题意得∠ABC=60°,
∵∠1=63°,
∴∠CBD=180°﹣∠1﹣∠ABC=57°,
由直尺可得:AC∥BD,
∴∠2=∠CBD=57°.
故答案为:57°.
12.(3分)一个三层折叠花架如图所示,已知AB∥CD∥EF,AC=30cm,CE=50cm,BD=45cm,则BF的长为 120 cm.
【解答】解:∵AB∥CD∥EF,
∴=,
∵AC=30cm,CE=50cm,BD=45cm,
∴=,
解得:DF=75,
则BF=BD+DF=45+75=120(cm),
故答案为:120.
13.(3分)《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间,设规定时间为x天,则可列出正确的方程为 .
【解答】解:由题意可得:
,
故答案为:.
14.(3分)如图所示,在矩形ABCD中,如图AB<BC,以点C为圆心,CB的长为半径的圆分别交AD边于点E,交CD边的延长线于点F.若AE=DF,的长为π,则DE的长为 2 .
【解答】解:连接CE,则CB=CE=CF,
设CB=R,
∵四边形ABCD是矩形,
∴CE=CF=DA,
∵AE=DF,
∴DE=DC,
∴DCE=45°,
∵的长为π,
∴=π,
解得R=4,
在Rt△DCE中,
DE=CE sin 45°=4×B=2.
故答案为:2.
三、解答题(每小题5分,共20分)
15.(5分)计算:(﹣1+3)×2+4÷(﹣2)﹣20240.
【解答】解:(﹣1+3)×2+4÷(﹣2)﹣20240
=2×2+4÷(﹣2)﹣1
=4+(﹣2)+(﹣1)
=1.
16.(5分)已知:如图,在 ABCD中,点E,F分别在AD,BC上,且BE平分∠ABC.若DE=CF,连结EF.求证:四边形ABFE是菱形.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵DE=CF,
∴AE=BF,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
17.(5分)2024年2月,第十四届全国冬季运动会在内蒙古自治区举办,吉祥物蒙古彩娃“安达”和“赛努”深受人民喜爱.某商店在销售一种印有蒙古彩娃的文化衫时,按文化衫每件标价的8折销售15件的销售额,与按文化衫每件的标价降低10元销售16件的销售额相等,求文化衫每件的标价.
【解答】解:设文化衫每件的标价为x元,
根据题意得:15×0.8x=16(x﹣10),
解得:x=40.
答:文化衫每件的标价为40元.
18.(5分)《义务教育课程方案》和《义务教育劳动课程标准(2022年版)》正式发布,劳动课正式成为中小学一门独立课程.为培养同学们爱劳动的习惯,某校开展了“做好一件家务”主题活动,要求人人参与.9年1班评选出了近期做家务表现优秀的一男三女共四名同学,准备从这四名同学中随机选取两名同学分享体会,请用画树状图或列表的方法求所选同学中有男生的概率.
【解答】解:列表如下:
男 女 女 女
男 (男,女) (男,女) (男,女)
女 (女,男) (女,女) (女,女)
女 (女,男) (女,女) (女,女)
女 (女,男) (女,女) (女,女)
共有12种等可能的结果,其中所选同学中有男生的结果有6种,
∴所选同学中有男生的概率为=.
四、解答题(每小题7分,共28分)
19.(7分)如图,点P(3,2)在反比例函数的图象上,过点P作PM∥x轴交反比例函数的图象于点M,作PN∥y轴交反比例函数的图象于点N,连接MN.
(1)求k的值;
(2)求△PMN的面积.
【解答】解:(1)∵点P(3,2)在反比例函数的图象上,
∴k=2×3=6.
(2)设点P(m,),则M(,),N(m,)
∴S△PMN=
=×)
=×
=.
20.(7分)图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点.点A、B、E、H均在格点上.只用无刻度的直尺在给定的网格中,分别按下列要求画图,保留作图痕迹.
(1)在图①中,以AB为腰画一个等腰直角三角形ABC;
(2)在图②中,画△ABE的高线ED;
(3)在图③中,在AB边上找一点F,连接HF,使得HF平分△ABH的面积.
【解答】解:(1)如图①中,△ABC即为所求(答案不唯一);
(2)如图②中,线段ED即为所求;
(3)如图③中,线段HF即为所求.
21.(7分)木栏头灯塔是矗立在海南岛文晶市的一座航标灯塔(如图①),被称为“亚洲第一灯塔”,如图②,虎威岛A位于木栏头灯塔O的南偏西50°方向上,一艘轮船在B处测得灯塔O位于它的北偏西45°方向上,轮船沿着正北方向航行3km后,到达位于灯塔O正东方向上的C处,该船继续向北航行至直线AO上的点D处.
(1)填空:∠BOC= 45 度,∠D= 50 度;
(2)求点D到灯塔O的距离(参考数据sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,≈1.73.结果精确到小数点后一位).
【解答】解:(1)由题意可知,OC⊥BD,
∵∠CBO=45°,
∴∠BOC=90°﹣∠CBO=45°,
∴∠COD=180°﹣50°﹣90°=40°,
∴∠D=90°﹣∠COD=50°,
故答案为:45,50;
(2)由题意可知:BC=3km,
在Rt△BOC中,
∠CBO=45°,
∴OC=BC=3km,
在Rt△DOC中,∠D=50°,
∴OD==≈3.9(km),
答:点D到灯塔O的距离约为3.9km.
22.(7分)某校举办“跨学科综合实践活动”,五名评委对每组同学的参赛作品进行打分.对参加比赛的甲、乙、丙三个组参赛作品得分(单位:分)的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、丙两组参赛作品得分的折线图:
b.在给乙组参赛作品的打分中,其中三位评委打分分别为87,93,95,其余两位评委的打分均高于85;
c.甲、乙、丙三个组参赛作品得分的平均数:
甲组 乙组 丙组
88 90 n
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)若某组参赛作品评委打分的5个数据的方差越小,则认为评委对该组参赛作品的评价越“一致”.据此推断:对于甲、丙两组的参赛作品,五位评委评价更“一致”的是 丙 组(填“甲”或“丙”);
(3)该校现准备推荐一个小组的作品到区里参加比赛,你认为应该推荐哪个小组,请说明理由.
【解答】解:(1)由题意得,n==90;
(2)由折线统计图可知,丙组数据的波动比甲组的小,所以五位评委评价更“一致”的是丙组.
故答案为:丙;
(3)由题意可知,乙组和丙组的平均数均为90分,比甲组的平均数88分高,所以从乙组和丙组推荐一个小组的作品到区里参加比赛,
又因为乙组的最低分比丙组的最低分高,所以应该推荐乙组.
五、解答题(每小题8分,共16分)
23.(8分)蓄电池发展水平是制约新能源汽车发展的关键要素.小明爸爸根据自家电动汽车仪表显示,感觉蓄电池充满电后,用前半部分电量所行驶的路程,总要比用后半部分电量行驶的路程更远一些.于是小明细心观察了充满电后汽车的行驶情况,并将蓄电池剩余电量y(千瓦时)和已行驶路程x(千米)的相关数据,用函数图象表示如下.
(1)电池充满电时的电量为 60 千瓦时;
(2)求BC所对应的函数关系式(不要求写出自变量的取值范围);
(3)在电量允许的情况下,如果在某段连续行驶时间里,汽车消耗了10千瓦时的电量,直接写出这段时间连续行驶路程s的取值范围.
【解答】解:(1)观察函数图象可知,电池充满电的电量为60千瓦时;
故答案为:60;
(2)设BC所对应的函数关系式为 y=kx+b,
把(150,35)和(200,10)代入得:
,
解得,
∴BC所对应的函数关系式为y=﹣x+110;
(3)当在AB段消耗了10千瓦时的电量时,s=×10=60(千米);
当在BC段消耗了10千瓦时的电量时,s=×10=20(千米);
∴20≤s≤60.
24.(8分)综合与探究
问题情境:数学课上,同学们以直角三角形纸片为背景进行探究性活动.如图1,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C逆时针旋转,使线段AB的对应线段A'B'恰好经过点B,得到图2,线段A'C与AB相交于点D.
初步分析:(1)判断△CBB'的形状,并说明理由;
深入探究:(2)乐学组的同学将图2中的△BDC沿射线BA的方向平移得到△EFG(点E,F,G分别是点B,D,C的对应点),线段EG,FG分别与边AC相交于点M,N.
①如图3,当点M恰好是线段EG的中点时,他们发现MN=FN,请证明这个结论;
②若BC=4,当点N恰好是线段AM的中点时,请直接写出△BDC平移的距离.
【解答】(1)解:△CBB′是等边三角形,理由如下:
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
由旋转得:BC=B′C,∠B′=∠ABC=60°,
∴△CBB′是等边三角形;
(2)①证明:如图3,连接EN,
∵△CBB′是等边三角形,
∴∠BCB′=60°,
由旋转得:∠A′CB′=∠ACB=90°,
∴∠BCD=∠ACB﹣∠BCB′
=90°﹣60°
=30°,
∴∠BDC=180°﹣∠BCD﹣∠CBD=90°,
由平移得:∠G=∠BCD=30°,∠EFG=∠BDC=90°,EG∥BC,
∴EF=EG,∠EMN=∠ACB=90°,
∵点M恰好是线段EG的中点,
∴EM=EG,
∴EF=EM,
在Rt△EFN和Rt△EMN中,
,
∴Rt△EFN≌Rt△EMN(HL),
∴MN=FN;
②解:设MN=x,
∵N是AM的中点,
∴AN=x,AM=2x,
由①得:GN=2MN=2x,AE=2EM,AB=2BC=8,
∴MG==x,
∵EM2+AM2=AE2,
∴EM2+(2x)2=(2EM)2,
解得:EM=x,
∴EG=EM+MG=x+x=x,
由平移得:EG=BC=4,
解得:x=.
∴EM=×=,
∴AE=2EM=,
∴BE=AB﹣AE=8﹣=,
故△BDC平移的距离为.
六、解答题(每小题10分,共20分)
25.(10分)如图,在△ABC中,∠ACB=90°,BC=2,AC=4,CD是边AB上的中线,动点P从点C出发,以每秒个单位长度的速度沿线段CD向终点D运动.过点P作PQ⊥AC于点Q,以PQ为边作等腰直角三角形PQN,∠QPN=90°,使点N、C始终在PQ的两侧.设点P的运动时间为t(s)(t>0),△PQN与△ADC重合部分图形的面积为S.
(1)用含t的代数式表示DP的长;
(2)当点N落在边AB上时,求t的值;
(3)求S关于t的函数关系式,并写出自变量t的取值范围.
【解答】解:(1)∵∠ACB=90°,BC=2,AC=4,
∴AB===2,
∵CD是边AB的中线,
∴DC=AB=,
∵动点P从点C出发,以每秒个单位长度的速度沿折线CD﹣DB向终点B运动,
∴PC=t,
∴DP=﹣t,
(2)当点N落在AB边上时,点P只能在CD上,
∵CD是直角三角形ABC的中线,则△ACD为等腰三角形,
则∠DCA=∠A=α,
则tanA==tanα,则sinα=,cosα=,
过点D作DH⊥NP于点H,
由题意得,△NPD为等腰三角形,且∠DNP=∠A=α,
则NP=2HP=2PDcosα=2×(﹣t)×=4﹣4t,
而PQ=PCsinα=t ,
∴t=4﹣4t,
解得:t=;
(3)当0<t时,由(2)知PQ=t,
∴△PQN与△ADC重合部分图形的面积S=;
当<t<1时,如图,过点H作HF⊥PN于点F,
由(2)知PE=4﹣4t,
∴EN=PN﹣PE=5t﹣4,
∵tanA=tan∠FEH=,
∴,
∴,即,
∴HF=,
∴=,
∴△PQN与△ADC重合部分图形的面积S=S△PQN﹣S△ENH==﹣,
即.
26.(10分)如图,在平面直角坐标系中,抛物线y=x2+ax﹣3(a为常数)经过点(﹣1,0).
(1)求此抛物线对应的函数解析式;
(2)点P在此抛物线上,其横坐标为m.
①当点P在y轴右侧,且点P到x轴的距离等于3,求点P的坐标;
②若点Q也在此抛物线上,其横坐标为m+1,当点P、Q之间(含点P、Q)的抛物线上恰好只有一个点到x轴的距离等于5时,请直接写出m的取值范围;
(3)设点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),连接EF,当抛物线y=x2+ax﹣3(a为常数)和线段EF只有一个公共点时,直接写出n的取值范围.
【解答】解:(1)由题意,把点(﹣1,0)代入抛物线 y=x2+ax﹣3,
∴0=12﹣a﹣3.
∴a=﹣2.
∴抛物线的函数解析式为y=x2﹣2x﹣3.
(2)①由题意,设点P的坐标为(m,3),
∵P到x轴的距离等于3,即|y|=3,
∴y=3或y=﹣3.
当y=3时,3=m2﹣2m﹣3,
∴ 或 .
当y=﹣3时.﹣3=m2﹣2m﹣3,
∴m=0或m=2.
∵P点在y轴右侧,
∴m>0.
∴ 或m=2.
∴P ,3)或 (2,﹣3).
②∵P、Q之间只有一个点到x轴的距离为5,
∴y1=5,即5=m2﹣2m﹣3.
∴m=﹣2或m=4.
∵点Q的横坐标为m+1,且点P、Q之间(含P、Q)的抛物线上恰好只有一个点到x轴的距离等于5,
∴﹣3≤m≤﹣2或3≤m≤4.
(3))∵点E的坐标为(n﹣2,n﹣2),
∴yE=n﹣2,xE=n﹣2,即yE=xE,
∴点E在直线y=x上,
∵点F的坐标为(n+2,n﹣2),
∴同理可求出点F在直线y=x﹣4上,
结合平移可知:直线y=x向右平移4个单位即可得到直线y=x﹣4,
设直线y=x、y=x﹣4与抛物线y=x2﹣2x﹣3交于点A、B、C、D四点,
∵点E的坐标为(n﹣2,n﹣2),点F的坐标为(n+2,n﹣2),
∴EF=n+2﹣(n﹣2)=4,且线段EF在直线y=n﹣2上,
∴DF∥x轴,
如图,
联立:,
解得:,.
∴,.
联立:.
解得:,.
∴,.
结合图形可知:当点E在点A与点B之间(含点A,不含点B)或者当点F在点C与点D之间(含点D,不含点C)时,抛物线y=x2﹣2x﹣3和线段EF只有一个有公共点,
∴<n﹣2≤或<n+2≤.
∴<n≤或<n≤.
第1页(共1页)
同课章节目录
