4.14.2垂线(一)课件(北京课改版七年级上)
文档属性
| 名称 | 4.14.2垂线(一)课件(北京课改版七年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 18.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-19 00:00:00 | ||
图片预览



文档简介
课件21张PPT。4.14 相交线、平行线
垂线(一)教学内容?
?? 1. 理解垂线的意义和垂线的第 一个性质。
2.会用三角板过一点画已知 直线的垂线。重点:垂线的意义、性质和画法;
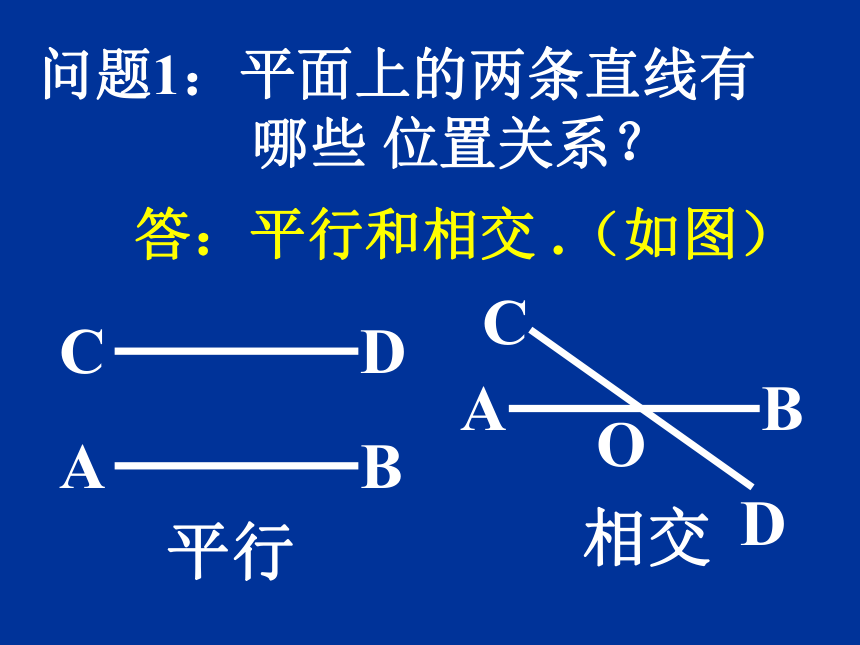
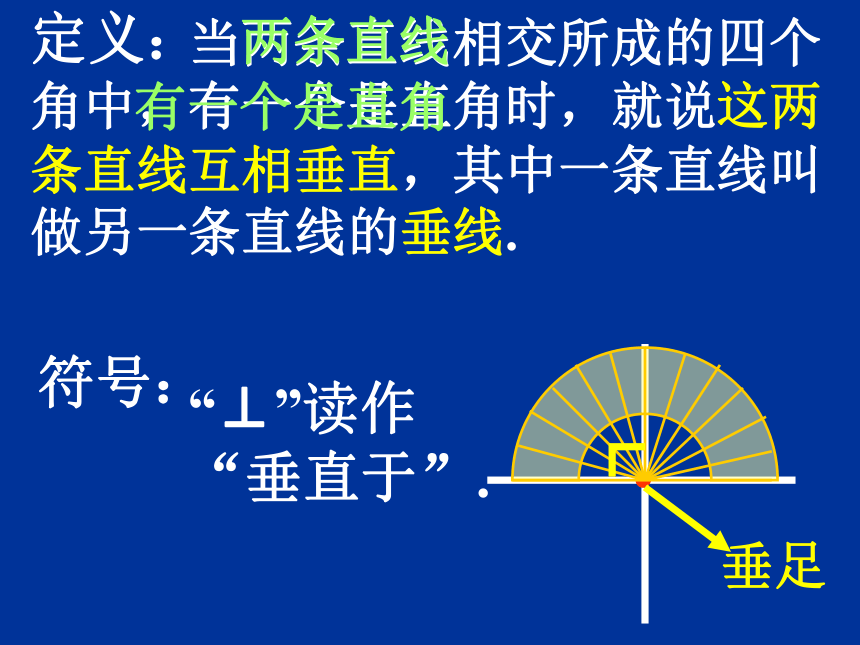
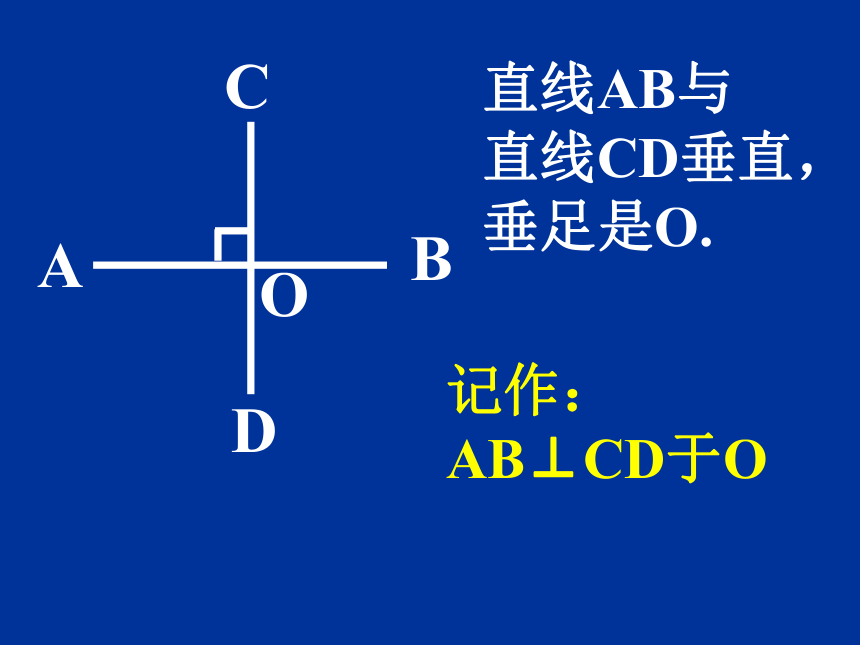
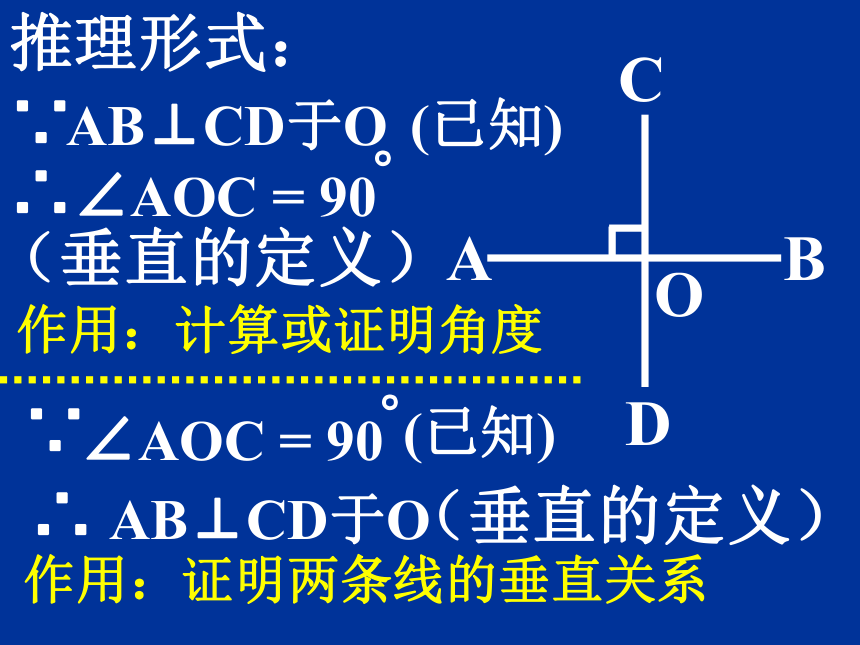
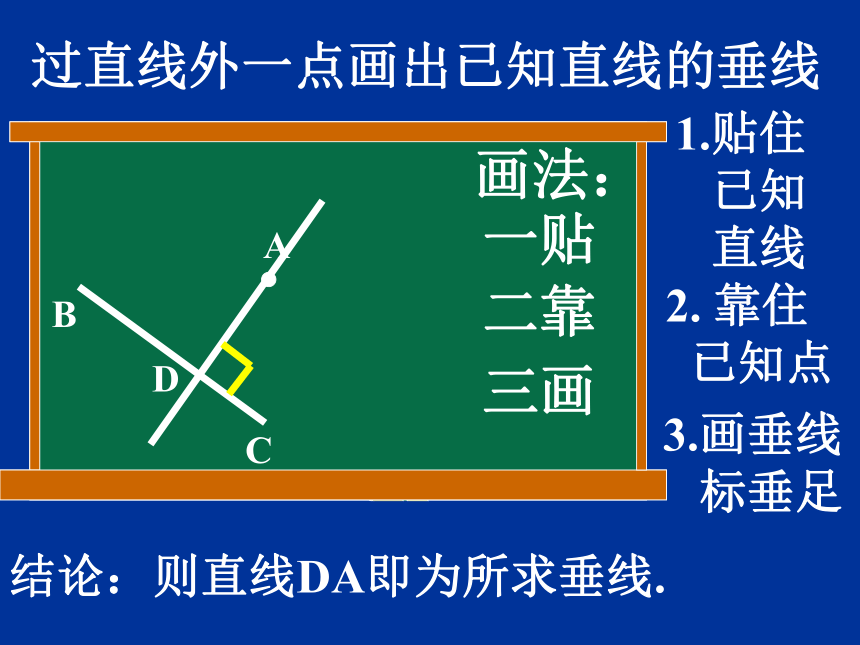
难点:垂线的画法 。平行相交O问题1:平面上的两条直线有 哪些 位置关系?答:平行和相交 .(如图)问题2:两条直线所夹的角中,如果 按照角的大小来分类,又有 哪几种? 当两条直线相交所成的四个角中,有一个是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线. “⊥”读作 “垂直于”. 定义:符号:有一个是直角两条直线记作:AB⊥CD于O 直线AB与 直线CD垂直, 垂足是O. ABCDOAB⊥CD于O ∵∴(已知)(垂直的定义)∵(已知)AB⊥CD于O ∴(垂直的定义)推理形式:作用:计算或证明角度作用:证明两条线的垂直关系CO过直线外一点画出已知直线的垂线 D一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线DA即为所求垂线.过直线上一点画出已知直线的垂线 一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线m即为所求垂线.m练习:在图中,过点A分别作BD和DE的垂线.NM结论:直线AM,AN为所求垂线.垂线的性质:
过一点有且只有一条直线
与已知直线垂直.注:与直线公理对比过两点有且只有一条直线注:①“有”指“存在”,“只有”指“唯一”。②“过一点”的点在直线外,或在 直线上都可以。结论:
直线FM,FN
为所求垂线。应用举例:例1. 画∠AOB=120°,画∠AOB 的平分线OE, 在OE上取一点F, 过F做OA,OB的垂线.例2.如图,已知AB与EF相交于O, ∠AOE= 30°,AB⊥CD于O.求∠EOD的度数.
∵AB⊥CD于O ∴ ∠COA= 90° 又 ∠AOC+∠AOD=180。 ∴ ∠AOD= 90。 又 ∠AOE= 30。 ∴ ∠EOD = 60。D解:例3.O如图,AO⊥BO于O, 求∠AOD和∠BOC的和.练习:按要求画图:ABCABCABC过B点作的AC垂线; 过A点作的BC垂线; 过C点作的AB垂线.结论:略小结:1.理解垂线的意义.2.根据垂线的意义,过一点 画一条直线的垂线.
3.理解垂线的第一条性质.作业:
1.整理笔记
2.补充练习(1)画∠AOB = 45。,在∠AOB 内找一点F, 过F点作OA,OB 的垂线 。(2)如图,直线AB⊥CD于O,过O点的直线EF平分∠AOD,
求∠COE的大小。
(3)如图,AB⊥EF于O, CD⊥AB于Q,
指出∠AQD与∠AOF的关系。
垂线(一)教学内容?
?? 1. 理解垂线的意义和垂线的第 一个性质。
2.会用三角板过一点画已知 直线的垂线。重点:垂线的意义、性质和画法;
难点:垂线的画法 。平行相交O问题1:平面上的两条直线有 哪些 位置关系?答:平行和相交 .(如图)问题2:两条直线所夹的角中,如果 按照角的大小来分类,又有 哪几种? 当两条直线相交所成的四个角中,有一个是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线. “⊥”读作 “垂直于”. 定义:符号:有一个是直角两条直线记作:AB⊥CD于O 直线AB与 直线CD垂直, 垂足是O. ABCDOAB⊥CD于O ∵∴(已知)(垂直的定义)∵(已知)AB⊥CD于O ∴(垂直的定义)推理形式:作用:计算或证明角度作用:证明两条线的垂直关系CO过直线外一点画出已知直线的垂线 D一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线DA即为所求垂线.过直线上一点画出已知直线的垂线 一贴二靠1.贴住 已知 直线 2. 靠住 已知点画法: 3.画垂线 标垂足三画结论:则直线m即为所求垂线.m练习:在图中,过点A分别作BD和DE的垂线.NM结论:直线AM,AN为所求垂线.垂线的性质:
过一点有且只有一条直线
与已知直线垂直.注:与直线公理对比过两点有且只有一条直线注:①“有”指“存在”,“只有”指“唯一”。②“过一点”的点在直线外,或在 直线上都可以。结论:
直线FM,FN
为所求垂线。应用举例:例1. 画∠AOB=120°,画∠AOB 的平分线OE, 在OE上取一点F, 过F做OA,OB的垂线.例2.如图,已知AB与EF相交于O, ∠AOE= 30°,AB⊥CD于O.求∠EOD的度数.
∵AB⊥CD于O ∴ ∠COA= 90° 又 ∠AOC+∠AOD=180。 ∴ ∠AOD= 90。 又 ∠AOE= 30。 ∴ ∠EOD = 60。D解:例3.O如图,AO⊥BO于O, 求∠AOD和∠BOC的和.练习:按要求画图:ABCABCABC过B点作的AC垂线; 过A点作的BC垂线; 过C点作的AB垂线.结论:略小结:1.理解垂线的意义.2.根据垂线的意义,过一点 画一条直线的垂线.
3.理解垂线的第一条性质.作业:
1.整理笔记
2.补充练习(1)画∠AOB = 45。,在∠AOB 内找一点F, 过F点作OA,OB 的垂线 。(2)如图,直线AB⊥CD于O,过O点的直线EF平分∠AOD,
求∠COE的大小。
(3)如图,AB⊥EF于O, CD⊥AB于Q,
指出∠AQD与∠AOF的关系。
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
