4.14.2垂线的性质课件(北京课改版七年级上)
文档属性
| 名称 | 4.14.2垂线的性质课件(北京课改版七年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 944.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-19 19:59:00 | ||
图片预览






文档简介
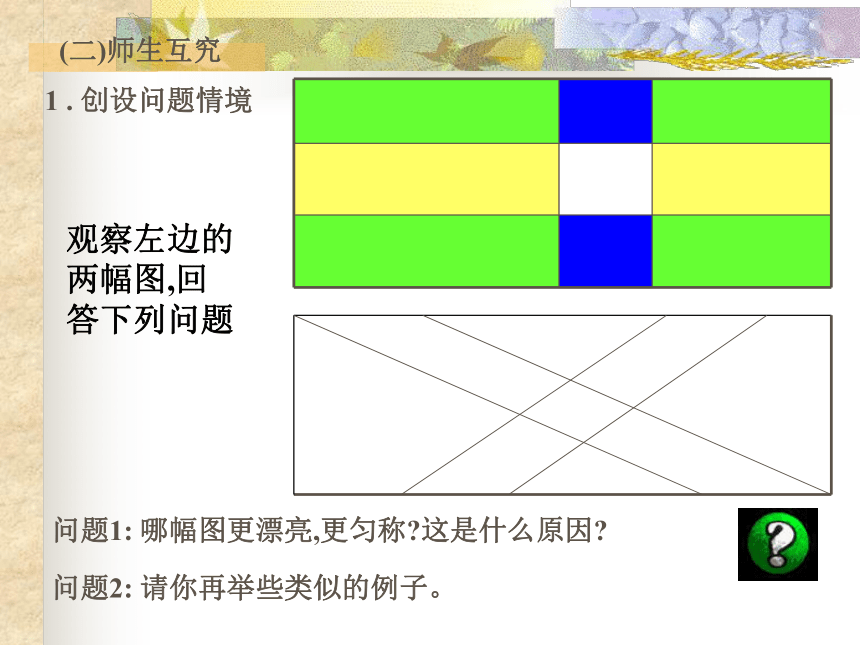
课件18张PPT。欢 迎 光 临敬 请 指 导!探究垂线的相关性质 (一)背景(二)师生互究问题1: 哪幅图更漂亮,更匀称?这是什么原因? 问题2: 请你再举些类似的例子。1 . 创设问题情境观察左边的
两幅图,回
答下列问题2.提 高
问题1:两直线相交,有两组分别相等的角,当一个角等于90°时,其他三个角发生怎样的变化?可能产生四个相等的角吗?问题2:AB与CD交于点O如果将直线CD绕着点O旋转,∠BOD=90°时,
∠AOC,∠AOD ,∠ BOC的度数是多少?问题:你们的依据是什么?两直线互相垂直:两条直线相交所构成的四个角中有一个是直角时,称这两条直线互相垂直。3 .提升ABCDO∟
例如:直线AB与CD相交,交点O,∠BOC=90° ,
记为:2)若已知直线AB⊥CD,垂足为点O,则读作:AB垂直于CD,或
AB与CD互相垂直(perpendicular) AB ⊥CD,点O为垂足(foot of a
perpendicular).∠AOC=∠AOD=∠BOC=∠BOD=90°再探究: 请同学们再举一些日常生活中垂直的例子?问题:请同学们用三角尺或量角器作为工具
1)在图中经过直线AB外一点P,与直线外AB垂直,
且讨论这样的垂线有几条?
2)若点P在直线AB上,情况又会怎样?PABAPB归纳得出:
1)靠已知直线----找待过定点------画已知直线的垂线
(一靠二过三垂直) .
2)在平面有一条并且只有一条,没有第二条.
问题:互相交流画图过程和“有且只有”的含义.归纳:在同一平面内,经过直线外(或上)一点
有且只有一条直线与已知直线垂直。问题:
如图:请同学们相互比试,谁能更快地过直线CD上一点P作
直线AB的垂线,并在小组间进行交流.
CDPAB∟O探索:
如图所示:点A到直线CD上各点的距离长短一样吗?谁最短?他具备什么条件?归纳: 连接直线外一点与直线上各点的所有线段中,
垂线段最短。提高:线段AB的长度就是点A到直线CD的距离.. ACBD∟不一样,(AB < AC < AD)
线段AB最短,AB⊥DC .
简单说成:
垂线段最短。思考:点A到直线DC的距离与点A到点C的距离有什么区别?点A到直线DC的距离:
线段AB的长度,A为直线外一点,B为过A点向直线 DC所引的垂线的垂足.
点A到点C的距离:两点之间线段的长度.1. 如图,∠ABD=90°
1)点B在直线____上,
点D在直线____外;
2)直线____与直线____相交与点A,
点D是直线 ____与直线____的交点,
也是直线____与直线____的交点,
又是直线____与直线____的交点;
3)直线___ ⊥直线____,垂足为点___;
4)过点D有且只有____条直线与直线AC垂直.(三)较量AB
CD∟ACACABADADBDADCDBDCDBDACB一2.如图所示的各个三角形中,分别画出AB边上的高.BCAABCBCA∟∟∟DD3 .应用
某村在如图所示的河边,为解决村庄供水问题,需把河中水
引到村庄A处,在河岸CD的什么地方开沟,
才能使沟最短?画出图来,并说明道理.小
河CD.
村庄∟(四).探索与思考:
1 .学校的位置如图所示,请在图上设计出学校到两条公路的
最短路线,并说明理由.
.
学校 ADCB∟∟ 2 .在空间,是否有三条不同的直线a,b,c,满足a⊥b,b ⊥c,
c ⊥a同时成立?在空间,过直线上一点与该直线垂直的
直线有几条?过空间一点与 已知平面垂直的直线有几条?成立;无数条;一条。 谢 谢 !
两幅图,回
答下列问题2.提 高
问题1:两直线相交,有两组分别相等的角,当一个角等于90°时,其他三个角发生怎样的变化?可能产生四个相等的角吗?问题2:AB与CD交于点O如果将直线CD绕着点O旋转,∠BOD=90°时,
∠AOC,∠AOD ,∠ BOC的度数是多少?问题:你们的依据是什么?两直线互相垂直:两条直线相交所构成的四个角中有一个是直角时,称这两条直线互相垂直。3 .提升ABCDO∟
例如:直线AB与CD相交,交点O,∠BOC=90° ,
记为:2)若已知直线AB⊥CD,垂足为点O,则读作:AB垂直于CD,或
AB与CD互相垂直(perpendicular) AB ⊥CD,点O为垂足(foot of a
perpendicular).∠AOC=∠AOD=∠BOC=∠BOD=90°再探究: 请同学们再举一些日常生活中垂直的例子?问题:请同学们用三角尺或量角器作为工具
1)在图中经过直线AB外一点P,与直线外AB垂直,
且讨论这样的垂线有几条?
2)若点P在直线AB上,情况又会怎样?PABAPB归纳得出:
1)靠已知直线----找待过定点------画已知直线的垂线
(一靠二过三垂直) .
2)在平面有一条并且只有一条,没有第二条.
问题:互相交流画图过程和“有且只有”的含义.归纳:在同一平面内,经过直线外(或上)一点
有且只有一条直线与已知直线垂直。问题:
如图:请同学们相互比试,谁能更快地过直线CD上一点P作
直线AB的垂线,并在小组间进行交流.
CDPAB∟O探索:
如图所示:点A到直线CD上各点的距离长短一样吗?谁最短?他具备什么条件?归纳: 连接直线外一点与直线上各点的所有线段中,
垂线段最短。提高:线段AB的长度就是点A到直线CD的距离.. ACBD∟不一样,(AB < AC < AD)
线段AB最短,AB⊥DC .
简单说成:
垂线段最短。思考:点A到直线DC的距离与点A到点C的距离有什么区别?点A到直线DC的距离:
线段AB的长度,A为直线外一点,B为过A点向直线 DC所引的垂线的垂足.
点A到点C的距离:两点之间线段的长度.1. 如图,∠ABD=90°
1)点B在直线____上,
点D在直线____外;
2)直线____与直线____相交与点A,
点D是直线 ____与直线____的交点,
也是直线____与直线____的交点,
又是直线____与直线____的交点;
3)直线___ ⊥直线____,垂足为点___;
4)过点D有且只有____条直线与直线AC垂直.(三)较量AB
CD∟ACACABADADBDADCDBDCDBDACB一2.如图所示的各个三角形中,分别画出AB边上的高.BCAABCBCA∟∟∟DD3 .应用
某村在如图所示的河边,为解决村庄供水问题,需把河中水
引到村庄A处,在河岸CD的什么地方开沟,
才能使沟最短?画出图来,并说明道理.小
河CD.
村庄∟(四).探索与思考:
1 .学校的位置如图所示,请在图上设计出学校到两条公路的
最短路线,并说明理由.
.
学校 ADCB∟∟ 2 .在空间,是否有三条不同的直线a,b,c,满足a⊥b,b ⊥c,
c ⊥a同时成立?在空间,过直线上一点与该直线垂直的
直线有几条?过空间一点与 已知平面垂直的直线有几条?成立;无数条;一条。 谢 谢 !
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
