高一下册期末测试培优卷(含解析)
文档属性
| 名称 | 高一下册期末测试培优卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 06:58:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
高一下册期末测试培优卷(含解析)
一、选择题
1.已知向量 , 满足 ,且 ,则 的取值范围是( )
A. B. C. D.
2.若 ( 是虚数单位),则 的最小值是( )
A. B. C. D.
3. 过多面体上三点作多面体的截面时作图的理由是( )
A.如果不同的两个平面,有一个公共点,那么,的交集是过点的直线
B.如果直线有两个点在平面内,那么直线在平面内
C.不在同一直线上的三点确定一个平面
D.以上理由皆正确
4. 设是的外心,点为的中点,满足,若,则面积的最大值为( )
A.2 B.4 C. D.8
5.在某次美术专业测试中,若甲 乙 丙三人获得优秀等级的概率分别是和0.5,且三人的测试结果相互独立,则测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率为( )
A. B. C. D.
6.校足球社团为学校足球比赛设计了一个奖杯,如图,奖杯的设计思路是将侧棱长为的正三棱锥的三个侧面沿,,展开得到面,,,使得平面,,均与平面垂直,再将球放到上面使得,,三个点在球的表面上,若奖杯的总高度为,且,则球的表面积为( )
A. B. C. D.
7.已知函数在有且仅有两个零点,且,则图象的一条对称轴是( )
A. B. C. D.
8.如图,在棱长为1的正方体中,点分别在线段和上.给出下列四个结论中所有正确结论的个数有( )个
①的最小值为1②四面体的体积为③存在无数条直线与垂直④点为所在边中点时,四面体的外接球半径为
A.1 B.2 C.3 D.4
二、多项选择题
9.下列说法正确的是( )
A.残差图中若样本数据对应的点分布的带状区域越狭窄,说明该模型的拟合精度越高
B.在频率分布直方图中,各小长方形的面积等于各组的频数
C.数据1,3,4,5,7,9,11,16的第75百分位数为9
D.某校共有男女学生1500人,现按性别采用分层抽样的方法抽取容量为100人的样本,若样本中男生有55人,则该校女生人数是675人
10.在正四面体ABCD中,若为BC的中点,下列结论正确的是( )
A.正四面体外接球的表面积为
B.正四面体的体积为
C.如果点在线段DM上,则的最小值为
D.正四面体ABCD内接一个圆柱,使圆柱下底面在底面BCD上,上底圆面与面ABD、面ABC、面ACD均只有一个公共点,则圆柱的侧面积的最大值为
11.如图,棱长为2的正方体中,为棱的中点,为正方形内一个动点(包括边界),且平面,则下列说法正确的有( )
A.记的中点为,上存在一点,使得面面
B.动点轨迹的长度为
C.三棱锥体积的最小值为
D.当三棱锥的体积最大时,其外接球的表面积为
三、填空题
12.已知向量与的夹角为,且,,若与的夹角为锐角,则的取值范围是 .
13.有一种投掷骰子走跳棋的游戏:棋盘上标有第1站、第2站、第3站、…、第10站,共10站,设棋子跳到第n站的概率为,若一枚棋子开始在第1站,棋手每次投掷骰子一次,棋子向前跳动一次.若骰子点数小于等于3,棋子向前跳一站;否则,棋子向前跳两站,直到棋子跳到第9站(失败)或者第10站(获胜)时,游戏结束.则 ;该棋手获胜的概率为 .
14.在直四棱柱中,所有棱长均为2,,为的中点,点在四边形内(包括边界)运动,下列结论中正确的是 (填序号)
①当点在线段上运动时,四面体的体积为定值
②若,则的最小值为
③若的外心为M,则为定值2
④若,则点的轨迹长度为
四、解答题
15.在锐角中,角A,B,C所对应的边分别为a,b,c,已知.
(1)求角B的值;
(2)若,求的周长的取值范围.
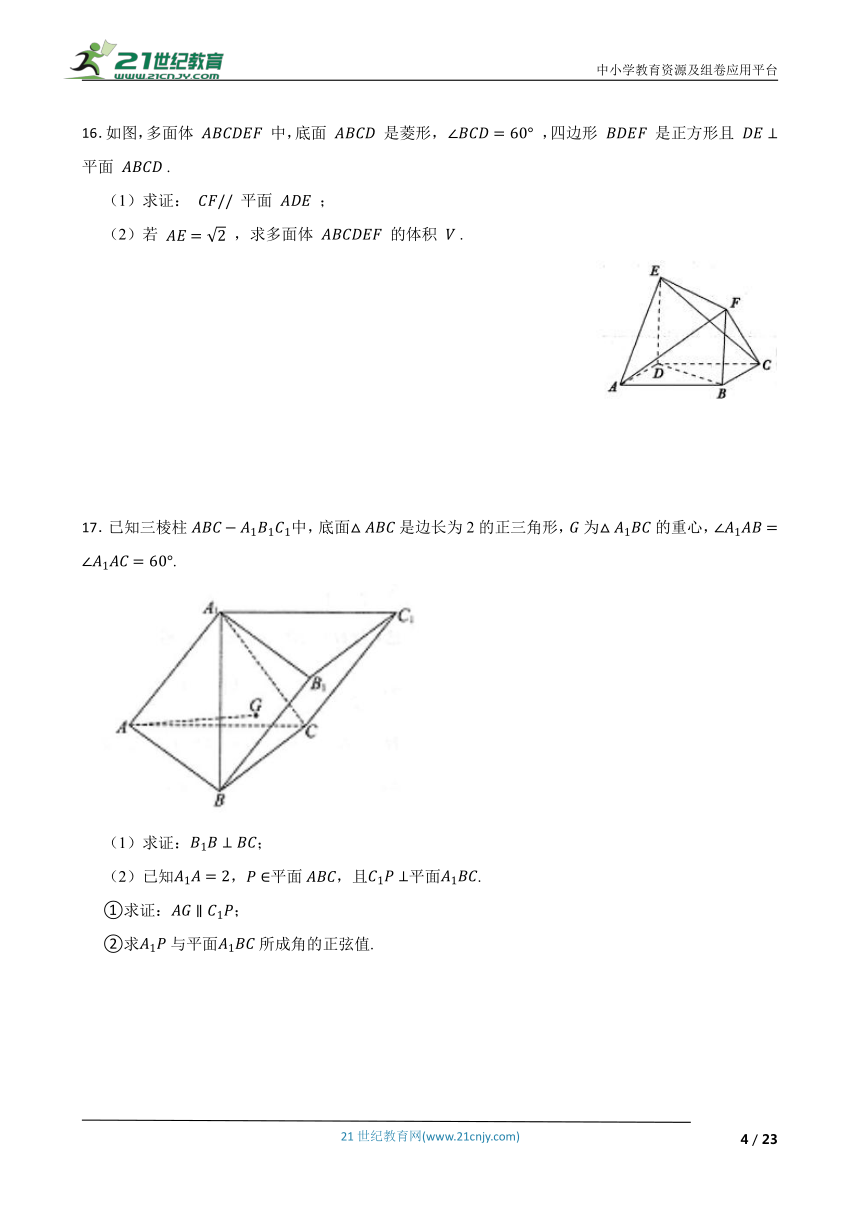
16.如图,多面体 中,底面 是菱形, ,四边形 是正方形且 平面 .
(1)求证: 平面 ;
(2)若 ,求多面体 的体积 .
17.已知三棱柱中,底面是边长为2的正三角形,为的重心,.
(1)求证:;
(2)已知,平面,且平面.
①求证:;
②求与平面所成角的正弦值.
18.为普及消防安全知识,某学校组织相关知识竞赛.比赛共分为两轮,每位参赛选手均须参加两轮比赛,若其在两轮比赛中均胜出,则视为赢得比赛.已知在第一轮比赛中,选手甲、乙胜出的概率分别为,;在第二轮比赛中,甲、乙胜出的概率分别为,,甲、乙两人在每轮比赛中是否胜出互不影响.
(1)甲在比赛中恰好赢一轮的概率;
(2)从甲、乙两人中选1人参加比赛,派谁参赛赢得比赛的概率更大?
(3)若甲、乙两人均参加比赛,求两人中至少有一人赢得比赛的概率.
19.如图(1),在中,,,、、分别为边、、的中点,以为折痕把折起,使点到达点位置(如图(2)).
(1)当时,求二面角的大小;
(2)当四棱锥的体积最大时,分别求下列问题:
①设平面与平面的交线为,求证:平面;
②在棱上是否存在点,使得与平面所成角的正弦值为?若存在,求的长;若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】由 可得 即 ,
设向量 , 夹角为 ,则 ,
由数量积的定义可得: ,
因为 ,所以 ,
所以 ,
当 时,显然成立;
当 时,可得 ,
因为 ,所以 ,因为 ,
所以 ,即 ,可得 ,
所以 ,
所以 的取值范围是: 。
故答案为:B.
【分析】利用已知条件结合数量积求向量的模的公式,再结合数量积的定义,从而求出 ,再利用分类讨论的方法结合数量积求向量的夹角公式,从而结合一元二次不等式求解集的方法,进而求出 的取值范围 。
2.【答案】D
【解析】【解答】解:由复数的几何意义可知: 表示的点在单位圆上,
而|z 2 2i|表示该单位圆上的点到复数 表示的点 的距离,
由图象可知: 的最小值应为点 到 的距离,
而 ,圆的半径为1,
故 的最小值为 ,
故答案为:D.
【分析】易得复数 表示的点在单位圆上,而要求的值为单位圆上的点到复数 表示的点 的距离,由数形结合的思想可得答案.
3.【答案】D
【解析】【解答】A、因为不同的两个平面,有一个公共点, 根据公理3可知 ,的交集是过点的直线 ,故选项A正确;
B、 直线有两个点在平面内, 根据公理1可知 直线在平面内 ,故选项B正确;
C、根据公理2可知选项C正确;
故选:D.
【分析】本题主要考查学生对空间中点、直线、平面之间的位置关系的四个公理的记忆和理解:
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内(对应选项B).
公理2:过不在一条直线上的三点,有且只有一个平面(对应选项C).
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)(对应选项A).
公理4:(平行线的传递性)平行与同一直线的两条直线互相平行.
4.【答案】B
【解析】【解答】解:已知如图所示:
因为,,
所以,
从而,即,
所以,所以,
所以的面积为
,
等号成立当且仅当,
综上所述,面积的最大值为4.
故选:B.
【分析】利用平面向量的数量积公式,再结合余弦定理可化简为:,再利用三角形面积公式、同角三角函数关系进行化简可得,利用二次函数的性质可求出面积的最大值.
5.【答案】A
【解析】【解答】解:设甲、乙、丙三人获得优秀等级分别为事件A,B,C,三人中恰有两人没达优秀等级为事件D,
因为则
,
,
所以测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率.
故答案为:A.
【分析】利用已知条件结合对立事件、互斥事件求概率公式得出的值,再结合条件概型求概率公式得出测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率.
6.【答案】C
【解析】【解答】解:连接、、,取、、中点、、,连接、、如图所示:
由题意可知:,且,
则,
因为平面,,均与平面垂直,
设,,三点所在的圆为圆,底面的中心为,则,
又因为奖杯总高度为,
设球半径为,球心到圆面的距离为,
则,即,
因为≌,,
所以是边长为的等边三角形,
设的外接圆半径为,则,在直角中,,即,解得,
所以球的表面积为.
故答案为:C.
【分析】作辅助线,设球半径为,球心到圆面的距离为,可知,的外接圆半径为,结合球的性质可得,即可得球的表面积.
7.【答案】C
【解析】【解答】解:因为函数在有且仅有两个零点,设其周期为T,
则,且解得当时,令,
又因为所以,解得,由①②可得:,
因为
所以的图像的一条对称轴是由由③④可得:,;
综上可得函数图像的对称轴为,则当时,.
故答案为:C.
【分析】本题主要考查三角函数的周期及对称轴等性质,根据 函数在有且仅有两个零点 ,可得,然后再根据,求得再进行综合即可求得答案.
8.【答案】B
【解析】【解答】解:点M、N在线段和线段上,且由题意知直线和直线为异面直线,
当MN为直线和直线的公垂线线段时最短.
由正方体的性质知:平面又平面,则
同理可得:,即是直线和直线的公垂线,故MN的最小值为=1,
则①正确;由正方体的性质知:,则当点M在上运动时,点M到平面NBC的
距离不变,距离d=1,又由知,点N在直线运动时,N到直线的的距离不变,
所以三角形NBC的面积不变,则,故 ② 错误;连结
,由正方体的性质知平面,且又平面,则又
,, 平面,则平面,当N不在线段端点时,过
N作交于E,过N作交于F,平面NEF交线段于M,
平面,平面,平面,同理可得:平面,
又,且平面NEF,所以平面NEF平面,故平面NEF,
又平面NEF,则,又点N在线段上,所以存在无数条直线,故 ③ 正确;
如图:以点D位原点,以DA为x轴,DC为y轴,为z轴建立空间直角坐标系
则M(),,,
则,则,有正玄定理得的外接圆半径
因为N为的中点,所以可证得为等腰三角形,的外接圆圆心,设四面体NMBC的外接球
球心为O,则平面NBC,故可设,由OM=OC=OB,可得:
解得:,所以四面体NMBC的外接球的半径为:,故 ④ 错误.
故答案为:B.
【分析】对于A选项可以根据异面直线之间公垂线段最短进行判定,对于B选项线面平行的性质知道:当点M在上运动时,点M到平面NBC的距离不变,然后再结合三棱锥的体积公式进行求解即可,对于C选项根据线面垂直的判定以及面面平行的性质即可判定,对于D选项利用空间直角坐标系简化运算,再在和正弦定理和勾股定理可求出四面体NMBC的外接球的半径.
9.【答案】A,D
【解析】【解答】对于A,由残差定义,如果样本数据点分布的带状区域越狭窄,说明该模型的拟合精度越高,故A正确;
对于B,在频率分布直方图中,各小长方形的面积等于相应各组的频率,故B错误;
对于C,因为,故该组数据的第75百分位数为第6个数和第7个数的平均数10,故C错误;
对于D,设该校女生人数为n,由已知可得,解得n=675,故D正确.
故选:AD.
【分析】 根据残差的定义即可判断A;根据频率分布直方图的特征即可判断B;根据百分位数的定义即可判断C;根据分层抽样的抽样比即可求解判断D.
10.【答案】A,C,D
【解析】【解答】解:由正四面体各棱都相等,即各面都为正三角形,故棱长为2,如下图示:
为底面中心,则共线,为体高,故,
所以,故正四面体的体积为,
由题设,外接球球心在上,且半径,
所以,则,
故外接球的表面积为,A正确;B错误;
由题意知:将面与面沿翻折,使它们在同一个平面,如下图示:
所以且,,
又,而,
要使最小,只需共线,则,
所以,C正确;
如下图所示:
棱锥中一个平行于底面的截面所成正三角形的内切圆为正四面体内接一个圆柱的上底面,
若截面所成正三角形边长为,则圆柱体的高,圆柱底面半径为,
所以其侧面积,故当时,,D正确.
故选:ACD
【分析】由正四棱锥的结构特征,应用棱锥的体积公式求体积,并确定外接球的半径求表面积,展开侧面,要使最小,只需共线,结合余弦定理求其最小值,根据正四面体内接一个圆柱底面圆与其中截面正三角形关系求半径、体高,应用二次函数性质求侧面积最大值.
11.【答案】A,C,D
【解析】【解答】解:选项A:当点P为的中点时,利用面面平行的判定即可证明出面面;A正确;
选项B:取中点,中点,连接,
又为棱的中点,所以,
根据线面平行的判定可得平面,平面,
又,面,所以面平面,
又平面,面,所以面,
又为正方形内的一个动点(包括边界),所以面面,
又面面,所以,即动点轨迹为,
又,所以选项B错误;
选项C:易知面,所以三棱锥体积为,
所以面积最小值时,体积最小,
如图,由选项A知,,易知在处时,面积最小,
此时,
所以三棱锥体积的最小值为,故选项C正确;
对于选项D,如图,当三棱锥体积最大时,在处,
如图建立空间直角坐标系如图所示:
设球心为,外接球的半径为,
易知,
所以①,②,
③,④,
联立①②③④解得,,所以,故外接球的表面积为,所以选项D正确,
故答案为:ACD.
【分析】由面,利用正方体特征找到平面平面,进而得到动点轨迹为,从而可判断出选项A和B的正误;根据棱锥的体积公式,得到面积最小值时,体积最小,即可求出三棱锥体积的最小值,从而判断出选项C的正误;选项D,建立空间直角坐标系,直接求出外接球径,即可求出结果.
12.【答案】
【解析】【解答】因为向量与的夹角为,且,,与的夹角为锐角,
所以,且与不共线,
由,得,
所以,
化简得,
解得或,
由与共线,得存在唯一实数,使,
所以,得,
所以当时,与不共线,
综上所述,或,且,
所以的取值范围是。
故答案为:。
【分析】利用向量与的夹角为,且,,与的夹角为锐角,再利用数量积定义得出,且与不共线,再利用数量积的运算法则得出实数的取值范围,由与共线结合向量共线定理得出当时,与不共线,从而求出实数的取值范围。
13.【答案】;
【解析】【解答】由题,因为,故,由,所以,累加可得:.
故答案为:;.
【分析】首先由已知条件结合概率的加法以及乘法公式计算出结果,再由题意结合等比数列的前n项和公式,代入数值计算出结果即可。
14.【答案】①④
15.【答案】(1),由正弦定理得:,
即,
由余弦定理得:,
因为,
所以;
(2)锐角中,,,
由正弦定理得:,
故,
则
,
因为锐角中,,
则,,
解得:,
故,,
则,
故,
所以三角形周长的取值范围是.
16.【答案】(1)证明: 是菱形, .
又 平面 , 平面 , 平面 .又 是正方形, .
平面 , 平面 , 平面 . 平面 , 平面
平面 平面 , 平面
(2)解:连接 ,记 .
是菱形, ,且 .
由 平面 , 平面 , .
平面 , 平面 , ,
平面 于 ,
即 为四棱锥 的高.
由 是菱形, ,则 为等边三角形,由 ,则
, , , ,
【解析】【分析】(1)由面面平行的判定定理先证明平面 平面 ,进而可得 平面 ;(2)将多面体 拆成两个四棱锥,由四棱锥的体积公式即可求出结果.
17.【答案】(1)证明:连交于,连.
由于为的重心,所以为的中点.
在三棱柱中,因为,,,所以,从而.
由于为的中点,所以,,又,
所以平面,因为平面,所以,
因为,所以.
(2)证明:①∵,,∴为正三角形;同理,也为正三角形,∴,从而三棱锥的所有棱长均为2,该四面体为正四面体,
由于为的重心,∴平面,又平面,所以.
解:②设的重心为,,且,在平面内,过作,连,则平面.
以为原点,以,,分别为,,轴建立空间直角坐标系.
,
所以,,,,
,
所以.
设,与平面所成的角为,
则,
所以,
因为平面,所以设,由①知:,从而存在实数,使,
所以,解得:,,,
从而.,令,
,令,
.
【解析】【分析】(1)连交于,连接,由于为的重心,所以为的中点,再利用两三角形全等判断方法,进而证出,再结合两三角形全等的性质得出,再利用中点结合等腰三角形三线合一得出线线垂直,再由线线垂直证出线面垂直,从而由线面垂直的定义和线线平行证出.
(2)①利用已知条件结合正三角形的定义判断出三角形和三角形为正三角形,得到四面体为正四面体,结合为的重心,进而得出线面垂直,再结合直线平面证出.
②以为原点,以,,分别为,,轴建立空间直角坐标系,利用已知得出点P的坐标,再由向量共线的坐标表示得出向量坐标,再利用数量积求出与平面所成角的正弦值.
18.【答案】(1)解:设“甲在第一轮比赛中胜出”,“甲在第二轮比赛中胜出”,
“乙在第一轮比赛中胜出”,“乙在第二轮比赛中胜出”,
则,,,相互独立,且,,,,
设“甲在比赛中恰好赢一轮”
则
(2)解:因为在两轮比赛中均胜出赢得比赛,则“甲赢得比赛”,“乙赢得比赛”,
所以,
,
因为,所以派甲参赛获胜的概率更大
(3)解:设“甲赢得比赛”,“乙赢得比赛”,
于是“两人中至少有一人赢得比赛”,
由(2)知,,
所以,
,
所以
【解析】【分析】(1)根据概率的加法运算以及独立事件的乘法公式计算即可;
(2)分别求出甲乙赢的概率,再比较大小即可得出结论;
(3)再根据对立事件的概率公式,先求出两人都没有赢得比赛,从而可得出结论.
19.【答案】(1)解:翻折前,在中,,即,
、分别为、的中点,则且,
翻折后,在图(2)中,,,则二面角的平面角为,
因为,,由余弦定理可得,
,故,
即当时,二面角的大小为
(2)解:①过点在平面内作,垂足为点,
,,,则平面,
平面,,
,,平面,则,
故当平面时,四棱锥的体积取最大值,
,,,平面,
因为,,为的中点,所以,且,
故四边形为平行四边形,所以,,
平面,平面,平面,
因为平面,平面平面,,因此,平面;
②因为平面,与平面所成角为,
因为平面,,
所以,,解得,
在中,,,,
由余弦定理可得,
所以,,解得或.
因此,在棱上存在点,使得与平面所成角的正弦值为,且或.
【解析】【分析】(1)利用已知条件结合翻折的方法,再结合二面角的平面角的作图方法,进而找出二面角的平面角为 ,再利用余弦定理以及三角形中角的取值范围,进而得出的值,从而得出二面角的大小 。
(2) ①过点在平面内作,垂足为点,再利用线线垂直证出线面垂直,再结合线面垂直证出线线垂直,所以,再利用结合线线垂直证出线面垂直,所以平面,则,故当平面时,四棱锥的体积取最大值,再利用线线垂直证出线面垂直,再结合中点作中位线的方法和中位线的性质以及平行的传递性,所以且,故四边形为平行四边形,所以,再利用线线平行证出线面平行,从而证出平面,再利用线面平行的性质定理证出线线平行,所以,因此,平面。
②利用平面,所以与平面所成角为,再利用线面垂直的定义证出线线垂直,所以,再利用正弦函数的定义得出EN的长,在中,,,,由余弦定理可得PN的长,因此,在棱上存在点,使得与平面所成角的正弦值为,且或。
21世纪教育网(www.21cnjy.com)
高一下册期末测试培优卷(含解析)
一、选择题
1.已知向量 , 满足 ,且 ,则 的取值范围是( )
A. B. C. D.
2.若 ( 是虚数单位),则 的最小值是( )
A. B. C. D.
3. 过多面体上三点作多面体的截面时作图的理由是( )
A.如果不同的两个平面,有一个公共点,那么,的交集是过点的直线
B.如果直线有两个点在平面内,那么直线在平面内
C.不在同一直线上的三点确定一个平面
D.以上理由皆正确
4. 设是的外心,点为的中点,满足,若,则面积的最大值为( )
A.2 B.4 C. D.8
5.在某次美术专业测试中,若甲 乙 丙三人获得优秀等级的概率分别是和0.5,且三人的测试结果相互独立,则测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率为( )
A. B. C. D.
6.校足球社团为学校足球比赛设计了一个奖杯,如图,奖杯的设计思路是将侧棱长为的正三棱锥的三个侧面沿,,展开得到面,,,使得平面,,均与平面垂直,再将球放到上面使得,,三个点在球的表面上,若奖杯的总高度为,且,则球的表面积为( )
A. B. C. D.
7.已知函数在有且仅有两个零点,且,则图象的一条对称轴是( )
A. B. C. D.
8.如图,在棱长为1的正方体中,点分别在线段和上.给出下列四个结论中所有正确结论的个数有( )个
①的最小值为1②四面体的体积为③存在无数条直线与垂直④点为所在边中点时,四面体的外接球半径为
A.1 B.2 C.3 D.4
二、多项选择题
9.下列说法正确的是( )
A.残差图中若样本数据对应的点分布的带状区域越狭窄,说明该模型的拟合精度越高
B.在频率分布直方图中,各小长方形的面积等于各组的频数
C.数据1,3,4,5,7,9,11,16的第75百分位数为9
D.某校共有男女学生1500人,现按性别采用分层抽样的方法抽取容量为100人的样本,若样本中男生有55人,则该校女生人数是675人
10.在正四面体ABCD中,若为BC的中点,下列结论正确的是( )
A.正四面体外接球的表面积为
B.正四面体的体积为
C.如果点在线段DM上,则的最小值为
D.正四面体ABCD内接一个圆柱,使圆柱下底面在底面BCD上,上底圆面与面ABD、面ABC、面ACD均只有一个公共点,则圆柱的侧面积的最大值为
11.如图,棱长为2的正方体中,为棱的中点,为正方形内一个动点(包括边界),且平面,则下列说法正确的有( )
A.记的中点为,上存在一点,使得面面
B.动点轨迹的长度为
C.三棱锥体积的最小值为
D.当三棱锥的体积最大时,其外接球的表面积为
三、填空题
12.已知向量与的夹角为,且,,若与的夹角为锐角,则的取值范围是 .
13.有一种投掷骰子走跳棋的游戏:棋盘上标有第1站、第2站、第3站、…、第10站,共10站,设棋子跳到第n站的概率为,若一枚棋子开始在第1站,棋手每次投掷骰子一次,棋子向前跳动一次.若骰子点数小于等于3,棋子向前跳一站;否则,棋子向前跳两站,直到棋子跳到第9站(失败)或者第10站(获胜)时,游戏结束.则 ;该棋手获胜的概率为 .
14.在直四棱柱中,所有棱长均为2,,为的中点,点在四边形内(包括边界)运动,下列结论中正确的是 (填序号)
①当点在线段上运动时,四面体的体积为定值
②若,则的最小值为
③若的外心为M,则为定值2
④若,则点的轨迹长度为
四、解答题
15.在锐角中,角A,B,C所对应的边分别为a,b,c,已知.
(1)求角B的值;
(2)若,求的周长的取值范围.
16.如图,多面体 中,底面 是菱形, ,四边形 是正方形且 平面 .
(1)求证: 平面 ;
(2)若 ,求多面体 的体积 .
17.已知三棱柱中,底面是边长为2的正三角形,为的重心,.
(1)求证:;
(2)已知,平面,且平面.
①求证:;
②求与平面所成角的正弦值.
18.为普及消防安全知识,某学校组织相关知识竞赛.比赛共分为两轮,每位参赛选手均须参加两轮比赛,若其在两轮比赛中均胜出,则视为赢得比赛.已知在第一轮比赛中,选手甲、乙胜出的概率分别为,;在第二轮比赛中,甲、乙胜出的概率分别为,,甲、乙两人在每轮比赛中是否胜出互不影响.
(1)甲在比赛中恰好赢一轮的概率;
(2)从甲、乙两人中选1人参加比赛,派谁参赛赢得比赛的概率更大?
(3)若甲、乙两人均参加比赛,求两人中至少有一人赢得比赛的概率.
19.如图(1),在中,,,、、分别为边、、的中点,以为折痕把折起,使点到达点位置(如图(2)).
(1)当时,求二面角的大小;
(2)当四棱锥的体积最大时,分别求下列问题:
①设平面与平面的交线为,求证:平面;
②在棱上是否存在点,使得与平面所成角的正弦值为?若存在,求的长;若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】由 可得 即 ,
设向量 , 夹角为 ,则 ,
由数量积的定义可得: ,
因为 ,所以 ,
所以 ,
当 时,显然成立;
当 时,可得 ,
因为 ,所以 ,因为 ,
所以 ,即 ,可得 ,
所以 ,
所以 的取值范围是: 。
故答案为:B.
【分析】利用已知条件结合数量积求向量的模的公式,再结合数量积的定义,从而求出 ,再利用分类讨论的方法结合数量积求向量的夹角公式,从而结合一元二次不等式求解集的方法,进而求出 的取值范围 。
2.【答案】D
【解析】【解答】解:由复数的几何意义可知: 表示的点在单位圆上,
而|z 2 2i|表示该单位圆上的点到复数 表示的点 的距离,
由图象可知: 的最小值应为点 到 的距离,
而 ,圆的半径为1,
故 的最小值为 ,
故答案为:D.
【分析】易得复数 表示的点在单位圆上,而要求的值为单位圆上的点到复数 表示的点 的距离,由数形结合的思想可得答案.
3.【答案】D
【解析】【解答】A、因为不同的两个平面,有一个公共点, 根据公理3可知 ,的交集是过点的直线 ,故选项A正确;
B、 直线有两个点在平面内, 根据公理1可知 直线在平面内 ,故选项B正确;
C、根据公理2可知选项C正确;
故选:D.
【分析】本题主要考查学生对空间中点、直线、平面之间的位置关系的四个公理的记忆和理解:
公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内(对应选项B).
公理2:过不在一条直线上的三点,有且只有一个平面(对应选项C).
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线)(对应选项A).
公理4:(平行线的传递性)平行与同一直线的两条直线互相平行.
4.【答案】B
【解析】【解答】解:已知如图所示:
因为,,
所以,
从而,即,
所以,所以,
所以的面积为
,
等号成立当且仅当,
综上所述,面积的最大值为4.
故选:B.
【分析】利用平面向量的数量积公式,再结合余弦定理可化简为:,再利用三角形面积公式、同角三角函数关系进行化简可得,利用二次函数的性质可求出面积的最大值.
5.【答案】A
【解析】【解答】解:设甲、乙、丙三人获得优秀等级分别为事件A,B,C,三人中恰有两人没达优秀等级为事件D,
因为则
,
,
所以测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率.
故答案为:A.
【分析】利用已知条件结合对立事件、互斥事件求概率公式得出的值,再结合条件概型求概率公式得出测试结束后,在甲 乙 丙三人中恰有两人没达优秀等级的前提条件下,乙没有达优秀等级的概率.
6.【答案】C
【解析】【解答】解:连接、、,取、、中点、、,连接、、如图所示:
由题意可知:,且,
则,
因为平面,,均与平面垂直,
设,,三点所在的圆为圆,底面的中心为,则,
又因为奖杯总高度为,
设球半径为,球心到圆面的距离为,
则,即,
因为≌,,
所以是边长为的等边三角形,
设的外接圆半径为,则,在直角中,,即,解得,
所以球的表面积为.
故答案为:C.
【分析】作辅助线,设球半径为,球心到圆面的距离为,可知,的外接圆半径为,结合球的性质可得,即可得球的表面积.
7.【答案】C
【解析】【解答】解:因为函数在有且仅有两个零点,设其周期为T,
则,且解得当时,令,
又因为所以,解得,由①②可得:,
因为
所以的图像的一条对称轴是由由③④可得:,;
综上可得函数图像的对称轴为,则当时,.
故答案为:C.
【分析】本题主要考查三角函数的周期及对称轴等性质,根据 函数在有且仅有两个零点 ,可得,然后再根据,求得再进行综合即可求得答案.
8.【答案】B
【解析】【解答】解:点M、N在线段和线段上,且由题意知直线和直线为异面直线,
当MN为直线和直线的公垂线线段时最短.
由正方体的性质知:平面又平面,则
同理可得:,即是直线和直线的公垂线,故MN的最小值为=1,
则①正确;由正方体的性质知:,则当点M在上运动时,点M到平面NBC的
距离不变,距离d=1,又由知,点N在直线运动时,N到直线的的距离不变,
所以三角形NBC的面积不变,则,故 ② 错误;连结
,由正方体的性质知平面,且又平面,则又
,, 平面,则平面,当N不在线段端点时,过
N作交于E,过N作交于F,平面NEF交线段于M,
平面,平面,平面,同理可得:平面,
又,且平面NEF,所以平面NEF平面,故平面NEF,
又平面NEF,则,又点N在线段上,所以存在无数条直线,故 ③ 正确;
如图:以点D位原点,以DA为x轴,DC为y轴,为z轴建立空间直角坐标系
则M(),,,
则,则,有正玄定理得的外接圆半径
因为N为的中点,所以可证得为等腰三角形,的外接圆圆心,设四面体NMBC的外接球
球心为O,则平面NBC,故可设,由OM=OC=OB,可得:
解得:,所以四面体NMBC的外接球的半径为:,故 ④ 错误.
故答案为:B.
【分析】对于A选项可以根据异面直线之间公垂线段最短进行判定,对于B选项线面平行的性质知道:当点M在上运动时,点M到平面NBC的距离不变,然后再结合三棱锥的体积公式进行求解即可,对于C选项根据线面垂直的判定以及面面平行的性质即可判定,对于D选项利用空间直角坐标系简化运算,再在和正弦定理和勾股定理可求出四面体NMBC的外接球的半径.
9.【答案】A,D
【解析】【解答】对于A,由残差定义,如果样本数据点分布的带状区域越狭窄,说明该模型的拟合精度越高,故A正确;
对于B,在频率分布直方图中,各小长方形的面积等于相应各组的频率,故B错误;
对于C,因为,故该组数据的第75百分位数为第6个数和第7个数的平均数10,故C错误;
对于D,设该校女生人数为n,由已知可得,解得n=675,故D正确.
故选:AD.
【分析】 根据残差的定义即可判断A;根据频率分布直方图的特征即可判断B;根据百分位数的定义即可判断C;根据分层抽样的抽样比即可求解判断D.
10.【答案】A,C,D
【解析】【解答】解:由正四面体各棱都相等,即各面都为正三角形,故棱长为2,如下图示:
为底面中心,则共线,为体高,故,
所以,故正四面体的体积为,
由题设,外接球球心在上,且半径,
所以,则,
故外接球的表面积为,A正确;B错误;
由题意知:将面与面沿翻折,使它们在同一个平面,如下图示:
所以且,,
又,而,
要使最小,只需共线,则,
所以,C正确;
如下图所示:
棱锥中一个平行于底面的截面所成正三角形的内切圆为正四面体内接一个圆柱的上底面,
若截面所成正三角形边长为,则圆柱体的高,圆柱底面半径为,
所以其侧面积,故当时,,D正确.
故选:ACD
【分析】由正四棱锥的结构特征,应用棱锥的体积公式求体积,并确定外接球的半径求表面积,展开侧面,要使最小,只需共线,结合余弦定理求其最小值,根据正四面体内接一个圆柱底面圆与其中截面正三角形关系求半径、体高,应用二次函数性质求侧面积最大值.
11.【答案】A,C,D
【解析】【解答】解:选项A:当点P为的中点时,利用面面平行的判定即可证明出面面;A正确;
选项B:取中点,中点,连接,
又为棱的中点,所以,
根据线面平行的判定可得平面,平面,
又,面,所以面平面,
又平面,面,所以面,
又为正方形内的一个动点(包括边界),所以面面,
又面面,所以,即动点轨迹为,
又,所以选项B错误;
选项C:易知面,所以三棱锥体积为,
所以面积最小值时,体积最小,
如图,由选项A知,,易知在处时,面积最小,
此时,
所以三棱锥体积的最小值为,故选项C正确;
对于选项D,如图,当三棱锥体积最大时,在处,
如图建立空间直角坐标系如图所示:
设球心为,外接球的半径为,
易知,
所以①,②,
③,④,
联立①②③④解得,,所以,故外接球的表面积为,所以选项D正确,
故答案为:ACD.
【分析】由面,利用正方体特征找到平面平面,进而得到动点轨迹为,从而可判断出选项A和B的正误;根据棱锥的体积公式,得到面积最小值时,体积最小,即可求出三棱锥体积的最小值,从而判断出选项C的正误;选项D,建立空间直角坐标系,直接求出外接球径,即可求出结果.
12.【答案】
【解析】【解答】因为向量与的夹角为,且,,与的夹角为锐角,
所以,且与不共线,
由,得,
所以,
化简得,
解得或,
由与共线,得存在唯一实数,使,
所以,得,
所以当时,与不共线,
综上所述,或,且,
所以的取值范围是。
故答案为:。
【分析】利用向量与的夹角为,且,,与的夹角为锐角,再利用数量积定义得出,且与不共线,再利用数量积的运算法则得出实数的取值范围,由与共线结合向量共线定理得出当时,与不共线,从而求出实数的取值范围。
13.【答案】;
【解析】【解答】由题,因为,故,由,所以,累加可得:.
故答案为:;.
【分析】首先由已知条件结合概率的加法以及乘法公式计算出结果,再由题意结合等比数列的前n项和公式,代入数值计算出结果即可。
14.【答案】①④
15.【答案】(1),由正弦定理得:,
即,
由余弦定理得:,
因为,
所以;
(2)锐角中,,,
由正弦定理得:,
故,
则
,
因为锐角中,,
则,,
解得:,
故,,
则,
故,
所以三角形周长的取值范围是.
16.【答案】(1)证明: 是菱形, .
又 平面 , 平面 , 平面 .又 是正方形, .
平面 , 平面 , 平面 . 平面 , 平面
平面 平面 , 平面
(2)解:连接 ,记 .
是菱形, ,且 .
由 平面 , 平面 , .
平面 , 平面 , ,
平面 于 ,
即 为四棱锥 的高.
由 是菱形, ,则 为等边三角形,由 ,则
, , , ,
【解析】【分析】(1)由面面平行的判定定理先证明平面 平面 ,进而可得 平面 ;(2)将多面体 拆成两个四棱锥,由四棱锥的体积公式即可求出结果.
17.【答案】(1)证明:连交于,连.
由于为的重心,所以为的中点.
在三棱柱中,因为,,,所以,从而.
由于为的中点,所以,,又,
所以平面,因为平面,所以,
因为,所以.
(2)证明:①∵,,∴为正三角形;同理,也为正三角形,∴,从而三棱锥的所有棱长均为2,该四面体为正四面体,
由于为的重心,∴平面,又平面,所以.
解:②设的重心为,,且,在平面内,过作,连,则平面.
以为原点,以,,分别为,,轴建立空间直角坐标系.
,
所以,,,,
,
所以.
设,与平面所成的角为,
则,
所以,
因为平面,所以设,由①知:,从而存在实数,使,
所以,解得:,,,
从而.,令,
,令,
.
【解析】【分析】(1)连交于,连接,由于为的重心,所以为的中点,再利用两三角形全等判断方法,进而证出,再结合两三角形全等的性质得出,再利用中点结合等腰三角形三线合一得出线线垂直,再由线线垂直证出线面垂直,从而由线面垂直的定义和线线平行证出.
(2)①利用已知条件结合正三角形的定义判断出三角形和三角形为正三角形,得到四面体为正四面体,结合为的重心,进而得出线面垂直,再结合直线平面证出.
②以为原点,以,,分别为,,轴建立空间直角坐标系,利用已知得出点P的坐标,再由向量共线的坐标表示得出向量坐标,再利用数量积求出与平面所成角的正弦值.
18.【答案】(1)解:设“甲在第一轮比赛中胜出”,“甲在第二轮比赛中胜出”,
“乙在第一轮比赛中胜出”,“乙在第二轮比赛中胜出”,
则,,,相互独立,且,,,,
设“甲在比赛中恰好赢一轮”
则
(2)解:因为在两轮比赛中均胜出赢得比赛,则“甲赢得比赛”,“乙赢得比赛”,
所以,
,
因为,所以派甲参赛获胜的概率更大
(3)解:设“甲赢得比赛”,“乙赢得比赛”,
于是“两人中至少有一人赢得比赛”,
由(2)知,,
所以,
,
所以
【解析】【分析】(1)根据概率的加法运算以及独立事件的乘法公式计算即可;
(2)分别求出甲乙赢的概率,再比较大小即可得出结论;
(3)再根据对立事件的概率公式,先求出两人都没有赢得比赛,从而可得出结论.
19.【答案】(1)解:翻折前,在中,,即,
、分别为、的中点,则且,
翻折后,在图(2)中,,,则二面角的平面角为,
因为,,由余弦定理可得,
,故,
即当时,二面角的大小为
(2)解:①过点在平面内作,垂足为点,
,,,则平面,
平面,,
,,平面,则,
故当平面时,四棱锥的体积取最大值,
,,,平面,
因为,,为的中点,所以,且,
故四边形为平行四边形,所以,,
平面,平面,平面,
因为平面,平面平面,,因此,平面;
②因为平面,与平面所成角为,
因为平面,,
所以,,解得,
在中,,,,
由余弦定理可得,
所以,,解得或.
因此,在棱上存在点,使得与平面所成角的正弦值为,且或.
【解析】【分析】(1)利用已知条件结合翻折的方法,再结合二面角的平面角的作图方法,进而找出二面角的平面角为 ,再利用余弦定理以及三角形中角的取值范围,进而得出的值,从而得出二面角的大小 。
(2) ①过点在平面内作,垂足为点,再利用线线垂直证出线面垂直,再结合线面垂直证出线线垂直,所以,再利用结合线线垂直证出线面垂直,所以平面,则,故当平面时,四棱锥的体积取最大值,再利用线线垂直证出线面垂直,再结合中点作中位线的方法和中位线的性质以及平行的传递性,所以且,故四边形为平行四边形,所以,再利用线线平行证出线面平行,从而证出平面,再利用线面平行的性质定理证出线线平行,所以,因此,平面。
②利用平面,所以与平面所成角为,再利用线面垂直的定义证出线线垂直,所以,再利用正弦函数的定义得出EN的长,在中,,,,由余弦定理可得PN的长,因此,在棱上存在点,使得与平面所成角的正弦值为,且或。
21世纪教育网(www.21cnjy.com)
同课章节目录
