人教版八年级数学下册17.1勾股定理(1) 课件(共39张PPT)
文档属性
| 名称 | 人教版八年级数学下册17.1勾股定理(1) 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览



文档简介
(共39张PPT)
勾股定理(第一课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
思考:
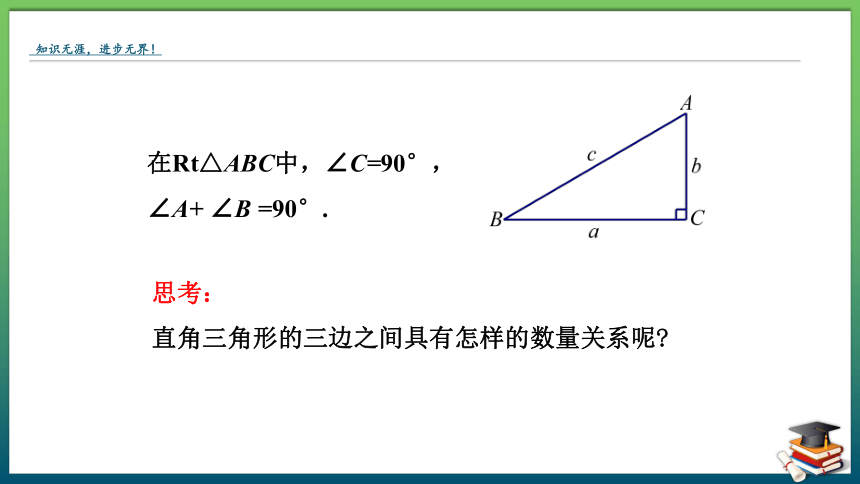
直角三角形的三边之间具有怎样的数量关系呢
在Rt△ABC中,∠C=90°,
∠A+ ∠B =90°.
探究一
我们也来观察一下地面的图案,你能发现三个正方形A,B ,C的面积之间有什么数量关系吗?
每块砖都是等腰直角三角形
请按下暂停键,1分钟后再继续学习。
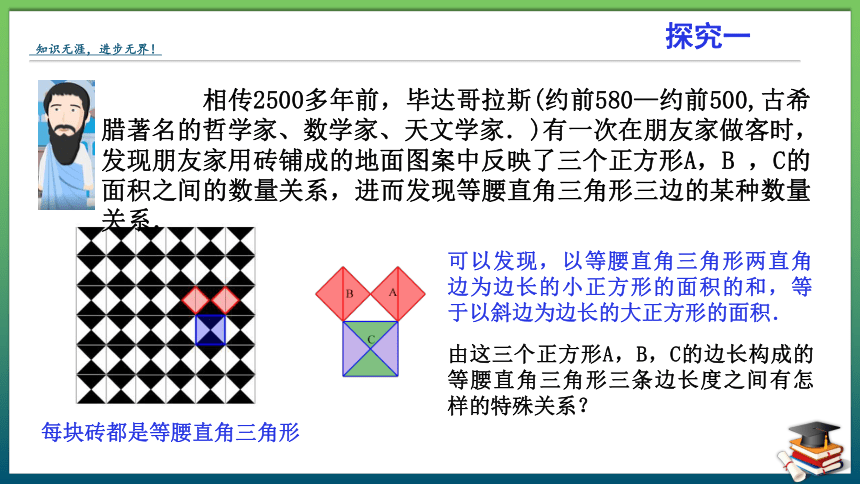
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
每块砖都是等腰直角三角形
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?
探究一
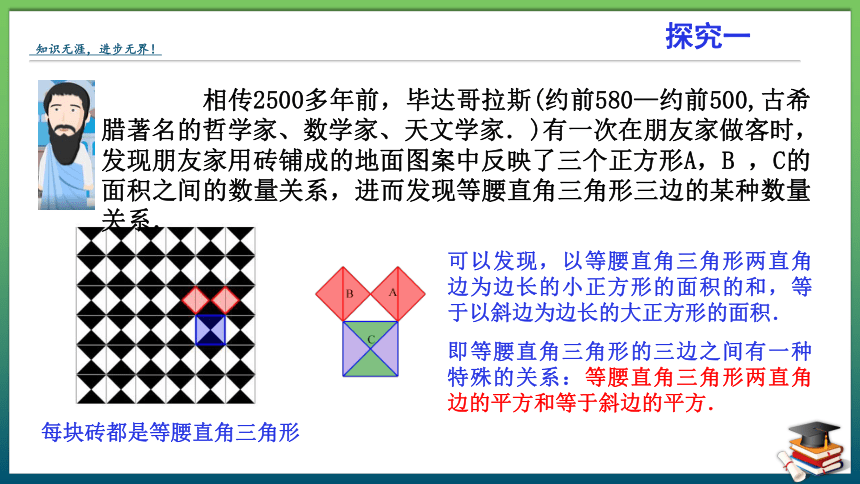
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
即等腰直角三角形的三边之间有一种特殊的关系:等腰直角三角形两直角边的平方和等于斜边的平方.
每块砖都是等腰直角三角形
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
探究一
A的面积 B的面积 C的面积
左图
右图
4
?
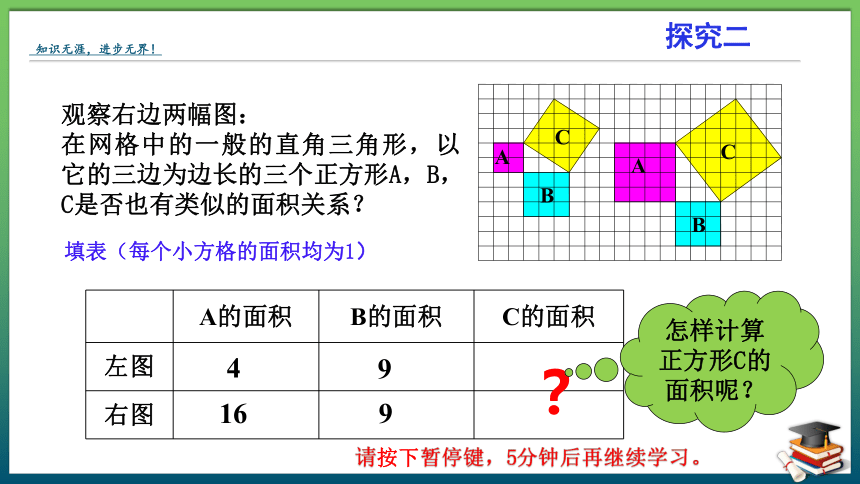
怎样计算正方形C的面积呢?
9
16
9
请按下暂停键,5分钟后再继续学习。
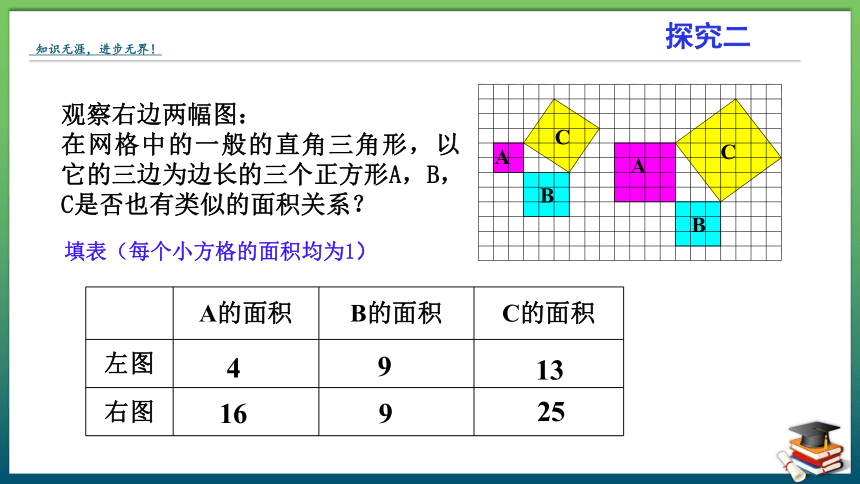
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A
B
C
C
B
A
探究二
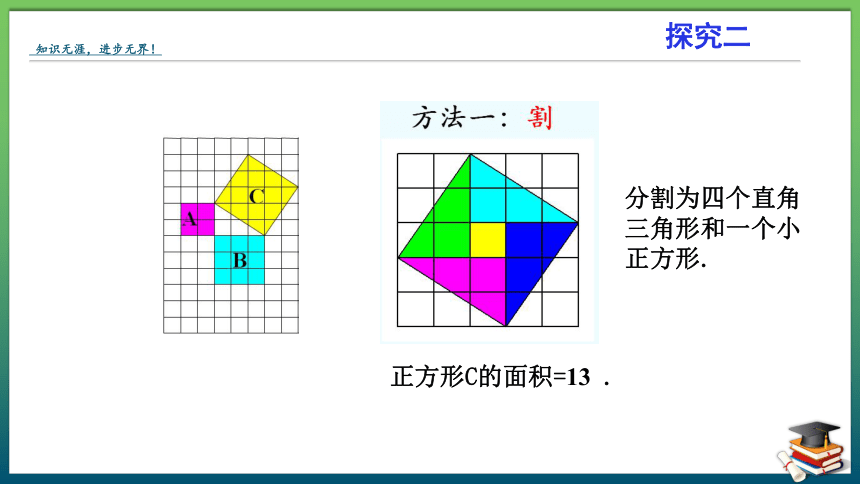
分割为四个直角三角形和一个小正方形.
正方形C的面积=13 .
探究二
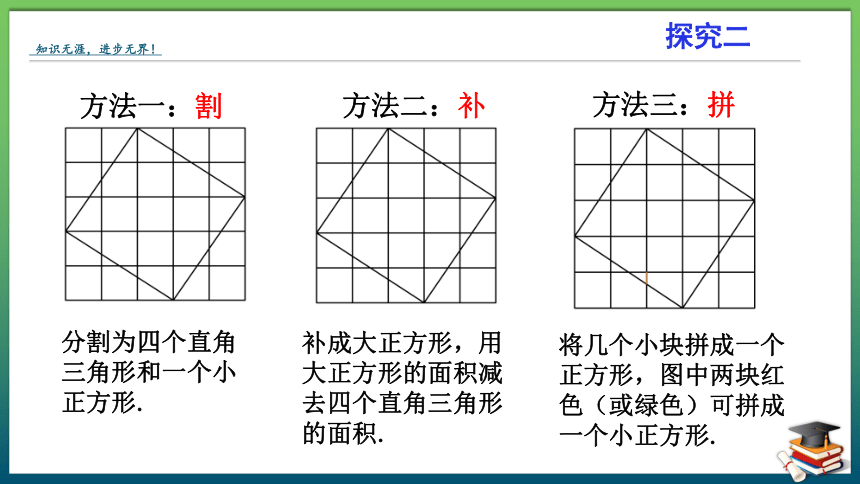
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成一个正方形,图中两块红色(或绿色)可拼成一个小正方形.
探究二
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A的面积 B的面积 C的面积
左图
右图
4
9
16
9
13
请按下暂停键,3分钟后再继续学习。
A
B
C
C
B
A
探究二
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A的面积 B的面积 C的面积
左图
右图
4
9
16
9
13
25
A
B
C
C
B
A
探究二
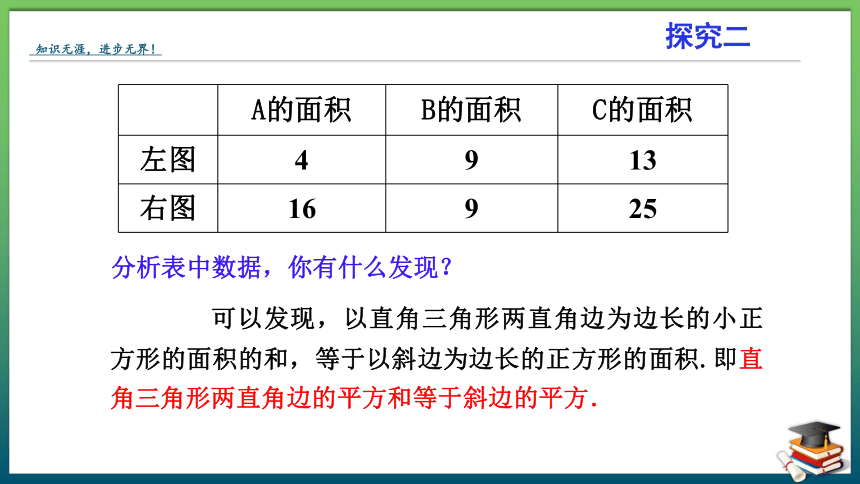
分析表中数据,你有什么发现?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
可以发现,以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.即直角三角形两直角边的平方和等于斜边的平方.
探究二
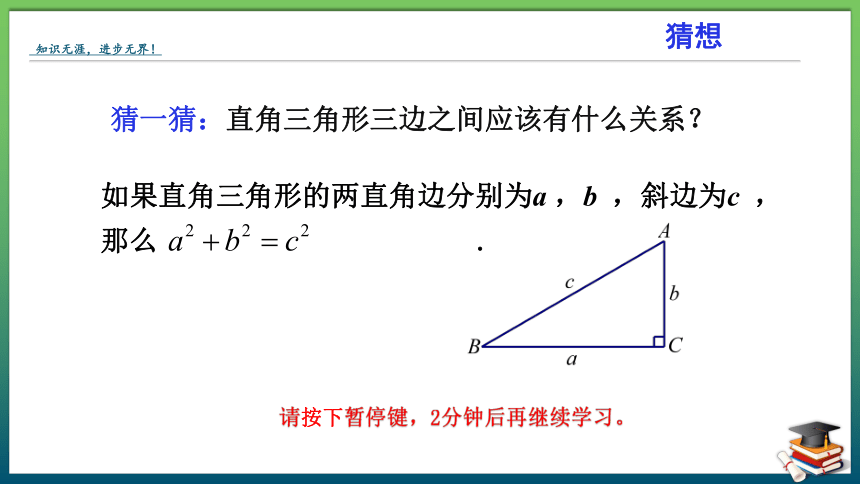
猜一猜:直角三角形三边之间应该有什么关系?
请按下暂停键,2分钟后再继续学习。
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
猜想
赵爽弦图证明法
b
a
赵爽拼图证明法:
以直角三角形的两条直角边a、b为边作两个正方形,
b
a
以直角三角形的两条直角边a,b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
赵爽拼图证明法:
c
b
a
图1
图2
赵爽弦图证明法
b
a
a
c
c
b
a
赵爽弦图证明法
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
“赵爽弦图”通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理.
勾股定理
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).
c
b
a
(
b
-
a
)
2
黄实
朱实
数学文化
勾股定理的证明方法很多,常见的是拼图的方法.
用拼图的方法验证勾股定理的思路是:
①图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.
勾股定理的证明方法
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
为啥命名为勾股定理呢?
勾股定理
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代把直角三角形中较短的直角边称为“勾” ,较长的直角边称为“股” ,斜边称为“弦” .
勾股定理和人类文明
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三,股四,弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.在我国勾股定理也叫做“商高定理” .
古希腊数学家毕达哥拉斯,在公元前5世纪给出了这个定理的证明,所以在国外这个定理也称为毕达哥拉斯定理,相传他证出这个定理后非常高兴,杀了一百头牛进行庆祝,于是也有人把它称为“百牛定理”.
勾股定理和人类文明
勾股定理的证明
1.传说中毕达哥拉斯的证法
请按下暂停键,2分钟后再继续学习。
1.传说中毕达哥拉斯的证法
勾股定理的证明
2.美国第20任总统加菲尔德的证法
勾股定理的证明
2.美国第20任总统加菲尔德的证法
试一试
请按下暂停键,2分钟后再继续学习。
勾股定理的证明
2.美国第20任总统加菲尔德的证法
化简得证:
,
,
.
勾股定理的证明
勾股定理在数学发展中起到了重大的作用,其证明方法据说有400多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
勾股定理的证明
练习1 求下列直角三角形中未知边的长度.
初步应用定理
(1)
(2)
请按下暂停键,2分钟后再继续学习。
练习1 求下列直角三角形中未知边的长度.
初步应用定理
(1)
(2)
答案: (1)8;(2)13.
练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
请按下暂停键,2分钟后再继续学习。
初步应用定理
练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
答案: 625.
初步应用定理
通过这种方法,可以把一个正方形的面积分成若干个小正方形的面积的和,不断地分下去,就可以得到一棵美丽的勾股树.
初步应用定理
课堂小结
1.勾股定理
2.特殊到一般的探究过程和研究方法
3.证明勾股定理的一般思路
请按下暂停键,2分钟后再继续学习。
1.勾股定理
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
课堂小结
2.特殊到一般的探究过程和研究方法
等腰直角三角形→网格中的直角三角形→一般的直角三角形
课堂小结
3.证明勾股定理的一般思路
拼图的方法验证:
①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.
课堂小结
课后作业
1.必做:
(1)整理课堂中所提到的勾股定理的证明方法;
(2)完成课后作业中的题目.
2.选做:
上网查阅了解有关勾股定理的史料、趣事及其他证
明方法.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
勾股定理(第一课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
思考:
直角三角形的三边之间具有怎样的数量关系呢
在Rt△ABC中,∠C=90°,
∠A+ ∠B =90°.
探究一
我们也来观察一下地面的图案,你能发现三个正方形A,B ,C的面积之间有什么数量关系吗?
每块砖都是等腰直角三角形
请按下暂停键,1分钟后再继续学习。
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
每块砖都是等腰直角三角形
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
由这三个正方形A,B,C的边长构成的等腰直角三角形三条边长度之间有怎样的特殊关系?
探究一
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的大正方形的面积.
即等腰直角三角形的三边之间有一种特殊的关系:等腰直角三角形两直角边的平方和等于斜边的平方.
每块砖都是等腰直角三角形
相传2500多年前,毕达哥拉斯(约前580—约前500,古希腊著名的哲学家、数学家、天文学家.)有一次在朋友家做客时,发现朋友家用砖铺成的地面图案中反映了三个正方形A,B ,C的面积之间的数量关系,进而发现等腰直角三角形三边的某种数量关系.
探究一
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
请按下暂停键,5分钟后再继续学习。
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A
B
C
C
B
A
探究二
分割为四个直角三角形和一个小正方形.
正方形C的面积=13 .
探究二
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成一个正方形,图中两块红色(或绿色)可拼成一个小正方形.
探究二
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A的面积 B的面积 C的面积
左图
右图
4
9
16
9
13
请按下暂停键,3分钟后再继续学习。
A
B
C
C
B
A
探究二
观察右边两幅图:
在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C是否也有类似的面积关系?
填表(每个小方格的面积均为1)
A的面积 B的面积 C的面积
左图
右图
4
9
16
9
13
25
A
B
C
C
B
A
探究二
分析表中数据,你有什么发现?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
可以发现,以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.即直角三角形两直角边的平方和等于斜边的平方.
探究二
猜一猜:直角三角形三边之间应该有什么关系?
请按下暂停键,2分钟后再继续学习。
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
猜想
赵爽弦图证明法
b
a
赵爽拼图证明法:
以直角三角形的两条直角边a、b为边作两个正方形,
b
a
以直角三角形的两条直角边a,b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
赵爽拼图证明法:
c
b
a
图1
图2
赵爽弦图证明法
b
a
a
c
c
b
a
赵爽弦图证明法
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
“赵爽弦图”通过对图形的切割、拼接,巧妙地利用面积关系证明了勾股定理.
勾股定理
这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根据此图指出:四个全等的直角三角形(红色)可以如图围成一个大正方形,中间的部分是一个小正方形(黄色).
c
b
a
(
b
-
a
)
2
黄实
朱实
数学文化
勾股定理的证明方法很多,常见的是拼图的方法.
用拼图的方法验证勾股定理的思路是:
①图形经过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.
勾股定理的证明方法
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
为啥命名为勾股定理呢?
勾股定理
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代把直角三角形中较短的直角边称为“勾” ,较长的直角边称为“股” ,斜边称为“弦” .
勾股定理和人类文明
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三,股四,弦五”,它被记载于我国古代著名的数学著作《周髀算经》中.在我国勾股定理也叫做“商高定理” .
古希腊数学家毕达哥拉斯,在公元前5世纪给出了这个定理的证明,所以在国外这个定理也称为毕达哥拉斯定理,相传他证出这个定理后非常高兴,杀了一百头牛进行庆祝,于是也有人把它称为“百牛定理”.
勾股定理和人类文明
勾股定理的证明
1.传说中毕达哥拉斯的证法
请按下暂停键,2分钟后再继续学习。
1.传说中毕达哥拉斯的证法
勾股定理的证明
2.美国第20任总统加菲尔德的证法
勾股定理的证明
2.美国第20任总统加菲尔德的证法
试一试
请按下暂停键,2分钟后再继续学习。
勾股定理的证明
2.美国第20任总统加菲尔德的证法
化简得证:
,
,
.
勾股定理的证明
勾股定理在数学发展中起到了重大的作用,其证明方法据说有400多种,有兴趣的同学可以继续研究,或到网上查阅勾股定理的相关资料.
勾股定理的证明
练习1 求下列直角三角形中未知边的长度.
初步应用定理
(1)
(2)
请按下暂停键,2分钟后再继续学习。
练习1 求下列直角三角形中未知边的长度.
初步应用定理
(1)
(2)
答案: (1)8;(2)13.
练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
请按下暂停键,2分钟后再继续学习。
初步应用定理
练习2 如图,所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
答案: 625.
初步应用定理
通过这种方法,可以把一个正方形的面积分成若干个小正方形的面积的和,不断地分下去,就可以得到一棵美丽的勾股树.
初步应用定理
课堂小结
1.勾股定理
2.特殊到一般的探究过程和研究方法
3.证明勾股定理的一般思路
请按下暂停键,2分钟后再继续学习。
1.勾股定理
如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么 .
课堂小结
2.特殊到一般的探究过程和研究方法
等腰直角三角形→网格中的直角三角形→一般的直角三角形
课堂小结
3.证明勾股定理的一般思路
拼图的方法验证:
①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变;
②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.
课堂小结
课后作业
1.必做:
(1)整理课堂中所提到的勾股定理的证明方法;
(2)完成课后作业中的题目.
2.选做:
上网查阅了解有关勾股定理的史料、趣事及其他证
明方法.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
