2022-2023学年广东省华附、省实、广雅、深中四校联考高二(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年广东省华附、省实、广雅、深中四校联考高二(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 18:51:45 | ||
图片预览




文档简介
2022-2023学年广东省华附、省实、广雅、深中四校联考高二(下)期末数学试卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知i为虚数单位,z=1+i,则z2﹣|z|2=( )
A.0 B.2﹣2i C.2i﹣2 D.2i+2
2.(5分)已知集合M={x|0<ln(x+1)<3},N={y|y=sinx,x∈M},则M∩N=( )
A.[﹣1,1] B.(﹣1,1] C.(0,1] D.[0,1]
3.(5分)已知Sn为等差数列{an}的前n项和,若a1=3,且S8=a8,则a19=( )
A.﹣15 B.﹣18 C.﹣21 D.﹣22
4.(5分)已知向量,满足,且,记为在方向上的投影向量,则( )
A.4 B.3 C.2 D.1
5.(5分)小明将一颗质地均匀的骰子抛掷三次,观察向上一面的点数,已知三次点数都不相同,则三次点数之和不大于8的概率为( )
A. B. C. D.
6.(5分)已知双曲线C:1(a>0,b>0)的左,右焦点分别为F1,F2,O为坐标原点,过F1作C的一条渐近线的垂线,垂足为D,且|DF2|=2|OD|,则C的离心率为( )
A. B.2 C. D.3
7.(5分)已知定义在R上的函数f(x)满足:f(x﹣1)关于(1,0)中心对称,f(x+1)是偶函数,且.则下列选项中说法正确的有( )
A.f(x)为偶函数 B.f(x)周期为2
C. D.f(x﹣2)是奇函数
8.(5分)已知实数x,y满足ex=ylnx+ylny,则满足条件的y的最小值为( )
A.1 B.e C.2e D.e2
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
(多选)9.(5分)已知x>y>0,且x+y>1,则( )
A.x2>y2 B.x2﹣x<y2﹣y C.2x>2y D.lnx+lny>0
(多选)10.(5分)在平面直角坐标系xOy中,点P(1,0)绕点O逆时针旋转α后到达点Q(x0,y0),若,则x0可以取( )
A. B. C. D.
(多选)11.(5分)已知点P是圆C:x2+y2=8上的动点,直线x+y=4与x轴和y轴分别交于A,B两点,若△PAB为直角三角形,则点P的坐标可以是( )
A.(﹣2,﹣2) B.(﹣2,2) C. D.
(多选)12.(5分)如图,已知圆柱母线长为4,底面圆半径为,梯形ABCD内接于下底面圆,CD是直径,AB∥CD,AB=6,过点A,B,C,D向上底面作垂线,垂足分别为A1,B1,C1,D1,点M,N分别是线段CC1,AA1上的动点,点Q为上底面圆内(含边界)任意一点,则( )
A.若平面DMN交线段BB1于点R,则NR∥DM
B.若平面DMN过点B1,则直线MN过定点
C.△ABQ的周长为定值
D.当点Q在上底面圆周上运动时,记直线QA,QB与下底面所成角分别为α,β,则的取值范围是
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)“x<﹣1”是“x2﹣1>0”的 条件.
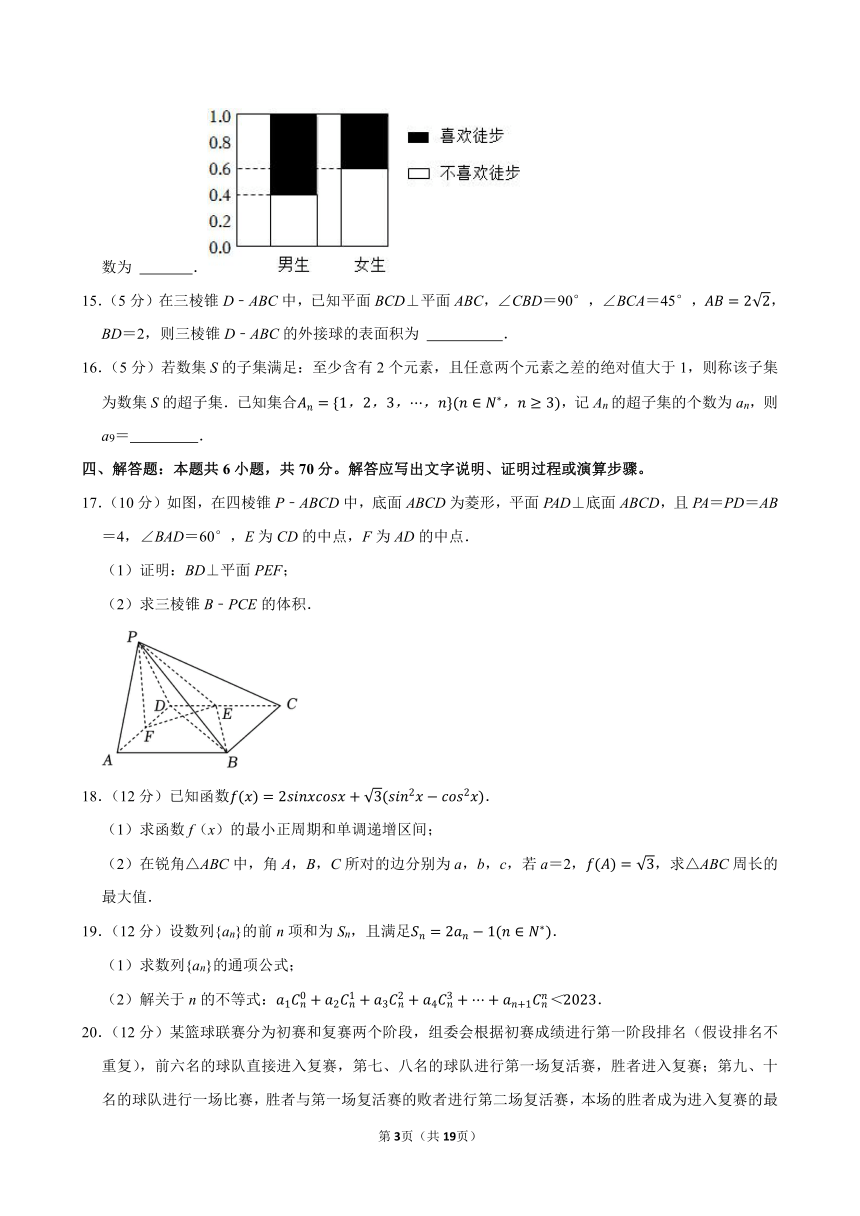
14.(5分)已知某学校高二年级有男生500人、女生450人,调查该年级全部男、女学生是否喜欢徒步运动的等高堆积条形图如图,现从所有喜欢徒步的学生中按分层抽样的方法抽取24人,则抽取的女生人数为 .
15.(5分)在三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,∠BCA=45°,,BD=2,则三棱锥D﹣ABC的外接球的表面积为 .
16.(5分)若数集S的子集满足:至少含有2个元素,且任意两个元素之差的绝对值大于1,则称该子集为数集S的超子集.已知集合,记An的超子集的个数为an,则a9= .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,平面PAD⊥底面ABCD,且PA=PD=AB=4,∠BAD=60°,E为CD的中点,F为AD的中点.
(1)证明:BD⊥平面PEF;
(2)求三棱锥B﹣PCE的体积.
18.(12分)已知函数.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若a=2,,求△ABC周长的最大值.
19.(12分)设数列{an}的前n项和为Sn,且满足.
(1)求数列{an}的通项公式;
(2)解关于n的不等式:.
20.(12分)某篮球联赛分为初赛和复赛两个阶段,组委会根据初赛成绩进行第一阶段排名(假设排名不重复),前六名的球队直接进入复赛,第七、八名的球队进行第一场复活赛,胜者进入复赛;第九、十名的球队进行一场比赛,胜者与第一场复活赛的败者进行第二场复活赛,本场的胜者成为进入复赛的最后一支球队.假设各场比赛结果互不影响,且每场比赛必须分出胜负.
(1)若初赛后,甲、乙、丙、丁四队分别排在第七、八、九、十名,丁队与甲、乙、丙队比赛获胜的概率分别是0.4,0.5,0.6,甲队与乙队比赛获胜的概率是0.6,则丁队进入复赛的概率是多少?
(2)若甲,乙两队进入复赛,在复赛中,甲队与乙队需进行一场五局三胜制的比赛,只要其中一方获胜三局,比赛结束、假设各局比赛结果互不影响.若乙队每局比赛获胜的概率为,设比赛结束时乙队获胜的局数为X,求X的概率分布列与均值.
21.(12分)设点F为抛物线C:x2=2py(p>0)的焦点,过点F且斜率为的直线与C交于A,B两点(O为坐标原点).
(1)求抛物线C的方程;
(2)过点E(0,2)作两条斜率分别为k1,k2的直线l1,l2,它们分别与抛物线C交于点P,Q和R,S.已知|EP| |EQ|=|ER| |ES|,问:是否存在实数λ,使得k1+λk2为定值?若存在,求λ的值,若不存在,请说明理由.
22.(12分)已知函数f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m.
(1)当m=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在[0,1]上存在两个零点x1,x2,证明:.
2022-2023学年广东省华附、省实、广雅、深中四校联考高二(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知i为虚数单位,z=1+i,则z2﹣|z|2=( )
A.0 B.2﹣2i C.2i﹣2 D.2i+2
【解答】解:z=1+i,
则z2=(1+i)2=2i,,
故z2﹣|z|2=2i﹣2=﹣2+2i.
故选:C.
2.(5分)已知集合M={x|0<ln(x+1)<3},N={y|y=sinx,x∈M},则M∩N=( )
A.[﹣1,1] B.(﹣1,1] C.(0,1] D.[0,1]
【解答】解:0<ln(x+1)<3,
则ln1<ln(x+1)<lne3,
故1<x+1<e3,解得0<x<e3﹣1,
所以N={y|y=sinx,x∈M}=(y|﹣1≤y≤1},
故M∩N=(0,1].
故选:C.
3.(5分)已知Sn为等差数列{an}的前n项和,若a1=3,且S8=a8,则a19=( )
A.﹣15 B.﹣18 C.﹣21 D.﹣22
【解答】解:等差数列{an}中,a1=3,且S8=a8,
所以8×3+28d=3+7d,
所以d=﹣1,
则a19=a1+18d=3﹣18=﹣15.
故选:A.
4.(5分)已知向量,满足,且,记为在方向上的投影向量,则( )
A.4 B.3 C.2 D.1
【解答】解:在方向上的投影向量为:
||cos||
(),
即(),故(),
则||3.
故选:B.
5.(5分)小明将一颗质地均匀的骰子抛掷三次,观察向上一面的点数,已知三次点数都不相同,则三次点数之和不大于8的概率为( )
A. B. C. D.
【解答】解:基本事件共120种,
三次点数之和不大于8包括{1,2,3},{1,2,4},{1,2,5},{1,3,4}共424种,
故P.
故选:D.
6.(5分)已知双曲线C:1(a>0,b>0)的左,右焦点分别为F1,F2,O为坐标原点,过F1作C的一条渐近线的垂线,垂足为D,且|DF2|=2|OD|,则C的离心率为( )
A. B.2 C. D.3
【解答】解:由双曲线的性质可知,双曲线的一条渐近线方程为yx,焦点F1(﹣c,0),F2(c,0),
由F1作该渐近线的垂线,则根据点到直线的距离公式可得:|DF1|=b,|OD|a,
∴|DF2|=2a,
由cos∠F1OD=﹣cos∠DOF2可得:0,
可得c2=5a2,则离心率e.
故选:C.
7.(5分)已知定义在R上的函数f(x)满足:f(x﹣1)关于(1,0)中心对称,f(x+1)是偶函数,且.则下列选项中说法正确的有( )
A.f(x)为偶函数 B.f(x)周期为2
C. D.f(x﹣2)是奇函数
【解答】解:由f(x﹣1)关于(1,0)中心对称,可得f(x﹣1)+f(2﹣x﹣1)=0,
即为f(x﹣1)+f(1﹣x)=0,即有f(﹣x)=﹣f(x),即f(x)为奇函数,故A错误;
由f(x+1)是偶函数,可得f(﹣x+1)=f(x+1),
即为f(﹣x)=f(x+2),
所以f(x+2)=﹣f(x),
则f(x+4)=﹣f(x+2)=f(x),
所以f(x)的周期为4,故B错误;
由f()=f(4)=f()=f()=﹣f()=﹣1,故C错误;
由f(x﹣2)=f(x+2)=﹣f(﹣x﹣2),可得f(x﹣2)为奇函数,故D正确.
故选:D.
8.(5分)已知实数x,y满足ex=ylnx+ylny,则满足条件的y的最小值为( )
A.1 B.e C.2e D.e2
【解答】解:由实数x,y满足ex=ylnx+ylny,可化为ex=yln(xy)(x>0,y>0,xy>1),即xex=xyln(xy)=ln(xy) eln(xy),
构造函数g(x)=xex,(x>0),g′(x)=(x+1)ex,
当x∈(0,+∞)时,g′(x)>0,g(x)单调递增,
即g(x)=g(ln(xy)),可以得到x=ln(xy),
从而,构造函数,
,令h′(x)=0可以得到x=1,
当x∈(0,1)时,h′(x)<0,h(x)单调递减,
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增,
从而当x=1时,h(x)取最小值h(1)=e,即y有最小值e.
故选:B.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
(多选)9.(5分)已知x>y>0,且x+y>1,则( )
A.x2>y2 B.x2﹣x<y2﹣y C.2x>2y D.lnx+lny>0
【解答】解:对于A,因为x>y>0,所以x2>y2,即选项A正确;
对于B,不妨取x=2,y=1,则x2﹣x=4﹣2=2,y2﹣y=1﹣1=0,此时x2﹣x>y2﹣y,即选项B错误;
对于C,因为函数y=2x单调递增,所以2x>2y,即选项C正确;
对于D,不妨取x=2,y,则lnx+lny=ln(xy)=ln(2)=ln1=0,即选项D错误.
故选:AC.
(多选)10.(5分)在平面直角坐标系xOy中,点P(1,0)绕点O逆时针旋转α后到达点Q(x0,y0),若,则x0可以取( )
A. B. C. D.
【解答】解:因为,所以2cos(α),即cos(α),
当α是第二象限角时,sin(α),
所以cosα=cos[(α)]=cos(α)cossin(α)sin,
所以x0=cosα;
当α是第三象限角时,sin(α),
所以cosα=cos[(α)]=cos(α)cossin(α)sin(),
所以x0=cosα,
综上,x0的可能取值为或.
故选:AD.
(多选)11.(5分)已知点P是圆C:x2+y2=8上的动点,直线x+y=4与x轴和y轴分别交于A,B两点,若△PAB为直角三角形,则点P的坐标可以是( )
A.(﹣2,﹣2) B.(﹣2,2) C. D.
【解答】解:由题可得A(4,0),B(0,4),设P(x,y),
当∠PAB为直角时,,,
∴,
即(x﹣4)×(﹣4)+4y=0,即x﹣y﹣4=0,
又x2+y2=8,∴,∴此时P(2,﹣2);
当∠ABP为直角时,,,
∴0,
即(﹣4)x+4(y﹣4)=0,即x﹣y+4=0,
又x2+y2=8,∴,∴此时P(﹣2,2);
当∠APB为直角时,,,
∵,
即x(x﹣4)+y(y﹣4)=0,即x2﹣4x+y2﹣4y=0,
又x2+y2=8,∴或,∴此时P(1,1)或(,1).
故选:BCD.
(多选)12.(5分)如图,已知圆柱母线长为4,底面圆半径为,梯形ABCD内接于下底面圆,CD是直径,AB∥CD,AB=6,过点A,B,C,D向上底面作垂线,垂足分别为A1,B1,C1,D1,点M,N分别是线段CC1,AA1上的动点,点Q为上底面圆内(含边界)任意一点,则( )
A.若平面DMN交线段BB1于点R,则NR∥DM
B.若平面DMN过点B1,则直线MN过定点
C.△ABQ的周长为定值
D.当点Q在上底面圆周上运动时,记直线QA,QB与下底面所成角分别为α,β,则的取值范围是
【解答】解:A:由题可得DC∥AB,AB 面ABB1A1,DC 面ABB1A1,故DC∥面ABB1A1;
又CC1∥BB1,BB1 面ABB1A1,CC1 面ABB1A1,故CC1∥面ABB1A1;
DC∩CC1=C,DC,CC1 面DCC1D1,故面DCC1D1∥面ABB1A1;
又DM 面DCC1D1,故DM∥面ABB1A1;
又DM 面DMN,面DMN∩面ABB1A1=NR,故可得DM∥NR,故A正确;
B:根据题意,DB1,MN共面,
又M、N分别为CC1,AA1上的动点,故直线MN 面ACC1A1;
不妨设直线DB1与平面ACC1A1的交点为P,
若要满足DB1与MN共面,则直线MN必过点P,又P为定点,故B正确;
C:设△ABQ的周长为l,
当点Q与B1重合时,;
当点Q与A1B1中点重合时,连接BQ,AQ:
此时l=AB+BQ+AQ=AB+2BQ=66+26+10=16;
显然△ABO周长不为定值,故C错误;
D:过O作底面垂线,垂足为E,且在下底面圆周上,即QE⊥面ABCD,
连接BE,AE,则∠QBE,∠QAE分别是直线QA,QB与下底面所成的角,
∴sinα,cosα,sinβ,cosβ,
则,,
则,
∵QE=4,AB=6,底面圆半径为2,
若E在AB对应优弧上时,∠AEB,则cos∠AEB,
∴AE2+BE2﹣AE BE=36,当且仅当AE=BE=6时,等号成立,此时AE2+BE2≤72,
若E在AB对应劣弧上时,∠AEB,则cos∠AEB,
∴AE2+BE2+AE BE=36,当且仅当AE=BE=2时等号成立,
此时AE2+BE2≥24,
综上24≤AE2+BE2≤72,,
故∈[,],故 D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)“x<﹣1”是“x2﹣1>0”的 充分不必要 条件.
【解答】解析:x2﹣1>0 x>1或x<﹣1,故x<﹣1 x2﹣1>0,
但x2﹣1>0不能得出x<﹣1,
∴“x<﹣1”是“x2﹣1>0”的充分不必要条件.
故答案为:充分不必要
14.(5分)已知某学校高二年级有男生500人、女生450人,调查该年级全部男、女学生是否喜欢徒步运动的等高堆积条形图如图,现从所有喜欢徒步的学生中按分层抽样的方法抽取24人,则抽取的女生人数为 9 .
【解答】解:由等高堆积条形图可得喜欢徒步的男生有500×0.6=300人,喜欢徒步的女生有450×0.4=180人.
故喜欢徒步的总人数为300+180=480人.
按分层抽样的方法抽取24人,则抽取的女生人数为人.
故答案为:9.
15.(5分)在三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,∠BCA=45°,,BD=2,则三棱锥D﹣ABC的外接球的表面积为 20π .
【解答】解:如图所示:
三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,
所以BD⊥BC,
故BD⊥平面ABC,
故AB⊥BD,
∠BCA=45°,,BD=2,
在△ABC中,有2R,
所以外接圆的半径为2,
由于平面BCD⊥平面ABC,且其交线为BC,
所以BD⊥BC,故BD⊥平面ABC,
所以三棱锥D﹣ABC的外接球的半径为r,
故外接球的表面积.
故答案为:20π.
16.(5分)若数集S的子集满足:至少含有2个元素,且任意两个元素之差的绝对值大于1,则称该子集为数集S的超子集.已知集合,记An的超子集的个数为an,则a9= 79 .
【解答】解:集合{1,2,3,…,k,k+1,k+2}(k∈N*)的超子集可以分为两类:
第一类中不含有k+2,这类子集有ak+1个,
第二类子集中含有k+2,这类子集为{1,2,3,.…,k}的超子集与{k+2}的并集,共有ak+k个,
∴ak+2=ak+1+ak+k,
∵a3=1,a4=3,
∴a5=7,a6=14,a7=26,a8=46,a9=79.
故答案为:79.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,平面PAD⊥底面ABCD,且PA=PD=AB=4,∠BAD=60°,E为CD的中点,F为AD的中点.
(1)证明:BD⊥平面PEF;
(2)求三棱锥B﹣PCE的体积.
【解答】(1)证明:连接AC,如图所示,
因为底面ABCD为菱形,所以AC⊥BD,
又因为E为CD的中点,F为AD的中点,所以EF∥AC,所以BD⊥EF,
因为PA=PD,F为AD的中点.所以PF⊥AD,
又因为平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
所以PF⊥平面ABCD,
又因为BD 平面ABCD,所以PF⊥BD,
且EF∩PF=F,EF 平面PEF,PF 平面PEF,
所以BD⊥平面PEF.
(2)解:AB=BC=4,CECD=2,∠BCE=60°,
所以S△BCEBC CE sin60°4×22,
又因为PA=PD=AD=4,所以PFAD=2,
所以三棱锥B﹣PCE的体积为:
V三棱锥B﹣PCE=V三棱锥P﹣BCES△BCE PF224.
18.(12分)已知函数.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若a=2,,求△ABC周长的最大值.
【解答】解:(1),
函数的最小正周期为,
由,得,
即函数f(x)的单调递增区间为;
(2)∵,
∴,
因为,
所以,
所以,
∴,
又a=2,由余弦定理可得b2+c2﹣a2=2bccosA=bc,
即(b+c)2﹣2bc﹣4=bc,
则4,则,
∴b+c≤4,
∴a+b+c≤6,
所以△ABC周长最大值为6.
19.(12分)设数列{an}的前n项和为Sn,且满足.
(1)求数列{an}的通项公式;
(2)解关于n的不等式:.
【解答】解:(1)由知当n≥2,有Sn﹣1=2an﹣1﹣1,
二式相减得an=2an﹣2an﹣1,即an=2an﹣1,
又S1=2a1﹣1=a1,解得a1=1,
所以数列{an}是以1为首项,2为公比的等比数列,
所以an=2n﹣1;
(2)结合(1)知原式=1222232n(1+2)n=3n,
由于3n随着n的增大而增大,
且36=729<2023,37=2187>2023,
所以正整数n最大可取6,
即原不等式的解集为{n|n≤6,n∈N*}.
20.(12分)某篮球联赛分为初赛和复赛两个阶段,组委会根据初赛成绩进行第一阶段排名(假设排名不重复),前六名的球队直接进入复赛,第七、八名的球队进行第一场复活赛,胜者进入复赛;第九、十名的球队进行一场比赛,胜者与第一场复活赛的败者进行第二场复活赛,本场的胜者成为进入复赛的最后一支球队.假设各场比赛结果互不影响,且每场比赛必须分出胜负.
(1)若初赛后,甲、乙、丙、丁四队分别排在第七、八、九、十名,丁队与甲、乙、丙队比赛获胜的概率分别是0.4,0.5,0.6,甲队与乙队比赛获胜的概率是0.6,则丁队进入复赛的概率是多少?
(2)若甲,乙两队进入复赛,在复赛中,甲队与乙队需进行一场五局三胜制的比赛,只要其中一方获胜三局,比赛结束、假设各局比赛结果互不影响.若乙队每局比赛获胜的概率为,设比赛结束时乙队获胜的局数为X,求X的概率分布列与均值.
【解答】解:(1)依题意,记丁队进入复赛的事件为A,丁队进入复赛需参加两场比赛,第一场战胜丙队,记为事件A1,
第二场战胜甲乙比赛中的败者,记为事件A2,甲队战胜乙队记为事件B,
则P(A1)=0.6,P(B)=0.6,P()=0.4,,
因此0.6×0.5+0.4×0.4=0.46,
所以P(A)=P(A1)P(A2)=0.6×0.46=0.276.
(2)依题意,X的可能值为0,1,2,3,
,,
,,
所以X的概率分布列为:
X 0 1 2 3
P
数学期望为.
21.(12分)设点F为抛物线C:x2=2py(p>0)的焦点,过点F且斜率为的直线与C交于A,B两点(O为坐标原点).
(1)求抛物线C的方程;
(2)过点E(0,2)作两条斜率分别为k1,k2的直线l1,l2,它们分别与抛物线C交于点P,Q和R,S.已知|EP| |EQ|=|ER| |ES|,问:是否存在实数λ,使得k1+λk2为定值?若存在,求λ的值,若不存在,请说明理由.
【解答】解:(1)抛物线C:x2=2py(p>0)的焦点为F(0,),
直线AB的方程yx,
由,得x2﹣2py﹣p2=0,
设A(x1,y1),B(x2,y2),
所以x1+x2=2p,x1x2=﹣p2,
所以|x1﹣x2|2p,
所以S△AOB|OF||x1﹣x2|2p=2,p>0,
所以p=2,
所以抛物线C的方程为x2=4y.
(2)存在λ=1,使得k1+λk2为定值,
由题意可得直线l1的方程y=k1x+2,直线l2的方程为y=k2x+2,
联立,得x2﹣4k1x﹣8=0,
设P(x3,y3),Q(x4,y4),
所以x3+x4=4k1,x3x4=﹣8,
|EP||x3|,|EQ||x4|,
所以|EP| |EQ|=8(1),
设R(x5,y5),S(x6,y6),
同理可得x5+x6=4k2,x5x6=﹣8,
所以|ER| |ES|=8(1),
由|EP| |EQ|=|ER| |ES|,得8(1)=8(1),
即,而k1≠k2,
所以k1+k2=0,
所以存在λ=1,使得k1+λk2为定值0.
22.(12分)已知函数f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m.
(1)当m=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在[0,1]上存在两个零点x1,x2,证明:.
【解答】解:(1)已知f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m,函数定义域为(﹣1,+∞),
当m=0时,f(x)=sinπx﹣3(x﹣1)ln(x+1),
可得,
此时f′(0)=π+3,
又f(0)=0,
所以f(x)在x=0处的切线方程为y﹣0=(π+3)(x﹣0),
即y=(π+3)x;
(2)证明:不妨设g(x)=sinπx﹣3(x﹣1)ln(x+1),函数定义域为(﹣1,+∞),
若f(x)在[0,1]上存在两个零点x1,x2,
此时g(x)=m在[0,1]上存在两个零点x1,x2,
可得,
不妨设h(x)=g′(x),
可得h′(x)=﹣π2sinπxπ2sinπx,
易知对任意的x∈[0,1],都有sinπx>0,
所以对任意的x∈[0,1],h′(x)<0恒成立,
则g′(x)在[0,1]上单调递减,
又g′(0)=π+3,g′(1)=﹣π﹣3ln2<0,
所以存在x0∈(0,1),使得g′(x0)=0,
当0≤x<x0时,g′(x)>0,g(x)单调递增;
当x0<x≤1时,g′(x)<0,g(x)单调递减,
所以当x=x0时,函数g(x)取到极大值,极大值g(x0)=sinπx0﹣3(x0﹣1)ln(x0+1)>0,
又g(0)=g(1)=0,
所以当且仅当0≤m<sinπx0﹣3(x0﹣1)ln(x0+1)时,
g(x)=m在[0,x0)和(x0,1]上各恰有一个零点,分别为x1,x2,
不妨设x1<x2,
由(1)知,g(x)在x=0处的切线方程为y=(π+3)x,
不妨设k(x)=g(x)﹣(π+3)x,
可得k′(x)=g′(x)﹣(π+3)=h(x)﹣(π+3),
不妨设m(x)=k′(x),
可得m′(x)=h′(x)<0,
所以m(x)在[0,1]上单调递减,
即k(x)在[0,1]上单调递减,
又k′(0)=g′(0)﹣(π+3)=0,
所以对任意x∈[0,1],都有k′(x)≤0,
则k(x)在[0,1]上单调递减,
又k(0)=g(0)=0,
所以对任意的x∈[0,1],都有k(x)≤0,
则当x∈[0,1]时,g(x)≤(π+3)x;
同理得,g(x)在x=1处的切线方程为y=(π+3ln2)(1﹣x),
不妨设n(x)=g(x)﹣(π+3ln2)(1﹣x),
可得n′(x)=g′(x)+(π+3ln2)=h(x)+(π+3ln2),
不妨设p(x)=n′(x),
可得p′(x)=h′(x)<0,
所以n′(x)在[0,1]单调递减,
又n′(1)=g′(1)+(π+3ln2)=0,
所以对任意x∈[0,1],都有n′(x)≥0,
则n(x)在[0,1]上单调递增,
又n(1)=g(1)=0,
所以对任意x∈[0,1],都有n(x)≤0,
则当x∈[0,1]时,g(x)≤(π+3ln2)(1﹣x),
不妨设(π+3)x=m和(π+3ln2)(1﹣x)=m的零点分别为,,
因为(π+3)x3=m=g(x1)≤(π+3)x1,
所以x3≤x1,
因为(π+3ln2)(1﹣x4)=m=g(x2)≤(π+3ln2)(1﹣x2),
所以x4≥x2,
则x3≤x1<x2≤x4,
故|x1﹣x2|≤x4﹣x3=11.
第1页(共1页)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知i为虚数单位,z=1+i,则z2﹣|z|2=( )
A.0 B.2﹣2i C.2i﹣2 D.2i+2
2.(5分)已知集合M={x|0<ln(x+1)<3},N={y|y=sinx,x∈M},则M∩N=( )
A.[﹣1,1] B.(﹣1,1] C.(0,1] D.[0,1]
3.(5分)已知Sn为等差数列{an}的前n项和,若a1=3,且S8=a8,则a19=( )
A.﹣15 B.﹣18 C.﹣21 D.﹣22
4.(5分)已知向量,满足,且,记为在方向上的投影向量,则( )
A.4 B.3 C.2 D.1
5.(5分)小明将一颗质地均匀的骰子抛掷三次,观察向上一面的点数,已知三次点数都不相同,则三次点数之和不大于8的概率为( )
A. B. C. D.
6.(5分)已知双曲线C:1(a>0,b>0)的左,右焦点分别为F1,F2,O为坐标原点,过F1作C的一条渐近线的垂线,垂足为D,且|DF2|=2|OD|,则C的离心率为( )
A. B.2 C. D.3
7.(5分)已知定义在R上的函数f(x)满足:f(x﹣1)关于(1,0)中心对称,f(x+1)是偶函数,且.则下列选项中说法正确的有( )
A.f(x)为偶函数 B.f(x)周期为2
C. D.f(x﹣2)是奇函数
8.(5分)已知实数x,y满足ex=ylnx+ylny,则满足条件的y的最小值为( )
A.1 B.e C.2e D.e2
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
(多选)9.(5分)已知x>y>0,且x+y>1,则( )
A.x2>y2 B.x2﹣x<y2﹣y C.2x>2y D.lnx+lny>0
(多选)10.(5分)在平面直角坐标系xOy中,点P(1,0)绕点O逆时针旋转α后到达点Q(x0,y0),若,则x0可以取( )
A. B. C. D.
(多选)11.(5分)已知点P是圆C:x2+y2=8上的动点,直线x+y=4与x轴和y轴分别交于A,B两点,若△PAB为直角三角形,则点P的坐标可以是( )
A.(﹣2,﹣2) B.(﹣2,2) C. D.
(多选)12.(5分)如图,已知圆柱母线长为4,底面圆半径为,梯形ABCD内接于下底面圆,CD是直径,AB∥CD,AB=6,过点A,B,C,D向上底面作垂线,垂足分别为A1,B1,C1,D1,点M,N分别是线段CC1,AA1上的动点,点Q为上底面圆内(含边界)任意一点,则( )
A.若平面DMN交线段BB1于点R,则NR∥DM
B.若平面DMN过点B1,则直线MN过定点
C.△ABQ的周长为定值
D.当点Q在上底面圆周上运动时,记直线QA,QB与下底面所成角分别为α,β,则的取值范围是
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)“x<﹣1”是“x2﹣1>0”的 条件.
14.(5分)已知某学校高二年级有男生500人、女生450人,调查该年级全部男、女学生是否喜欢徒步运动的等高堆积条形图如图,现从所有喜欢徒步的学生中按分层抽样的方法抽取24人,则抽取的女生人数为 .
15.(5分)在三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,∠BCA=45°,,BD=2,则三棱锥D﹣ABC的外接球的表面积为 .
16.(5分)若数集S的子集满足:至少含有2个元素,且任意两个元素之差的绝对值大于1,则称该子集为数集S的超子集.已知集合,记An的超子集的个数为an,则a9= .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,平面PAD⊥底面ABCD,且PA=PD=AB=4,∠BAD=60°,E为CD的中点,F为AD的中点.
(1)证明:BD⊥平面PEF;
(2)求三棱锥B﹣PCE的体积.
18.(12分)已知函数.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若a=2,,求△ABC周长的最大值.
19.(12分)设数列{an}的前n项和为Sn,且满足.
(1)求数列{an}的通项公式;
(2)解关于n的不等式:.
20.(12分)某篮球联赛分为初赛和复赛两个阶段,组委会根据初赛成绩进行第一阶段排名(假设排名不重复),前六名的球队直接进入复赛,第七、八名的球队进行第一场复活赛,胜者进入复赛;第九、十名的球队进行一场比赛,胜者与第一场复活赛的败者进行第二场复活赛,本场的胜者成为进入复赛的最后一支球队.假设各场比赛结果互不影响,且每场比赛必须分出胜负.
(1)若初赛后,甲、乙、丙、丁四队分别排在第七、八、九、十名,丁队与甲、乙、丙队比赛获胜的概率分别是0.4,0.5,0.6,甲队与乙队比赛获胜的概率是0.6,则丁队进入复赛的概率是多少?
(2)若甲,乙两队进入复赛,在复赛中,甲队与乙队需进行一场五局三胜制的比赛,只要其中一方获胜三局,比赛结束、假设各局比赛结果互不影响.若乙队每局比赛获胜的概率为,设比赛结束时乙队获胜的局数为X,求X的概率分布列与均值.
21.(12分)设点F为抛物线C:x2=2py(p>0)的焦点,过点F且斜率为的直线与C交于A,B两点(O为坐标原点).
(1)求抛物线C的方程;
(2)过点E(0,2)作两条斜率分别为k1,k2的直线l1,l2,它们分别与抛物线C交于点P,Q和R,S.已知|EP| |EQ|=|ER| |ES|,问:是否存在实数λ,使得k1+λk2为定值?若存在,求λ的值,若不存在,请说明理由.
22.(12分)已知函数f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m.
(1)当m=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在[0,1]上存在两个零点x1,x2,证明:.
2022-2023学年广东省华附、省实、广雅、深中四校联考高二(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知i为虚数单位,z=1+i,则z2﹣|z|2=( )
A.0 B.2﹣2i C.2i﹣2 D.2i+2
【解答】解:z=1+i,
则z2=(1+i)2=2i,,
故z2﹣|z|2=2i﹣2=﹣2+2i.
故选:C.
2.(5分)已知集合M={x|0<ln(x+1)<3},N={y|y=sinx,x∈M},则M∩N=( )
A.[﹣1,1] B.(﹣1,1] C.(0,1] D.[0,1]
【解答】解:0<ln(x+1)<3,
则ln1<ln(x+1)<lne3,
故1<x+1<e3,解得0<x<e3﹣1,
所以N={y|y=sinx,x∈M}=(y|﹣1≤y≤1},
故M∩N=(0,1].
故选:C.
3.(5分)已知Sn为等差数列{an}的前n项和,若a1=3,且S8=a8,则a19=( )
A.﹣15 B.﹣18 C.﹣21 D.﹣22
【解答】解:等差数列{an}中,a1=3,且S8=a8,
所以8×3+28d=3+7d,
所以d=﹣1,
则a19=a1+18d=3﹣18=﹣15.
故选:A.
4.(5分)已知向量,满足,且,记为在方向上的投影向量,则( )
A.4 B.3 C.2 D.1
【解答】解:在方向上的投影向量为:
||cos||
(),
即(),故(),
则||3.
故选:B.
5.(5分)小明将一颗质地均匀的骰子抛掷三次,观察向上一面的点数,已知三次点数都不相同,则三次点数之和不大于8的概率为( )
A. B. C. D.
【解答】解:基本事件共120种,
三次点数之和不大于8包括{1,2,3},{1,2,4},{1,2,5},{1,3,4}共424种,
故P.
故选:D.
6.(5分)已知双曲线C:1(a>0,b>0)的左,右焦点分别为F1,F2,O为坐标原点,过F1作C的一条渐近线的垂线,垂足为D,且|DF2|=2|OD|,则C的离心率为( )
A. B.2 C. D.3
【解答】解:由双曲线的性质可知,双曲线的一条渐近线方程为yx,焦点F1(﹣c,0),F2(c,0),
由F1作该渐近线的垂线,则根据点到直线的距离公式可得:|DF1|=b,|OD|a,
∴|DF2|=2a,
由cos∠F1OD=﹣cos∠DOF2可得:0,
可得c2=5a2,则离心率e.
故选:C.
7.(5分)已知定义在R上的函数f(x)满足:f(x﹣1)关于(1,0)中心对称,f(x+1)是偶函数,且.则下列选项中说法正确的有( )
A.f(x)为偶函数 B.f(x)周期为2
C. D.f(x﹣2)是奇函数
【解答】解:由f(x﹣1)关于(1,0)中心对称,可得f(x﹣1)+f(2﹣x﹣1)=0,
即为f(x﹣1)+f(1﹣x)=0,即有f(﹣x)=﹣f(x),即f(x)为奇函数,故A错误;
由f(x+1)是偶函数,可得f(﹣x+1)=f(x+1),
即为f(﹣x)=f(x+2),
所以f(x+2)=﹣f(x),
则f(x+4)=﹣f(x+2)=f(x),
所以f(x)的周期为4,故B错误;
由f()=f(4)=f()=f()=﹣f()=﹣1,故C错误;
由f(x﹣2)=f(x+2)=﹣f(﹣x﹣2),可得f(x﹣2)为奇函数,故D正确.
故选:D.
8.(5分)已知实数x,y满足ex=ylnx+ylny,则满足条件的y的最小值为( )
A.1 B.e C.2e D.e2
【解答】解:由实数x,y满足ex=ylnx+ylny,可化为ex=yln(xy)(x>0,y>0,xy>1),即xex=xyln(xy)=ln(xy) eln(xy),
构造函数g(x)=xex,(x>0),g′(x)=(x+1)ex,
当x∈(0,+∞)时,g′(x)>0,g(x)单调递增,
即g(x)=g(ln(xy)),可以得到x=ln(xy),
从而,构造函数,
,令h′(x)=0可以得到x=1,
当x∈(0,1)时,h′(x)<0,h(x)单调递减,
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增,
从而当x=1时,h(x)取最小值h(1)=e,即y有最小值e.
故选:B.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
(多选)9.(5分)已知x>y>0,且x+y>1,则( )
A.x2>y2 B.x2﹣x<y2﹣y C.2x>2y D.lnx+lny>0
【解答】解:对于A,因为x>y>0,所以x2>y2,即选项A正确;
对于B,不妨取x=2,y=1,则x2﹣x=4﹣2=2,y2﹣y=1﹣1=0,此时x2﹣x>y2﹣y,即选项B错误;
对于C,因为函数y=2x单调递增,所以2x>2y,即选项C正确;
对于D,不妨取x=2,y,则lnx+lny=ln(xy)=ln(2)=ln1=0,即选项D错误.
故选:AC.
(多选)10.(5分)在平面直角坐标系xOy中,点P(1,0)绕点O逆时针旋转α后到达点Q(x0,y0),若,则x0可以取( )
A. B. C. D.
【解答】解:因为,所以2cos(α),即cos(α),
当α是第二象限角时,sin(α),
所以cosα=cos[(α)]=cos(α)cossin(α)sin,
所以x0=cosα;
当α是第三象限角时,sin(α),
所以cosα=cos[(α)]=cos(α)cossin(α)sin(),
所以x0=cosα,
综上,x0的可能取值为或.
故选:AD.
(多选)11.(5分)已知点P是圆C:x2+y2=8上的动点,直线x+y=4与x轴和y轴分别交于A,B两点,若△PAB为直角三角形,则点P的坐标可以是( )
A.(﹣2,﹣2) B.(﹣2,2) C. D.
【解答】解:由题可得A(4,0),B(0,4),设P(x,y),
当∠PAB为直角时,,,
∴,
即(x﹣4)×(﹣4)+4y=0,即x﹣y﹣4=0,
又x2+y2=8,∴,∴此时P(2,﹣2);
当∠ABP为直角时,,,
∴0,
即(﹣4)x+4(y﹣4)=0,即x﹣y+4=0,
又x2+y2=8,∴,∴此时P(﹣2,2);
当∠APB为直角时,,,
∵,
即x(x﹣4)+y(y﹣4)=0,即x2﹣4x+y2﹣4y=0,
又x2+y2=8,∴或,∴此时P(1,1)或(,1).
故选:BCD.
(多选)12.(5分)如图,已知圆柱母线长为4,底面圆半径为,梯形ABCD内接于下底面圆,CD是直径,AB∥CD,AB=6,过点A,B,C,D向上底面作垂线,垂足分别为A1,B1,C1,D1,点M,N分别是线段CC1,AA1上的动点,点Q为上底面圆内(含边界)任意一点,则( )
A.若平面DMN交线段BB1于点R,则NR∥DM
B.若平面DMN过点B1,则直线MN过定点
C.△ABQ的周长为定值
D.当点Q在上底面圆周上运动时,记直线QA,QB与下底面所成角分别为α,β,则的取值范围是
【解答】解:A:由题可得DC∥AB,AB 面ABB1A1,DC 面ABB1A1,故DC∥面ABB1A1;
又CC1∥BB1,BB1 面ABB1A1,CC1 面ABB1A1,故CC1∥面ABB1A1;
DC∩CC1=C,DC,CC1 面DCC1D1,故面DCC1D1∥面ABB1A1;
又DM 面DCC1D1,故DM∥面ABB1A1;
又DM 面DMN,面DMN∩面ABB1A1=NR,故可得DM∥NR,故A正确;
B:根据题意,DB1,MN共面,
又M、N分别为CC1,AA1上的动点,故直线MN 面ACC1A1;
不妨设直线DB1与平面ACC1A1的交点为P,
若要满足DB1与MN共面,则直线MN必过点P,又P为定点,故B正确;
C:设△ABQ的周长为l,
当点Q与B1重合时,;
当点Q与A1B1中点重合时,连接BQ,AQ:
此时l=AB+BQ+AQ=AB+2BQ=66+26+10=16;
显然△ABO周长不为定值,故C错误;
D:过O作底面垂线,垂足为E,且在下底面圆周上,即QE⊥面ABCD,
连接BE,AE,则∠QBE,∠QAE分别是直线QA,QB与下底面所成的角,
∴sinα,cosα,sinβ,cosβ,
则,,
则,
∵QE=4,AB=6,底面圆半径为2,
若E在AB对应优弧上时,∠AEB,则cos∠AEB,
∴AE2+BE2﹣AE BE=36,当且仅当AE=BE=6时,等号成立,此时AE2+BE2≤72,
若E在AB对应劣弧上时,∠AEB,则cos∠AEB,
∴AE2+BE2+AE BE=36,当且仅当AE=BE=2时等号成立,
此时AE2+BE2≥24,
综上24≤AE2+BE2≤72,,
故∈[,],故 D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.(5分)“x<﹣1”是“x2﹣1>0”的 充分不必要 条件.
【解答】解析:x2﹣1>0 x>1或x<﹣1,故x<﹣1 x2﹣1>0,
但x2﹣1>0不能得出x<﹣1,
∴“x<﹣1”是“x2﹣1>0”的充分不必要条件.
故答案为:充分不必要
14.(5分)已知某学校高二年级有男生500人、女生450人,调查该年级全部男、女学生是否喜欢徒步运动的等高堆积条形图如图,现从所有喜欢徒步的学生中按分层抽样的方法抽取24人,则抽取的女生人数为 9 .
【解答】解:由等高堆积条形图可得喜欢徒步的男生有500×0.6=300人,喜欢徒步的女生有450×0.4=180人.
故喜欢徒步的总人数为300+180=480人.
按分层抽样的方法抽取24人,则抽取的女生人数为人.
故答案为:9.
15.(5分)在三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,∠BCA=45°,,BD=2,则三棱锥D﹣ABC的外接球的表面积为 20π .
【解答】解:如图所示:
三棱锥D﹣ABC中,已知平面BCD⊥平面ABC,∠CBD=90°,
所以BD⊥BC,
故BD⊥平面ABC,
故AB⊥BD,
∠BCA=45°,,BD=2,
在△ABC中,有2R,
所以外接圆的半径为2,
由于平面BCD⊥平面ABC,且其交线为BC,
所以BD⊥BC,故BD⊥平面ABC,
所以三棱锥D﹣ABC的外接球的半径为r,
故外接球的表面积.
故答案为:20π.
16.(5分)若数集S的子集满足:至少含有2个元素,且任意两个元素之差的绝对值大于1,则称该子集为数集S的超子集.已知集合,记An的超子集的个数为an,则a9= 79 .
【解答】解:集合{1,2,3,…,k,k+1,k+2}(k∈N*)的超子集可以分为两类:
第一类中不含有k+2,这类子集有ak+1个,
第二类子集中含有k+2,这类子集为{1,2,3,.…,k}的超子集与{k+2}的并集,共有ak+k个,
∴ak+2=ak+1+ak+k,
∵a3=1,a4=3,
∴a5=7,a6=14,a7=26,a8=46,a9=79.
故答案为:79.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,平面PAD⊥底面ABCD,且PA=PD=AB=4,∠BAD=60°,E为CD的中点,F为AD的中点.
(1)证明:BD⊥平面PEF;
(2)求三棱锥B﹣PCE的体积.
【解答】(1)证明:连接AC,如图所示,
因为底面ABCD为菱形,所以AC⊥BD,
又因为E为CD的中点,F为AD的中点,所以EF∥AC,所以BD⊥EF,
因为PA=PD,F为AD的中点.所以PF⊥AD,
又因为平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
所以PF⊥平面ABCD,
又因为BD 平面ABCD,所以PF⊥BD,
且EF∩PF=F,EF 平面PEF,PF 平面PEF,
所以BD⊥平面PEF.
(2)解:AB=BC=4,CECD=2,∠BCE=60°,
所以S△BCEBC CE sin60°4×22,
又因为PA=PD=AD=4,所以PFAD=2,
所以三棱锥B﹣PCE的体积为:
V三棱锥B﹣PCE=V三棱锥P﹣BCES△BCE PF224.
18.(12分)已知函数.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若a=2,,求△ABC周长的最大值.
【解答】解:(1),
函数的最小正周期为,
由,得,
即函数f(x)的单调递增区间为;
(2)∵,
∴,
因为,
所以,
所以,
∴,
又a=2,由余弦定理可得b2+c2﹣a2=2bccosA=bc,
即(b+c)2﹣2bc﹣4=bc,
则4,则,
∴b+c≤4,
∴a+b+c≤6,
所以△ABC周长最大值为6.
19.(12分)设数列{an}的前n项和为Sn,且满足.
(1)求数列{an}的通项公式;
(2)解关于n的不等式:.
【解答】解:(1)由知当n≥2,有Sn﹣1=2an﹣1﹣1,
二式相减得an=2an﹣2an﹣1,即an=2an﹣1,
又S1=2a1﹣1=a1,解得a1=1,
所以数列{an}是以1为首项,2为公比的等比数列,
所以an=2n﹣1;
(2)结合(1)知原式=1222232n(1+2)n=3n,
由于3n随着n的增大而增大,
且36=729<2023,37=2187>2023,
所以正整数n最大可取6,
即原不等式的解集为{n|n≤6,n∈N*}.
20.(12分)某篮球联赛分为初赛和复赛两个阶段,组委会根据初赛成绩进行第一阶段排名(假设排名不重复),前六名的球队直接进入复赛,第七、八名的球队进行第一场复活赛,胜者进入复赛;第九、十名的球队进行一场比赛,胜者与第一场复活赛的败者进行第二场复活赛,本场的胜者成为进入复赛的最后一支球队.假设各场比赛结果互不影响,且每场比赛必须分出胜负.
(1)若初赛后,甲、乙、丙、丁四队分别排在第七、八、九、十名,丁队与甲、乙、丙队比赛获胜的概率分别是0.4,0.5,0.6,甲队与乙队比赛获胜的概率是0.6,则丁队进入复赛的概率是多少?
(2)若甲,乙两队进入复赛,在复赛中,甲队与乙队需进行一场五局三胜制的比赛,只要其中一方获胜三局,比赛结束、假设各局比赛结果互不影响.若乙队每局比赛获胜的概率为,设比赛结束时乙队获胜的局数为X,求X的概率分布列与均值.
【解答】解:(1)依题意,记丁队进入复赛的事件为A,丁队进入复赛需参加两场比赛,第一场战胜丙队,记为事件A1,
第二场战胜甲乙比赛中的败者,记为事件A2,甲队战胜乙队记为事件B,
则P(A1)=0.6,P(B)=0.6,P()=0.4,,
因此0.6×0.5+0.4×0.4=0.46,
所以P(A)=P(A1)P(A2)=0.6×0.46=0.276.
(2)依题意,X的可能值为0,1,2,3,
,,
,,
所以X的概率分布列为:
X 0 1 2 3
P
数学期望为.
21.(12分)设点F为抛物线C:x2=2py(p>0)的焦点,过点F且斜率为的直线与C交于A,B两点(O为坐标原点).
(1)求抛物线C的方程;
(2)过点E(0,2)作两条斜率分别为k1,k2的直线l1,l2,它们分别与抛物线C交于点P,Q和R,S.已知|EP| |EQ|=|ER| |ES|,问:是否存在实数λ,使得k1+λk2为定值?若存在,求λ的值,若不存在,请说明理由.
【解答】解:(1)抛物线C:x2=2py(p>0)的焦点为F(0,),
直线AB的方程yx,
由,得x2﹣2py﹣p2=0,
设A(x1,y1),B(x2,y2),
所以x1+x2=2p,x1x2=﹣p2,
所以|x1﹣x2|2p,
所以S△AOB|OF||x1﹣x2|2p=2,p>0,
所以p=2,
所以抛物线C的方程为x2=4y.
(2)存在λ=1,使得k1+λk2为定值,
由题意可得直线l1的方程y=k1x+2,直线l2的方程为y=k2x+2,
联立,得x2﹣4k1x﹣8=0,
设P(x3,y3),Q(x4,y4),
所以x3+x4=4k1,x3x4=﹣8,
|EP||x3|,|EQ||x4|,
所以|EP| |EQ|=8(1),
设R(x5,y5),S(x6,y6),
同理可得x5+x6=4k2,x5x6=﹣8,
所以|ER| |ES|=8(1),
由|EP| |EQ|=|ER| |ES|,得8(1)=8(1),
即,而k1≠k2,
所以k1+k2=0,
所以存在λ=1,使得k1+λk2为定值0.
22.(12分)已知函数f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m.
(1)当m=0时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)若f(x)在[0,1]上存在两个零点x1,x2,证明:.
【解答】解:(1)已知f(x)=sinπx﹣3(x﹣1)ln(x+1)﹣m,函数定义域为(﹣1,+∞),
当m=0时,f(x)=sinπx﹣3(x﹣1)ln(x+1),
可得,
此时f′(0)=π+3,
又f(0)=0,
所以f(x)在x=0处的切线方程为y﹣0=(π+3)(x﹣0),
即y=(π+3)x;
(2)证明:不妨设g(x)=sinπx﹣3(x﹣1)ln(x+1),函数定义域为(﹣1,+∞),
若f(x)在[0,1]上存在两个零点x1,x2,
此时g(x)=m在[0,1]上存在两个零点x1,x2,
可得,
不妨设h(x)=g′(x),
可得h′(x)=﹣π2sinπxπ2sinπx,
易知对任意的x∈[0,1],都有sinπx>0,
所以对任意的x∈[0,1],h′(x)<0恒成立,
则g′(x)在[0,1]上单调递减,
又g′(0)=π+3,g′(1)=﹣π﹣3ln2<0,
所以存在x0∈(0,1),使得g′(x0)=0,
当0≤x<x0时,g′(x)>0,g(x)单调递增;
当x0<x≤1时,g′(x)<0,g(x)单调递减,
所以当x=x0时,函数g(x)取到极大值,极大值g(x0)=sinπx0﹣3(x0﹣1)ln(x0+1)>0,
又g(0)=g(1)=0,
所以当且仅当0≤m<sinπx0﹣3(x0﹣1)ln(x0+1)时,
g(x)=m在[0,x0)和(x0,1]上各恰有一个零点,分别为x1,x2,
不妨设x1<x2,
由(1)知,g(x)在x=0处的切线方程为y=(π+3)x,
不妨设k(x)=g(x)﹣(π+3)x,
可得k′(x)=g′(x)﹣(π+3)=h(x)﹣(π+3),
不妨设m(x)=k′(x),
可得m′(x)=h′(x)<0,
所以m(x)在[0,1]上单调递减,
即k(x)在[0,1]上单调递减,
又k′(0)=g′(0)﹣(π+3)=0,
所以对任意x∈[0,1],都有k′(x)≤0,
则k(x)在[0,1]上单调递减,
又k(0)=g(0)=0,
所以对任意的x∈[0,1],都有k(x)≤0,
则当x∈[0,1]时,g(x)≤(π+3)x;
同理得,g(x)在x=1处的切线方程为y=(π+3ln2)(1﹣x),
不妨设n(x)=g(x)﹣(π+3ln2)(1﹣x),
可得n′(x)=g′(x)+(π+3ln2)=h(x)+(π+3ln2),
不妨设p(x)=n′(x),
可得p′(x)=h′(x)<0,
所以n′(x)在[0,1]单调递减,
又n′(1)=g′(1)+(π+3ln2)=0,
所以对任意x∈[0,1],都有n′(x)≥0,
则n(x)在[0,1]上单调递增,
又n(1)=g(1)=0,
所以对任意x∈[0,1],都有n(x)≤0,
则当x∈[0,1]时,g(x)≤(π+3ln2)(1﹣x),
不妨设(π+3)x=m和(π+3ln2)(1﹣x)=m的零点分别为,,
因为(π+3)x3=m=g(x1)≤(π+3)x1,
所以x3≤x1,
因为(π+3ln2)(1﹣x4)=m=g(x2)≤(π+3ln2)(1﹣x2),
所以x4≥x2,
则x3≤x1<x2≤x4,
故|x1﹣x2|≤x4﹣x3=11.
第1页(共1页)
同课章节目录
