人教版八年级数学上册试题 12.1 全等三角形(含解析)
文档属性
| 名称 | 人教版八年级数学上册试题 12.1 全等三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 810.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 13:18:42 | ||
图片预览


文档简介
12.1 全等三角形
一、单选题
1.下列各组图形中,不是全等图形的是( )
A. B. C. D.
2.如图为6个边长相等的正方形的组合图形,则∠1+∠3-∠2=( )
A.30° B.45° C.60° D.135°
3.如图,,点在上,与相交于点,,则的度数为( )
A. B. C. D.
4.如图,点、、在同一直线上,若,,,则等于( )
A.7 B.8 C.9 D.10
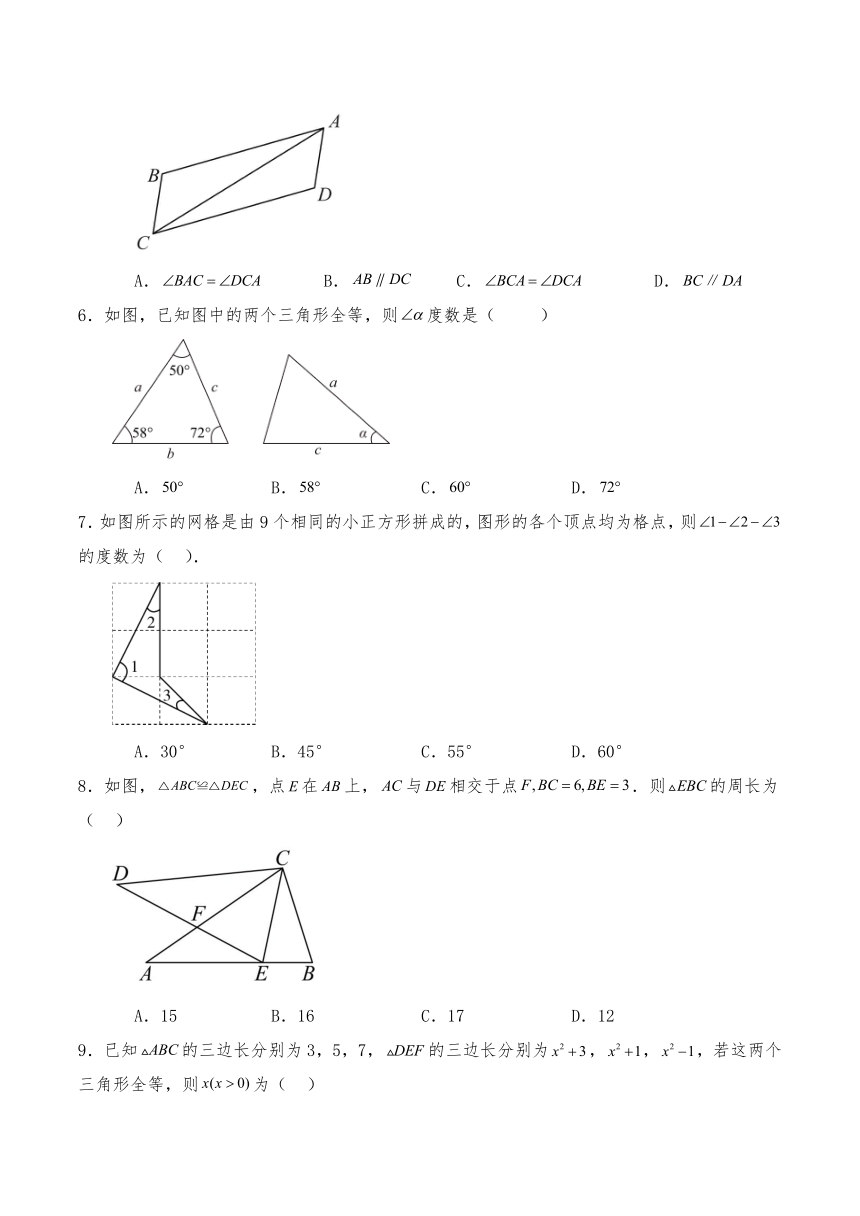
5.如图,, 与,与是对应边,则下列结论错误的是( )
A. B. C. D.
6.如图,已知图中的两个三角形全等,则度数是( )
A. B. C. D.
7.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
8.如图,,点在上,与相交于点.则的周长为( )
A.15 B.16 C.17 D.12
9.已知的三边长分别为3,5,7,的三边长分别为,,,若这两个三角形全等,则为( )
A.2 B. C.3 D.4
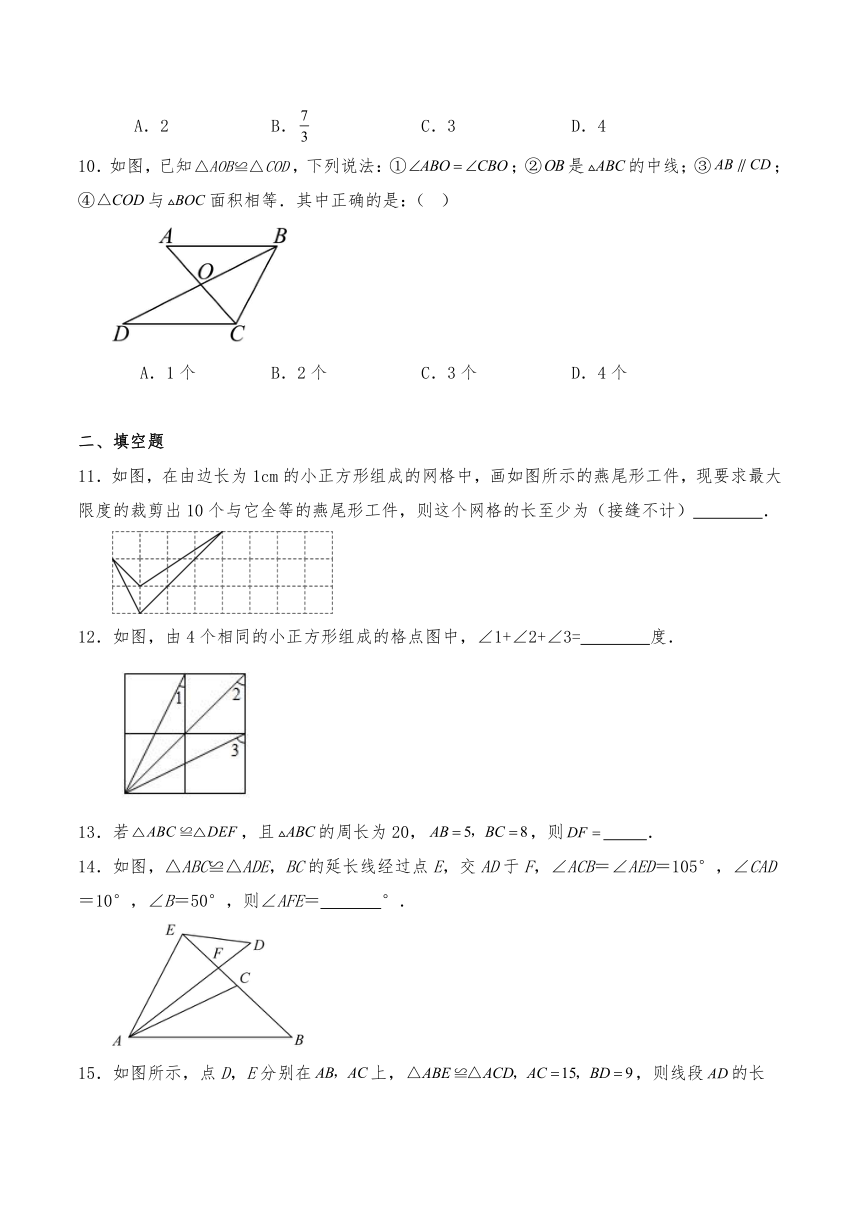
10.如图,已知,下列说法:①;②是的中线;③;④与面积相等.其中正确的是:( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计) .
12.如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3= 度.
13.若,且的周长为20,,则 .
14.如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠AFE= °.
15.如图所示,点D,E分别在上,,则线段的长是 .
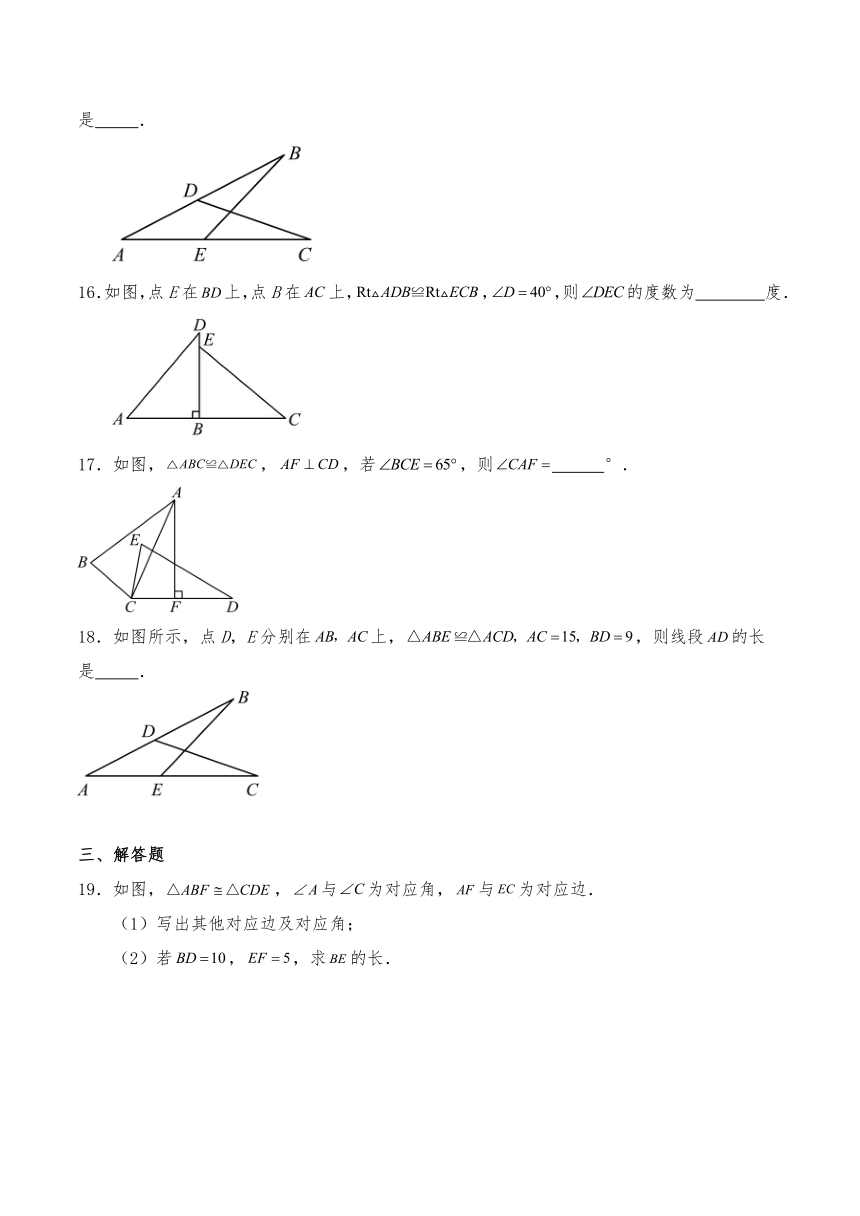
16.如图,点E在上,点B在上,,,则的度数为 度.
17.如图,,,若,则 °.
18.如图所示,点D,E分别在上,,则线段的长是 .
三、解答题
19.如图,,与为对应角,与为对应边.
(1)写出其他对应边及对应角;
(2)若,,求的长.
20.如图,已知,点E在上,与交于点F.
(1)若,,求的长;
(2)若,,求的度数.
21.如图,已知,点D在的延长线上,点E在上,连接并延长交于点F.
(1)求证:.
(2)若点F为线段的中点,的面积为10,的面积为6,则四边形的面积为______.
22.(1)如图,求x的值.
(2)如图所示,已知.如果,求的长.
23.如图所示,在正方形中,E是边上的一点,F是延长线上的一点.已知,试探究线段与之间的关系,并说明理由.
24.如图所示,E为线段上一点,.
(1)试猜想线段与满足什么条件时,能保证,并证明你的结论;
(2)猜想的数量关系.
答案:
一、单选题
1.A
【分析】本题考查的是全等形的识别.根据能够完全重合的两个图形是全等图形对各选项分析即可得解.
解:观察发现,B、C、D选项的两个图形都可以完全重合,
∴B、C、D选项的两个图形都是全等图形,
A选项中两个图形不可能完全重合,
∴它们不是全等形.
故选:A.
2.B
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠3-∠2.
解:
∵在△ABC和△DBE中
,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∵∠2=45°
∴∠1+∠3-∠2=90°-45°=45°,
故选B.
3.A
【分析】本题考查了三角形全等的判定及平角的定义.由,得,,即是等腰三角形,由可得,故,最后根据平角的性质即可得的度数.
解:,
,,
,
,
,
.
故选:A.
4.C
【分析】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.
由全等三角形的性质推出,,求出,即可得到的长.
解:,
,,
,
,
.
故选:C.
5.C
【分析】本题主要考查了全等三角形的性质,平行线的判定,根据全等三角形对应角相等得到,进而得到,据此可得答案.
解:∵,
∴,
∴,
根据现有条件无法证明,
故选:C.
6.A
【分析】本题考查了全等三角形的性质,正确得出对应角是解题的关键.根据全等三角形对应角相等即可得出结论.
解:∵图中的两个三角形全等,
∴,
故选:A.
7.B
【分析】根据网格特点,可得出,,,进而可求解.
解:如图,则,,,
∴,
故选:B.
8.A
【分析】本题考查了全等三角形的性质,根据得到,根据周长为,选择即可.
解:∵,,
∴,
∴,
故选A.
9.A
【分析】本题主要考查了全等三角形的知识.根据全等三角形的性质可得:与3是对应边,与5是对应边,与7是对应边,由此即可得出正确选项.
解:∵与全等,
与3是对应边,与5是对应边,与7是对应边,
,
,
.
故选:A.
10.C
【分析】本题主要考查全等三角形的性质,根据,可知,,,.
解:①∵,
∴.
说法①错误.
②∵,
∴.
∴是的中线.
说法②正确.
③∵,
∴.
∴.
说法③正确.
④∵,
∴,且的边上的高与的边上的高相等.
∴与面积相等.
说法④正确.
综上所述,说法正确的有②③④,共3个.
故选:C
二、填空题
11.21cm
【分析】根据题意,画出图形,找出相应的规律进行计算即可.
解:如图,
∵后面画出的图形与第一个图形完全一样
∴画第二个图形的时候,需往右走1cm,画第三个图的时候,需要再往右走3cm,画第四个图的时候,需要再往右走1cm…,
∴画第10个图时,网格的长至少为(cm).
故答案为:21cm
12.135
【分析】首先利用全等三角形的判定和性质求出的值,即可得出答案;
解:如图所示,
在△ACB和△DCE中,
,
∴,
∴,
∴;
故答案是:.
13.7
【分析】此题考查了全等三角形的性质,先根据周长和已知边长求出的长,再根据全等三角形对应边相等即可得到答案.
解:∵的周长为20,,
∴,
∵,
∴,
答案为:7
14.85
【分析】利用三角形内角和定理求出∠BAC=25°,再根据三角形外角的性质可得答案.
解:在△ABC中,∵∠B=50°,∠ACB=105°,
∴∠BAC=25°,
∵∠CAD=10°,∠B=50°,
∴∠AFE=∠BAD+∠B=∠BAC+∠CAD+∠B=25°+10°+50°=85°,
故答案为:85.
15.6
【分析】本题考查了全等三角形的性质,根据,可得,即可得到的长,熟记全等三角形的对应边相等,对应角相等是解题的关键.
解:,
,
,
故答案为:6.
16.130
【分析】本题主要考查了全等三角形的性质,三角形的外角的性质.根据全等三角形的性质,可得,,从而得到,再由三角形的外角的性质,即可求解.
解:∵,
∴,,
∵,
∴,
∴.
故答案为:130
17.
【分析】本题主要考查了全等三角形的性质,直角三角形的性质,解题的关键是掌握全等三角形的性质.由可得,推出,最后根据直角三角形的性质即可求解.
解:,
,
,
即,
,
,
,
故答案为:.
18.6
【分析】本题考查了全等三角形的性质,根据,可得,即可得到的长,熟记全等三角形的对应边相等,对应角相等是解题的关键.
【详解】解:,
,
,
故答案为:6.
三、解答题
19.
(1)解:其他对应边:和,和;对应角:和,和;
(2)∵,
∴,
∴,即
∵,
∴,
∴
20.
解:(1)(1)∵,,
∴,
∴.
(2)∵,
∴.
∵,,
∴,
∴,
∴.
21.
解:(1)证明:∵△ACD≌△BCE,
∴,
∵,点D在BC的延长线上,
∴,
∵,
∴,
∴,即;
(2)∵点F为线段的中点,,
∴,
∵△ACD≌△BCE,
∴,
∴四边形的面积,
故答案为:.
22.
解:(1)由三角形的外角性质可知,,
解得,.
(2),
,
,
∴,
,
.
23.
解:,且,理由如下:
如图所示,延长交于点.
,
,.
在中,,
.
,
即,
∴,且.
24.
(1)解:.理由如下:
设,则,
∴.
,
,
,
,
.
(2)解:.理由如下:
,
,,
,
.
一、单选题
1.下列各组图形中,不是全等图形的是( )
A. B. C. D.
2.如图为6个边长相等的正方形的组合图形,则∠1+∠3-∠2=( )
A.30° B.45° C.60° D.135°
3.如图,,点在上,与相交于点,,则的度数为( )
A. B. C. D.
4.如图,点、、在同一直线上,若,,,则等于( )
A.7 B.8 C.9 D.10
5.如图,, 与,与是对应边,则下列结论错误的是( )
A. B. C. D.
6.如图,已知图中的两个三角形全等,则度数是( )
A. B. C. D.
7.如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则的度数为( ).
A.30° B.45° C.55° D.60°
8.如图,,点在上,与相交于点.则的周长为( )
A.15 B.16 C.17 D.12
9.已知的三边长分别为3,5,7,的三边长分别为,,,若这两个三角形全等,则为( )
A.2 B. C.3 D.4
10.如图,已知,下列说法:①;②是的中线;③;④与面积相等.其中正确的是:( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计) .
12.如图,由4个相同的小正方形组成的格点图中,∠1+∠2+∠3= 度.
13.若,且的周长为20,,则 .
14.如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠AFE= °.
15.如图所示,点D,E分别在上,,则线段的长是 .
16.如图,点E在上,点B在上,,,则的度数为 度.
17.如图,,,若,则 °.
18.如图所示,点D,E分别在上,,则线段的长是 .
三、解答题
19.如图,,与为对应角,与为对应边.
(1)写出其他对应边及对应角;
(2)若,,求的长.
20.如图,已知,点E在上,与交于点F.
(1)若,,求的长;
(2)若,,求的度数.
21.如图,已知,点D在的延长线上,点E在上,连接并延长交于点F.
(1)求证:.
(2)若点F为线段的中点,的面积为10,的面积为6,则四边形的面积为______.
22.(1)如图,求x的值.
(2)如图所示,已知.如果,求的长.
23.如图所示,在正方形中,E是边上的一点,F是延长线上的一点.已知,试探究线段与之间的关系,并说明理由.
24.如图所示,E为线段上一点,.
(1)试猜想线段与满足什么条件时,能保证,并证明你的结论;
(2)猜想的数量关系.
答案:
一、单选题
1.A
【分析】本题考查的是全等形的识别.根据能够完全重合的两个图形是全等图形对各选项分析即可得解.
解:观察发现,B、C、D选项的两个图形都可以完全重合,
∴B、C、D选项的两个图形都是全等图形,
A选项中两个图形不可能完全重合,
∴它们不是全等形.
故选:A.
2.B
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=∠1+∠3=90°,可得∠1+∠3-∠2.
解:
∵在△ABC和△DBE中
,
∴△ABC≌△DBE(SAS),
∴∠3=∠ACB,
∵∠ACB+∠1=90°,
∴∠1+∠3=90°,
∵∠2=45°
∴∠1+∠3-∠2=90°-45°=45°,
故选B.
3.A
【分析】本题考查了三角形全等的判定及平角的定义.由,得,,即是等腰三角形,由可得,故,最后根据平角的性质即可得的度数.
解:,
,,
,
,
,
.
故选:A.
4.C
【分析】本题考查全等三角形的性质,关键是掌握全等三角形的对应边相等.
由全等三角形的性质推出,,求出,即可得到的长.
解:,
,,
,
,
.
故选:C.
5.C
【分析】本题主要考查了全等三角形的性质,平行线的判定,根据全等三角形对应角相等得到,进而得到,据此可得答案.
解:∵,
∴,
∴,
根据现有条件无法证明,
故选:C.
6.A
【分析】本题考查了全等三角形的性质,正确得出对应角是解题的关键.根据全等三角形对应角相等即可得出结论.
解:∵图中的两个三角形全等,
∴,
故选:A.
7.B
【分析】根据网格特点,可得出,,,进而可求解.
解:如图,则,,,
∴,
故选:B.
8.A
【分析】本题考查了全等三角形的性质,根据得到,根据周长为,选择即可.
解:∵,,
∴,
∴,
故选A.
9.A
【分析】本题主要考查了全等三角形的知识.根据全等三角形的性质可得:与3是对应边,与5是对应边,与7是对应边,由此即可得出正确选项.
解:∵与全等,
与3是对应边,与5是对应边,与7是对应边,
,
,
.
故选:A.
10.C
【分析】本题主要考查全等三角形的性质,根据,可知,,,.
解:①∵,
∴.
说法①错误.
②∵,
∴.
∴是的中线.
说法②正确.
③∵,
∴.
∴.
说法③正确.
④∵,
∴,且的边上的高与的边上的高相等.
∴与面积相等.
说法④正确.
综上所述,说法正确的有②③④,共3个.
故选:C
二、填空题
11.21cm
【分析】根据题意,画出图形,找出相应的规律进行计算即可.
解:如图,
∵后面画出的图形与第一个图形完全一样
∴画第二个图形的时候,需往右走1cm,画第三个图的时候,需要再往右走3cm,画第四个图的时候,需要再往右走1cm…,
∴画第10个图时,网格的长至少为(cm).
故答案为:21cm
12.135
【分析】首先利用全等三角形的判定和性质求出的值,即可得出答案;
解:如图所示,
在△ACB和△DCE中,
,
∴,
∴,
∴;
故答案是:.
13.7
【分析】此题考查了全等三角形的性质,先根据周长和已知边长求出的长,再根据全等三角形对应边相等即可得到答案.
解:∵的周长为20,,
∴,
∵,
∴,
答案为:7
14.85
【分析】利用三角形内角和定理求出∠BAC=25°,再根据三角形外角的性质可得答案.
解:在△ABC中,∵∠B=50°,∠ACB=105°,
∴∠BAC=25°,
∵∠CAD=10°,∠B=50°,
∴∠AFE=∠BAD+∠B=∠BAC+∠CAD+∠B=25°+10°+50°=85°,
故答案为:85.
15.6
【分析】本题考查了全等三角形的性质,根据,可得,即可得到的长,熟记全等三角形的对应边相等,对应角相等是解题的关键.
解:,
,
,
故答案为:6.
16.130
【分析】本题主要考查了全等三角形的性质,三角形的外角的性质.根据全等三角形的性质,可得,,从而得到,再由三角形的外角的性质,即可求解.
解:∵,
∴,,
∵,
∴,
∴.
故答案为:130
17.
【分析】本题主要考查了全等三角形的性质,直角三角形的性质,解题的关键是掌握全等三角形的性质.由可得,推出,最后根据直角三角形的性质即可求解.
解:,
,
,
即,
,
,
,
故答案为:.
18.6
【分析】本题考查了全等三角形的性质,根据,可得,即可得到的长,熟记全等三角形的对应边相等,对应角相等是解题的关键.
【详解】解:,
,
,
故答案为:6.
三、解答题
19.
(1)解:其他对应边:和,和;对应角:和,和;
(2)∵,
∴,
∴,即
∵,
∴,
∴
20.
解:(1)(1)∵,,
∴,
∴.
(2)∵,
∴.
∵,,
∴,
∴,
∴.
21.
解:(1)证明:∵△ACD≌△BCE,
∴,
∵,点D在BC的延长线上,
∴,
∵,
∴,
∴,即;
(2)∵点F为线段的中点,,
∴,
∵△ACD≌△BCE,
∴,
∴四边形的面积,
故答案为:.
22.
解:(1)由三角形的外角性质可知,,
解得,.
(2),
,
,
∴,
,
.
23.
解:,且,理由如下:
如图所示,延长交于点.
,
,.
在中,,
.
,
即,
∴,且.
24.
(1)解:.理由如下:
设,则,
∴.
,
,
,
,
.
(2)解:.理由如下:
,
,,
,
.
