专题8 有关中点的证明与计算 课件(共17张PPT)
文档属性
| 名称 | 专题8 有关中点的证明与计算 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 06:09:46 | ||
图片预览

文档简介
(共17张PPT)
专题8 有关中点的证明与计算
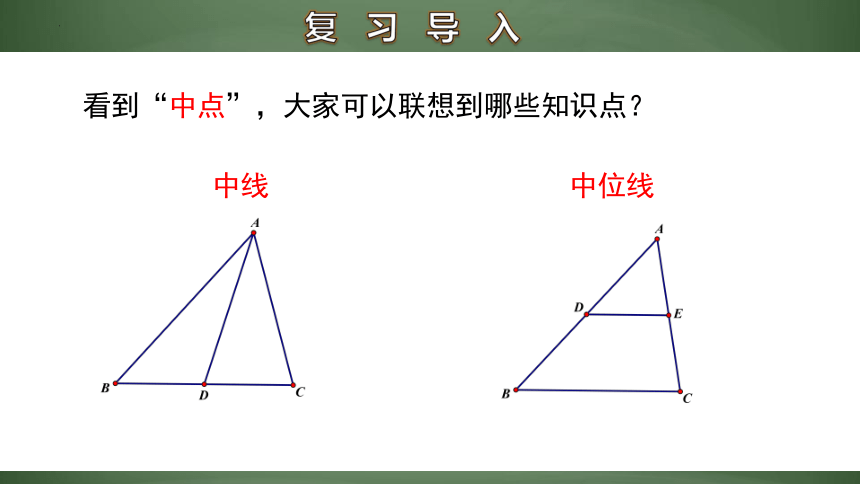
复 习 导 入
看到“中点”,大家可以联想到哪些知识点?
中线
中位线
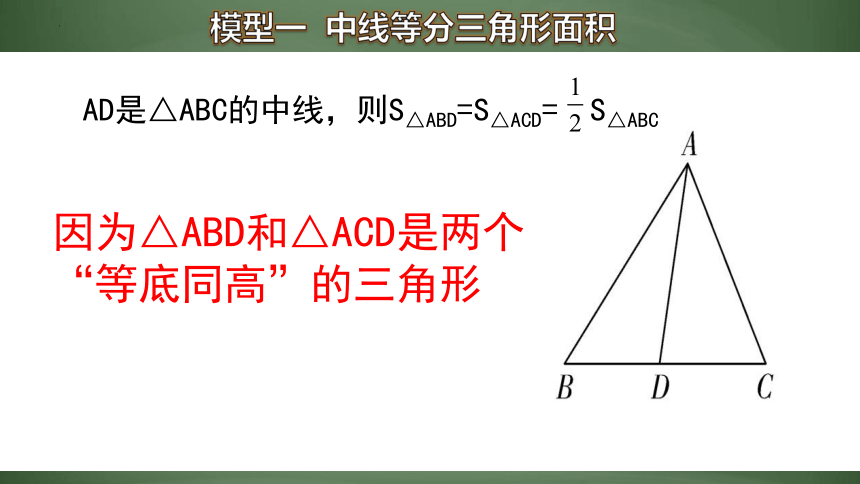
模型一 中线等分三角形面积
AD是△ABC的中线,则S△ABD=S△ACD= S△ABC
因为△ABD和△ACD是两个“等底同高”的三角形
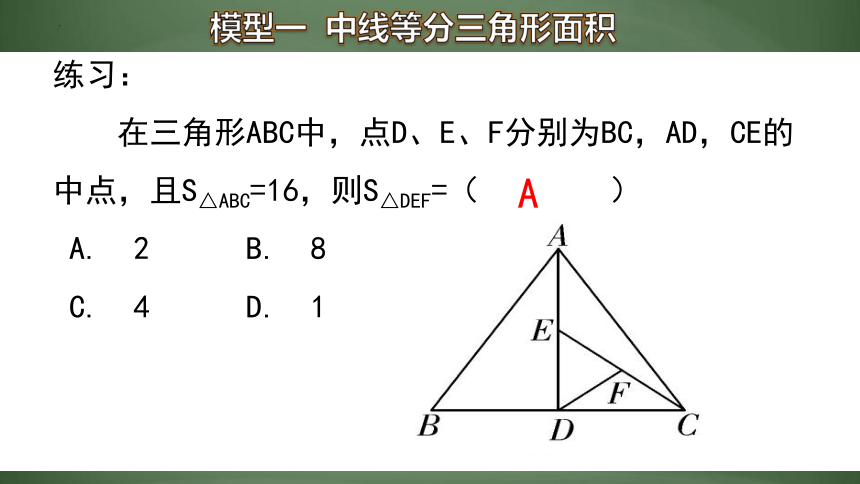
练习:
在三角形ABC中,点D、E、F分别为BC,AD,CE的中点,且S△ABC=16,则S△DEF=( )
A. 2 B. 8
C. 4 D. 1
模型一 中线等分三角形面积
A
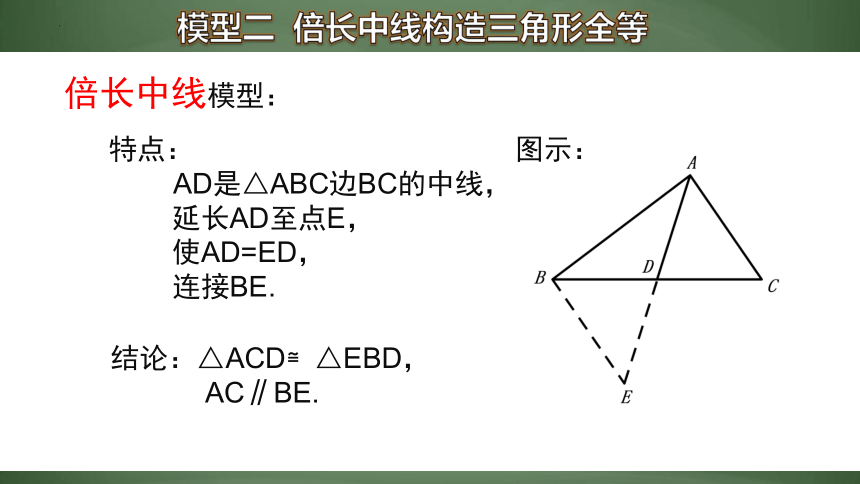
倍长中线模型:
特点:
AD是△ABC边BC的中线,
延长AD至点E,
使AD=ED,
连接BE.
结论:△ACD≌△EBD,
AC∥BE.
图示:
模型二 倍长中线构造三角形全等
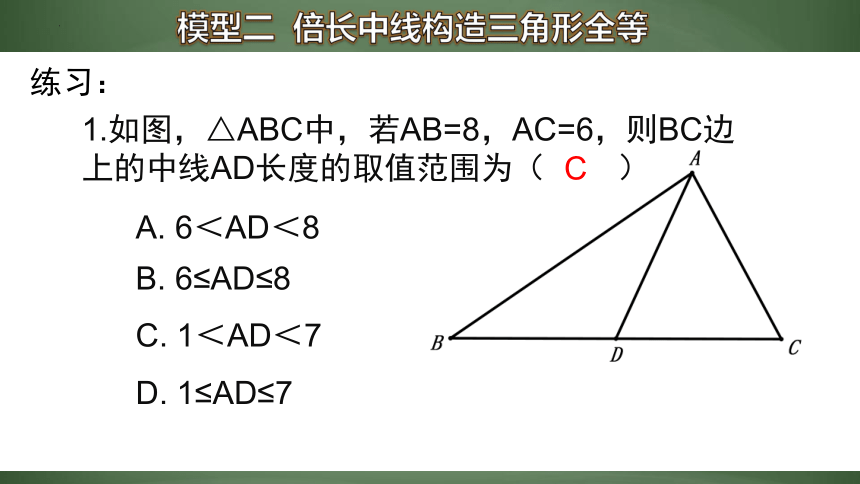
模型二 倍长中线构造三角形全等
1.如图,△ABC中,若AB=8,AC=6,则BC边上的中线AD长度的取值范围为( )
A. 6<AD<8
B. 6≤AD≤8
C. 1<AD<7
D. 1≤AD≤7
C
练习:
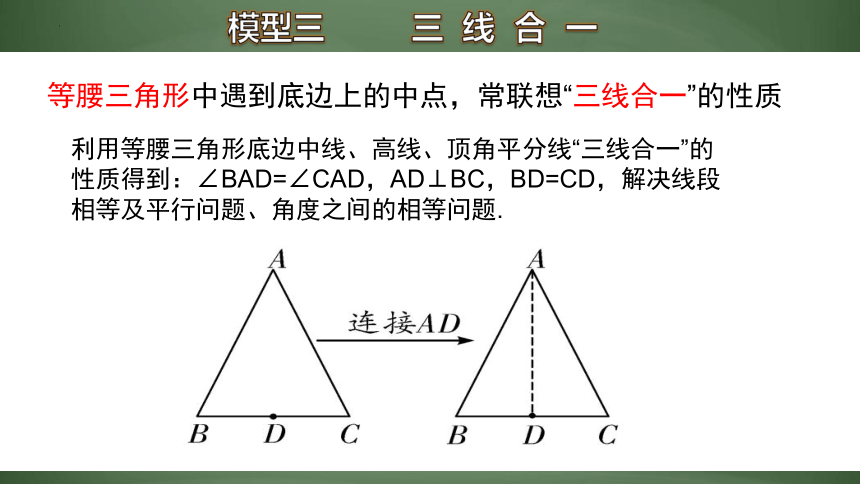
模型三 三 线 合 一
等腰三角形中遇到底边上的中点,常联想“三线合一”的性质
利用等腰三角形底边中线、高线、顶角平分线“三线合一”的性质得到:∠BAD=∠CAD,AD⊥BC,BD=CD,解决线段相等及平行问题、角度之间的相等问题.
模型三 三 线 合 一
练习:
如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°.
求∠EDC的度数.
证明:∵在△ABC中,AB=AC,
点D为BC的中点,
∴∠ADB=∠ADC=90°.
∵AE=AD,
∴∠ADE=∠AED=75°,
则∠EDC=∠ADC-∠ADE
=90°-75°
=15°.
模型四 斜 中 半
直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”.
利用“斜边上的中线等于斜边的一半”可CD=AD=BD=1/2AB来解题,有时有直角无中点,要找中点.常用:证明线段相等或求线段长;构造角相等进行等量代换.
证明:∵AD⊥DB,点E为AB的中点,
∴DE=BE=1/2AB,
∴∠ABD=∠BDE.
∵DE∥BC,
∴∠CBD=∠BDE,
∴∠ABD=∠CBD.
所以BD平分∠ABC.
模型四 斜 中 半
如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
求证:BD平分∠ABC.
练习:
模型五 构造三角形中位线
多个中点出现或平行+中点,常联想“ 构造三角形中位线”.
利用三角形中位线的性质定理:DE∥BC,且DE=1/2BC,△ADE∽△ABC,解决线段之间的相等或比例关系及平行问题.
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE,若∠ABC=60°,∠BAC=80°,则∠1的度数为( ).
A. 50° B. 40°
C. 30° D. 20°
练习:
模型五 构造三角形中位线
B
模型六 垂直平分线的性质
三角形一边垂线过这边中点,常联想“ 垂直平分线的性质”.
利用垂直平分线的性质等到:BE=CE,证明线段间的数量关系.
如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.
求证:DC=BE.
练习:
证明:连接DE,
∵G是CE的中点,DG⊥CE,,
∴DG是CE的垂直平分线,
∴DE=DC.
∵△ABC中,AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE=1/2AB,
∴DC=BE.
模型六 垂直平分线的性质
课 堂 小 结
谈谈你本节课的收获.
作 业 布 置
见精准作业单.
专题8 有关中点的证明与计算
复 习 导 入
看到“中点”,大家可以联想到哪些知识点?
中线
中位线
模型一 中线等分三角形面积
AD是△ABC的中线,则S△ABD=S△ACD= S△ABC
因为△ABD和△ACD是两个“等底同高”的三角形
练习:
在三角形ABC中,点D、E、F分别为BC,AD,CE的中点,且S△ABC=16,则S△DEF=( )
A. 2 B. 8
C. 4 D. 1
模型一 中线等分三角形面积
A
倍长中线模型:
特点:
AD是△ABC边BC的中线,
延长AD至点E,
使AD=ED,
连接BE.
结论:△ACD≌△EBD,
AC∥BE.
图示:
模型二 倍长中线构造三角形全等
模型二 倍长中线构造三角形全等
1.如图,△ABC中,若AB=8,AC=6,则BC边上的中线AD长度的取值范围为( )
A. 6<AD<8
B. 6≤AD≤8
C. 1<AD<7
D. 1≤AD≤7
C
练习:
模型三 三 线 合 一
等腰三角形中遇到底边上的中点,常联想“三线合一”的性质
利用等腰三角形底边中线、高线、顶角平分线“三线合一”的性质得到:∠BAD=∠CAD,AD⊥BC,BD=CD,解决线段相等及平行问题、角度之间的相等问题.
模型三 三 线 合 一
练习:
如图,△ABC中,AB=AC,点D是BC的中点,E是AC上一点,且AE=AD,若∠AED=75°.
求∠EDC的度数.
证明:∵在△ABC中,AB=AC,
点D为BC的中点,
∴∠ADB=∠ADC=90°.
∵AE=AD,
∴∠ADE=∠AED=75°,
则∠EDC=∠ADC-∠ADE
=90°-75°
=15°.
模型四 斜 中 半
直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”.
利用“斜边上的中线等于斜边的一半”可CD=AD=BD=1/2AB来解题,有时有直角无中点,要找中点.常用:证明线段相等或求线段长;构造角相等进行等量代换.
证明:∵AD⊥DB,点E为AB的中点,
∴DE=BE=1/2AB,
∴∠ABD=∠BDE.
∵DE∥BC,
∴∠CBD=∠BDE,
∴∠ABD=∠CBD.
所以BD平分∠ABC.
模型四 斜 中 半
如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
求证:BD平分∠ABC.
练习:
模型五 构造三角形中位线
多个中点出现或平行+中点,常联想“ 构造三角形中位线”.
利用三角形中位线的性质定理:DE∥BC,且DE=1/2BC,△ADE∽△ABC,解决线段之间的相等或比例关系及平行问题.
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE,若∠ABC=60°,∠BAC=80°,则∠1的度数为( ).
A. 50° B. 40°
C. 30° D. 20°
练习:
模型五 构造三角形中位线
B
模型六 垂直平分线的性质
三角形一边垂线过这边中点,常联想“ 垂直平分线的性质”.
利用垂直平分线的性质等到:BE=CE,证明线段间的数量关系.
如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.
求证:DC=BE.
练习:
证明:连接DE,
∵G是CE的中点,DG⊥CE,,
∴DG是CE的垂直平分线,
∴DE=DC.
∵△ABC中,AD是高,CE是中线,
∴DE是Rt△ADB的斜边AB上的中线,
∴DE=BE=1/2AB,
∴DC=BE.
模型六 垂直平分线的性质
课 堂 小 结
谈谈你本节课的收获.
作 业 布 置
见精准作业单.
