18.1.1平行四边形的边、角的特征(第1课时)课件(共15张PPT)2023-2024学年人教版八年级数学下学期
文档属性
| 名称 | 18.1.1平行四边形的边、角的特征(第1课时)课件(共15张PPT)2023-2024学年人教版八年级数学下学期 |

|
|
| 格式 | pptx | ||
| 文件大小 | 36.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第 1 课时 | 平行四边形的边、角的特征
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
问题1 观察这些图片,它们是否都有平行四边形的形象?
环节一:观察抽象 形成概念
你还记得平行四边形的定义吗?
请按下暂停键,30秒后再继续学行四边形定义:
两组对边分别平行的四边形叫做平行四边形.
性质:∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
判定:∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义).
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
ABCD
符号表示
A
B
C
D
平行四边形ABCD
记作:
平行四边形的定义:既是判定又是性质
认识平行四边形的基本元素
边 对边:AB与CD;AD与BC
邻边:如:AB与AD;AB与BC;
AD与DC;DC与BC
角 对角:∠ADC与∠ABC;∠BCD与∠BAD
邻角:如∠ABC与∠DAB;∠BCD与∠ADC等
对角线 AC,BD
问题4 对于平行四边形,从定义出发,你能得出它的性质吗?
你能证明这些结论吗?
环节二:概括证明 探究性质
给出图形定义→研究图形性质→探索图形判定条件.
问题3 回忆我们的学习经历,研究几何图形的一般思路是什么?
猜想:平行四边形对角相等,
平行四边形对边相等.
请按下暂停键,2分钟后再继续学习
提示(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全等的三角形.
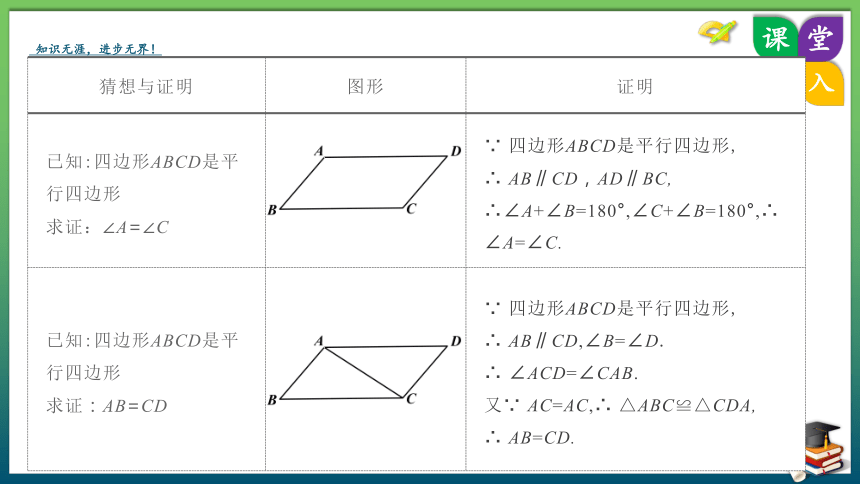
猜想与证明 图形 证明
已知:四边形ABCD是平行四边形 求证:∠A=∠C ∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC,
∴∠A+∠B=180°,∠C+∠B=180°,∴ ∠A=∠C.
已知:四边形ABCD是平行四边形 求证:AB=CD ∵ 四边形ABCD是平行四边形,
∴ AB∥CD,∠B=∠D.
∴ ∠ACD=∠CAB.
又∵ AC=AC,∴ △ABC≌△CDA,
∴ AB=CD.
平行四边形的性质定理:
平行四边形的对边相等,
平行四边形的对角相等.
∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD , AD=BC(平行四边形的性质);
∴ ∠A=∠C, ∠B=∠D(平行四边形的性质).
环节二:概括证明 探究性质
环节三:应用知识 解决问题
问题1 如图,在 ABCD中,∠B=40°,求其余三个角的度数.
问题2 如图,在 ABCD中,AD=8,其周长为24,求其余三条边的长度.
请按下暂停键,2分钟后再继续学习
答案:由平行四边形的对角相等,可知∠D=∠B=40°,由平行四边形的对边平行,从而同旁内角互补,可知∠A=∠C=140°.
答案:由平行四边形的对边相等,可知BC=AD=8, AB=CD,由周长为24,可知,AD+AB=12,从而AB=4,可知CD=4.
追问:DE=BF 吗
环节三:应用知识 解决问题
例1 如图, ABCD中, DE⊥AB, BF⊥CD, 垂足分别为E,F.
求证:AE=CF.
A
B
C
D
E
F
请按下暂停键,2分钟后再继续学习
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,∠A=∠C.
∵ DE⊥AB,BF⊥CD,
∴ ∠AED=∠BFC=90°.
∴ △ADE≌△CBF,
∴ AE=CF.
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?为什么?
平行线间的距离
环节三:应用知识 解决问题
定义 两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线之间的距离
数学语言表示 直线a∥b,D为直线b上的任意一点,AD⊥a,垂足为A,线段AD的长就是a,b之间的距离
性质 (1)两条平行线之间的距离处处相等;
(2)两条平行线之间的任何两条平行线段都是相等的(需证明)
两点之间的距离 连接两点之间的线段的长度
点到直线的距离 点到直线的垂线段的长度
两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离
概念辨析
例3 △ABC是等腰三角形, AB=AC, P是底边BC上一动点, PE∥AB, PF∥AC, 点E,F分别在AC, AB上.求证:PE+PF=AB.
A
B
C
E
F
P
环节三:应用知识 解决问题
请按下暂停键,3分钟后再继续学习
证明:∵ PE∥AB , PF∥AC,
∴ 四边形AFPE是平行四边形,
∴ AF=PE,AE=PF,
∵ AB=AC,∴ ∠B=∠C.
∵ PF∥AC,∴ ∠FPB=∠C,
∴ ∠B=∠FPB,∴ BF=PF.
∵ AB=AF+BF, ∴ PE+PF=AB.
(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你认
为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?你
认为接下来可以研究什么问题?
课堂小结
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
第 1 课时 | 平行四边形的边、角的特征
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
问题1 观察这些图片,它们是否都有平行四边形的形象?
环节一:观察抽象 形成概念
你还记得平行四边形的定义吗?
请按下暂停键,30秒后再继续学行四边形定义:
两组对边分别平行的四边形叫做平行四边形.
性质:∵ 四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
判定:∵ AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义).
问题2 我们用符号“△”与三个顶点字母表示三角形;对于平行四边形,我们也有类似的表示方法吗?
ABCD
符号表示
A
B
C
D
平行四边形ABCD
记作:
平行四边形的定义:既是判定又是性质
认识平行四边形的基本元素
边 对边:AB与CD;AD与BC
邻边:如:AB与AD;AB与BC;
AD与DC;DC与BC
角 对角:∠ADC与∠ABC;∠BCD与∠BAD
邻角:如∠ABC与∠DAB;∠BCD与∠ADC等
对角线 AC,BD
问题4 对于平行四边形,从定义出发,你能得出它的性质吗?
你能证明这些结论吗?
环节二:概括证明 探究性质
给出图形定义→研究图形性质→探索图形判定条件.
问题3 回忆我们的学习经历,研究几何图形的一般思路是什么?
猜想:平行四边形对角相等,
平行四边形对边相等.
请按下暂停键,2分钟后再继续学习
提示(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全等的三角形.
猜想与证明 图形 证明
已知:四边形ABCD是平行四边形 求证:∠A=∠C ∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC,
∴∠A+∠B=180°,∠C+∠B=180°,∴ ∠A=∠C.
已知:四边形ABCD是平行四边形 求证:AB=CD ∵ 四边形ABCD是平行四边形,
∴ AB∥CD,∠B=∠D.
∴ ∠ACD=∠CAB.
又∵ AC=AC,∴ △ABC≌△CDA,
∴ AB=CD.
平行四边形的性质定理:
平行四边形的对边相等,
平行四边形的对角相等.
∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD , AD=BC(平行四边形的性质);
∴ ∠A=∠C, ∠B=∠D(平行四边形的性质).
环节二:概括证明 探究性质
环节三:应用知识 解决问题
问题1 如图,在 ABCD中,∠B=40°,求其余三个角的度数.
问题2 如图,在 ABCD中,AD=8,其周长为24,求其余三条边的长度.
请按下暂停键,2分钟后再继续学习
答案:由平行四边形的对角相等,可知∠D=∠B=40°,由平行四边形的对边平行,从而同旁内角互补,可知∠A=∠C=140°.
答案:由平行四边形的对边相等,可知BC=AD=8, AB=CD,由周长为24,可知,AD+AB=12,从而AB=4,可知CD=4.
追问:DE=BF 吗
环节三:应用知识 解决问题
例1 如图, ABCD中, DE⊥AB, BF⊥CD, 垂足分别为E,F.
求证:AE=CF.
A
B
C
D
E
F
请按下暂停键,2分钟后再继续学习
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,∠A=∠C.
∵ DE⊥AB,BF⊥CD,
∴ ∠AED=∠BFC=90°.
∴ △ADE≌△CBF,
∴ AE=CF.
例2 如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?为什么?
平行线间的距离
环节三:应用知识 解决问题
定义 两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线之间的距离
数学语言表示 直线a∥b,D为直线b上的任意一点,AD⊥a,垂足为A,线段AD的长就是a,b之间的距离
性质 (1)两条平行线之间的距离处处相等;
(2)两条平行线之间的任何两条平行线段都是相等的(需证明)
两点之间的距离 连接两点之间的线段的长度
点到直线的距离 点到直线的垂线段的长度
两条平行线之间的距离 两条平行线中,一条直线上任意一点到另一条直线的距离
概念辨析
例3 △ABC是等腰三角形, AB=AC, P是底边BC上一动点, PE∥AB, PF∥AC, 点E,F分别在AC, AB上.求证:PE+PF=AB.
A
B
C
E
F
P
环节三:应用知识 解决问题
请按下暂停键,3分钟后再继续学习
证明:∵ PE∥AB , PF∥AC,
∴ 四边形AFPE是平行四边形,
∴ AF=PE,AE=PF,
∵ AB=AC,∴ ∠B=∠C.
∵ PF∥AC,∴ ∠FPB=∠C,
∴ ∠B=∠FPB,∴ BF=PF.
∵ AB=AF+BF, ∴ PE+PF=AB.
(1)本节课我们学习了哪些知识?
(2)通过本节的学习和过去三角形的学习经历,你认
为对一个几何图形的研究通常是怎样进行的?
(3)对于平行四边形,你感兴趣的还有哪些方面?你
认为接下来可以研究什么问题?
课堂小结
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
