18.1.2三角形的中位线(第3课时)课件(共13张PPT)人教版八年级数学下学期1
文档属性
| 名称 | 18.1.2三角形的中位线(第3课时)课件(共13张PPT)人教版八年级数学下学期1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 14:44:05 | ||
图片预览





文档简介
(共13张PPT)
18.1.2三角形的中位线(第3课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
定义:如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE. 像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
问题2 看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
环节一:1.提出猜想
问题1 我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
DE∥BC,DE= BC
请按下暂停键,3分钟后再继续学习
2.分析思路
A
B
C
D
E
问题3 你能对照图形写出已知、求证吗?怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,说出辅助线的画法;如不可行,请说明原因.
请按下暂停键,4分钟后再继续学习
已知:△ABC中,D,E分别是边AB,AC 的中点,
求证:DE∥BC ,且DE= BC.
证明:延长DE至点F,使得EF=DE,连接DC,CF,AF,
∵ D,E分别是边AB,AC 的中点,∴ AD=BD,AE=EC,
∵ EF=DE,AE=EC,∴ 四边形ADCF是平行四边形.
∴ AD∥CF,AD=CF,
∵ BD=AD,∴ BD∥CF,BD=CF.
∴ 四边形BDFC是平行四边形.
∴ DF∥BC,DF=BC,
∵ EF=DE,∴ DE∥BC ,且DE= BC.
你还有其他证明方法吗?
问题4 比较证明方法的异同.请用自己的语言说出得到的结论.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
在△ABC中,
∵ D,E分别是边AB,AC的中点,
∴ DE∥BC,且DE= BC .
3.证明猜想
A
B
C
D
E
请按下暂停键,1分钟后再继续学习
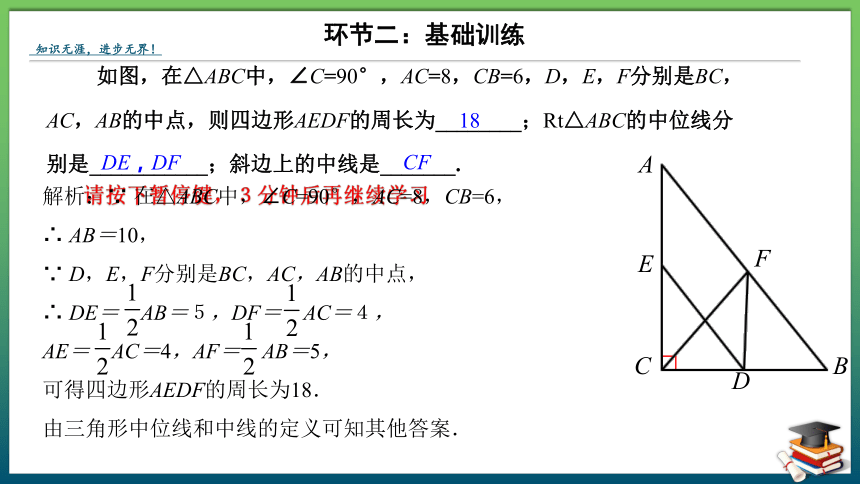
如图,在△ABC中,∠C=90°,AC=8,CB=6,D,E,F分别是BC,
AC,AB的中点,则四边形AEDF的周长为________;Rt△ABC的中位线分
别是___________;斜边上的中线是_______.
18
DE,DF
CF
环节二:基础训练
A
B
C
D
E
F
请按下暂停键,3分钟后再继续学习
解析:∵ 在△ABC中,∠C=90°,AC=8,CB=6,
∴ AB=10,
∵ D,E,F分别是BC,AC,AB的中点,
∴ DE= AB=5,DF= AC=4,
AE= AC=4,AF= AB=5,
可得四边形AEDF的周长为18.
由三角形中位线和中线的定义可知其他答案.
环节三:综合应用
例1 在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
请按下暂停键,5分钟后再继续学习
证明:连接BD,
∵ E,F,G,H分别是AB,BC,CD,DA的中点.
∴ EH∥BD,FG∥BD,EH= BD,FG= BD,
∵ EH=FG,EH∥FG,
∴ 四边形EFGH是平行四边形.
还有其他证明方法吗?
例2 已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
环节三:综合应用
请按下暂停键,3分钟后再继续学习
证明:取EB中点H,
∵ F是AE的中点,∴ FH∥AB,FH= AB,
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴ FH∥DC
∵ E是CD的中点,
∴ EC= DC,
∴ FH∥EC,FH=EC,
∴四边形EFHC是平行四边形,
∴ GF=GC.
例3 如图在△ABC中,D, E分别为AB, AC上的点,且BD=CE,M, N分别是BE, CD的中点.过MN的直线交AB于P,交AC于Q,线段AP, AQ相等吗 为什么
环节三:综合应用
请按下暂停键,3分钟后再继续学习
证明:取BC中点H,连接MH,NH,
∵ M、N分别是BE、CD的中点,
∴ MH∥EC, NH∥BD,MH= EC,NH= BD,
∵ BD=CE,∴ MH=NH,∴ ∠1=∠2,
∵ MH∥EC, NH∥BD,
∴ ∠1=∠4,∠2=∠3,
∴ ∠3=∠4,∴ AP=AQ.
例3 如图在△ABC中,D , E分别为AB、AC上的点,且BD=CE,M , N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP , AQ相等吗 为什么
环节三:综合应用
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会?
课堂小结
我们既可以用三角形知识研究平行四边形的问题,又可以用平行四边形知识研究三角形的问题.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
18.1.2三角形的中位线(第3课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
定义:如图,△ABC中,D,E分别是边AB,AC 的中点,连接DE. 像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
问题2 看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
环节一:1.提出猜想
问题1 我们在研究平行四边形时,经常采用把平行四边形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
DE∥BC,DE= BC
请按下暂停键,3分钟后再继续学习
2.分析思路
A
B
C
D
E
问题3 你能对照图形写出已知、求证吗?怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,说出辅助线的画法;如不可行,请说明原因.
请按下暂停键,4分钟后再继续学习
已知:△ABC中,D,E分别是边AB,AC 的中点,
求证:DE∥BC ,且DE= BC.
证明:延长DE至点F,使得EF=DE,连接DC,CF,AF,
∵ D,E分别是边AB,AC 的中点,∴ AD=BD,AE=EC,
∵ EF=DE,AE=EC,∴ 四边形ADCF是平行四边形.
∴ AD∥CF,AD=CF,
∵ BD=AD,∴ BD∥CF,BD=CF.
∴ 四边形BDFC是平行四边形.
∴ DF∥BC,DF=BC,
∵ EF=DE,∴ DE∥BC ,且DE= BC.
你还有其他证明方法吗?
问题4 比较证明方法的异同.请用自己的语言说出得到的结论.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
在△ABC中,
∵ D,E分别是边AB,AC的中点,
∴ DE∥BC,且DE= BC .
3.证明猜想
A
B
C
D
E
请按下暂停键,1分钟后再继续学习
如图,在△ABC中,∠C=90°,AC=8,CB=6,D,E,F分别是BC,
AC,AB的中点,则四边形AEDF的周长为________;Rt△ABC的中位线分
别是___________;斜边上的中线是_______.
18
DE,DF
CF
环节二:基础训练
A
B
C
D
E
F
请按下暂停键,3分钟后再继续学习
解析:∵ 在△ABC中,∠C=90°,AC=8,CB=6,
∴ AB=10,
∵ D,E,F分别是BC,AC,AB的中点,
∴ DE= AB=5,DF= AC=4,
AE= AC=4,AF= AB=5,
可得四边形AEDF的周长为18.
由三角形中位线和中线的定义可知其他答案.
环节三:综合应用
例1 在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
请按下暂停键,5分钟后再继续学习
证明:连接BD,
∵ E,F,G,H分别是AB,BC,CD,DA的中点.
∴ EH∥BD,FG∥BD,EH= BD,FG= BD,
∵ EH=FG,EH∥FG,
∴ 四边形EFGH是平行四边形.
还有其他证明方法吗?
例2 已知:如图,在□ABCD中,E是CD的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.
环节三:综合应用
请按下暂停键,3分钟后再继续学习
证明:取EB中点H,
∵ F是AE的中点,∴ FH∥AB,FH= AB,
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴ FH∥DC
∵ E是CD的中点,
∴ EC= DC,
∴ FH∥EC,FH=EC,
∴四边形EFHC是平行四边形,
∴ GF=GC.
例3 如图在△ABC中,D, E分别为AB, AC上的点,且BD=CE,M, N分别是BE, CD的中点.过MN的直线交AB于P,交AC于Q,线段AP, AQ相等吗 为什么
环节三:综合应用
请按下暂停键,3分钟后再继续学习
证明:取BC中点H,连接MH,NH,
∵ M、N分别是BE、CD的中点,
∴ MH∥EC, NH∥BD,MH= EC,NH= BD,
∵ BD=CE,∴ MH=NH,∴ ∠1=∠2,
∵ MH∥EC, NH∥BD,
∴ ∠1=∠4,∠2=∠3,
∴ ∠3=∠4,∴ AP=AQ.
例3 如图在△ABC中,D , E分别为AB、AC上的点,且BD=CE,M , N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP , AQ相等吗 为什么
环节三:综合应用
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)你有什么新的体会?
课堂小结
我们既可以用三角形知识研究平行四边形的问题,又可以用平行四边形知识研究三角形的问题.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
