18.2.1矩形的概念和性质(第1课时)课件(共24张PPT)2023-2024学年人教版八年级数学下学期
文档属性
| 名称 | 18.2.1矩形的概念和性质(第1课时)课件(共24张PPT)2023-2024学年人教版八年级数学下学期 |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
第 1 课时 | 矩形的概念和性质
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
请按下暂停键,2分钟后再继续学习
知识回顾
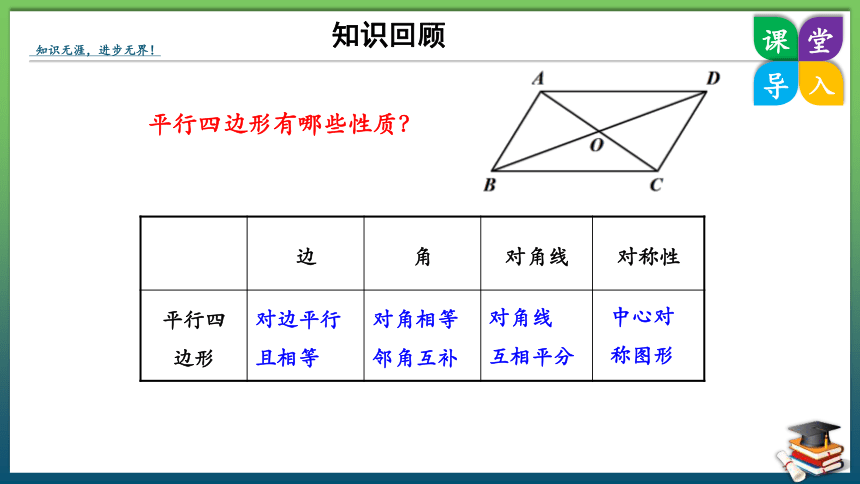
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
知识回顾
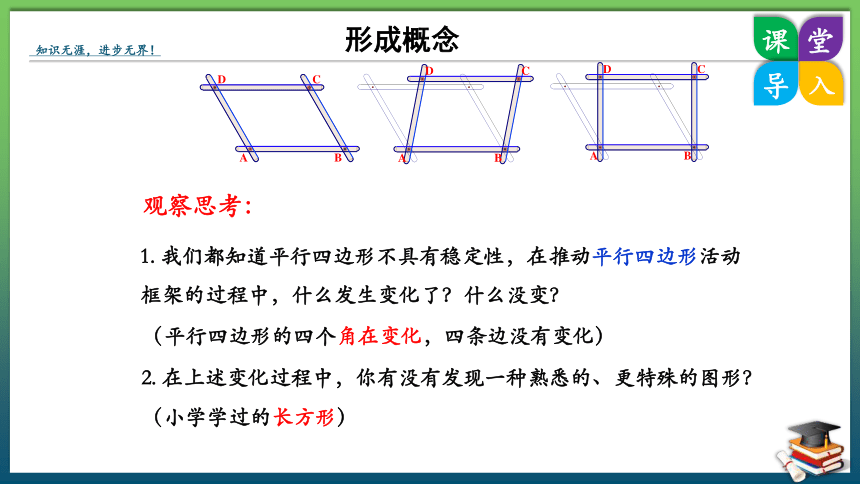
1. 我们都知道平行四边形不具有稳定性,在推动平行四边形活动框架的过程中,什么发生变化了?什么没变?
形成概念
观察思考:
2. 在上述变化过程中,你有没有发现一种熟悉的、更特殊的图形?
(小学学过的长方形)
(平行四边形的四个角在变化,四条边没有变化)
D
C
A
B
A
B
C
D
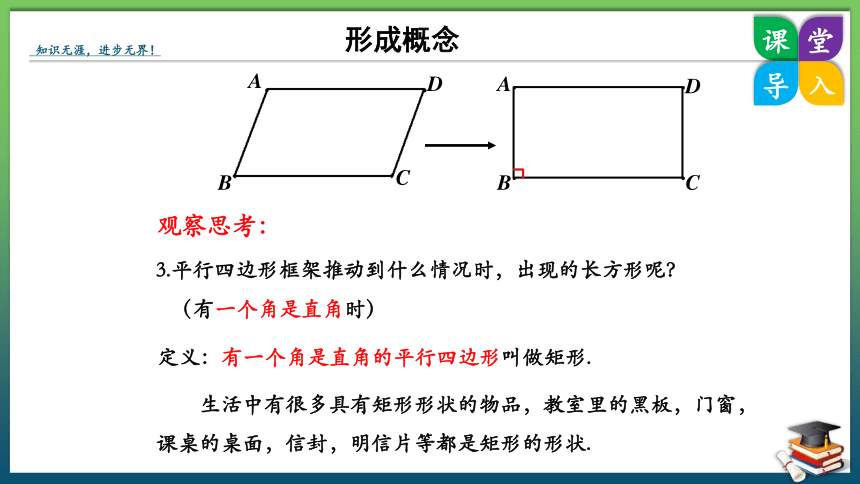
生活中有很多具有矩形形状的物品,教室里的黑板,门窗,课桌的桌面,信封,明信片等都是矩形的形状.
定义:有一个角是直角的平行四边形叫做矩形.
3.平行四边形框架推动到什么情况时,出现的长方形呢?
(有一个角是直角时)
观察思考:
形成概念
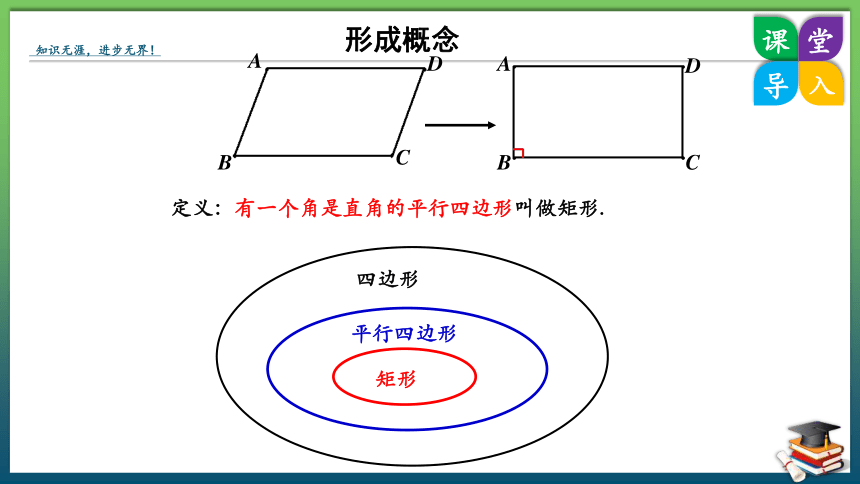
定义:有一个角是直角的平行四边形叫做矩形.
四边形
平行四边形
矩形
D
C
A
B
A
B
C
D
形成概念
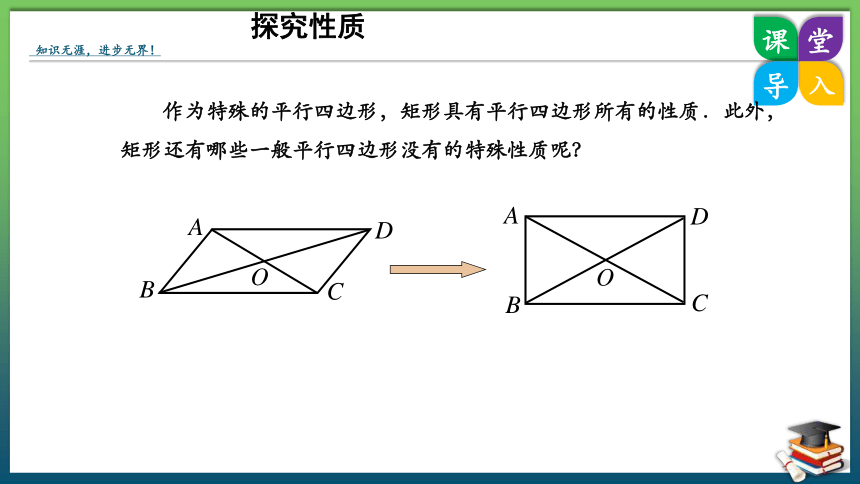
作为特殊的平行四边形,矩形具有平行四边形所有的性质.此外,矩形还有哪些一般平行四边形没有的特殊性质呢?
B
C
D
A
O
O
B
C
D
A
探究性质
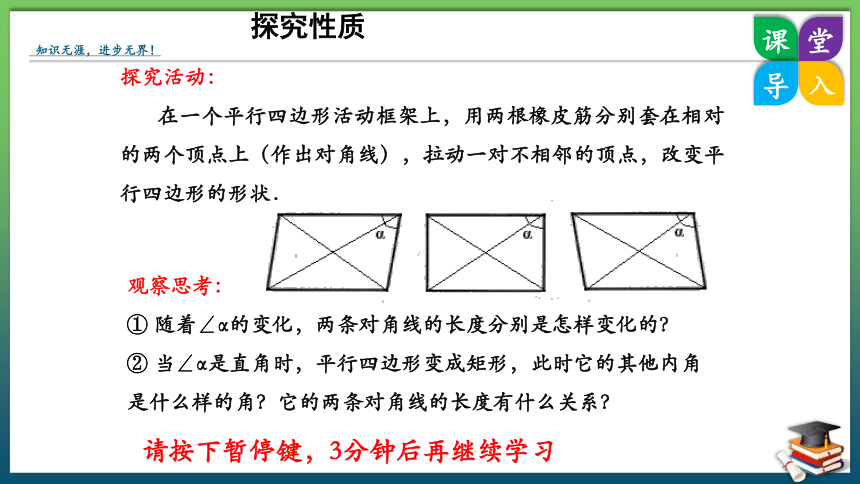
观察思考:
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
探究活动:
在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.
探究性质
请按下暂停键,3分钟后再继续学习
探究性质
观察结果:
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
随着∠α的变化,一条对角线在变长,一条在变短.
当∠α是直角时,其他内角也都是直角,两条对角线相等.
你能分别证明上述观察到的结果吗?
思考:
请按下暂停键,5分钟后再继续学习
命题: 矩形的四个角都是直角.
已知:如图,矩形ABCD中,∠A=90°.
证明:
∵ 四边形ABCD是矩形,
∴ 四边形ABCD是平行四边形.
∴ ∠C=∠A=90°, AB∥CD, AD∥BC,
∠B=180°-∠A=90°,
∠D=180°-∠A=90°.
求证:∠B=∠C=∠D=90°.
D
B
C
A
探究性质
定理: 矩形的四个角都是直角.
命题:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
分析:
根据矩形的性质可得AB=DC,∠ABC=∠DCB=90°.
又BC=CB,从而转化为证明△ABC与△DCB全等(SAS).
探究性质
B
C
D
A
请同学们课后自己完成证明过程.
定理:矩形的两条对角线相等.
矩形 数学语言
边 对边平行且相等 AB∥CD,AB=CD,AD∥BC,AD=BC
角 四个角都是直角 ∠A=∠B=∠C=∠D=90°
对角线 相等且互相平分 AC=BD,AO=OB=OC=OD
对称性 中心对称图形, 轴对称图形
O
B
C
D
A
探究性质
你在矩形中还发现了哪些基本图形?
A
B
C
D
O
探究性质
请按下暂停键,3分钟后再继续学习
A
B
C
D
O
两对全等的等腰三角形.
探究性质
A
B
C
D
O
四个全等的直角三角形.
探究性质
观察图中的Rt△ABC,在Rt△ABC中,OB是斜边AC上的中线,OB与AC有什么数量关系?
根据矩形的性质,可以得到: .
探究性质
B
C
O
A
∵ Rt△ABC中,O为斜边AC中点,
∴ OB= AC(或OA=OB=OC).
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
运用性质
例1 如图,矩形ABCD的两条对角线相交于点O,且∠AOB=60°,
AB=6 cm.求矩形对角线的长.
A
B
C
D
O
请按下暂停键,3分钟后再继续学习
运用性质
例1 如图,矩形ABCD的两条对角线相交于点O,且∠AOB=60°,
AB=6 cm.求矩形对角线的长.
A
B
C
D
O
解:∵ 矩形ABCD的两条对角线相交于点O,
∴ AO=OB=OC=OD.
∵ ∠AOB=60°,
∴ △AOB为等边三角形,
∴ AO=OB=AB=6 cm,
∴ AC=BD=12 cm.
例2 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.
A
B
C
O
∵ Rt△ABC中,O为斜边AC中点,
∴ OA=OB=OC.
解:三个人的位置对每个人是公平的,理由如下:
运用性质
例3 如图,矩形 ABCD中,AD长8 cm,对角线比AB边长4 cm.
求AB的长及点A到BD的距离AE的长.
运用性质
请按下暂停键,3分钟后再继续学习
例3 如图,矩形 ABCD中,AD长8 cm,对角线比AB边长4 cm.
求AB的长及点A到BD的距离AE的长.
略解:(1)设AB=x cm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理得: ,解得 x=6.则 AB=6 cm.
(2)“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×BD= AD×AB,解得 AE= 4.8 cm.
运用性质
3.直角三角形斜边上的中线等于斜边的一半.
4.矩形既是中心对称图形也是轴对称图形,连接对边中点的直线是
它的两条对称轴.
2.矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
1.矩形:有一个角是直角的平行四边形叫做矩形.
课堂小结
矩形的概念和性质
5.矩形的问题经常转化到等腰三角形或直角三角形中解决.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
第 1 课时 | 矩形的概念和性质
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
请按下暂停键,2分钟后再继续学习
知识回顾
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
知识回顾
1. 我们都知道平行四边形不具有稳定性,在推动平行四边形活动框架的过程中,什么发生变化了?什么没变?
形成概念
观察思考:
2. 在上述变化过程中,你有没有发现一种熟悉的、更特殊的图形?
(小学学过的长方形)
(平行四边形的四个角在变化,四条边没有变化)
D
C
A
B
A
B
C
D
生活中有很多具有矩形形状的物品,教室里的黑板,门窗,课桌的桌面,信封,明信片等都是矩形的形状.
定义:有一个角是直角的平行四边形叫做矩形.
3.平行四边形框架推动到什么情况时,出现的长方形呢?
(有一个角是直角时)
观察思考:
形成概念
定义:有一个角是直角的平行四边形叫做矩形.
四边形
平行四边形
矩形
D
C
A
B
A
B
C
D
形成概念
作为特殊的平行四边形,矩形具有平行四边形所有的性质.此外,矩形还有哪些一般平行四边形没有的特殊性质呢?
B
C
D
A
O
O
B
C
D
A
探究性质
观察思考:
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
探究活动:
在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.
探究性质
请按下暂停键,3分钟后再继续学习
探究性质
观察结果:
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
随着∠α的变化,一条对角线在变长,一条在变短.
当∠α是直角时,其他内角也都是直角,两条对角线相等.
你能分别证明上述观察到的结果吗?
思考:
请按下暂停键,5分钟后再继续学习
命题: 矩形的四个角都是直角.
已知:如图,矩形ABCD中,∠A=90°.
证明:
∵ 四边形ABCD是矩形,
∴ 四边形ABCD是平行四边形.
∴ ∠C=∠A=90°, AB∥CD, AD∥BC,
∠B=180°-∠A=90°,
∠D=180°-∠A=90°.
求证:∠B=∠C=∠D=90°.
D
B
C
A
探究性质
定理: 矩形的四个角都是直角.
命题:矩形的两条对角线相等.
已知:AC,BD是矩形ABCD的两条对角线.
求证: AC=BD.
分析:
根据矩形的性质可得AB=DC,∠ABC=∠DCB=90°.
又BC=CB,从而转化为证明△ABC与△DCB全等(SAS).
探究性质
B
C
D
A
请同学们课后自己完成证明过程.
定理:矩形的两条对角线相等.
矩形 数学语言
边 对边平行且相等 AB∥CD,AB=CD,AD∥BC,AD=BC
角 四个角都是直角 ∠A=∠B=∠C=∠D=90°
对角线 相等且互相平分 AC=BD,AO=OB=OC=OD
对称性 中心对称图形, 轴对称图形
O
B
C
D
A
探究性质
你在矩形中还发现了哪些基本图形?
A
B
C
D
O
探究性质
请按下暂停键,3分钟后再继续学习
A
B
C
D
O
两对全等的等腰三角形.
探究性质
A
B
C
D
O
四个全等的直角三角形.
探究性质
观察图中的Rt△ABC,在Rt△ABC中,OB是斜边AC上的中线,OB与AC有什么数量关系?
根据矩形的性质,可以得到: .
探究性质
B
C
O
A
∵ Rt△ABC中,O为斜边AC中点,
∴ OB= AC(或OA=OB=OC).
直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
运用性质
例1 如图,矩形ABCD的两条对角线相交于点O,且∠AOB=60°,
AB=6 cm.求矩形对角线的长.
A
B
C
D
O
请按下暂停键,3分钟后再继续学习
运用性质
例1 如图,矩形ABCD的两条对角线相交于点O,且∠AOB=60°,
AB=6 cm.求矩形对角线的长.
A
B
C
D
O
解:∵ 矩形ABCD的两条对角线相交于点O,
∴ AO=OB=OC=OD.
∵ ∠AOB=60°,
∴ △AOB为等边三角形,
∴ AO=OB=AB=6 cm,
∴ AC=BD=12 cm.
例2 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处.三个人的位置对每个人公平吗?请说明理由.
A
B
C
O
∵ Rt△ABC中,O为斜边AC中点,
∴ OA=OB=OC.
解:三个人的位置对每个人是公平的,理由如下:
运用性质
例3 如图,矩形 ABCD中,AD长8 cm,对角线比AB边长4 cm.
求AB的长及点A到BD的距离AE的长.
运用性质
请按下暂停键,3分钟后再继续学习
例3 如图,矩形 ABCD中,AD长8 cm,对角线比AB边长4 cm.
求AB的长及点A到BD的距离AE的长.
略解:(1)设AB=x cm,则对角线长(x+4)cm,在Rt△ABD中,由勾股定理得: ,解得 x=6.则 AB=6 cm.
(2)“直角三角形斜边上的高”是一个基本图形,利用面积公式,可得到两直角边、斜边及斜边上的高的一个基本关系式: AE×BD= AD×AB,解得 AE= 4.8 cm.
运用性质
3.直角三角形斜边上的中线等于斜边的一半.
4.矩形既是中心对称图形也是轴对称图形,连接对边中点的直线是
它的两条对称轴.
2.矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
1.矩形:有一个角是直角的平行四边形叫做矩形.
课堂小结
矩形的概念和性质
5.矩形的问题经常转化到等腰三角形或直角三角形中解决.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
