18.2.2矩形的判定(第2课时)课件(共23张PPT)2023-2024学年人教版八年级数学下学期
文档属性
| 名称 | 18.2.2矩形的判定(第2课时)课件(共23张PPT)2023-2024学年人教版八年级数学下学期 |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
18.2.2矩形的判定(第2课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
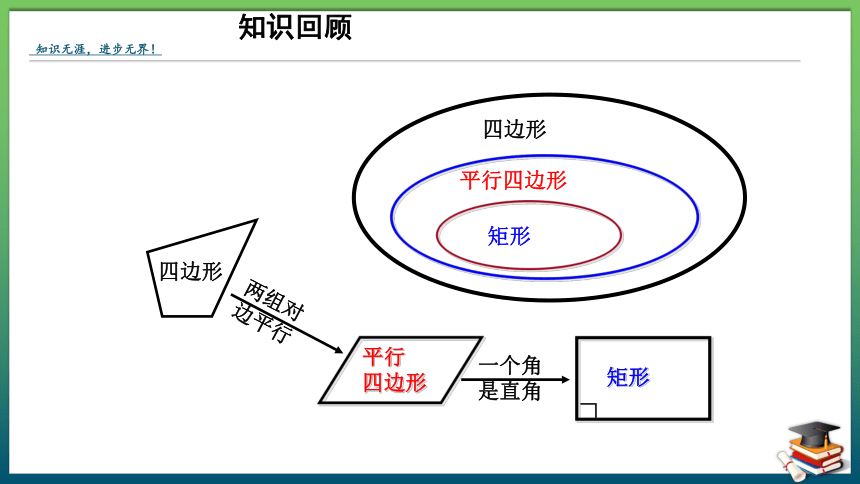
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形
矩形
四边形
知识回顾
1、矩形的四个内角都是______.
2、矩形的对角线______且 __________.
3、矩形是______________对称图形.
4、在直角三角形中,______角所对的直角边等于斜边的_______.
5、在直角三角形中,斜边上的______等于斜边的______.
请按下暂停键,3分钟后再继续学习
知识回顾
1、矩形的四个内角都是______.
2、矩形的对角线______且 __________.
直角
相等
互相平分
3、矩形是______________对称图形.
轴对称和中心
4、在直角三角形中,______角所对的直角边等于斜边的_______.
5、在直角三角形中,斜边上的______等于斜边的______.
30°
一半
中线
一半
知识回顾
测量…?
木工师傅在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
情景引入
你有办法帮他吗?
请按下暂停键,3分钟后再继续学习
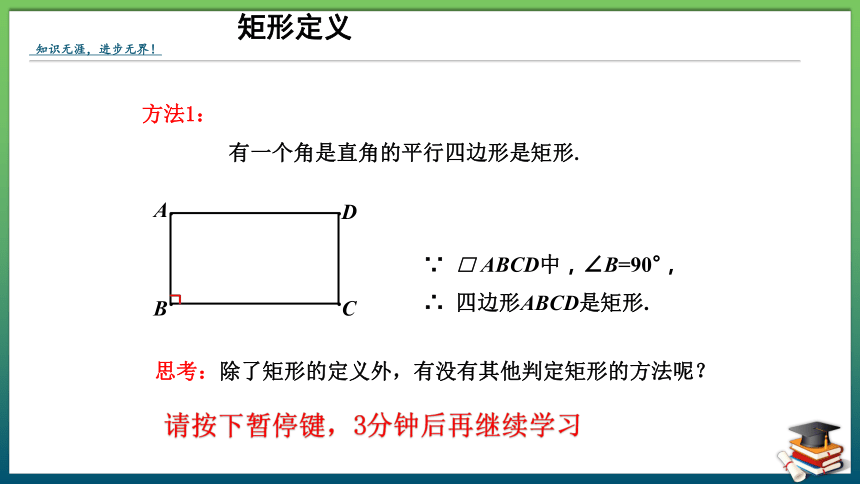
方法1:
有一个角是直角的平行四边形是矩形.
∵ □ ABCD中,∠B=90°,
∴ 四边形ABCD是矩形.
矩形定义
A
B
C
D
思考:除了矩形的定义外,有没有其他判定矩形的方法呢?
请按下暂停键,3分钟后再继续学习
证明
逆命题
(修正)
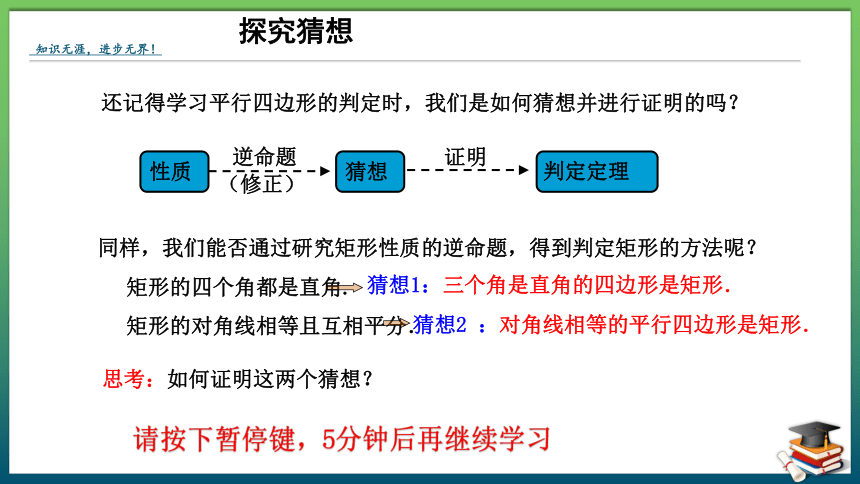
还记得学习平行四边形的判定时,我们是如何猜想并进行证明的吗?
性质
猜想
判定定理
探究猜想
同样,我们能否通过研究矩形性质的逆命题,得到判定矩形的方法呢?
矩形的四个角都是直角.
矩形的对角线相等且互相平分.
思考:如何证明这两个猜想?
请按下暂停键,5分钟后再继续学习
猜想1:三个角是直角的四边形是矩形.
猜想2 :对角线相等的平行四边形是矩形.
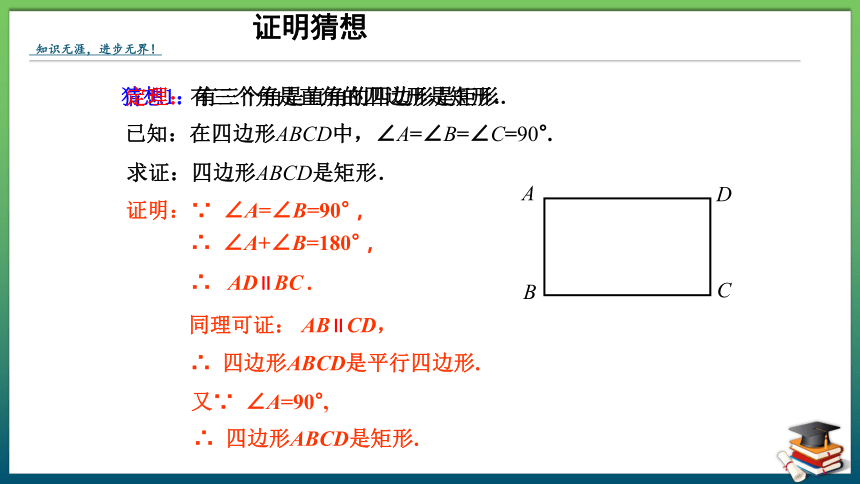
证明猜想
猜想1:有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
B
C
D
A
证明:∵ ∠A=∠B=90°,
∴ ∠A+∠B=180°,
∴ AD∥BC .
同理可证: AB∥CD,
∴ 四边形ABCD是平行四边形.
又∵ ∠A=90°,
∴ 四边形ABCD是矩形.
定理:有三个角是直角的四边形是矩形.
猜想2:对角线相等的平行四边形是矩形.
已知:在 ABCD中,AC=BD.求证:四边形ABCD是矩形.
B
C
D
A
∴ △ABC≌△DCB(SSS),
∵ AB∥DC,
又∵ 四边形ABCD是平行四边形,
∴ 四边形ABCD是矩形.
∴ ∠ABC=∠DCB .
又∵ BC=CB,且AC=DB,
∴ ∠ABC+∠DCB=180°,
∴ ∠ABC=∠DCB=90°.
证明:∵ 四边形 ABCD是平行四边形,
∴ AB=DC 且 AB∥DC .
证明猜想
定理:对角线相等的平行四边形是矩形.
方法1:有一个角是直角的平行四边形叫做矩形;
方法2:有三个角是直角的四边形是矩形;
方法3:对角线相等的平行四边形是矩形.
你能归纳矩形的判定方法吗?
运用判定
现在你可以帮助木工师傅检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
测量…?
请按下暂停键,5分钟后再继续学习
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格.
方案1:
依据:先用两组对边分别相等判定是平行四边形,再用定义判定是矩形.
运用判定
测量出三个内角的度数,如果三个内角都是
直角,则窗框符合规格.
依据:有三个角是直角的四边形是矩形.
运用判定
方案2:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格.
依据:先用两组对边分别相等判定是平行四边形,再用对角线相等判定是矩形.
运用判定
方案3:
分别测量出一组对边的长度和这组同旁内角的度数,如果这组对边的长度相等,且这两个内角都是直角,则窗框符合规格.
依据:先用一组对边平行且相等判定是平行四边形,再用定义判定是矩形.
运用判定
方案4:
例1 下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形. ( )
(4)对角线相等的四边形是矩形. ( )
(5)对角线互相平分且相等的四边形是矩形.( )
(3)四个角都是直角的四边形是矩形.( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
运用判定
请按下暂停键,3分钟后再继续学习
例1 下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形.( )
×
(2)四个角都相等的四边形是矩形. ( )
√
(4)对角线相等的四边形是矩形. ( )
(5)对角线互相平分且相等的四边形是矩形.( )
(3)四个角都是直角的四边形是矩形.( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
运用判定
√
√
√
×
A
O
B
D
C
例2 已知:如图,四边形ABCD中,AO=BO=CO=DO,
试证明四边形ABCD是矩形.
运用判定
请按下暂停键,3分钟后再继续学习
A
O
B
D
C
例2 已知:如图,四边形ABCD中,AO=BO=CO=DO,
试证明四边形ABCD是矩形.
证明:
∵ AO=BO=CO=DO,
∴ AO=CO,BO=DO,
∴ 四边形ABCD是平行四边形.
即 AC=BD,
∴ 四边形ABCD是矩形.
又∵ AO+CO=BO+DO,
运用判定
A
B
D
C
H
E
F
G
例3 如图, ABCD四个内角的平分线围成四边形EFGH,猜想
四边形EFGH的形状,并说明理由.
运用判定
请按下暂停键,3分钟后再继续学习
A
B
D
C
H
E
F
G
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,
∴ ∠DAB+∠ABC=180 °.
例3 如图, ABCD四个内角的平分线围成四边形EFGH,猜想
四边形EFGH的形状,并说明理由.
证明: 四边形EFGH是矩形,理由如下:
同理:∠EFG=90°,∠FGH=90°,
∴ 四边形EFGH是矩形.
∵ AE、BE分别平分∠DAB、∠ABC , ∴ ∠EAB+∠EBA=90°,
∴ ∠AEB=90°,∴ ∠HEF=90°.
运用判定
判定一个四边形是矩形的方法有:
课堂小结
矩形的判定
要根据条件灵活选择使用判定方法.
方法1:有一个角是直角的平行四边形叫做矩形;
方法2:有三个角是直角的四边形是矩形;
方法3:对角线相等的平行四边形是矩形.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
18.2.2矩形的判定(第2课时)
第十八章 平形四边形
任 课 教 师 | X X X
人教版八年级数学下册
知识无涯,进步无界!
新理念
新课标
新征程
四边形
平行
四边形
两组对
边平行
一个角
是直角
∟
矩形
平行四边形
矩形
四边形
知识回顾
1、矩形的四个内角都是______.
2、矩形的对角线______且 __________.
3、矩形是______________对称图形.
4、在直角三角形中,______角所对的直角边等于斜边的_______.
5、在直角三角形中,斜边上的______等于斜边的______.
请按下暂停键,3分钟后再继续学习
知识回顾
1、矩形的四个内角都是______.
2、矩形的对角线______且 __________.
直角
相等
互相平分
3、矩形是______________对称图形.
轴对称和中心
4、在直角三角形中,______角所对的直角边等于斜边的_______.
5、在直角三角形中,斜边上的______等于斜边的______.
30°
一半
中线
一半
知识回顾
测量…?
木工师傅在制作窗框后,需要检测所制作的窗框是否是矩形,那么他需要测量哪些数据,其根据又是什么呢?
情景引入
你有办法帮他吗?
请按下暂停键,3分钟后再继续学习
方法1:
有一个角是直角的平行四边形是矩形.
∵ □ ABCD中,∠B=90°,
∴ 四边形ABCD是矩形.
矩形定义
A
B
C
D
思考:除了矩形的定义外,有没有其他判定矩形的方法呢?
请按下暂停键,3分钟后再继续学习
证明
逆命题
(修正)
还记得学习平行四边形的判定时,我们是如何猜想并进行证明的吗?
性质
猜想
判定定理
探究猜想
同样,我们能否通过研究矩形性质的逆命题,得到判定矩形的方法呢?
矩形的四个角都是直角.
矩形的对角线相等且互相平分.
思考:如何证明这两个猜想?
请按下暂停键,5分钟后再继续学习
猜想1:三个角是直角的四边形是矩形.
猜想2 :对角线相等的平行四边形是矩形.
证明猜想
猜想1:有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
B
C
D
A
证明:∵ ∠A=∠B=90°,
∴ ∠A+∠B=180°,
∴ AD∥BC .
同理可证: AB∥CD,
∴ 四边形ABCD是平行四边形.
又∵ ∠A=90°,
∴ 四边形ABCD是矩形.
定理:有三个角是直角的四边形是矩形.
猜想2:对角线相等的平行四边形是矩形.
已知:在 ABCD中,AC=BD.求证:四边形ABCD是矩形.
B
C
D
A
∴ △ABC≌△DCB(SSS),
∵ AB∥DC,
又∵ 四边形ABCD是平行四边形,
∴ 四边形ABCD是矩形.
∴ ∠ABC=∠DCB .
又∵ BC=CB,且AC=DB,
∴ ∠ABC+∠DCB=180°,
∴ ∠ABC=∠DCB=90°.
证明:∵ 四边形 ABCD是平行四边形,
∴ AB=DC 且 AB∥DC .
证明猜想
定理:对角线相等的平行四边形是矩形.
方法1:有一个角是直角的平行四边形叫做矩形;
方法2:有三个角是直角的四边形是矩形;
方法3:对角线相等的平行四边形是矩形.
你能归纳矩形的判定方法吗?
运用判定
现在你可以帮助木工师傅检测所制作的窗框是否是矩形了吧,你可以测量哪些数据,有几种方案,根据又是什么呢?
测量…?
请按下暂停键,5分钟后再继续学习
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则窗框符合规格.
方案1:
依据:先用两组对边分别相等判定是平行四边形,再用定义判定是矩形.
运用判定
测量出三个内角的度数,如果三个内角都是
直角,则窗框符合规格.
依据:有三个角是直角的四边形是矩形.
运用判定
方案2:
分别测量出窗框四边和两条对角线的长度,如果窗框两组对边长度、两条对角线的长度分别相等,那么窗框符合规格.
依据:先用两组对边分别相等判定是平行四边形,再用对角线相等判定是矩形.
运用判定
方案3:
分别测量出一组对边的长度和这组同旁内角的度数,如果这组对边的长度相等,且这两个内角都是直角,则窗框符合规格.
依据:先用一组对边平行且相等判定是平行四边形,再用定义判定是矩形.
运用判定
方案4:
例1 下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形. ( )
(4)对角线相等的四边形是矩形. ( )
(5)对角线互相平分且相等的四边形是矩形.( )
(3)四个角都是直角的四边形是矩形.( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
运用判定
请按下暂停键,3分钟后再继续学习
例1 下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形.( )
×
(2)四个角都相等的四边形是矩形. ( )
√
(4)对角线相等的四边形是矩形. ( )
(5)对角线互相平分且相等的四边形是矩形.( )
(3)四个角都是直角的四边形是矩形.( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
运用判定
√
√
√
×
A
O
B
D
C
例2 已知:如图,四边形ABCD中,AO=BO=CO=DO,
试证明四边形ABCD是矩形.
运用判定
请按下暂停键,3分钟后再继续学习
A
O
B
D
C
例2 已知:如图,四边形ABCD中,AO=BO=CO=DO,
试证明四边形ABCD是矩形.
证明:
∵ AO=BO=CO=DO,
∴ AO=CO,BO=DO,
∴ 四边形ABCD是平行四边形.
即 AC=BD,
∴ 四边形ABCD是矩形.
又∵ AO+CO=BO+DO,
运用判定
A
B
D
C
H
E
F
G
例3 如图, ABCD四个内角的平分线围成四边形EFGH,猜想
四边形EFGH的形状,并说明理由.
运用判定
请按下暂停键,3分钟后再继续学习
A
B
D
C
H
E
F
G
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,
∴ ∠DAB+∠ABC=180 °.
例3 如图, ABCD四个内角的平分线围成四边形EFGH,猜想
四边形EFGH的形状,并说明理由.
证明: 四边形EFGH是矩形,理由如下:
同理:∠EFG=90°,∠FGH=90°,
∴ 四边形EFGH是矩形.
∵ AE、BE分别平分∠DAB、∠ABC , ∴ ∠EAB+∠EBA=90°,
∴ ∠AEB=90°,∴ ∠HEF=90°.
运用判定
判定一个四边形是矩形的方法有:
课堂小结
矩形的判定
要根据条件灵活选择使用判定方法.
方法1:有一个角是直角的平行四边形叫做矩形;
方法2:有三个角是直角的四边形是矩形;
方法3:对角线相等的平行四边形是矩形.
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
