六年级下册数学人教版圆柱的体积课件(共31张PPT)
文档属性
| 名称 | 六年级下册数学人教版圆柱的体积课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
第三单元 圆柱与圆锥 第1课 圆柱
圆柱的体积(3)
人教版六年级下册数学课件
复习导入
第一部分
PART 01
西红柿
土豆
梨
石块
像这些形状不规则的物体,怎么求它们的体积呢?
放入后
上升部分的水的体积
( 升水法 )不规则物体的体积= 上升部分水的体积
( 降水法 ) 不规则物体的体积=
( 溢水法1)不规则物体的体积=
V物 = V上升部分水+V溢出部分水
物体必须完全浸没
V物 = V上升部分水
V物 = V下降部分水
V物 = V溢出部分水
( 溢水法2)不规则物体的体积= +
下降部分水的体积
溢出部分水的体积
上升部分水的体积
溢出部分水的体积
西红柿
土豆
梨
石块
把不规则物体( )成了规则物体
转化
如何求瓶子的体积或者容积呢?
1.通过观察比较,掌握不规则物体的体积的计算方法(重点)
2.培养利用所学知识灵活解决实际问题的能力,并逐步参透“转化”的数学思想。(难点)
学习目标
一个底面内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少
探索新知
模块一:圆柱形容器容积的计算
自学指导:
1、从题中你得到了哪些信息?条件是?问题是?
2、瓶子的容积包含了几部分?
一个底面内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少
探索新知
模块一:圆柱形容器容积的计算
自学指导:自学课本第26页,回答以下问题。
3、倒置前和倒置后,水有什么变化?( )变了,
( )不变。
4、倒置前和倒置后,空白部分的体积有什么关系?
5、瓶子的容积=( )的体积+( )的体积
活动:独立思考后小组讨论。
形状
体积
倒置前水
倒置后空白部分
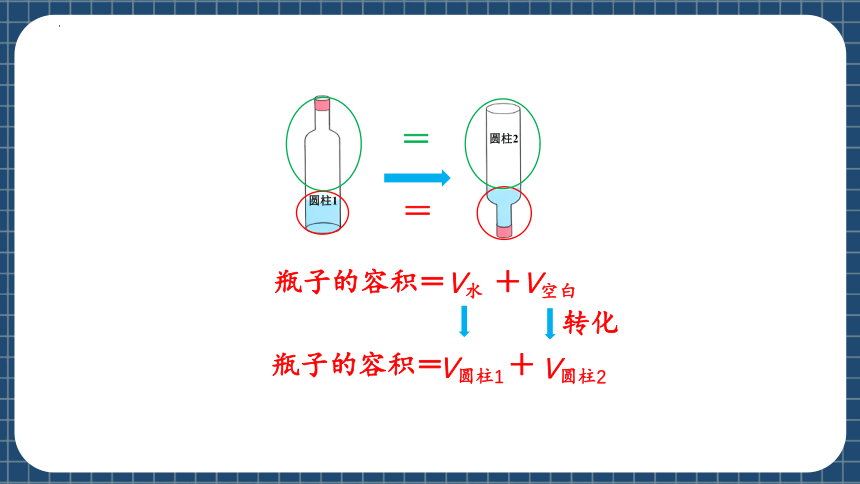
瓶子的容积=V水 +V空白
=
=
转化
瓶子的容积= +
圆柱1
圆柱2
V圆柱1
V圆柱2
瓶子的容积转化成两个圆柱的体积。
要计算这两个圆柱的体积需要知道哪些信息?请你独立完成计算。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256 (mL)
答:这个瓶子的容积是1256mL。
思
考
你还能想到别的方法吗?
7cm
18cm
1
2
7cm
18cm
答:这个瓶子的容积是1256mL。
瓶子的容积:
3.14×(8÷2)2×( 7+18 )
=3.14×16×25
=1256 (cm )
=1256 (mL)
7cm
18cm
回顾与反思
在五年级计算梨的体积时,也是用了转化的方法。
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算体积。
1.如图,一个醋瓶里面深 30 cm,底面内直径 10 cm,瓶子里醋的高度是 15 cm。把瓶口塞紧后,使其瓶口向下倒立,这时醋深 25 cm。醋瓶的容积是多少毫升?
3.14×(10÷2)2×(30-25+15)
= 1570(cm3)
= 1570(mL)
随堂练习
答:醋瓶的容积是1570mL。
2.往一个底面直径是 8 cm,高 10 cm 的圆柱形玻璃杯内倒入水,水面高 8 cm。把一个小球浸没在杯内,水满后还溢出 12.52 mL。求小球的体积。
12.52 mL=12.52 cm3
3.14×(8÷2)2×(10-8)+12.52=113(cm3)
拓展延伸
答:小球的体积是113cm3。
还有其他方法求瓶子的体积或者容积吗?
同学们,今天的数学课你们有哪些收获呢?
课堂小结
课堂小结
第三部分
PART 03
2.如图,一个油瓶,瓶身是圆柱形,容积是 500 mL。瓶里装有一些油,正放时,油深 18 cm,盖紧瓶盖倒放时,空余部分高 2 cm。求瓶中油的体积。
500 mL = 500 cm3 500÷(18+2)×18 = 450(cm3) 450 cm 3= 450 mL
答:瓶中油的体积是450mL。
2.一个装水的圆柱形容器的底面内直径是10cm,一个铁块完全浸没在这个容器的水中,将铁块取出后,水面下降2cm。这个铁块的体积是多少?
3.14×(10÷2)2×2=157(cm3)
答:这块铁块的体积是157cm3。
铁块的体积=下降部分水的体积
3.*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
第一个图
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个图
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
第三个图
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个图
3.14×(6÷3.14÷2)2×6≈17.20(dm3)
答:以18dm为圆柱的底面周长、2dm为高的圆柱体体积最大;以2dm为圆柱的底面周长、18dm为高的圆柱体体积最小。
你有什么发现?
当圆柱的侧面积相同时,底面半径(或周长)大的体积就大。
3. 一瓶装满果汁的饮料瓶的内直径是 8 cm,状状全家喝了一些,把瓶盖拧紧后倒置放平,空的部分高 15 cm。状状全家喝了多少果汁?
3.14×(8÷2)2×15
= 753.6(cm3)
= 753.6(mL)
1.两个底面积相等的圆柱,一个高为4.5dm,体积为81dm3。另一个高为3dm,它的体积是多少?
81÷4.5×3=54(dm3)
答:它的体积是54dm3。
随堂练习
第三单元 圆柱与圆锥 第1课 圆柱
圆柱的体积(3)
人教版六年级下册数学课件
复习导入
第一部分
PART 01
西红柿
土豆
梨
石块
像这些形状不规则的物体,怎么求它们的体积呢?
放入后
上升部分的水的体积
( 升水法 )不规则物体的体积= 上升部分水的体积
( 降水法 ) 不规则物体的体积=
( 溢水法1)不规则物体的体积=
V物 = V上升部分水+V溢出部分水
物体必须完全浸没
V物 = V上升部分水
V物 = V下降部分水
V物 = V溢出部分水
( 溢水法2)不规则物体的体积= +
下降部分水的体积
溢出部分水的体积
上升部分水的体积
溢出部分水的体积
西红柿
土豆
梨
石块
把不规则物体( )成了规则物体
转化
如何求瓶子的体积或者容积呢?
1.通过观察比较,掌握不规则物体的体积的计算方法(重点)
2.培养利用所学知识灵活解决实际问题的能力,并逐步参透“转化”的数学思想。(难点)
学习目标
一个底面内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少
探索新知
模块一:圆柱形容器容积的计算
自学指导:
1、从题中你得到了哪些信息?条件是?问题是?
2、瓶子的容积包含了几部分?
一个底面内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧,把瓶子倒置、放平,无水部分是圆柱形,高度是18cm。这个瓶子的容积是多少
探索新知
模块一:圆柱形容器容积的计算
自学指导:自学课本第26页,回答以下问题。
3、倒置前和倒置后,水有什么变化?( )变了,
( )不变。
4、倒置前和倒置后,空白部分的体积有什么关系?
5、瓶子的容积=( )的体积+( )的体积
活动:独立思考后小组讨论。
形状
体积
倒置前水
倒置后空白部分
瓶子的容积=V水 +V空白
=
=
转化
瓶子的容积= +
圆柱1
圆柱2
V圆柱1
V圆柱2
瓶子的容积转化成两个圆柱的体积。
要计算这两个圆柱的体积需要知道哪些信息?请你独立完成计算。
瓶子的容积:
3.14×(8÷2)2×7+3.14×(8÷2)2×18
=3.14×16×(7+18)
=3.14×16×25
=1256 (cm )
=1256 (mL)
答:这个瓶子的容积是1256mL。
思
考
你还能想到别的方法吗?
7cm
18cm
1
2
7cm
18cm
答:这个瓶子的容积是1256mL。
瓶子的容积:
3.14×(8÷2)2×( 7+18 )
=3.14×16×25
=1256 (cm )
=1256 (mL)
7cm
18cm
回顾与反思
在五年级计算梨的体积时,也是用了转化的方法。
我们利用了体积不变的特性,把不规则图形转化成规则图形来计算体积。
1.如图,一个醋瓶里面深 30 cm,底面内直径 10 cm,瓶子里醋的高度是 15 cm。把瓶口塞紧后,使其瓶口向下倒立,这时醋深 25 cm。醋瓶的容积是多少毫升?
3.14×(10÷2)2×(30-25+15)
= 1570(cm3)
= 1570(mL)
随堂练习
答:醋瓶的容积是1570mL。
2.往一个底面直径是 8 cm,高 10 cm 的圆柱形玻璃杯内倒入水,水面高 8 cm。把一个小球浸没在杯内,水满后还溢出 12.52 mL。求小球的体积。
12.52 mL=12.52 cm3
3.14×(8÷2)2×(10-8)+12.52=113(cm3)
拓展延伸
答:小球的体积是113cm3。
还有其他方法求瓶子的体积或者容积吗?
同学们,今天的数学课你们有哪些收获呢?
课堂小结
课堂小结
第三部分
PART 03
2.如图,一个油瓶,瓶身是圆柱形,容积是 500 mL。瓶里装有一些油,正放时,油深 18 cm,盖紧瓶盖倒放时,空余部分高 2 cm。求瓶中油的体积。
500 mL = 500 cm3 500÷(18+2)×18 = 450(cm3) 450 cm 3= 450 mL
答:瓶中油的体积是450mL。
2.一个装水的圆柱形容器的底面内直径是10cm,一个铁块完全浸没在这个容器的水中,将铁块取出后,水面下降2cm。这个铁块的体积是多少?
3.14×(10÷2)2×2=157(cm3)
答:这块铁块的体积是157cm3。
铁块的体积=下降部分水的体积
3.*下面4个图形的面积都是36dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?(单位:dm)
第一个图
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个图
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
第三个图
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个图
3.14×(6÷3.14÷2)2×6≈17.20(dm3)
答:以18dm为圆柱的底面周长、2dm为高的圆柱体体积最大;以2dm为圆柱的底面周长、18dm为高的圆柱体体积最小。
你有什么发现?
当圆柱的侧面积相同时,底面半径(或周长)大的体积就大。
3. 一瓶装满果汁的饮料瓶的内直径是 8 cm,状状全家喝了一些,把瓶盖拧紧后倒置放平,空的部分高 15 cm。状状全家喝了多少果汁?
3.14×(8÷2)2×15
= 753.6(cm3)
= 753.6(mL)
1.两个底面积相等的圆柱,一个高为4.5dm,体积为81dm3。另一个高为3dm,它的体积是多少?
81÷4.5×3=54(dm3)
答:它的体积是54dm3。
随堂练习
