人教版八年级数学上册试题12.2三角形全等的判定(SSS和SAS)同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册试题12.2三角形全等的判定(SSS和SAS)同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-16 00:00:00 | ||
图片预览

文档简介
12.2三角形全等的判定(SSS和SAS)
一、单选题
1.以下生活现象不是利用三角形稳定性的是( )
A. B. C. D.
2.如图是尺规作图法作的平分线时的痕迹图,能判定的理由是( )
A. B. C. D.
3.如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
4.如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B.
C. D.
5.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是( )
A. B.EN=a C.∠E=60° D.∠N=66°
6.如图,在中,,,点是边上的中点,则的长满足的条件是( )
A. B. C. D.
7.如图,一块三角形的玻璃碎成3块(图中所标1、2、3),小华带第3块碎片去玻璃店,购买形状相同、大小相等的新玻璃,这是利用三角形全等中的( )
A. B. C. D.
8.如图,和都是等腰直角三角形,,则的度数是( )
A. B. C. D.
9.已知,如图所示的网格是由9个相同的小正方形拼成的,图中的各个顶点均为格点,则的度数为( )
A. B. C. D.
10.如图,在四边形ABDE中,,,点C是边BD上一点,,,.下列结论:①;②;③四边形的面积是;④;其中正确的结论个数是( )
A.4 B.3 C.2 D.1
二、填空题
11.数学课上,老师出示如下题目:“已知:.求作:.”如图是小宇用直尺和圆规的作法,其中的道理是作出△,根据全等三角形的性质,得到.△的依据是 .
12.如图,已知,,若,则 度.
13.如图,在△ABC中,D是BC上的一点,CA=CD,CE平分∠ACB,交AB于点E,连接DE,若∠A=100°,∠B=45°,则∠BED= °.
14.如图,是外一点,是上一点,,,,,则的度数为 .
15.如图,△ABC中,∠BAC=2∠C,BD为∠ABC的平分线,BC=7.6,AB=4.4,则AD= .
16.如图,在中,,是高,E是外一点,,连接,,若,,,则的面积为 .
17.如图,在中,,、分别是、边上的高,在上取点,使,在射线上取点,使,连接、,若,,则 .
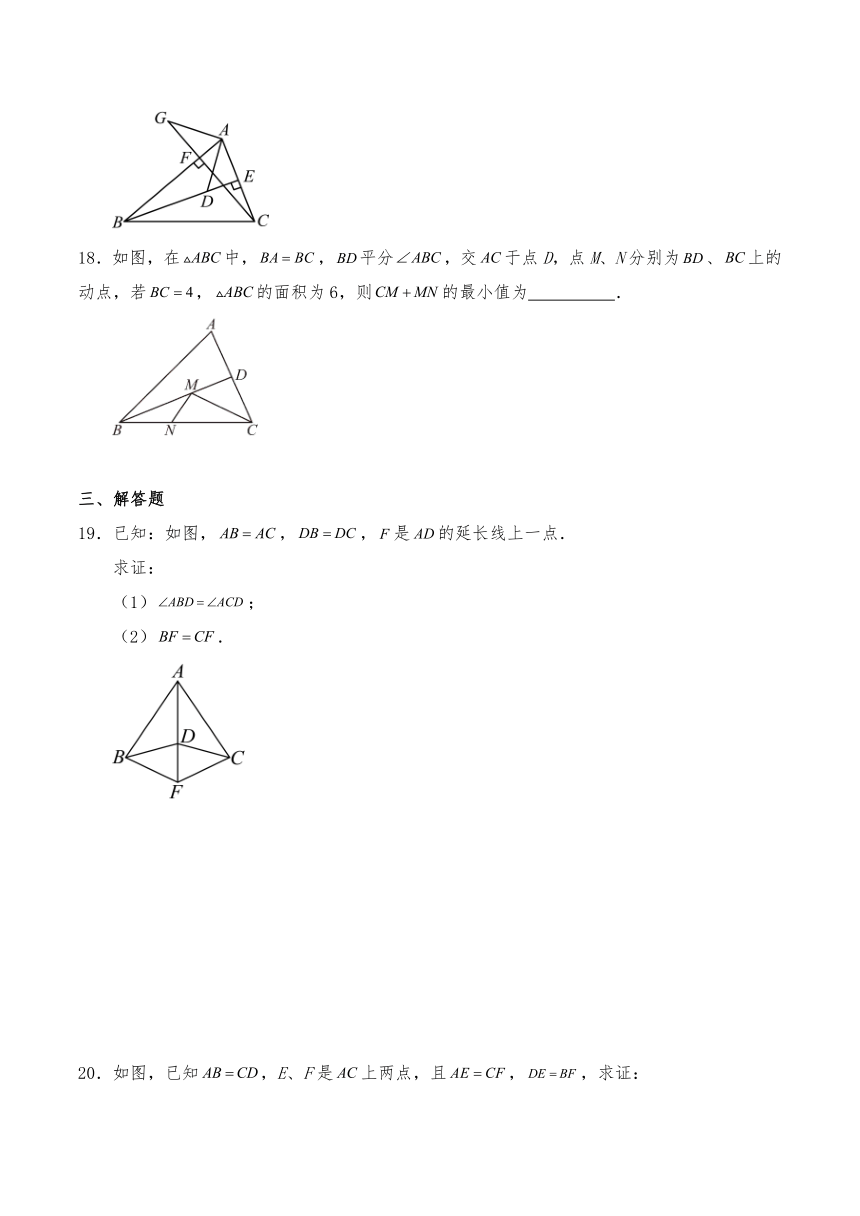
18.如图,在中,,平分,交于点D,点M、N分别为、上的动点,若,的面积为6,则的最小值为 .
三、解答题
19.已知:如图,,,是的延长线上一点.
求证:
(1);
(2).
20.如图,已知,E、F是上两点,且,,求证:
(1).
(2).
21.如图,的边与的边在一条直线上,且点为的中点,,.
(1)求证:△;
(2)判断与的位置关系,并说明理由.
22.如图,为线段上一点,,,.
(1)求证:;
(2)若,,求的度数.
23.倍长中线法与作平行线是构造全等三角形常见的辅助线.
(1)如图1,在中,,中线,求的取值范围.方法一:延长到E使,连接;方法二:过点C作的平行线交的延长线于E.请你从以上两种方法中选一种方法证明,并直接写出的取值范围;
(2)如图2,在中,点B、D在上,,点D是的中点,若平分,求证:.
24.在和中,,,,连接,.
【发现问题】如图①,若,延长交点D,则与的数量关系是_________,的度数为_________.
【类比探究】如图②,若,延长,相交于点D,请猜想与的数量关系及的度数,并说明理由.
【拓展延伸】如图③,若,且点B,E,F在同一条直线上,过点A作,垂足为点M,请猜想,,之间的数量关系,并说明理由.
答案:
一、单选题
1.C
【分析】窗框与钉上的木条形成三角形,是利用三角形稳定性;张开的梯腿地面形成三角形,是利用三角形稳定性;伸缩门的结构是平行四边形,不是利用三角形稳定性;张开的马扎腿形成三角形,是利用三角形稳定性.
解:A、木窗框与对角钉的木条形成的三角形,三边和三角固定,防止安装变形,是利用三角形的稳定性;
B、活动梯子,张开的梯腿与地面形成三角形,三边和三角固定,防止登上变形,是利用三角形的稳定性;
C、伸缩门的结构是平行四边形,四角活动可以变形开关门,是利用四边形的不稳定性,不是利用三角形的稳定性;
D、小马扎的座面与张开的马扎腿形成三角形,三边与三角固定,防止坐上变形,是利用三角形的稳定性.
故选:C.
2.A
【分析】根据角平分线的作图方法解答即可.
解:根据角平分线的作法可知,OM=ON,CM=CN,
又∵OC是公共边,
∴△OMC≌△ONC的根据是“SSS”.
故选A.
3.D
【分析】先利用SSS证明,利用全等三角形的性质推出,连接AO,延长至F,利用三角形外角的性质可得,由此可解.
解:∵AB=AC,BD=EC,
∴,即,
在和中,
,
∴,
∴,
如图,连接AO,延长AO至F,
根据三角形外角的性质可得,,,
∴,
故选:D.
4.D
【分析】本题考查了全等三角形的判定.将各个选项依次代入题目当中,再根据全等三角形的判定方法依次判断即可.一般三角形全等的判定方法有、、、,注意没有.熟练掌握全等三角形的判定方法是解题的关键.
解:A、若添加,则可根据证明,故A选项不符合题意;
B、若添加,则可得,则可根据证明,故B选项不符合题意;
C、若添加,则可根据证明,故C选项不符合题意;
D、若添加,则成了,不能证明,故D选项符合题意.
故选:D
5.A
【分析】利用,,∠C=∠M=54°证明与全等,利用全等三角形的性质可得到答案.
解:在与中,
所以:
所以B,C,D,都错误,A正确.
故选A.
6.D
【分析】本题考查了全等三角形的判定与性质,三角形三边关系,在延长线上截取,连接,证明△ADC≌△EDB,得到,在中,根据三角形三边关系得到,即可得到.
解:如图,在延长线上截取,连接.
∵点是边上的中点,
∴,
在和中,
,
∴△ADC≌△EDB,
∴,
∴在中,
∵,
∴,
∴,
即.
故选:D
7.B
【分析】根据题意应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、2块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第3块有完整的两角及夹边,符合,满足题目要求的条件,是符合题意的,
故选:B.
8.C
【分析】考查了全等三角形的判定和性质,三角形内角和定理等知识,解题的关键是准确寻找全等三角形解决问题.
先证明,进而得到角的关系,再由的度数进行转化,最后利用三角形的内角和即可得到答案.
解:∵等腰直角
∴,,
∴,
∴,
∵等腰直角
∴,,
,
∴∠BCE+∠ACE=∠ACD+∠ACE,
,
在和中,
,
,
,
,
,
.
故选:C.
9.C
【分析】本题考查网格中的全等三角形,会利用全等图形求正方形网格中角度之和是解答的关键.根据网格特点,可得出,进而可求解.
解:如图,
由图可知:,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故选C.
10.B
【分析】证明,由全等三角形的性质可得出.由图形的面积可得出③④正确.
解:∵,,
∴.
∵,,,
∴,故①正确;
∴.
∵,
∴.
∵,
∴,
故②正确;
∵,,
∴四边形的面积是;
故③错误;
∵,
∴
∴.
故④正确.
综上所述,正确的是①②④;
故选:B.
二、填空题
11.SSS
【分析】根据SSS证明三角形全等即可解答.
解:在和△中,
,
.
故答案为:.
12.105
【分析】本题考查邻补角定义,全等三角形性质及判定.根据题意可证,继而得到,再利用邻补角定义计算度数即可.
解:在和中,
,
∴,
∵,
∴,
∴,
故答案为:105.
13.55
【分析】根据SAS证明△ACE≌△DCE,根据全等三角形的性质可得∠CDE=∠A=100°,再根据三角形外角的性质可求∠BED.
解:∵CE平分∠ACB,
∴∠ACE=∠DCE,
在△ACE与△DCE中,
,
∴△ACE≌△DCE(SAS),
∴∠CDE=∠A=100°,
∵∠B=45°,
∴∠BED=∠CDE﹣∠B=100°﹣45°=55°.
故答案为:55.
14.
【分析】本题考查了全等三角形的判定和性质,连接,证明,可得,再证明,即可得到,掌握全等三角形的判定和性质是解题的关键.
解:连接,
∵,
∴,
∴,
在和中,
,
∴,
∴,
故答案为:.
15.3.2
解:如图,在BC上截取BE=AB,
则CE=BC BE=7.6 4.4=3.2,
∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SAS),
∴AD=DE,∠BED=∠A,
∵∠BAC=2∠C,∠BED=∠C+∠CDE,
∴∠C=∠CDE,
∴CE=DE=BC AB=3.2,
∴AD=DE=3.2,
故答案为3.2.
16.16
【分析】此题主要考查了全等三角形的判定和性质,作出辅助线,根据证明全等,是解题的关键.
根据证明与全等,,然后利用代数求解即可.
解:∵是高,
∴,
∵,
∴,
在上截取,如图所示:
在与中
,
∴,
∴,
∴.
故答案为:16.
17.
【分析】本题考查了全等三角形的判定与性质;首先证明可得,然后根据直角三角形两个锐角互余可得,进而可以解决问题.
解:、分别是、两边上的高,
,
,,
,
在和中
,
,
,
,,
,
,,
,
即,
故答案为:.
18.3
【分析】本题主要考查了全等三角形的判定及性质,垂线段的性质,正确作出辅助线是解题的关键.在上截取,证明,可得,根据垂线段最短的性质,即可得到时,取最小值,根据三角形面积公式即可解答.
解:如图,在上截取,
平分,
,
在与中,
,
,
,
,
∵垂线段最短,
∴当时,取最小值,如图所示:
∵,,
∴,
∵,
∴,
解得:,
的最小值为3,
故答案为:3.
三、解答题
19.
解:(1)在和中
,
∴,
∴;
(2)∵,
∴,
在和 CAF中
,
∴,
∴.
20.
解:(1)证明:∵,
∴,
即,
在和中,
,
∴.
(2)∵,
∴,
∴,
在 ADE和 CBF中,
,
∴,
∴,
∴.
21.
解:(1)证明:点为的中点,
,
在和中,
,
.
(2)解:,
理由:,
,
.
22.
解:(1)证明:∵,
∴.
在和中,
∵,
∴;
(2)解:由(1)得,
又∵,
∴,,
∴,
∴的度数为.
23.
(1)解:选方法一来证明,
是的中线,
在和中
,
,
在中,
,
,
即:,
,
(2)解:延长到F使,连接,如图所示;
点D是的中点,
,
在和中,
,
∴△ABD≌△FCD(SAS),
,
平分,
,
,
在和中,
,
,
.
24.
解:,,
理由如下:如图1所示,设与交于点O,
∵,
∴,
即.
∵,,
∴≌,
∴,.
∵,,
∴.
故答案为:,;
,.
理由如下:如图2,
∵,
∴,
即.
∵,,
∴≌,
∴,∠AEB=∠AFC.
∵,,
∴,
∴.
,
理由如下:如图3,
∵,
∴,
即,
∵,,
∴≌,
∴.
∵,,,
∴,即.
∵,
∴.
一、单选题
1.以下生活现象不是利用三角形稳定性的是( )
A. B. C. D.
2.如图是尺规作图法作的平分线时的痕迹图,能判定的理由是( )
A. B. C. D.
3.如图,点E、D分别在AB、AC上,若AB=AC,BE=CD,BD=EC,,,则∠BOC度数是( )
A. B. C. D.
4.如图,在和中,点B、D、C在同一直线上,已知,,添加以下条件后,仍不能判定的是( )
A. B.
C. D.
5.如图,在△ABC与△EMN中,,,∠C=∠M=54°,若∠A=66°,则下列结论正确的是( )
A. B.EN=a C.∠E=60° D.∠N=66°
6.如图,在中,,,点是边上的中点,则的长满足的条件是( )
A. B. C. D.
7.如图,一块三角形的玻璃碎成3块(图中所标1、2、3),小华带第3块碎片去玻璃店,购买形状相同、大小相等的新玻璃,这是利用三角形全等中的( )
A. B. C. D.
8.如图,和都是等腰直角三角形,,则的度数是( )
A. B. C. D.
9.已知,如图所示的网格是由9个相同的小正方形拼成的,图中的各个顶点均为格点,则的度数为( )
A. B. C. D.
10.如图,在四边形ABDE中,,,点C是边BD上一点,,,.下列结论:①;②;③四边形的面积是;④;其中正确的结论个数是( )
A.4 B.3 C.2 D.1
二、填空题
11.数学课上,老师出示如下题目:“已知:.求作:.”如图是小宇用直尺和圆规的作法,其中的道理是作出△,根据全等三角形的性质,得到.△的依据是 .
12.如图,已知,,若,则 度.
13.如图,在△ABC中,D是BC上的一点,CA=CD,CE平分∠ACB,交AB于点E,连接DE,若∠A=100°,∠B=45°,则∠BED= °.
14.如图,是外一点,是上一点,,,,,则的度数为 .
15.如图,△ABC中,∠BAC=2∠C,BD为∠ABC的平分线,BC=7.6,AB=4.4,则AD= .
16.如图,在中,,是高,E是外一点,,连接,,若,,,则的面积为 .
17.如图,在中,,、分别是、边上的高,在上取点,使,在射线上取点,使,连接、,若,,则 .
18.如图,在中,,平分,交于点D,点M、N分别为、上的动点,若,的面积为6,则的最小值为 .
三、解答题
19.已知:如图,,,是的延长线上一点.
求证:
(1);
(2).
20.如图,已知,E、F是上两点,且,,求证:
(1).
(2).
21.如图,的边与的边在一条直线上,且点为的中点,,.
(1)求证:△;
(2)判断与的位置关系,并说明理由.
22.如图,为线段上一点,,,.
(1)求证:;
(2)若,,求的度数.
23.倍长中线法与作平行线是构造全等三角形常见的辅助线.
(1)如图1,在中,,中线,求的取值范围.方法一:延长到E使,连接;方法二:过点C作的平行线交的延长线于E.请你从以上两种方法中选一种方法证明,并直接写出的取值范围;
(2)如图2,在中,点B、D在上,,点D是的中点,若平分,求证:.
24.在和中,,,,连接,.
【发现问题】如图①,若,延长交点D,则与的数量关系是_________,的度数为_________.
【类比探究】如图②,若,延长,相交于点D,请猜想与的数量关系及的度数,并说明理由.
【拓展延伸】如图③,若,且点B,E,F在同一条直线上,过点A作,垂足为点M,请猜想,,之间的数量关系,并说明理由.
答案:
一、单选题
1.C
【分析】窗框与钉上的木条形成三角形,是利用三角形稳定性;张开的梯腿地面形成三角形,是利用三角形稳定性;伸缩门的结构是平行四边形,不是利用三角形稳定性;张开的马扎腿形成三角形,是利用三角形稳定性.
解:A、木窗框与对角钉的木条形成的三角形,三边和三角固定,防止安装变形,是利用三角形的稳定性;
B、活动梯子,张开的梯腿与地面形成三角形,三边和三角固定,防止登上变形,是利用三角形的稳定性;
C、伸缩门的结构是平行四边形,四角活动可以变形开关门,是利用四边形的不稳定性,不是利用三角形的稳定性;
D、小马扎的座面与张开的马扎腿形成三角形,三边与三角固定,防止坐上变形,是利用三角形的稳定性.
故选:C.
2.A
【分析】根据角平分线的作图方法解答即可.
解:根据角平分线的作法可知,OM=ON,CM=CN,
又∵OC是公共边,
∴△OMC≌△ONC的根据是“SSS”.
故选A.
3.D
【分析】先利用SSS证明,利用全等三角形的性质推出,连接AO,延长至F,利用三角形外角的性质可得,由此可解.
解:∵AB=AC,BD=EC,
∴,即,
在和中,
,
∴,
∴,
如图,连接AO,延长AO至F,
根据三角形外角的性质可得,,,
∴,
故选:D.
4.D
【分析】本题考查了全等三角形的判定.将各个选项依次代入题目当中,再根据全等三角形的判定方法依次判断即可.一般三角形全等的判定方法有、、、,注意没有.熟练掌握全等三角形的判定方法是解题的关键.
解:A、若添加,则可根据证明,故A选项不符合题意;
B、若添加,则可得,则可根据证明,故B选项不符合题意;
C、若添加,则可根据证明,故C选项不符合题意;
D、若添加,则成了,不能证明,故D选项符合题意.
故选:D
5.A
【分析】利用,,∠C=∠M=54°证明与全等,利用全等三角形的性质可得到答案.
解:在与中,
所以:
所以B,C,D,都错误,A正确.
故选A.
6.D
【分析】本题考查了全等三角形的判定与性质,三角形三边关系,在延长线上截取,连接,证明△ADC≌△EDB,得到,在中,根据三角形三边关系得到,即可得到.
解:如图,在延长线上截取,连接.
∵点是边上的中点,
∴,
在和中,
,
∴△ADC≌△EDB,
∴,
∴在中,
∵,
∴,
∴,
即.
故选:D
7.B
【分析】根据题意应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、2块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第3块有完整的两角及夹边,符合,满足题目要求的条件,是符合题意的,
故选:B.
8.C
【分析】考查了全等三角形的判定和性质,三角形内角和定理等知识,解题的关键是准确寻找全等三角形解决问题.
先证明,进而得到角的关系,再由的度数进行转化,最后利用三角形的内角和即可得到答案.
解:∵等腰直角
∴,,
∴,
∴,
∵等腰直角
∴,,
,
∴∠BCE+∠ACE=∠ACD+∠ACE,
,
在和中,
,
,
,
,
,
.
故选:C.
9.C
【分析】本题考查网格中的全等三角形,会利用全等图形求正方形网格中角度之和是解答的关键.根据网格特点,可得出,进而可求解.
解:如图,
由图可知:,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
故选C.
10.B
【分析】证明,由全等三角形的性质可得出.由图形的面积可得出③④正确.
解:∵,,
∴.
∵,,,
∴,故①正确;
∴.
∵,
∴.
∵,
∴,
故②正确;
∵,,
∴四边形的面积是;
故③错误;
∵,
∴
∴.
故④正确.
综上所述,正确的是①②④;
故选:B.
二、填空题
11.SSS
【分析】根据SSS证明三角形全等即可解答.
解:在和△中,
,
.
故答案为:.
12.105
【分析】本题考查邻补角定义,全等三角形性质及判定.根据题意可证,继而得到,再利用邻补角定义计算度数即可.
解:在和中,
,
∴,
∵,
∴,
∴,
故答案为:105.
13.55
【分析】根据SAS证明△ACE≌△DCE,根据全等三角形的性质可得∠CDE=∠A=100°,再根据三角形外角的性质可求∠BED.
解:∵CE平分∠ACB,
∴∠ACE=∠DCE,
在△ACE与△DCE中,
,
∴△ACE≌△DCE(SAS),
∴∠CDE=∠A=100°,
∵∠B=45°,
∴∠BED=∠CDE﹣∠B=100°﹣45°=55°.
故答案为:55.
14.
【分析】本题考查了全等三角形的判定和性质,连接,证明,可得,再证明,即可得到,掌握全等三角形的判定和性质是解题的关键.
解:连接,
∵,
∴,
∴,
在和中,
,
∴,
∴,
故答案为:.
15.3.2
解:如图,在BC上截取BE=AB,
则CE=BC BE=7.6 4.4=3.2,
∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SAS),
∴AD=DE,∠BED=∠A,
∵∠BAC=2∠C,∠BED=∠C+∠CDE,
∴∠C=∠CDE,
∴CE=DE=BC AB=3.2,
∴AD=DE=3.2,
故答案为3.2.
16.16
【分析】此题主要考查了全等三角形的判定和性质,作出辅助线,根据证明全等,是解题的关键.
根据证明与全等,,然后利用代数求解即可.
解:∵是高,
∴,
∵,
∴,
在上截取,如图所示:
在与中
,
∴,
∴,
∴.
故答案为:16.
17.
【分析】本题考查了全等三角形的判定与性质;首先证明可得,然后根据直角三角形两个锐角互余可得,进而可以解决问题.
解:、分别是、两边上的高,
,
,,
,
在和中
,
,
,
,,
,
,,
,
即,
故答案为:.
18.3
【分析】本题主要考查了全等三角形的判定及性质,垂线段的性质,正确作出辅助线是解题的关键.在上截取,证明,可得,根据垂线段最短的性质,即可得到时,取最小值,根据三角形面积公式即可解答.
解:如图,在上截取,
平分,
,
在与中,
,
,
,
,
∵垂线段最短,
∴当时,取最小值,如图所示:
∵,,
∴,
∵,
∴,
解得:,
的最小值为3,
故答案为:3.
三、解答题
19.
解:(1)在和中
,
∴,
∴;
(2)∵,
∴,
在和 CAF中
,
∴,
∴.
20.
解:(1)证明:∵,
∴,
即,
在和中,
,
∴.
(2)∵,
∴,
∴,
在 ADE和 CBF中,
,
∴,
∴,
∴.
21.
解:(1)证明:点为的中点,
,
在和中,
,
.
(2)解:,
理由:,
,
.
22.
解:(1)证明:∵,
∴.
在和中,
∵,
∴;
(2)解:由(1)得,
又∵,
∴,,
∴,
∴的度数为.
23.
(1)解:选方法一来证明,
是的中线,
在和中
,
,
在中,
,
,
即:,
,
(2)解:延长到F使,连接,如图所示;
点D是的中点,
,
在和中,
,
∴△ABD≌△FCD(SAS),
,
平分,
,
,
在和中,
,
,
.
24.
解:,,
理由如下:如图1所示,设与交于点O,
∵,
∴,
即.
∵,,
∴≌,
∴,.
∵,,
∴.
故答案为:,;
,.
理由如下:如图2,
∵,
∴,
即.
∵,,
∴≌,
∴,∠AEB=∠AFC.
∵,,
∴,
∴.
,
理由如下:如图3,
∵,
∴,
即,
∵,,
∴≌,
∴.
∵,,,
∴,即.
∵,
∴.
