【沪科版七上同步练习】 第四章 直线与角(基础知识)检测题(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 第四章 直线与角(基础知识)检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 09:26:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】
第四章直线和角(基础知识)检测题
一、单选题
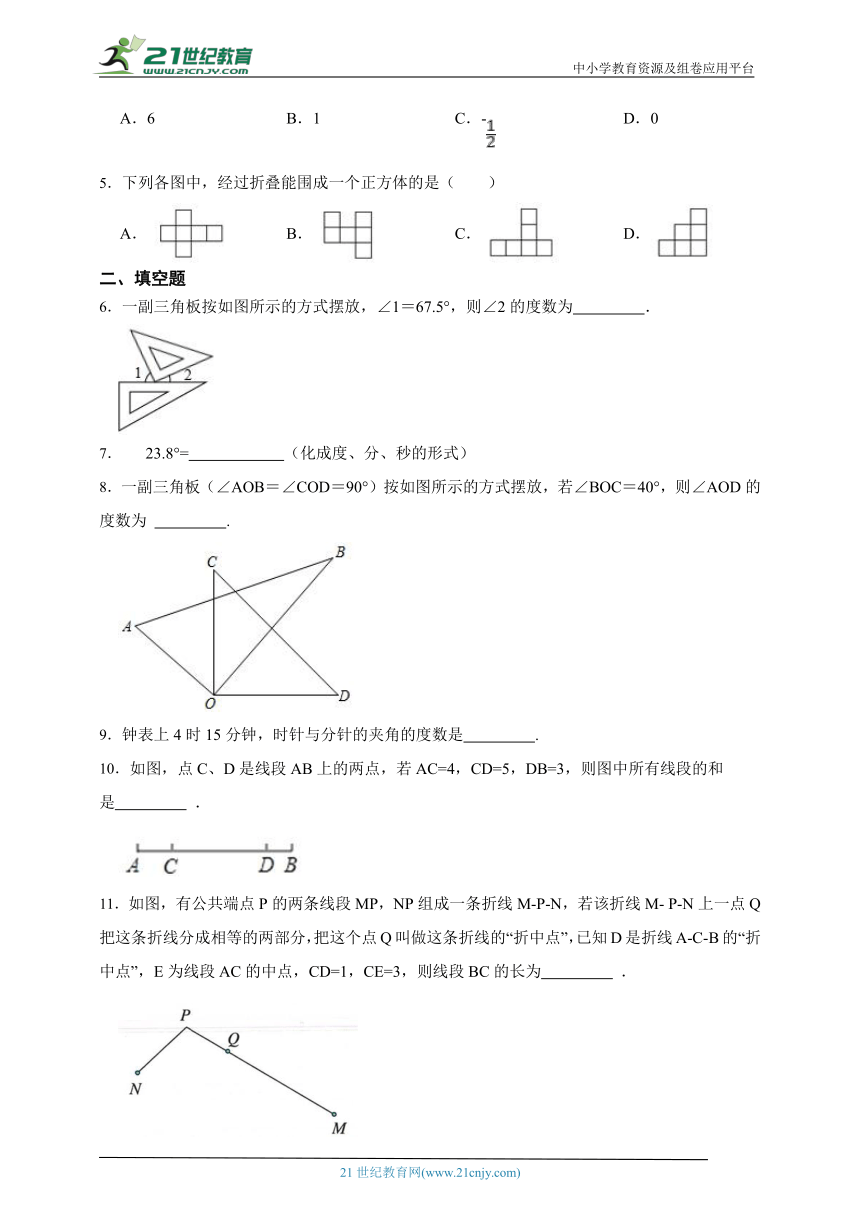
1.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能符合题意解释这一现象的数学知识是:( )
A.两点之间,直段最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
2.如图,下列四个选项中,不是正方体表面展开图的是( )
A. B. C. D.
3.下列图形中,是圆锥侧面展开图的是( )
A. B.
C. D.
4.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面和右面所标数字相等,则x的值是( )
A.6 B.1 C.- D.0
5.下列各图中,经过折叠能围成一个正方体的是( )
A. B. C. D.
二、填空题
6.一副三角板按如图所示的方式摆放,∠1=67.5°,则∠2的度数为 .
7. 23.8°= (化成度、分、秒的形式)
8.一副三角板(∠AOB=∠COD=90°)按如图所示的方式摆放,若∠BOC=40°,则∠AOD的度数为 .
9.钟表上4时15分钟,时针与分针的夹角的度数是 .
10.如图,点C、D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
11.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M- P-N上一点Q把这条折线分成相等的两部分,把这个点Q叫做这条折线的“折中点”,已知D是折线A-C-B的“折中点”,E为线段AC的中点,CD=1,CE=3,则线段BC的长为 .
三、计算题
12.(1)已知,,求,的值.
(2)如果的补角是的余角的3倍.求的度数.
13.计算:
(1)23°53′×3+107°43′÷5;
(2)61°39′-22°5′32″.
四、解答题
14.如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.
15.A,B,C三点在同一条直线上,且线段AB=7cm,点M为线段AB的中点,线段BC=3cm,点N为线段BC的中点,求线段MN的长.
16.如图,点M、N均在数轴上,点M所对应的数是-3,点N在点M的右边,且距M点4个单位长度,点P、Q是数轴上的两个动点.
(1)求出点N所对应的数;
(2)当点P到点M、N的距离之和是5个单位长度时,求出此时点P所对应的数;
(3)若点P、Q分别从点M、N出发,均沿数轴向左运动,点P每秒运动2个单位长度,点Q每秒运动3个单位长度.若点P先出发5秒后点Q出发,当P、Q两点相距2个单位长度时,直接写出此时点P、Q分别对应的数.
五、综合题
17.下图是一正方体的展开图,若正方体相对两个面上的代数式的值相等,求下列代数式的值:
(1)x2+y2;
(2)(x-y)2
18.如图,货轮O航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C.
按下列要求画图并回答问题:
(1)画出线段OB;
(2)画出射线OC;
(3)连接AB交OE于点D;
(4)写出图中∠AOD的所有余角..
19.点 在数轴上分别表示有理数 , 两点之间的距离表示为 ,在数轴上A、B两点之间的距离 .
利用数形结合思想回答下列问题:
(1)数轴上表示-2和1的两点之间的距离是 .
(2)数轴上表示 和-1的两点之间的距离表示为 .
(3)在数轴上点 表示数 ,点 表示数 ,点 表示数 ,且满足 ,若 是数轴上任意一点,点 表示的数是 ,当 时, 的值为多少
六、实践探究题
20.阅读材料,并回答问题:
材料:数学课上,老师给出了如下问题.
如图1,点A、B、C均在直线l上,AB = 8,BC = 2,M是AC的中点,求AM的长.
小明的解答过程如下:
解:如图2,
∵AB = 8,BC = 2,
∴AC = AB-BC = 8-2 = 6.
∵M是AC的中点,
∴ (①).
小芳说:“小明的解答不完整”.
问题:
(1)小明解答过程中的“①”为 ;
(2)你同意小芳的说法吗?如果同意,请将小明的解答过程补充完整;如果不同意,请说明理由.
答案解析部分
1.【答案】C
【知识点】两点之间线段最短
2.【答案】C
【知识点】几何体的展开图
3.【答案】B
【知识点】几何体的展开图
4.【答案】C
【知识点】几何体的展开图
5.【答案】A
【知识点】几何体的展开图
6.【答案】22.5°
【知识点】角的运算
7.【答案】23°48'
【知识点】常用角的度量单位及换算
8.【答案】140°
【知识点】角的运算
9.【答案】
【知识点】钟面角、方位角
10.【答案】41
【知识点】尺规作图的概念
11.【答案】8或4
【知识点】线段的中点;定义新运算;线段的和、差、倍、分的简单计算
12.【答案】(1), (2)
【知识点】余角、补角及其性质
13.【答案】(1)解:93°11′36″
(2)解:39°33′28″
【知识点】常用角的度量单位及换算;角的运算
14.【答案】解:如图所示.
【知识点】立体图形的初步认识
15.【答案】解:①如图,
,
当点C在线段AB的延长线上时,
∵点M是AB的中点,
∴ ,
∵N是BC的中点,
∴ ,
∴MN=BM+BN=3.5+1.5=5cm;
②如图,
,
当点C在线段AB上时,
∵点M是AB的中点,
∴ ,
∵N是BC的中点,
∴ ,
∴MN=BM﹣BN=3.5﹣1.5=2cm,
故线段MN的长为5cm或2cm.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
16.【答案】(1)解:∵点M表示的数是-3,点N在点M的右侧且MN=4,
∴点N所表示的数为-3+4=1,
答:点N所表示的数为1;
(2)解:因为MN=5,因此点P不可能在点M、N之间,
当点P在点M的左侧时,设点P所表示的数为x,则PM=-3-x,PN=1-x,
由PM+PN=5得,-3-x+1-x=5,
解得x=-3.5,
当点P在点N的右侧时,设点P所表示的数为y,则PM=y+3,PN=y-1,
由PM+PN=5得,y+3+y-1=5,
解得y=1.5,
所以当点P到点M,N的距离之和是5个单位时,点P所对应的数是-3.5或1.5;
(3)解:点P,Q对应的数为-37,-35或-45,-47
【知识点】数轴及有理数在数轴上的表示;线段上的两点间的距离
17.【答案】(1)解:x2+y2=(x+y)2-2xy=9+4=13
(2)解:(x-y)2=(x+y)2-4xy=9+8=17
【知识点】代数式求值;几何体的展开图
18.【答案】(1)解:由方向角的定义可以作出
(2)解:由方向角的定义可以作出
(3)解:作线段 , 和 的交点就是 ;如图:
(4)解:由余角的定义可知: 的所有余角是:
【知识点】余角、补角及其性质
19.【答案】(1)3
(2)
(3)解:∵ 且
∴
∴
∴PA= ,PB= ,PC=
∵
∴
根据题意,画出数轴如下:
①当 时,
解得 ,舍去;
②当 时,
解得 ,符合题意;
③ 时,
解得 ,符合题意;
④当 时,
解得 ,舍去.
综上, 的值为 或3.
【知识点】数轴及有理数在数轴上的表示;绝对值及有理数的绝对值;线段上的两点间的距离
20.【答案】(1)中点定义
(2)我同意小芳的说法,将小明的解答补充如下:
如图,∵AB = 8,BC = 2,
∴AC = AB+BC = 8+2 = 10.
∵M是AC的中点,
∴ .
【知识点】线段的中点;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】
第四章直线和角(基础知识)检测题
一、单选题
1.如图,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能符合题意解释这一现象的数学知识是:( )
A.两点之间,直段最短 B.两点确定一条直线
C.两点之间,线段最短 D.经过一点有无数条直线
2.如图,下列四个选项中,不是正方体表面展开图的是( )
A. B. C. D.
3.下列图形中,是圆锥侧面展开图的是( )
A. B.
C. D.
4.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面和右面所标数字相等,则x的值是( )
A.6 B.1 C.- D.0
5.下列各图中,经过折叠能围成一个正方体的是( )
A. B. C. D.
二、填空题
6.一副三角板按如图所示的方式摆放,∠1=67.5°,则∠2的度数为 .
7. 23.8°= (化成度、分、秒的形式)
8.一副三角板(∠AOB=∠COD=90°)按如图所示的方式摆放,若∠BOC=40°,则∠AOD的度数为 .
9.钟表上4时15分钟,时针与分针的夹角的度数是 .
10.如图,点C、D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
11.如图,有公共端点P的两条线段MP,NP组成一条折线M-P-N,若该折线M- P-N上一点Q把这条折线分成相等的两部分,把这个点Q叫做这条折线的“折中点”,已知D是折线A-C-B的“折中点”,E为线段AC的中点,CD=1,CE=3,则线段BC的长为 .
三、计算题
12.(1)已知,,求,的值.
(2)如果的补角是的余角的3倍.求的度数.
13.计算:
(1)23°53′×3+107°43′÷5;
(2)61°39′-22°5′32″.
四、解答题
14.如图,上面一行是一些具体的实物图形,下面一行是一些立体图形,试用线连接立体图形和类似的实物图形.
15.A,B,C三点在同一条直线上,且线段AB=7cm,点M为线段AB的中点,线段BC=3cm,点N为线段BC的中点,求线段MN的长.
16.如图,点M、N均在数轴上,点M所对应的数是-3,点N在点M的右边,且距M点4个单位长度,点P、Q是数轴上的两个动点.
(1)求出点N所对应的数;
(2)当点P到点M、N的距离之和是5个单位长度时,求出此时点P所对应的数;
(3)若点P、Q分别从点M、N出发,均沿数轴向左运动,点P每秒运动2个单位长度,点Q每秒运动3个单位长度.若点P先出发5秒后点Q出发,当P、Q两点相距2个单位长度时,直接写出此时点P、Q分别对应的数.
五、综合题
17.下图是一正方体的展开图,若正方体相对两个面上的代数式的值相等,求下列代数式的值:
(1)x2+y2;
(2)(x-y)2
18.如图,货轮O航行过程中,在它的北偏东60°方向上,与之相距30海里处发现灯塔A,同时在它的南偏东30°方向上,与之相距20海里处发现货轮B,在它的西南方向上发现客轮C.
按下列要求画图并回答问题:
(1)画出线段OB;
(2)画出射线OC;
(3)连接AB交OE于点D;
(4)写出图中∠AOD的所有余角..
19.点 在数轴上分别表示有理数 , 两点之间的距离表示为 ,在数轴上A、B两点之间的距离 .
利用数形结合思想回答下列问题:
(1)数轴上表示-2和1的两点之间的距离是 .
(2)数轴上表示 和-1的两点之间的距离表示为 .
(3)在数轴上点 表示数 ,点 表示数 ,点 表示数 ,且满足 ,若 是数轴上任意一点,点 表示的数是 ,当 时, 的值为多少
六、实践探究题
20.阅读材料,并回答问题:
材料:数学课上,老师给出了如下问题.
如图1,点A、B、C均在直线l上,AB = 8,BC = 2,M是AC的中点,求AM的长.
小明的解答过程如下:
解:如图2,
∵AB = 8,BC = 2,
∴AC = AB-BC = 8-2 = 6.
∵M是AC的中点,
∴ (①).
小芳说:“小明的解答不完整”.
问题:
(1)小明解答过程中的“①”为 ;
(2)你同意小芳的说法吗?如果同意,请将小明的解答过程补充完整;如果不同意,请说明理由.
答案解析部分
1.【答案】C
【知识点】两点之间线段最短
2.【答案】C
【知识点】几何体的展开图
3.【答案】B
【知识点】几何体的展开图
4.【答案】C
【知识点】几何体的展开图
5.【答案】A
【知识点】几何体的展开图
6.【答案】22.5°
【知识点】角的运算
7.【答案】23°48'
【知识点】常用角的度量单位及换算
8.【答案】140°
【知识点】角的运算
9.【答案】
【知识点】钟面角、方位角
10.【答案】41
【知识点】尺规作图的概念
11.【答案】8或4
【知识点】线段的中点;定义新运算;线段的和、差、倍、分的简单计算
12.【答案】(1), (2)
【知识点】余角、补角及其性质
13.【答案】(1)解:93°11′36″
(2)解:39°33′28″
【知识点】常用角的度量单位及换算;角的运算
14.【答案】解:如图所示.
【知识点】立体图形的初步认识
15.【答案】解:①如图,
,
当点C在线段AB的延长线上时,
∵点M是AB的中点,
∴ ,
∵N是BC的中点,
∴ ,
∴MN=BM+BN=3.5+1.5=5cm;
②如图,
,
当点C在线段AB上时,
∵点M是AB的中点,
∴ ,
∵N是BC的中点,
∴ ,
∴MN=BM﹣BN=3.5﹣1.5=2cm,
故线段MN的长为5cm或2cm.
【知识点】线段的中点;线段的和、差、倍、分的简单计算
16.【答案】(1)解:∵点M表示的数是-3,点N在点M的右侧且MN=4,
∴点N所表示的数为-3+4=1,
答:点N所表示的数为1;
(2)解:因为MN=5,因此点P不可能在点M、N之间,
当点P在点M的左侧时,设点P所表示的数为x,则PM=-3-x,PN=1-x,
由PM+PN=5得,-3-x+1-x=5,
解得x=-3.5,
当点P在点N的右侧时,设点P所表示的数为y,则PM=y+3,PN=y-1,
由PM+PN=5得,y+3+y-1=5,
解得y=1.5,
所以当点P到点M,N的距离之和是5个单位时,点P所对应的数是-3.5或1.5;
(3)解:点P,Q对应的数为-37,-35或-45,-47
【知识点】数轴及有理数在数轴上的表示;线段上的两点间的距离
17.【答案】(1)解:x2+y2=(x+y)2-2xy=9+4=13
(2)解:(x-y)2=(x+y)2-4xy=9+8=17
【知识点】代数式求值;几何体的展开图
18.【答案】(1)解:由方向角的定义可以作出
(2)解:由方向角的定义可以作出
(3)解:作线段 , 和 的交点就是 ;如图:
(4)解:由余角的定义可知: 的所有余角是:
【知识点】余角、补角及其性质
19.【答案】(1)3
(2)
(3)解:∵ 且
∴
∴
∴PA= ,PB= ,PC=
∵
∴
根据题意,画出数轴如下:
①当 时,
解得 ,舍去;
②当 时,
解得 ,符合题意;
③ 时,
解得 ,符合题意;
④当 时,
解得 ,舍去.
综上, 的值为 或3.
【知识点】数轴及有理数在数轴上的表示;绝对值及有理数的绝对值;线段上的两点间的距离
20.【答案】(1)中点定义
(2)我同意小芳的说法,将小明的解答补充如下:
如图,∵AB = 8,BC = 2,
∴AC = AB+BC = 8+2 = 10.
∵M是AC的中点,
∴ .
【知识点】线段的中点;线段的和、差、倍、分的简单计算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
