【沪科版七上同步练习】 期末数学试卷一(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 期末数学试卷一(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 18.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-17 20:49:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】 期末试卷一
一、单选题
1.-6的相反数是( )
A.6 B.-6 C. D.
2.计算的结果是( )
A. B.12 C. D.2
3.用四舍五入法取近似数0.05019(精确到0.001)的结果是( )
A.0.05 B.0.050 C.0.0501 D.0.051
4.《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少 设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )
A. B.
C. D.
5.设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列为( )
A.■、▲、● B.■、●、▲ C.▲、●、■ D.▲、■、●
二、填空题
6.数的位置如图,化简 .
7. 在平面直角坐标系中,若点满足,则点A的坐标可以是 (写出一个即可)
8.科学家们测得光在水中的速度约为225000000米/秒,数字225000000用科学记数法表示为 .
9.废旧电池含有少量重金属,随意丢弃会污染环境有资料表明,一粒纽扣大的废旧电池,大约会污染水7.数据7用科学记数法可表示 .
10.在数轴上,与表示-1的点距离为3的点所表示的数是 .
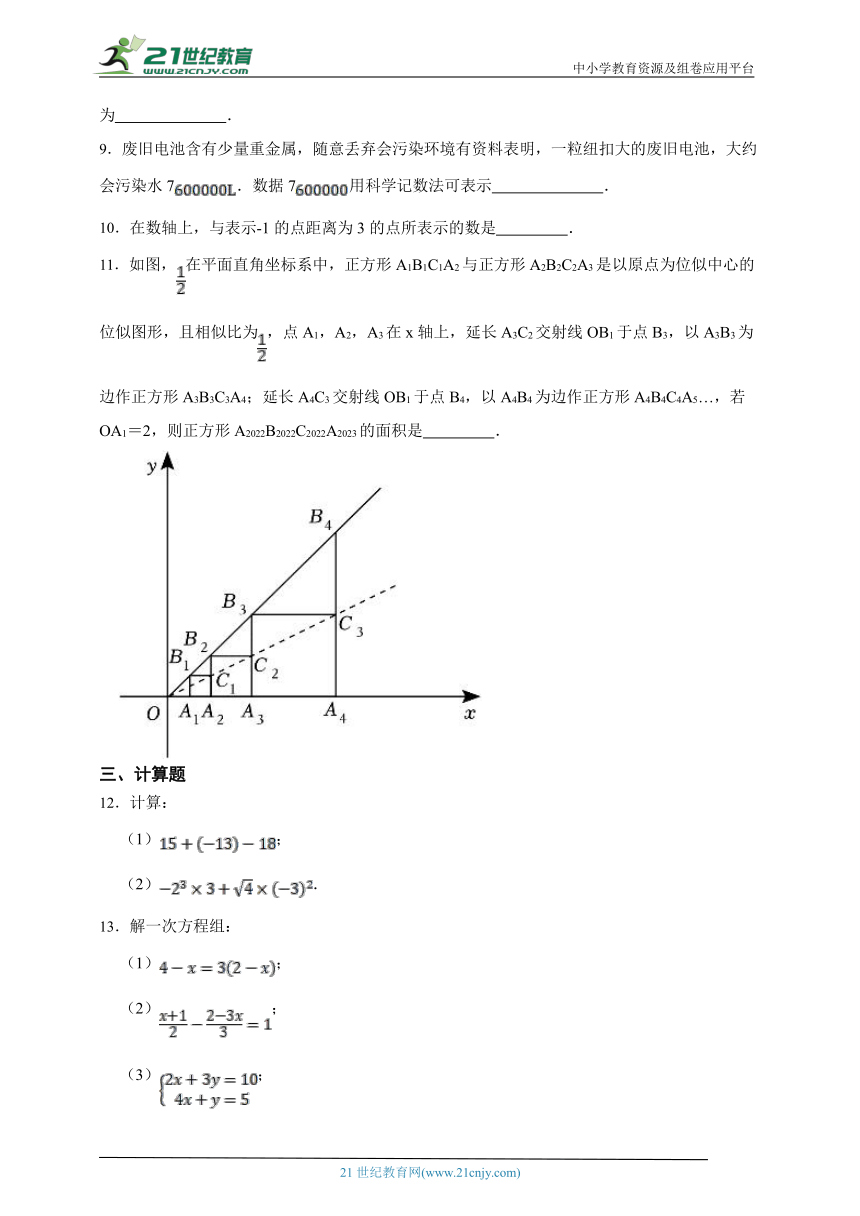
11.如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点为位似中心的位似图形,且相似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边作正方形A4B4C4A5…,若OA1=2,则正方形A2022B2022C2022A2023的面积是 .
三、计算题
12.计算:
(1);
(2).
13.解一次方程组:
(1);
(2);
(3);
(4);
(5);
(6)
14.计算题:
(1)
(2)
四、解答题
15.某校有,,三个课外活动小组,小组有学生名,小组学生人数是小组学生人数的3倍,小组比小组多3名学生,问,,三个课外活动小组共有多少名学生?
16.如图,直线、相交于点O,,平分.
(1)若,求的度数;
(2)若比大24°,求的度数.
17. 根据以下素材,探索完成任务.
如何改造硬纸板制作无盖纸盒?
背景 学校手工社团小组想把一张长50cm,宽40cm的矩形硬纸板,制作成一个高,容积的无盖长方体纸盒,且纸盒的长不小于(纸板的厚度忽略不计).
方案 初始方案:将矩形硬纸板竖着裁剪(阴影部分),剩余纸板的四周各剪去一个同样大小的正方形.
改进方案:将矩形硬纸板竖着裁剪,横着裁剪(阴影部分),剩余纸板的四周各剪去一个同样大小的正方形.
问题解决
任务1 判断方案 请通过计算判断初始方案是否可行?
任务2 改进方案 改进方案中,当时,求x的值.
任务3 探究方案 当裁剪后能制作成符合要求的纸盒时,写出y关于x的函数关系式.
五、综合题
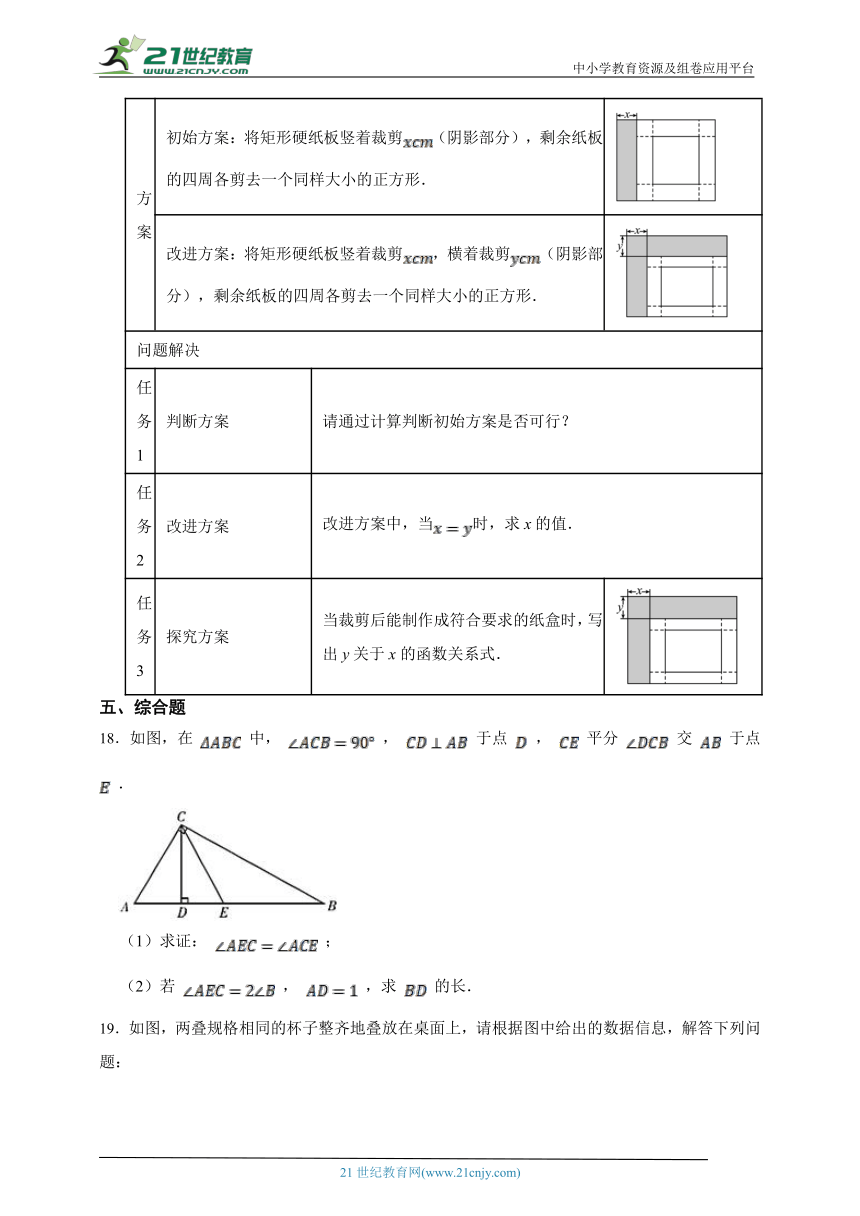
18.如图,在 中, , 于点 , 平分 交 于点 .
(1)求证: ;
(2)若 , ,求 的长.
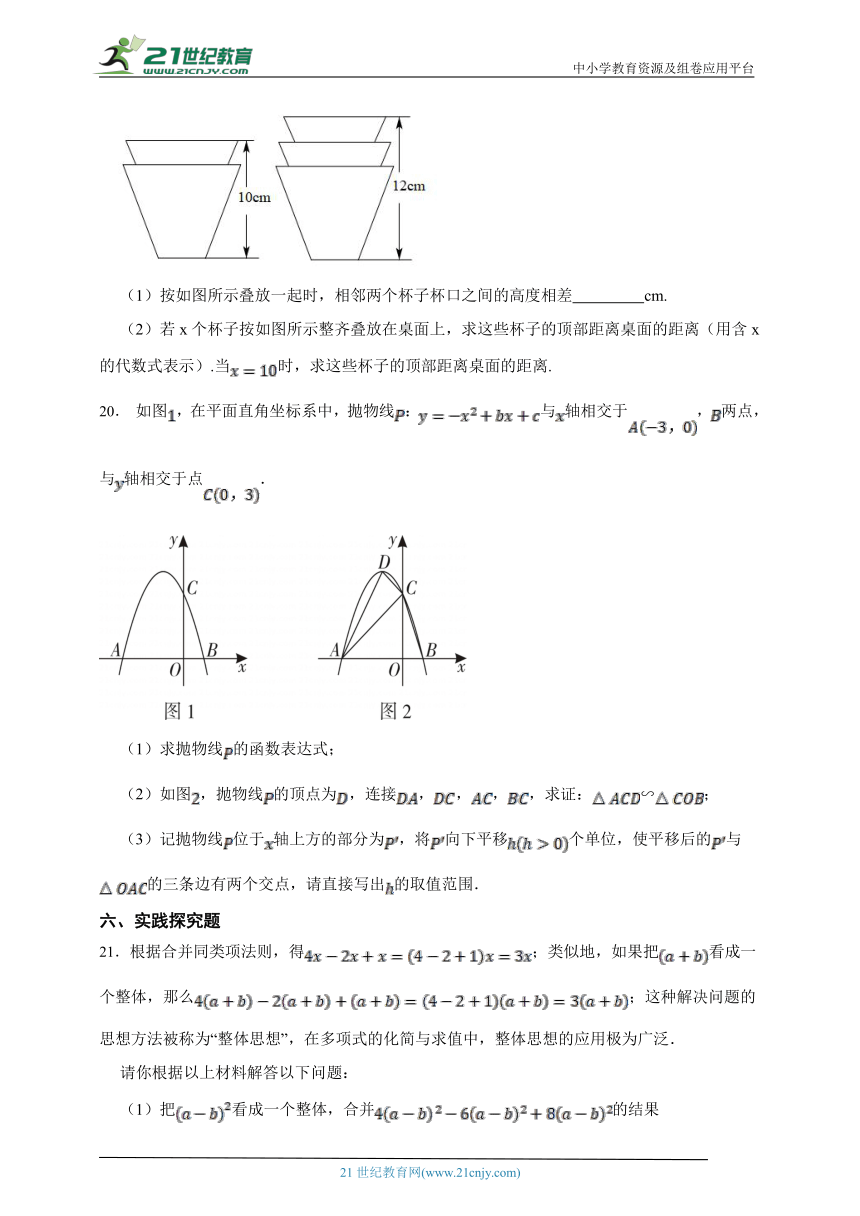
19.如图,两叠规格相同的杯子整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
(1)按如图所示叠放一起时,相邻两个杯子杯口之间的高度相差 cm.
(2)若x个杯子按如图所示整齐叠放在桌面上,求这些杯子的顶部距离桌面的距离(用含x的代数式表示).当时,求这些杯子的顶部距离桌面的距离.
20. 如图,在平面直角坐标系中,抛物线:与轴相交于,两点,与轴相交于点.
(1)求抛物线的函数表达式;
(2)如图,抛物线的顶点为,连接,,,,求证:∽;
(3)记抛物线位于轴上方的部分为,将向下平移个单位,使平移后的与的三条边有两个交点,请直接写出的取值范围.
六、实践探究题
21.根据合并同类项法则,得;类似地,如果把看成一个整体,那么;这种解决问题的思想方法被称为“整体思想”,在多项式的化简与求值中,整体思想的应用极为广泛.
请你根据以上材料解答以下问题:
(1)把看成一个整体,合并的结果是 ;
(2)已知,求的值;
(3)已知,,,求的值.
答案解析部分
1.【答案】A
【知识点】相反数及有理数的相反数
2.【答案】C
【知识点】有理数的减法法则
3.【答案】B
【知识点】近似数及有效数字
4.【答案】C
【知识点】二元一次方程组的应用-古代数学问题
5.【答案】A
【知识点】等式的基本性质;不等式的性质
6.【答案】4
【知识点】有理数的加、减混合运算;绝对值的非负性
7.【答案】(1,1)(答案不唯一)
【知识点】有理数的乘法法则;点的坐标与象限的关系;不等式的性质
8.【答案】2.25×108
【知识点】科学记数法表示大于10的数
9.【答案】7.6×
【知识点】科学记数法表示大于10的数
10.【答案】2或-4
【知识点】数轴及有理数在数轴上的表示
11.【答案】
【知识点】正方形的性质;相似三角形的判定与性质;位似变换;探索图形规律;用代数式表示图形变化规律
12.【答案】(1)解:
;
(2)解:
.
【知识点】有理数的加、减混合运算;有理数混合运算法则(含乘方)
13.【答案】(1)解:去括号,得,
移项,得,
合并同类项,得,
系数化为1,得;
(2)解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得;
(3)解:,
,得,
解得,
把代入①,得,
解得,
∴方程组的解为;
(4)解:,
,得,
解得,
把代入①,得,
解得,
∴方程组的解为;
(5)解:原方程组变形为,
,得,
把代入②,得,
解得,
∴原方程组的解为;
(6)解:原方程组变形为,
,得,
解得,
把代入①,得,
解得,
∴原方程组的解为.
【知识点】解一元一次方程;解二元一次方程组
14.【答案】(1)解:
=
=0
(2)解:
=
=
=-9
【知识点】绝对值及有理数的绝对值;有理数的加、减混合运算;有理数混合运算法则(含乘方)
15.【答案】解:小组有学生名,小组学生人数是小组学生人数的3倍,
小组学生人数为名,
小组比小组多3名学生,小组学生人数为名,
,,三个课外活动小组共有名.
答:,,三个课外活动小组共有名学生
【知识点】整式的加减运算
16.【答案】(1)解:,,
平分,,
,,
的度数为56°;
(2)解:设,比大24°,
平分,,
,,
,解得:
,,
的度数为142°.
【知识点】垂线的概念;对顶角及其性质;邻补角;角平分线的概念
17.【答案】解:任务1:根据题意得:,解得:,
此时长方体盒子的长为:<32cm
∴初始方案是不可行;
任务2:当时,根据题意得:,
解得:或,
当时,盒子的长为,符合题意;
当时,盒子的长为,不符合题意;
∴x的值为4;
任务3:,
【知识点】一元一次方程的实际应用-几何问题;一元二次方程的应用-几何问题
18.【答案】(1)解:∵ , ,
∴ ,
∴ .
∵ 平分 ,
∴ ,
∴ ,
即 .
(2)解:∵ , ,
∴ .
又∵ , ,
∴ .
又∵ ,
∴ , .
∴ 中, ,
∴ 中, ,
∴ .
【知识点】角平分线的性质;含30°角的直角三角形;角平分线的概念
19.【答案】(1)2
(2)解:一个杯子的高度为:cm,
每增加一个杯子,所叠杯子的总高度增加,
故杯子的顶部距离桌面的距离为:,
将代入中得:(cm),
故这些杯子的顶部距离桌面的距离为.
【知识点】列式表示数量关系;利用整式的加减运算化简求值
20.【答案】(1)解:把、分别代入,得:
,
解得:,
抛物线的函数表达式为;
(2)解:证明:,
点,
令,
解得:,,
点坐标为
,,
,,
,
,
,
,
,,,
,
∽;
(3)
【知识点】待定系数法求二次函数解析式;线段上的两点间的距离;平移的性质;相似三角形的判定;二次函数与一次函数的综合应用
21.【答案】(1)
(2)解:∵,
∴,
(3)解:∵,,,
∴,
,
【知识点】代数式求值;合并同类项法则及应用
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】 期末试卷一
一、单选题
1.-6的相反数是( )
A.6 B.-6 C. D.
2.计算的结果是( )
A. B.12 C. D.2
3.用四舍五入法取近似数0.05019(精确到0.001)的结果是( )
A.0.05 B.0.050 C.0.0501 D.0.051
4.《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少 设一只 雀的重量为x斤,一只燕的重量为y斤,则可列方程组为( )
A. B.
C. D.
5.设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,那么●、▲、■这三种物体按质量从大到小的顺序排列为( )
A.■、▲、● B.■、●、▲ C.▲、●、■ D.▲、■、●
二、填空题
6.数的位置如图,化简 .
7. 在平面直角坐标系中,若点满足,则点A的坐标可以是 (写出一个即可)
8.科学家们测得光在水中的速度约为225000000米/秒,数字225000000用科学记数法表示为 .
9.废旧电池含有少量重金属,随意丢弃会污染环境有资料表明,一粒纽扣大的废旧电池,大约会污染水7.数据7用科学记数法可表示 .
10.在数轴上,与表示-1的点距离为3的点所表示的数是 .
11.如图,在平面直角坐标系中,正方形A1B1C1A2与正方形A2B2C2A3是以原点为位似中心的位似图形,且相似比为,点A1,A2,A3在x轴上,延长A3C2交射线OB1于点B3,以A3B3为边作正方形A3B3C3A4;延长A4C3交射线OB1于点B4,以A4B4为边作正方形A4B4C4A5…,若OA1=2,则正方形A2022B2022C2022A2023的面积是 .
三、计算题
12.计算:
(1);
(2).
13.解一次方程组:
(1);
(2);
(3);
(4);
(5);
(6)
14.计算题:
(1)
(2)
四、解答题
15.某校有,,三个课外活动小组,小组有学生名,小组学生人数是小组学生人数的3倍,小组比小组多3名学生,问,,三个课外活动小组共有多少名学生?
16.如图,直线、相交于点O,,平分.
(1)若,求的度数;
(2)若比大24°,求的度数.
17. 根据以下素材,探索完成任务.
如何改造硬纸板制作无盖纸盒?
背景 学校手工社团小组想把一张长50cm,宽40cm的矩形硬纸板,制作成一个高,容积的无盖长方体纸盒,且纸盒的长不小于(纸板的厚度忽略不计).
方案 初始方案:将矩形硬纸板竖着裁剪(阴影部分),剩余纸板的四周各剪去一个同样大小的正方形.
改进方案:将矩形硬纸板竖着裁剪,横着裁剪(阴影部分),剩余纸板的四周各剪去一个同样大小的正方形.
问题解决
任务1 判断方案 请通过计算判断初始方案是否可行?
任务2 改进方案 改进方案中,当时,求x的值.
任务3 探究方案 当裁剪后能制作成符合要求的纸盒时,写出y关于x的函数关系式.
五、综合题
18.如图,在 中, , 于点 , 平分 交 于点 .
(1)求证: ;
(2)若 , ,求 的长.
19.如图,两叠规格相同的杯子整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
(1)按如图所示叠放一起时,相邻两个杯子杯口之间的高度相差 cm.
(2)若x个杯子按如图所示整齐叠放在桌面上,求这些杯子的顶部距离桌面的距离(用含x的代数式表示).当时,求这些杯子的顶部距离桌面的距离.
20. 如图,在平面直角坐标系中,抛物线:与轴相交于,两点,与轴相交于点.
(1)求抛物线的函数表达式;
(2)如图,抛物线的顶点为,连接,,,,求证:∽;
(3)记抛物线位于轴上方的部分为,将向下平移个单位,使平移后的与的三条边有两个交点,请直接写出的取值范围.
六、实践探究题
21.根据合并同类项法则,得;类似地,如果把看成一个整体,那么;这种解决问题的思想方法被称为“整体思想”,在多项式的化简与求值中,整体思想的应用极为广泛.
请你根据以上材料解答以下问题:
(1)把看成一个整体,合并的结果是 ;
(2)已知,求的值;
(3)已知,,,求的值.
答案解析部分
1.【答案】A
【知识点】相反数及有理数的相反数
2.【答案】C
【知识点】有理数的减法法则
3.【答案】B
【知识点】近似数及有效数字
4.【答案】C
【知识点】二元一次方程组的应用-古代数学问题
5.【答案】A
【知识点】等式的基本性质;不等式的性质
6.【答案】4
【知识点】有理数的加、减混合运算;绝对值的非负性
7.【答案】(1,1)(答案不唯一)
【知识点】有理数的乘法法则;点的坐标与象限的关系;不等式的性质
8.【答案】2.25×108
【知识点】科学记数法表示大于10的数
9.【答案】7.6×
【知识点】科学记数法表示大于10的数
10.【答案】2或-4
【知识点】数轴及有理数在数轴上的表示
11.【答案】
【知识点】正方形的性质;相似三角形的判定与性质;位似变换;探索图形规律;用代数式表示图形变化规律
12.【答案】(1)解:
;
(2)解:
.
【知识点】有理数的加、减混合运算;有理数混合运算法则(含乘方)
13.【答案】(1)解:去括号,得,
移项,得,
合并同类项,得,
系数化为1,得;
(2)解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为1,得;
(3)解:,
,得,
解得,
把代入①,得,
解得,
∴方程组的解为;
(4)解:,
,得,
解得,
把代入①,得,
解得,
∴方程组的解为;
(5)解:原方程组变形为,
,得,
把代入②,得,
解得,
∴原方程组的解为;
(6)解:原方程组变形为,
,得,
解得,
把代入①,得,
解得,
∴原方程组的解为.
【知识点】解一元一次方程;解二元一次方程组
14.【答案】(1)解:
=
=0
(2)解:
=
=
=-9
【知识点】绝对值及有理数的绝对值;有理数的加、减混合运算;有理数混合运算法则(含乘方)
15.【答案】解:小组有学生名,小组学生人数是小组学生人数的3倍,
小组学生人数为名,
小组比小组多3名学生,小组学生人数为名,
,,三个课外活动小组共有名.
答:,,三个课外活动小组共有名学生
【知识点】整式的加减运算
16.【答案】(1)解:,,
平分,,
,,
的度数为56°;
(2)解:设,比大24°,
平分,,
,,
,解得:
,,
的度数为142°.
【知识点】垂线的概念;对顶角及其性质;邻补角;角平分线的概念
17.【答案】解:任务1:根据题意得:,解得:,
此时长方体盒子的长为:<32cm
∴初始方案是不可行;
任务2:当时,根据题意得:,
解得:或,
当时,盒子的长为,符合题意;
当时,盒子的长为,不符合题意;
∴x的值为4;
任务3:,
【知识点】一元一次方程的实际应用-几何问题;一元二次方程的应用-几何问题
18.【答案】(1)解:∵ , ,
∴ ,
∴ .
∵ 平分 ,
∴ ,
∴ ,
即 .
(2)解:∵ , ,
∴ .
又∵ , ,
∴ .
又∵ ,
∴ , .
∴ 中, ,
∴ 中, ,
∴ .
【知识点】角平分线的性质;含30°角的直角三角形;角平分线的概念
19.【答案】(1)2
(2)解:一个杯子的高度为:cm,
每增加一个杯子,所叠杯子的总高度增加,
故杯子的顶部距离桌面的距离为:,
将代入中得:(cm),
故这些杯子的顶部距离桌面的距离为.
【知识点】列式表示数量关系;利用整式的加减运算化简求值
20.【答案】(1)解:把、分别代入,得:
,
解得:,
抛物线的函数表达式为;
(2)解:证明:,
点,
令,
解得:,,
点坐标为
,,
,,
,
,
,
,
,,,
,
∽;
(3)
【知识点】待定系数法求二次函数解析式;线段上的两点间的距离;平移的性质;相似三角形的判定;二次函数与一次函数的综合应用
21.【答案】(1)
(2)解:∵,
∴,
(3)解:∵,,,
∴,
,
【知识点】代数式求值;合并同类项法则及应用
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
