人教版数学八年级下册17.1勾股定理作业(含解析)
文档属性
| 名称 | 人教版数学八年级下册17.1勾股定理作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 06:08:29 | ||
图片预览


文档简介
初中数学17.1勾股定理作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
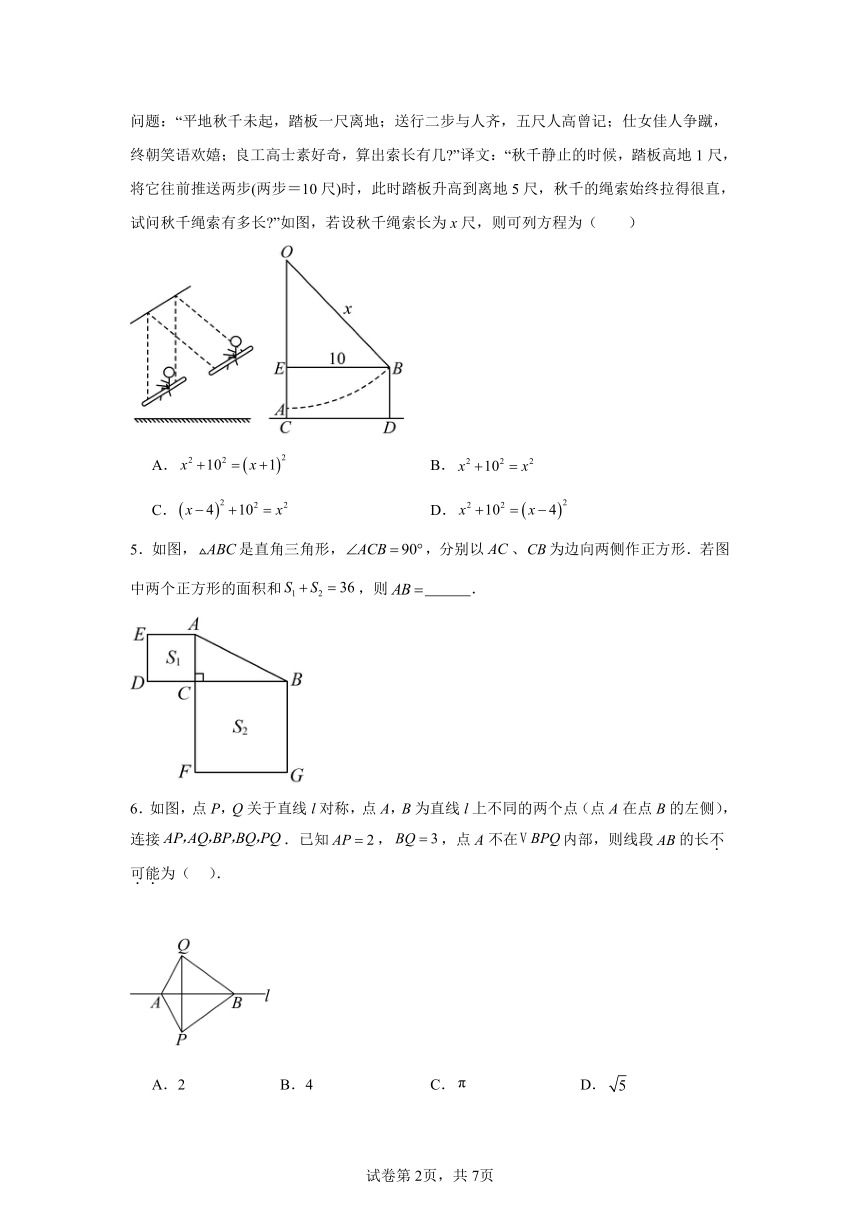
1.如图,在中,,以点为圆心,长为半径作弧,交于点,再分别以,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点.若,,则的长为( )
A. B. C.4 D.
2.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是( )
A.7 B. C. D.
3.如图,平行四边形的对角线,相交于点,且,点为边上一动点(不与点A,重合),于点,于点,若,,则的最小值为( )
A.3 B.2 C. D.
4.《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几 ”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长 ”如图,若设秋千绳索长为x尺,则可列方程为( )
A. B.
C. D.
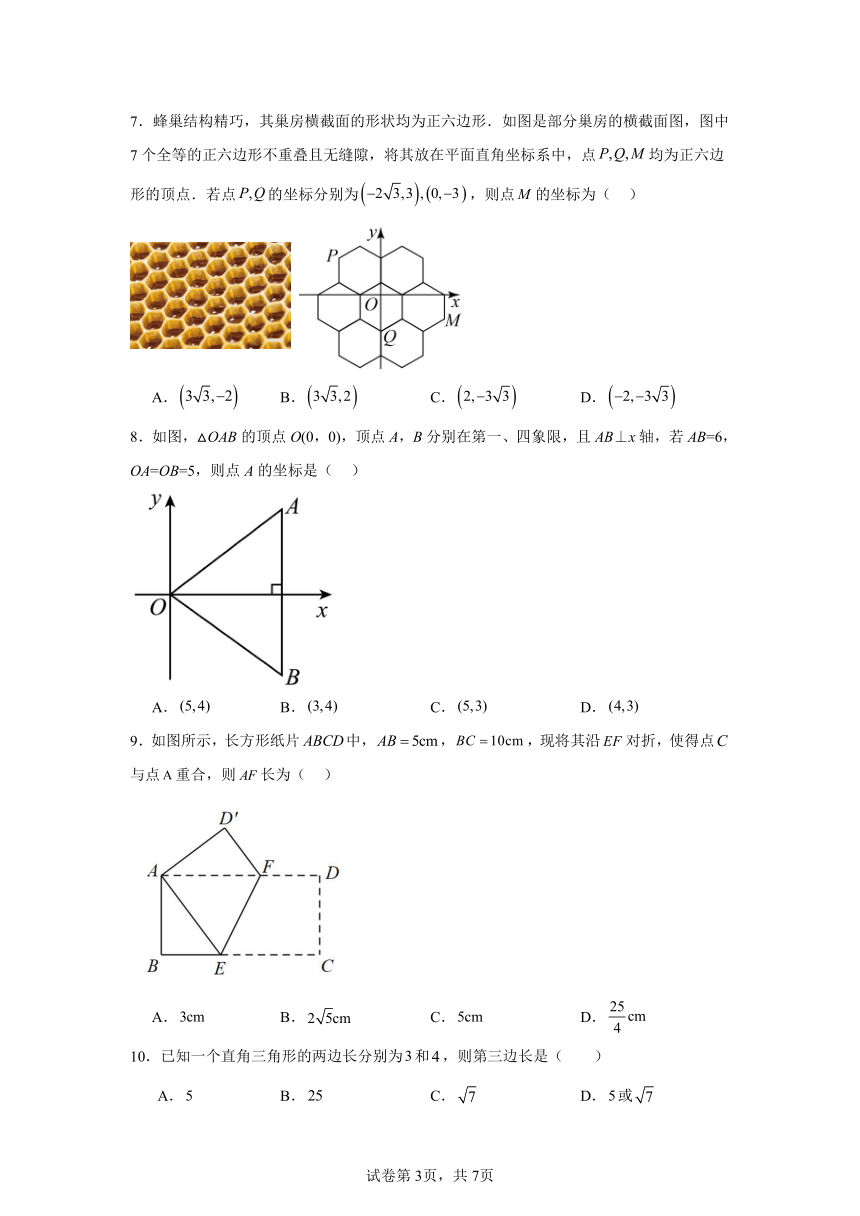
5.如图,是直角三角形,,分别以、为边向两侧作正方形.若图中两个正方形的面积和,则 .
6.如图,点P,Q关于直线l对称,点A,B为直线l上不同的两个点(点A在点B的左侧),连接.已知,,点A不在内部,则线段的长不可能为( ).
A.2 B.4 C. D.
7.蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为,则点的坐标为( )
A. B. C. D.
8.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A. B. C. D.
9.如图所示,长方形纸片中,,,现将其沿对折,使得点与点重合,则长为( )
A. B. C. D.
10.已知一个直角三角形的两边长分别为和,则第三边长是( )
A. B. C. D.或
二、填空题
11.已知直角三角形的两边长分别为3、4.则第三边长为 .
12.如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
(1)线段的长为 ;
(2)若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .
13.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3 dm、2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 dm.
14.如图,在中,,点在边上.将沿折叠,使点落在点处,连接,则的最小值为 .
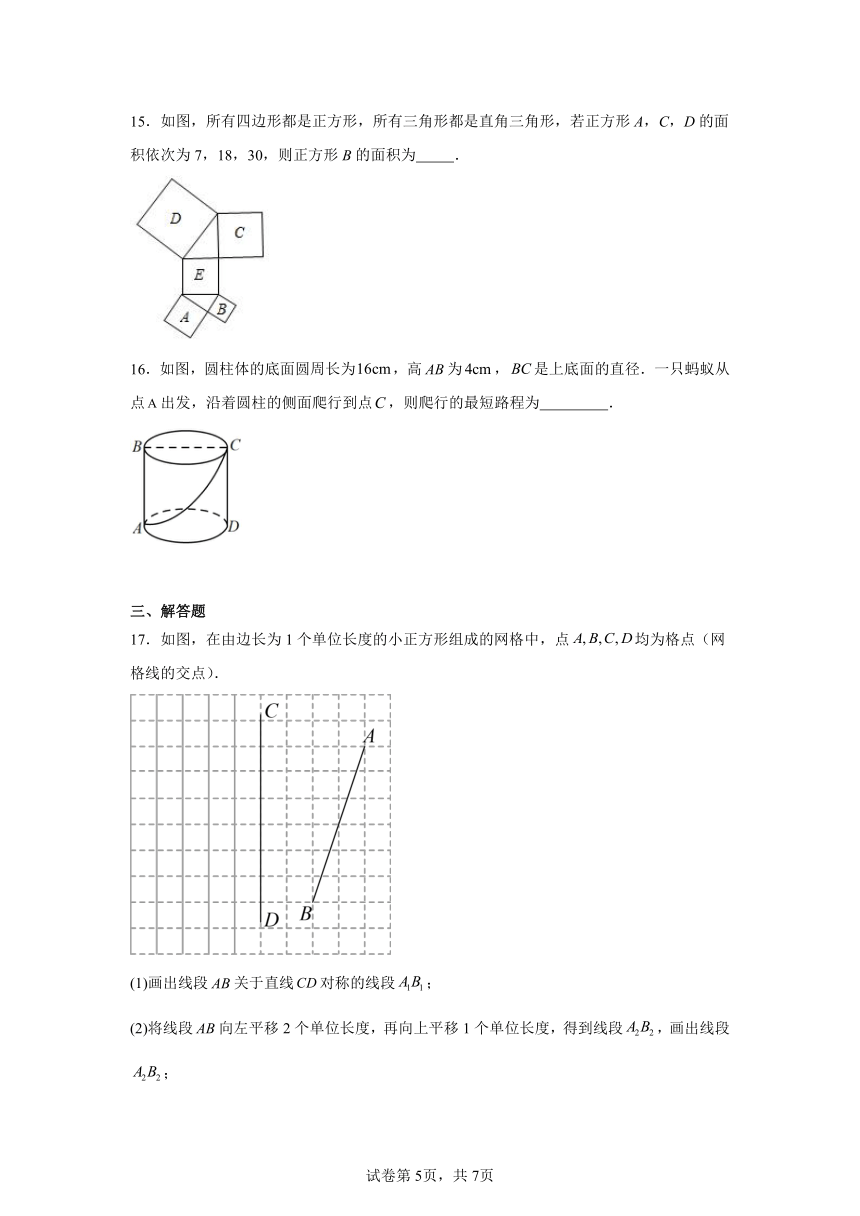
15.如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为7,18,30,则正方形B的面积为 .
16.如图,圆柱体的底面圆周长为,高为,是上底面的直径.一只蚂蚁从点出发,沿着圆柱的侧面爬行到点,则爬行的最短路程为 .
三、解答题
17.如图,在由边长为1个单位长度的小正方形组成的网格中,点均为格点(网格线的交点).
(1)画出线段关于直线对称的线段;
(2)将线段向左平移2个单位长度,再向上平移1个单位长度,得到线段,画出线段;
(3)描出线段上的点及直线上的点,使得直线垂直平分.
18.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即ab×4+(b-a)2,从而得到等式c2=ab×4+(b-a)2,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题:
如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
19.如图,在四边形中,点E是边上一点,且,.
求证:;
若,时,求的面积.
20.如图,.
写出与的数量关系
延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了作图-复杂作图、勾股定理,解决本题的关键是熟练掌握线段垂直平分线的性质.根据作图过程可得是的垂直平分线,根据勾股定理可得的长,再根据等面积法即可求出的长.
【详解】解:在中,,,,
,
由作图知,,
,
,
故选:D.
2.B
【分析】作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.本题考查的是平面展开最短路径问题,熟知此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.
【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是6和3,
则所走的最短线段是;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是5和4,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是7和2,
所以走的最短线段是;
三种情况比较而言,第二种情况最短.
∵
∴它需要爬行的最短路线的长是,
故选:B.
3.C
【分析】本题考查了矩形的判定和性质,垂线段最短,勾股定理,先根据勾股定理计算出,再证明四边形是矩形,得到,再根据垂线段最短求出的最小值即可.
【详解】解:如下图所示,连接,
∵,且四边形是平行四边形,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
∴当最小时,最小,
当时,当最小,
当时,,
∴,
故选:C.
4.C
【分析】此题主要考查了考差了勾股定理的应用,关键是正确理解题意,表示出 的长,掌握直角三角形中两直角边的平方和等于斜边的平方.设秋千的绳索长为 尺,根据题意可得尺,利用勾股定理可得方程.
【详解】解:设秋千的绳索长为 尺,根据题意可列方程为:即.
故选:C
5.6
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
根据勾股定理即可求解.
【详解】解:在中,由勾股定理得,,
∵,,,
∴,
故答案为:6.
6.A
【分析】本题考查轴对称的性质,勾股定理,实数大小比较.
先根据轴对称的性质,得,再求出当时 ,,然后由点A不在内部,得出,最后由,即可得出答案.
【详解】解:当时 ,
∵点P,Q关于直线l对称,点A,B为直线l上不同的两个点,
∴,,
∵
∴,
由勾股定理,得
∵点A不在内部,
∴
∵
∴的长不可能为2,
故选:A.
7.A
【分析】连接,设正六边形的边长为a,由正六边形的性质及点P的坐标可求得a的值,即可求得点M的坐标.
【详解】解:连接,如图,设正六边形的边长为a,
∵,
∴,
∵,
∴,
∴,
∴,,
∵点P的坐标为,
∴,
即;
∴,,
∴点M的坐标为.
故选:A.
【点睛】本题考查了坐标与图形,正六边形的性质,勾股定理,含30度角直角三角形的性质等知识,掌握这些知识是解题的关键.
8.D
【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.
【详解】解:∵AB⊥x轴,
∴∠ACO=∠BCO=90°,
∵OA=OB,OC=OC,
∴△ACO≌△BCO(HL),
∴AC=BC=AB=3,
∵OA=5,
∴OC=4,
∴点A的坐标是(4,3),
故选:D.
【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.
9.D
【分析】设,则,利用长方形纸片中,现将其沿对折,使得点C与点A重合,由勾股定理求即可.
【详解】解:∵长方形纸片中,,,现将其沿对折,使得点C与点A重合,
∴,,,
设,则,
在中,∵,
∴,
解得:.
即的长为.
故选:D.
【点睛】本题考查了图形的翻折变换,勾股定理的应用,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变是解题关键.
10.D
【分析】分为两种情况:斜边是有一条直角边是,和都是直角边,根据勾股定理求出即可.
【详解】解:如图,
分为两种情况:斜边是有一条直角边是,
由勾股定理得:第三边长是;
和都是直角边,
由勾股定理得:第三边长是;
即第三边长是或,
故选:D.
【点睛】本题考查了对勾股定理的应用,注意:在直角三角形中的两条直角边、的平方和等于斜边的平方.
11.5或
【分析】已知直角三角形两边的长,但没有明确是直角边还是斜边,因此分两种情况讨论.
【详解】解:①长为3的边是直角边,长为4的边是斜边时,
第三边的长为:;
②长为3、4的边都是直角边时,
第三边的长为:;
∴第三边的长为:或5,
故答案为:或5.
12.(1)
(2)画图见解析;如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求
【分析】(1)在网格中用勾股定理求解即可;
(2)取与网格线的交点E,F,连接并延长与网格线相交于点M,连接;连接与网格线相交于点G,连接并延长与网格线相交于点H,连接并延长与圆相交于点I,连接并延长与的延长线相交于点Q,则点Q即为所求,连接,,过点E作网格线,过点G作网格线,由图可得,根据全等三角形的性质可得和,根据同弧所对圆周角相等可得,进而得到和,再通过证明即可得到结论.
【详解】(1)解:;
故答案为:.
(2)解:如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求;
连接,,过点E作网格线,过点G作网格线,
由图可得:∵,,,
∴,
∴,,
∵,
∴,即,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∵是等边三角形,
∴,即,
∴,即,
∵,,,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,此时点Q即为所求;
故答案为:如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求.
【点睛】本题考查作图—复杂作图,勾股定理、等边三角形的判定、全等三角形的判定与性质等知识,解题关键是理解题意,灵活运用所学知识是关键.
13.25
【分析】把立体几何图展开得到平面几何图,如图,然后利用勾股定理计算AB,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】解:展开图为:
则AC=20dm,BC=3×3+2×3=15(dm),
在Rt△ABC中, (dm).
所以蚂蚁所走的最短路线长度为25 dm.
故答案为:25.
【点睛】本题考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.
14.
【分析】由折叠性质可知,然后根据三角不等关系可进行求解.
【详解】解:∵,
∴,
由折叠的性质可知,
∵,
∴当、、B三点在同一条直线时,取最小值,最小值即为;
故答案为.
【点睛】本题主要考查勾股定理、折叠的性质及三角不等关系,熟练掌握勾股定理、折叠的性质及三角不等关系是解题的关键.
15.5
【分析】根据勾股定理可知,以直角三角形斜边为边的正方形面积等于以直角三角形两直角边为边的正方形面积之和,依照此可求出正方形E的面积.
【详解】解:由勾股定理可知:,
∴,
由勾股定理可知:,
∴,
故答案为:5.
【点睛】本题考查勾股定理的实际应用,能够将勾股定理与几何之间的面积关系相结合是解决本题的关键.
16.
【分析】先把圆柱体沿剪开,则的长为圆柱体的底面圆周长的一半,在中,利用勾股定理即可求出的长.
【详解】解:圆柱体的侧面展开图如图所示,
∵底面圆周长为,
∴,
又∵,
∴在中,.
故答案为.
【点睛】本题考查了平面展开---最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
17.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据轴对称的性质找到关于直线的对称点,,连接,则线段即为所求;
(2)根据平移的性质得到线段即为所求;
(3)勾股定理求得,,则证明得出,则,则点即为所求.
【详解】(1)解:如图所示,线段即为所求;
(2)解:如图所示,线段即为所求;
(3)解:如图所示,点即为所求
如图所示,
∵,,
∴,
又,
∴,
∴,
又,
∴
∴,
∴垂直平分.
【点睛】本题考查了轴对称作图,平移作图,勾股定理与网格问题,熟练掌握以上知识是解题的关键.
18.(1)CD=
(2)
【分析】(1)根据勾股定理先求出AB,再根据“双求法”求出CD的长度;
(2)在Rt△ABD和Rt△ADC中,分别利用勾股定理表示出,然后得到关于x的方程,解方程即可.
【详解】(1)解:在Rt△ABC中,AB=,
由面积的两种算法可得:,
解得:CD=;
(2)在Rt△ABD中,,
在Rt△ADC中,,
所以,
解得:.
【点睛】此题主要考查的是勾股定理的应用,熟知直角三角形两直角边的平方和等于斜边的平方是解题的关键.
19.(1)见解析
(2)
【分析】(1)由求出,然后利用证明,可得,再由等边对等角得出结论;
(2)过点E作于F,根据等腰三角形的性质和含直角三角形的性质求出和,然后利用勾股定理求出,再根据三角形面积公式计算即可.
【详解】(1)证明:∵,
∴,即,
∴,
在和中,,
∴,
∴,
∴;
(2)解:过点E作于F,
由(1)知,
∵,
∴,
∵,
∴,
∴,,
∴.
【点睛】本题考查了三角形内角和定理,全等三角形的判定和性质,等腰三角形的性质,含直角三角形的性质以及勾股定理等知识,正确寻找证明三角形全等的条件是解题的关键.
20.(1),
(2)见解析
(3)见解析
【分析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【详解】(1)解:∵
∴,
∵
∴
即;
(2)证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
(3)证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,以点为圆心,长为半径作弧,交于点,再分别以,为圆心,以大于的长为半径作弧,两弧交于点,作射线交于点.若,,则的长为( )
A. B. C.4 D.
2.如图,长方体的长为3,宽为2,高为4,一只蚂蚁从点A出发,沿长方体表面到点B处吃食物,那么它爬行最短路程是( )
A.7 B. C. D.
3.如图,平行四边形的对角线,相交于点,且,点为边上一动点(不与点A,重合),于点,于点,若,,则的最小值为( )
A.3 B.2 C. D.
4.《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几 ”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长 ”如图,若设秋千绳索长为x尺,则可列方程为( )
A. B.
C. D.
5.如图,是直角三角形,,分别以、为边向两侧作正方形.若图中两个正方形的面积和,则 .
6.如图,点P,Q关于直线l对称,点A,B为直线l上不同的两个点(点A在点B的左侧),连接.已知,,点A不在内部,则线段的长不可能为( ).
A.2 B.4 C. D.
7.蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为,则点的坐标为( )
A. B. C. D.
8.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A. B. C. D.
9.如图所示,长方形纸片中,,,现将其沿对折,使得点与点重合,则长为( )
A. B. C. D.
10.已知一个直角三角形的两边长分别为和,则第三边长是( )
A. B. C. D.或
二、填空题
11.已知直角三角形的两边长分别为3、4.则第三边长为 .
12.如图,在每个小正方形的边长为1的网格中,等边三角形内接于圆,且顶点A,B均在格点上.
(1)线段的长为 ;
(2)若点D在圆上,与相交于点P.请用无刻度的直尺,在如图所示的网格中,画出点Q,使为等边三角形,并简要说明点Q的位置是如何找到的(不要求证明) .
13.如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3 dm、2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是 dm.
14.如图,在中,,点在边上.将沿折叠,使点落在点处,连接,则的最小值为 .
15.如图,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为7,18,30,则正方形B的面积为 .
16.如图,圆柱体的底面圆周长为,高为,是上底面的直径.一只蚂蚁从点出发,沿着圆柱的侧面爬行到点,则爬行的最短路程为 .
三、解答题
17.如图,在由边长为1个单位长度的小正方形组成的网格中,点均为格点(网格线的交点).
(1)画出线段关于直线对称的线段;
(2)将线段向左平移2个单位长度,再向上平移1个单位长度,得到线段,画出线段;
(3)描出线段上的点及直线上的点,使得直线垂直平分.
18.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于c2,另一种是等于四个直角三角形与一个小正方形的面积之和,即ab×4+(b-a)2,从而得到等式c2=ab×4+(b-a)2,化简便得结论a2+b2=c2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题:
如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
19.如图,在四边形中,点E是边上一点,且,.
求证:;
若,时,求的面积.
20.如图,.
写出与的数量关系
延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了作图-复杂作图、勾股定理,解决本题的关键是熟练掌握线段垂直平分线的性质.根据作图过程可得是的垂直平分线,根据勾股定理可得的长,再根据等面积法即可求出的长.
【详解】解:在中,,,,
,
由作图知,,
,
,
故选:D.
2.B
【分析】作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.本题考查的是平面展开最短路径问题,熟知此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.
【详解】解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是6和3,
则所走的最短线段是;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是5和4,
所以走的最短线段是;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是7和2,
所以走的最短线段是;
三种情况比较而言,第二种情况最短.
∵
∴它需要爬行的最短路线的长是,
故选:B.
3.C
【分析】本题考查了矩形的判定和性质,垂线段最短,勾股定理,先根据勾股定理计算出,再证明四边形是矩形,得到,再根据垂线段最短求出的最小值即可.
【详解】解:如下图所示,连接,
∵,且四边形是平行四边形,
∴,,
∴,
∵,,,
∴四边形是矩形,
∴,
∴当最小时,最小,
当时,当最小,
当时,,
∴,
故选:C.
4.C
【分析】此题主要考查了考差了勾股定理的应用,关键是正确理解题意,表示出 的长,掌握直角三角形中两直角边的平方和等于斜边的平方.设秋千的绳索长为 尺,根据题意可得尺,利用勾股定理可得方程.
【详解】解:设秋千的绳索长为 尺,根据题意可列方程为:即.
故选:C
5.6
【分析】本题考查了勾股定理,熟练掌握勾股定理是解题的关键.
根据勾股定理即可求解.
【详解】解:在中,由勾股定理得,,
∵,,,
∴,
故答案为:6.
6.A
【分析】本题考查轴对称的性质,勾股定理,实数大小比较.
先根据轴对称的性质,得,再求出当时 ,,然后由点A不在内部,得出,最后由,即可得出答案.
【详解】解:当时 ,
∵点P,Q关于直线l对称,点A,B为直线l上不同的两个点,
∴,,
∵
∴,
由勾股定理,得
∵点A不在内部,
∴
∵
∴的长不可能为2,
故选:A.
7.A
【分析】连接,设正六边形的边长为a,由正六边形的性质及点P的坐标可求得a的值,即可求得点M的坐标.
【详解】解:连接,如图,设正六边形的边长为a,
∵,
∴,
∵,
∴,
∴,
∴,,
∵点P的坐标为,
∴,
即;
∴,,
∴点M的坐标为.
故选:A.
【点睛】本题考查了坐标与图形,正六边形的性质,勾股定理,含30度角直角三角形的性质等知识,掌握这些知识是解题的关键.
8.D
【分析】利用HL证明△ACO≌△BCO,利用勾股定理得到OC=4,即可求解.
【详解】解:∵AB⊥x轴,
∴∠ACO=∠BCO=90°,
∵OA=OB,OC=OC,
∴△ACO≌△BCO(HL),
∴AC=BC=AB=3,
∵OA=5,
∴OC=4,
∴点A的坐标是(4,3),
故选:D.
【点睛】本题考查了坐标与图形,全等三角形的判定和性质,勾股定理,解题的关键是灵活运用所学知识解决问题.
9.D
【分析】设,则,利用长方形纸片中,现将其沿对折,使得点C与点A重合,由勾股定理求即可.
【详解】解:∵长方形纸片中,,,现将其沿对折,使得点C与点A重合,
∴,,,
设,则,
在中,∵,
∴,
解得:.
即的长为.
故选:D.
【点睛】本题考查了图形的翻折变换,勾股定理的应用,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变是解题关键.
10.D
【分析】分为两种情况:斜边是有一条直角边是,和都是直角边,根据勾股定理求出即可.
【详解】解:如图,
分为两种情况:斜边是有一条直角边是,
由勾股定理得:第三边长是;
和都是直角边,
由勾股定理得:第三边长是;
即第三边长是或,
故选:D.
【点睛】本题考查了对勾股定理的应用,注意:在直角三角形中的两条直角边、的平方和等于斜边的平方.
11.5或
【分析】已知直角三角形两边的长,但没有明确是直角边还是斜边,因此分两种情况讨论.
【详解】解:①长为3的边是直角边,长为4的边是斜边时,
第三边的长为:;
②长为3、4的边都是直角边时,
第三边的长为:;
∴第三边的长为:或5,
故答案为:或5.
12.(1)
(2)画图见解析;如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求
【分析】(1)在网格中用勾股定理求解即可;
(2)取与网格线的交点E,F,连接并延长与网格线相交于点M,连接;连接与网格线相交于点G,连接并延长与网格线相交于点H,连接并延长与圆相交于点I,连接并延长与的延长线相交于点Q,则点Q即为所求,连接,,过点E作网格线,过点G作网格线,由图可得,根据全等三角形的性质可得和,根据同弧所对圆周角相等可得,进而得到和,再通过证明即可得到结论.
【详解】(1)解:;
故答案为:.
(2)解:如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求;
连接,,过点E作网格线,过点G作网格线,
由图可得:∵,,,
∴,
∴,,
∵,
∴,即,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∵是等边三角形,
∴,即,
∴,即,
∵,,,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,此时点Q即为所求;
故答案为:如图,取与网格线的交点E,F,连接并延长与网格线相交于点G;连接与网格线相交于点H,连接并延长与网格线相交于点I,连接并延长与圆相交于点K,连接并延长与的延长线相交于点Q,则点Q即为所求.
【点睛】本题考查作图—复杂作图,勾股定理、等边三角形的判定、全等三角形的判定与性质等知识,解题关键是理解题意,灵活运用所学知识是关键.
13.25
【分析】把立体几何图展开得到平面几何图,如图,然后利用勾股定理计算AB,则根据两点之间线段最短得到蚂蚁所走的最短路线长度.
【详解】解:展开图为:
则AC=20dm,BC=3×3+2×3=15(dm),
在Rt△ABC中, (dm).
所以蚂蚁所走的最短路线长度为25 dm.
故答案为:25.
【点睛】本题考查了勾股定理的应用,把立体几何图中的问题转化为平面几何图中的问题是解题的关键.
14.
【分析】由折叠性质可知,然后根据三角不等关系可进行求解.
【详解】解:∵,
∴,
由折叠的性质可知,
∵,
∴当、、B三点在同一条直线时,取最小值,最小值即为;
故答案为.
【点睛】本题主要考查勾股定理、折叠的性质及三角不等关系,熟练掌握勾股定理、折叠的性质及三角不等关系是解题的关键.
15.5
【分析】根据勾股定理可知,以直角三角形斜边为边的正方形面积等于以直角三角形两直角边为边的正方形面积之和,依照此可求出正方形E的面积.
【详解】解:由勾股定理可知:,
∴,
由勾股定理可知:,
∴,
故答案为:5.
【点睛】本题考查勾股定理的实际应用,能够将勾股定理与几何之间的面积关系相结合是解决本题的关键.
16.
【分析】先把圆柱体沿剪开,则的长为圆柱体的底面圆周长的一半,在中,利用勾股定理即可求出的长.
【详解】解:圆柱体的侧面展开图如图所示,
∵底面圆周长为,
∴,
又∵,
∴在中,.
故答案为.
【点睛】本题考查了平面展开---最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
17.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据轴对称的性质找到关于直线的对称点,,连接,则线段即为所求;
(2)根据平移的性质得到线段即为所求;
(3)勾股定理求得,,则证明得出,则,则点即为所求.
【详解】(1)解:如图所示,线段即为所求;
(2)解:如图所示,线段即为所求;
(3)解:如图所示,点即为所求
如图所示,
∵,,
∴,
又,
∴,
∴,
又,
∴
∴,
∴垂直平分.
【点睛】本题考查了轴对称作图,平移作图,勾股定理与网格问题,熟练掌握以上知识是解题的关键.
18.(1)CD=
(2)
【分析】(1)根据勾股定理先求出AB,再根据“双求法”求出CD的长度;
(2)在Rt△ABD和Rt△ADC中,分别利用勾股定理表示出,然后得到关于x的方程,解方程即可.
【详解】(1)解:在Rt△ABC中,AB=,
由面积的两种算法可得:,
解得:CD=;
(2)在Rt△ABD中,,
在Rt△ADC中,,
所以,
解得:.
【点睛】此题主要考查的是勾股定理的应用,熟知直角三角形两直角边的平方和等于斜边的平方是解题的关键.
19.(1)见解析
(2)
【分析】(1)由求出,然后利用证明,可得,再由等边对等角得出结论;
(2)过点E作于F,根据等腰三角形的性质和含直角三角形的性质求出和,然后利用勾股定理求出,再根据三角形面积公式计算即可.
【详解】(1)证明:∵,
∴,即,
∴,
在和中,,
∴,
∴,
∴;
(2)解:过点E作于F,
由(1)知,
∵,
∴,
∵,
∴,
∴,,
∴.
【点睛】本题考查了三角形内角和定理,全等三角形的判定和性质,等腰三角形的性质,含直角三角形的性质以及勾股定理等知识,正确寻找证明三角形全等的条件是解题的关键.
20.(1),
(2)见解析
(3)见解析
【分析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【详解】(1)解:∵
∴,
∵
∴
即;
(2)证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
(3)证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
答案第1页,共2页
答案第1页,共2页
