2024届四川省泸州市中考数学试卷(含答案)
文档属性
| 名称 | 2024届四川省泸州市中考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-17 00:00:00 | ||
图片预览



文档简介
四川省泸州市2024届中考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各数中,无理数是( )
A. B. C.0 D.π
2.第二十届中国国际酒业博览会于2024年3月21-24日在泸州市国际会展中心举办,各种活动带动消费亿元,将数据用科学记数法表示为( )
A. B. C. D.
3.下列几何体中,其三视图的主视图和左视图都为矩形的是( )
A. B. C. D.
4.把一块含角的直角三角板按如图方式放置于两条平行线间,若,则( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知四边形是平行四边形,下列条件中,不能判定为矩形的是( )
A. B. C. D.
7.分式方程的解是( )
A. B. C. D.
8.已知关于x的一元二次方程无实数根,则函数与函数的图象交点个数为( )
A.0 B.1 C.2 D.3
9.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
10.宽与长的比是的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.如图,把黄金矩形沿对角线翻折,点B落在点处,交于点E,则的值为( )
A. B. C. D.
11.已知二次函数(x是自变量)的图象经过第一、二、四象限,则实数a的取值范围为( )
A. B. C. D.
12.如图,在边长为6的正方形中,点E,F分别是边,上的动点,且满足,与交于点O,点M是的中点,G是边上的点,,则的最小值是( )
A.4 B.5 C.8 D.10
二、填空题
13.函数中,自变量x的取值范围是________.
14.在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为________.
15.已知,是一元二次方程的两个实数根,则的值是________.
16.定义:在平面直角坐标系中,将一个图形先向上平移个单位,再绕原点按逆时针方向旋转角度,这样的图形运动叫做图形的变换.如:点按照变换后得到点的坐标为,则点按照变换后得到点的坐标为________.
三、解答题
17.计算:.
18.如图,在中,E,F是对角线上的点,且.求证:.
19.化简:.
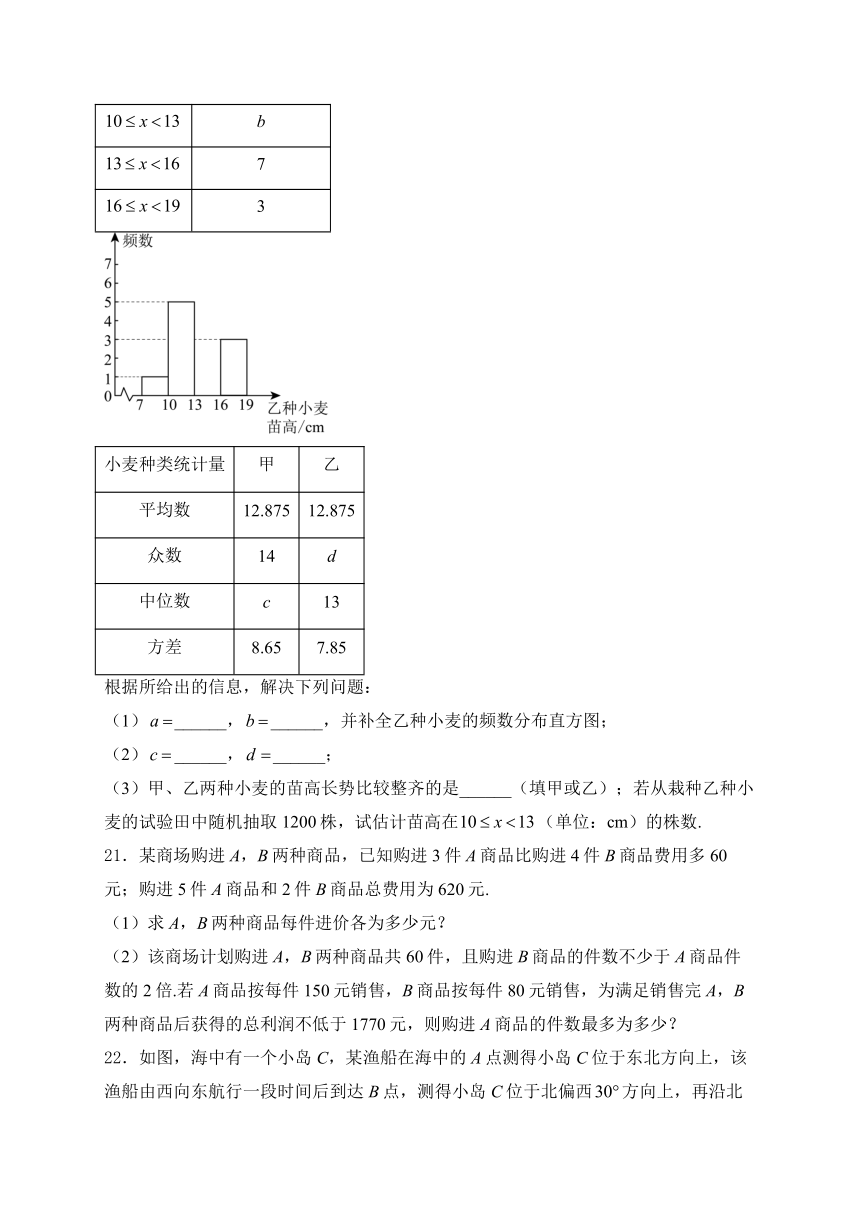
20.某地两块试验田中分别栽种了甲、乙两种小麦,为了考察这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如下表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
a
b
7
3
小麦种类统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)______,______,并补全乙种小麦的频数分布直方图;
(2)______,______;
(3)甲、乙两种小麦的苗高长势比较整齐的是______(填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在(单位:cm)的株数.
21.某商场购进A,B两种商品,已知购进3件A商品比购进4件B商品费用多60元;购进5件A商品和2件B商品总费用为620元.
(1)求A,B两种商品每件进价各为多少元?
(2)该商场计划购进A,B两种商品共60件,且购进B商品的件数不少于A商品件数的2倍.若A商品按每件150元销售,B商品按每件80元销售,为满足销售完A,B两种商品后获得的总利润不低于1770元,则购进A商品的件数最多为多少?
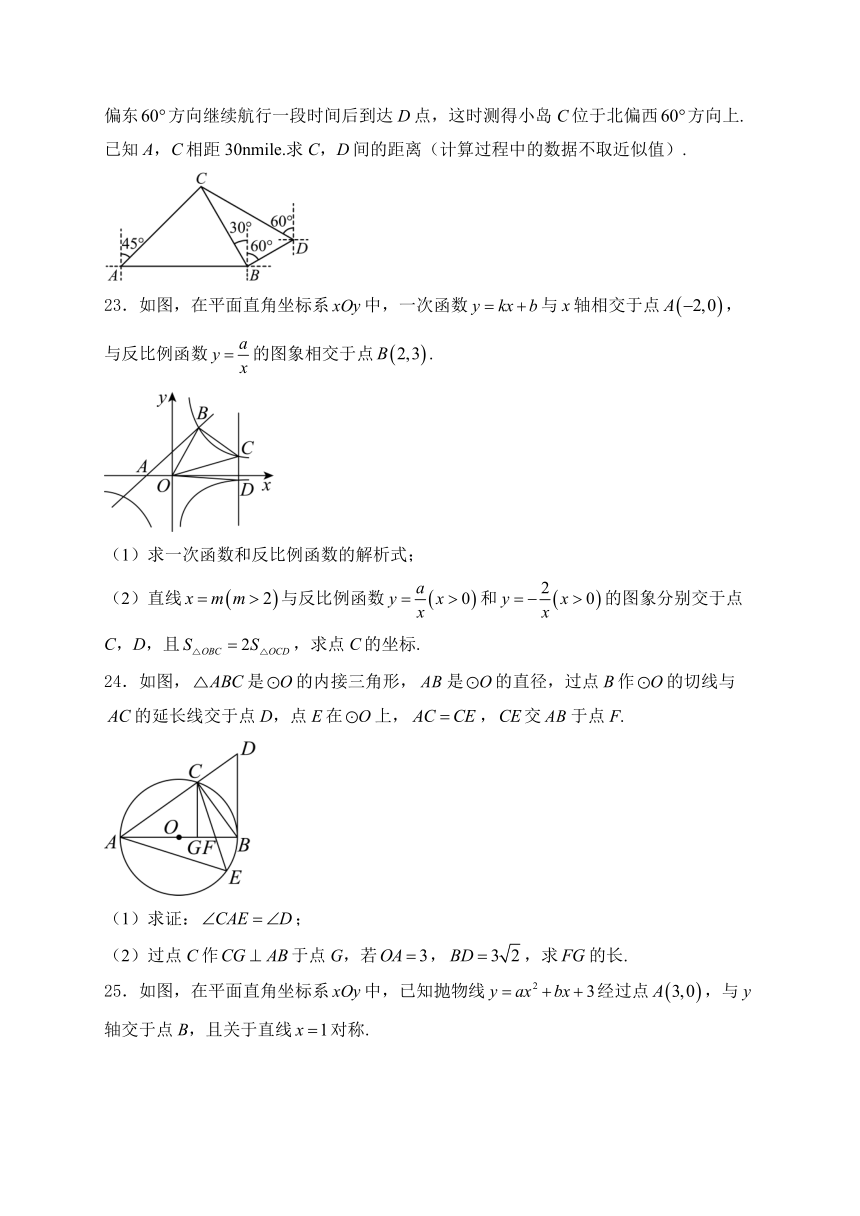
22.如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西方向上,再沿北偏东方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西方向上.已知A,C相距30nmile.求C,D间的距离(计算过程中的数据不取近似值).
23.如图,在平面直角坐标系中,一次函数与x轴相交于点,与反比例函数的图象相交于点.
(1)求一次函数和反比例函数的解析式;
(2)直线与反比例函数和的图象分别交于点C,D,且,求点C的坐标.
24.如图,是的内接三角形,是的直径,过点B作的切线与的延长线交于点D,点E在上,,交于点F.
(1)求证:;
(2)过点C作于点G,若,,求的长.
25.如图,在平面直角坐标系中,已知抛物线经过点,与y轴交于点B,且关于直线对称.
(1)求该抛物线的解析式;
(2)当时,y的取值范围是,求t的值;
(3)点C是抛物线上位于第一象限的一个动点,过点C作x轴的垂线交直线于点D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形?若存在,求出该菱形的边长;若不存在,说明理由.
参考答案
1.答案:D
解析:根据无理数的定义可知,四个数中,只有D选项中的数π是无理数,
故选:D.
2.答案:B
解析:,
故选:B.
3.答案:C
解析:A、主视图为三角形,左视图为三角形,故本选项不符合题意;
B、主视图为三角形,左视图为三角形,故本选项不符合题意;
C、主视图为矩形,左视图为矩形,故本选项符合题意;
D、主视图为矩形,左视图为三角形,故本选项不符合题意.
故选:C.
4.答案:B
解析:如图,
直角三角板位于两条平行线间且,
,
又直角三角板含角,
,
,
故选:B.
5.答案:C
解析:A、与不是同类项,不能合并,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、,原式计算错误,不符合题意;
故选:C.
6.答案:D
解析:如图,
A、,能判定为矩形,本选项不符合题意;
B、,,,能判定为矩形,本选项不符合题意;
C、,能判定为矩形,本选项不符合题意;
D、,能判定为菱形,不能判定为矩形,本选项符合题意;
故选:D.
7.答案:D
解析:,
,
,
,
,
,
经检验是该方程的解,
故选:D.
8.答案:A
解析:方程无实数根,
,
解得:,则函数的图象过二,四象限,
而函数的图象过一,三象限,
函数与函数的图象不会相交,则交点个数为0,
故选:A.
9.答案:C
解析:如图,连接,
四边形是的内接四边形,
,
,
,
即,
,
,是的切线,根据切线长定理得,
,
,
.
故选:C.
10.答案:A
解析:设宽为x,
宽与长的比是,
长为:,
由折叠的性质可知,,
在和中,
,
,
,
,
设,
在中,,
变形得:,
,,
,
故选A.
11.答案:A
解析:二次函数图象经过第一、二、四象限,
且,,
解得.
故选:A.
12.答案:B
解析:四边形是正方形,
,,
又,
,
,
,
点M是的中点,
;
如图所示,在延长线上截取,连接,
,,,
,
,
,
当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,
,,
,
,
在中,由勾股定理得,
的最小值为5,
故选:B.
13.答案:
解析:在实数范围内有意义,
,
,
故答案为.
14.答案:3
解析:设黄球的个数为x个,
根据题意得:,
解得:,
经检验,是原分式方程的解,
黄球的个数为3个.
故答案为:3.
15.答案:14
解析:,是一元二次方程的两个实数根,
,,
,
,
.
故答案为:14.
16.答案:
解析:根据题意,点向上平移2个单位,得到点,
,,
,,
,
根据题意,将点绕原点按逆时针方向旋转,
,
作轴于点D,
,,
,
点的坐标为,
故答案为:.
17.答案:3
解析:原式,
,
.
18.答案:证明见解析
解析:证明:四边形是平行四边形,
,,
,
又,
,
.
19.答案:
解析:
.
20.答案:(1)2,4,乙种小麦的频数分布直方图见解析
(2)13,13.5
(3)乙,375
解析:(1)由表可知:甲种小麦苗高在的有7、8,故;
甲种小麦苗高在的有10、11、11、12,故,
(株),
补全后的乙种小麦的频数分布直方图如下:
故答案为:2,4;
(2)由表可知:乙种小麦苗高最多,为5次,故;
将甲种小麦苗高从小到大排列得7、8、10、11、11、12、13、13、14、14、14、14、15、16、16、18,故中位数为,即;
故答案为:13.5,13;
(3)乙种小麦方差甲种小麦方差8.65,
甲、乙两种小麦的苗高长势比较整齐的是乙,
由题可知:乙种小麦随机抽取16株麦苗中苗高在有5株,
若从栽种乙种小麦的试验田中随机抽取1200株,苗高在的株数为:
(株).
21.答案:(1)A,B两种商品每件进价各为100元,60元
(2)购进A商品的件数最多为20件
解析:(1)设A,B两种商品每件进价各为x元,y元,
由题意得,,
解得,
答:A,B两种商品每件进价各为100元,60元;
(2)设购进A商品的件数为m件,则购进B商品的件数为件,
由题意得,,
解得,
为整数,
的最大值为20,
答:购进A商品的件数最多为20件.
22.答案:C,D间的距离为
解析:作于点E,
由题意得,,,
是等腰直角三角形,
,
,
在中,,
在中,,,
在中,,
答:C,D间的距离为.
23.答案:(1)一次函数解析式为,反比例函数解析式为
(2)
解析:(1)把代入中得:,解得,
反比例函数解析式为;
把,代入中得:,
,
一次函数解析式为;
(2)如图所示,过点B作轴于E,设与x轴交于F,
直线与反比例函数和的图象分别交于点C,D,
,,
,
;
轴,点B在反比例函数的图象上,
,
,
,
设,则,,
,
,,
,
,
解得或(舍去),
经检验是原方程的解,且符合题意,
.
24.答案:(1)证明见解析
(2)
解析:(1)证明:是的直径,
,
,
;
是的切线,
,
,
,
,
,
,
,
;
(2),
,
在中,由勾股定理得,
,
,
,
同理可得,
,
;
如图所示,过点C作于H,则,
由(1)可得,,
,
,即,
,
;
设,则,
,,
,
,即,
,
在中,由勾股定理得,
,
解得或(舍去),
.
25.答案:(1)
(2)
(3)存在点以B,C,D,E为顶点的四边形是菱形,边长为或2
解析:(1)抛物线经过点,与y轴交于点B,且关于直线对称,
,解得:,
;
(2)抛物线的开口向下,对称轴为直线,
抛物线上点到对称轴上的距离越远,函数值越小,
时,,
①当时,则:当时,函数有最大值,即:,
解得:或,均不符合题意,舍去;
②当时,则:当时,函数有最大值,即:,
解得:;
故;
(3)存在;
当时,解得:,,当时,,
,,
设直线的解析式为,把代入,得:,
,
设,则:,
,,,
当B,C,D,E为顶点的四边形是菱形时,分两种情况:
①当为边时,则:,即,
解得:(舍去)或,
此时菱形的边长为;
②当为对角线时,则:,即:,
解得:或(舍去)
此时菱形的边长为:;
综上:存在以B,C,D,E为顶点的四边形是菱形,边长为或2.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各数中,无理数是( )
A. B. C.0 D.π
2.第二十届中国国际酒业博览会于2024年3月21-24日在泸州市国际会展中心举办,各种活动带动消费亿元,将数据用科学记数法表示为( )
A. B. C. D.
3.下列几何体中,其三视图的主视图和左视图都为矩形的是( )
A. B. C. D.
4.把一块含角的直角三角板按如图方式放置于两条平行线间,若,则( )
A. B. C. D.
5.下列运算正确的是( )
A. B. C. D.
6.已知四边形是平行四边形,下列条件中,不能判定为矩形的是( )
A. B. C. D.
7.分式方程的解是( )
A. B. C. D.
8.已知关于x的一元二次方程无实数根,则函数与函数的图象交点个数为( )
A.0 B.1 C.2 D.3
9.如图,,是的切线,切点为A,D,点B,C在上,若,则( )
A. B. C. D.
10.宽与长的比是的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.如图,把黄金矩形沿对角线翻折,点B落在点处,交于点E,则的值为( )
A. B. C. D.
11.已知二次函数(x是自变量)的图象经过第一、二、四象限,则实数a的取值范围为( )
A. B. C. D.
12.如图,在边长为6的正方形中,点E,F分别是边,上的动点,且满足,与交于点O,点M是的中点,G是边上的点,,则的最小值是( )
A.4 B.5 C.8 D.10
二、填空题
13.函数中,自变量x的取值范围是________.
14.在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为________.
15.已知,是一元二次方程的两个实数根,则的值是________.
16.定义:在平面直角坐标系中,将一个图形先向上平移个单位,再绕原点按逆时针方向旋转角度,这样的图形运动叫做图形的变换.如:点按照变换后得到点的坐标为,则点按照变换后得到点的坐标为________.
三、解答题
17.计算:.
18.如图,在中,E,F是对角线上的点,且.求证:.
19.化简:.
20.某地两块试验田中分别栽种了甲、乙两种小麦,为了考察这两种小麦的长势,分别从中随机抽取16株麦苗,测得苗高(单位:cm)如下表.
甲 7 8 10 11 11 12 13 13 14 14 14 14 15 16 16 18
乙 7 10 13 11 18 12 13 13 10 13 13 14 15 16 11 17
将数据整理分析,并绘制成以下不完整的统计表格和频数分布直方图.
苗高分组 甲种小麦的频数
a
b
7
3
小麦种类统计量 甲 乙
平均数 12.875 12.875
众数 14 d
中位数 c 13
方差 8.65 7.85
根据所给出的信息,解决下列问题:
(1)______,______,并补全乙种小麦的频数分布直方图;
(2)______,______;
(3)甲、乙两种小麦的苗高长势比较整齐的是______(填甲或乙);若从栽种乙种小麦的试验田中随机抽取1200株,试估计苗高在(单位:cm)的株数.
21.某商场购进A,B两种商品,已知购进3件A商品比购进4件B商品费用多60元;购进5件A商品和2件B商品总费用为620元.
(1)求A,B两种商品每件进价各为多少元?
(2)该商场计划购进A,B两种商品共60件,且购进B商品的件数不少于A商品件数的2倍.若A商品按每件150元销售,B商品按每件80元销售,为满足销售完A,B两种商品后获得的总利润不低于1770元,则购进A商品的件数最多为多少?
22.如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西方向上,再沿北偏东方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西方向上.已知A,C相距30nmile.求C,D间的距离(计算过程中的数据不取近似值).
23.如图,在平面直角坐标系中,一次函数与x轴相交于点,与反比例函数的图象相交于点.
(1)求一次函数和反比例函数的解析式;
(2)直线与反比例函数和的图象分别交于点C,D,且,求点C的坐标.
24.如图,是的内接三角形,是的直径,过点B作的切线与的延长线交于点D,点E在上,,交于点F.
(1)求证:;
(2)过点C作于点G,若,,求的长.
25.如图,在平面直角坐标系中,已知抛物线经过点,与y轴交于点B,且关于直线对称.
(1)求该抛物线的解析式;
(2)当时,y的取值范围是,求t的值;
(3)点C是抛物线上位于第一象限的一个动点,过点C作x轴的垂线交直线于点D,在y轴上是否存在点E,使得以B,C,D,E为顶点的四边形是菱形?若存在,求出该菱形的边长;若不存在,说明理由.
参考答案
1.答案:D
解析:根据无理数的定义可知,四个数中,只有D选项中的数π是无理数,
故选:D.
2.答案:B
解析:,
故选:B.
3.答案:C
解析:A、主视图为三角形,左视图为三角形,故本选项不符合题意;
B、主视图为三角形,左视图为三角形,故本选项不符合题意;
C、主视图为矩形,左视图为矩形,故本选项符合题意;
D、主视图为矩形,左视图为三角形,故本选项不符合题意.
故选:C.
4.答案:B
解析:如图,
直角三角板位于两条平行线间且,
,
又直角三角板含角,
,
,
故选:B.
5.答案:C
解析:A、与不是同类项,不能合并,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、,原式计算错误,不符合题意;
故选:C.
6.答案:D
解析:如图,
A、,能判定为矩形,本选项不符合题意;
B、,,,能判定为矩形,本选项不符合题意;
C、,能判定为矩形,本选项不符合题意;
D、,能判定为菱形,不能判定为矩形,本选项符合题意;
故选:D.
7.答案:D
解析:,
,
,
,
,
,
经检验是该方程的解,
故选:D.
8.答案:A
解析:方程无实数根,
,
解得:,则函数的图象过二,四象限,
而函数的图象过一,三象限,
函数与函数的图象不会相交,则交点个数为0,
故选:A.
9.答案:C
解析:如图,连接,
四边形是的内接四边形,
,
,
,
即,
,
,是的切线,根据切线长定理得,
,
,
.
故选:C.
10.答案:A
解析:设宽为x,
宽与长的比是,
长为:,
由折叠的性质可知,,
在和中,
,
,
,
,
设,
在中,,
变形得:,
,,
,
故选A.
11.答案:A
解析:二次函数图象经过第一、二、四象限,
且,,
解得.
故选:A.
12.答案:B
解析:四边形是正方形,
,,
又,
,
,
,
点M是的中点,
;
如图所示,在延长线上截取,连接,
,,,
,
,
,
当H、D、F三点共线时,有最小值,即此时有最小值,最小值即为的长的一半,
,,
,
,
在中,由勾股定理得,
的最小值为5,
故选:B.
13.答案:
解析:在实数范围内有意义,
,
,
故答案为.
14.答案:3
解析:设黄球的个数为x个,
根据题意得:,
解得:,
经检验,是原分式方程的解,
黄球的个数为3个.
故答案为:3.
15.答案:14
解析:,是一元二次方程的两个实数根,
,,
,
,
.
故答案为:14.
16.答案:
解析:根据题意,点向上平移2个单位,得到点,
,,
,,
,
根据题意,将点绕原点按逆时针方向旋转,
,
作轴于点D,
,,
,
点的坐标为,
故答案为:.
17.答案:3
解析:原式,
,
.
18.答案:证明见解析
解析:证明:四边形是平行四边形,
,,
,
又,
,
.
19.答案:
解析:
.
20.答案:(1)2,4,乙种小麦的频数分布直方图见解析
(2)13,13.5
(3)乙,375
解析:(1)由表可知:甲种小麦苗高在的有7、8,故;
甲种小麦苗高在的有10、11、11、12,故,
(株),
补全后的乙种小麦的频数分布直方图如下:
故答案为:2,4;
(2)由表可知:乙种小麦苗高最多,为5次,故;
将甲种小麦苗高从小到大排列得7、8、10、11、11、12、13、13、14、14、14、14、15、16、16、18,故中位数为,即;
故答案为:13.5,13;
(3)乙种小麦方差甲种小麦方差8.65,
甲、乙两种小麦的苗高长势比较整齐的是乙,
由题可知:乙种小麦随机抽取16株麦苗中苗高在有5株,
若从栽种乙种小麦的试验田中随机抽取1200株,苗高在的株数为:
(株).
21.答案:(1)A,B两种商品每件进价各为100元,60元
(2)购进A商品的件数最多为20件
解析:(1)设A,B两种商品每件进价各为x元,y元,
由题意得,,
解得,
答:A,B两种商品每件进价各为100元,60元;
(2)设购进A商品的件数为m件,则购进B商品的件数为件,
由题意得,,
解得,
为整数,
的最大值为20,
答:购进A商品的件数最多为20件.
22.答案:C,D间的距离为
解析:作于点E,
由题意得,,,
是等腰直角三角形,
,
,
在中,,
在中,,,
在中,,
答:C,D间的距离为.
23.答案:(1)一次函数解析式为,反比例函数解析式为
(2)
解析:(1)把代入中得:,解得,
反比例函数解析式为;
把,代入中得:,
,
一次函数解析式为;
(2)如图所示,过点B作轴于E,设与x轴交于F,
直线与反比例函数和的图象分别交于点C,D,
,,
,
;
轴,点B在反比例函数的图象上,
,
,
,
设,则,,
,
,,
,
,
解得或(舍去),
经检验是原方程的解,且符合题意,
.
24.答案:(1)证明见解析
(2)
解析:(1)证明:是的直径,
,
,
;
是的切线,
,
,
,
,
,
,
,
;
(2),
,
在中,由勾股定理得,
,
,
,
同理可得,
,
;
如图所示,过点C作于H,则,
由(1)可得,,
,
,即,
,
;
设,则,
,,
,
,即,
,
在中,由勾股定理得,
,
解得或(舍去),
.
25.答案:(1)
(2)
(3)存在点以B,C,D,E为顶点的四边形是菱形,边长为或2
解析:(1)抛物线经过点,与y轴交于点B,且关于直线对称,
,解得:,
;
(2)抛物线的开口向下,对称轴为直线,
抛物线上点到对称轴上的距离越远,函数值越小,
时,,
①当时,则:当时,函数有最大值,即:,
解得:或,均不符合题意,舍去;
②当时,则:当时,函数有最大值,即:,
解得:;
故;
(3)存在;
当时,解得:,,当时,,
,,
设直线的解析式为,把代入,得:,
,
设,则:,
,,,
当B,C,D,E为顶点的四边形是菱形时,分两种情况:
①当为边时,则:,即,
解得:(舍去)或,
此时菱形的边长为;
②当为对角线时,则:,即:,
解得:或(舍去)
此时菱形的边长为:;
综上:存在以B,C,D,E为顶点的四边形是菱形,边长为或2.
同课章节目录
