2024届四川省遂宁市中考数学试卷(含答案)
文档属性
| 名称 | 2024届四川省遂宁市中考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-17 00:00:00 | ||
图片预览



文档简介
四川省遂宁市2024届中考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各数中,无理数是( )
A. B. C. D.0
2.古代中国诸多技艺均领先世界.榫卯结构就是其中之一,榫卯是在两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫(或榫头),凹进部分叫卯(或榫眼、榫槽),榫和卯咬合,起到连接作用,右图是某个部件“榫”的实物图,它的主视图是( )
A. B. C. D.
3.中国某汽车公司坚持“技术为王,创新为本”的发展理念,凭借研发实力和创新的发展模式在电池、电子、乘用车、商用车和轨道交通等多个领域发挥着举足轻重的作用.2024年第一季度,该公司以62万辆的销售成绩稳居新能源汽车销量榜榜首,市场占有率高达.将销售数据用科学计数法表示为( )
A. B. C. D.
4.下列运算结果正确的是( )
A. B.
C. D.
5.不等式组的解集在数轴上表示为( )
A. B.
C. D.
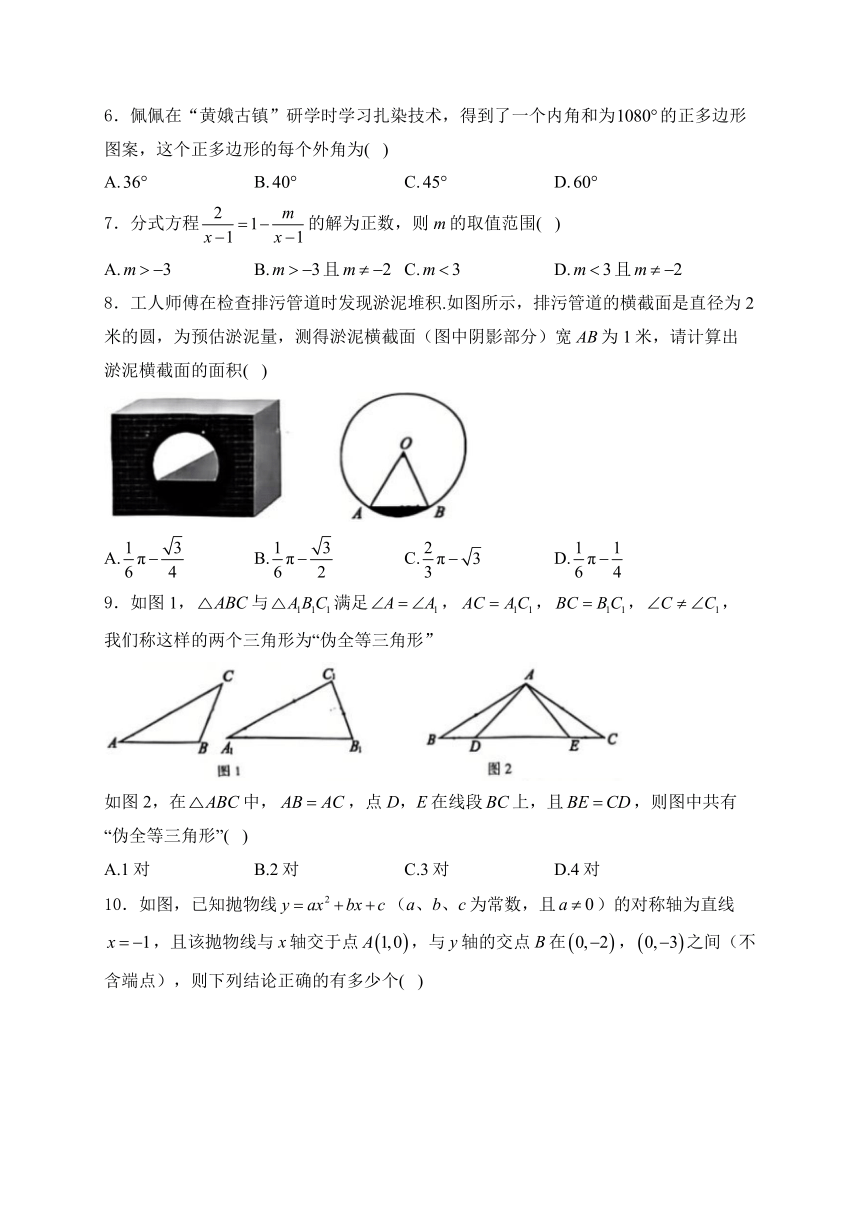
6.佩佩在“黄娥古镇”研学时学习扎染技术,得到了一个内角和为的正多边形图案,这个正多边形的每个外角为( )
A. B. C. D.
7.分式方程的解为正数,则m的取值范围( )
A. B.且 C. D.且
8.工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为2米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽AB为1米,请计算出淤泥横截面的面积( )
A. B. C. D.
9.如图1,与满足,,,,我们称这样的两个三角形为“伪全等三角形”
如图2,在中,,点D,E在线段上,且,则图中共有“伪全等三角形”( )
A.1对 B.2对 C.3对 D.4对
10.如图,已知抛物线(a、b、c为常数,且)的对称轴为直线,且该抛物线与x轴交于点,与y轴的交点B在,之间(不含端点),则下列结论正确的有多少个( )
①
②
③
④若方程两根为m,,则
A.1 B.2 C.3 D.4
二、填空题
11.分解因式:______.
12.反比例函数的图象在第一、三象限,则点在第______象限.
13.体育老师要在甲和乙两人中选择1人参加篮球投篮大赛,下表是两人5次训练成绩,从稳定的角度考虑,老师应该选______参加比赛.
甲 8 8 7 9 8
乙 6 9 7 9 9
14.在等边三边上分别取点D、E、F,使得,连接三点得到,易得,设,则
如图①当时,
如图②当时,
如图③当时,
……
直接写出,当时,______.
15.如图,在正方形纸片中,E是边的中点,将正方形纸片沿折叠,点B落在点P处,延长交于点Q,连结并延长交于点F.给出以下结论:
①为等腰三角形
②F为的中点
③
④.
其中正确结论是______.(填序号)
三、解答题
16.计算:.
17.先化简:,再从1,2,3中选择一个合适的数作为x的值代入求值.
18.康康在学习了矩形定义及判定定理1后,继续探究其它判定定理.
(1)实践与操作
①任意作两条相交的直线,交点记为O;
②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段;OA,OB,OC,OD
③顺次连结所得的四点得到四边形.
于是可以直接判定四边形是平行四边形,则该判定定理是:______.
(2)猜想与证明
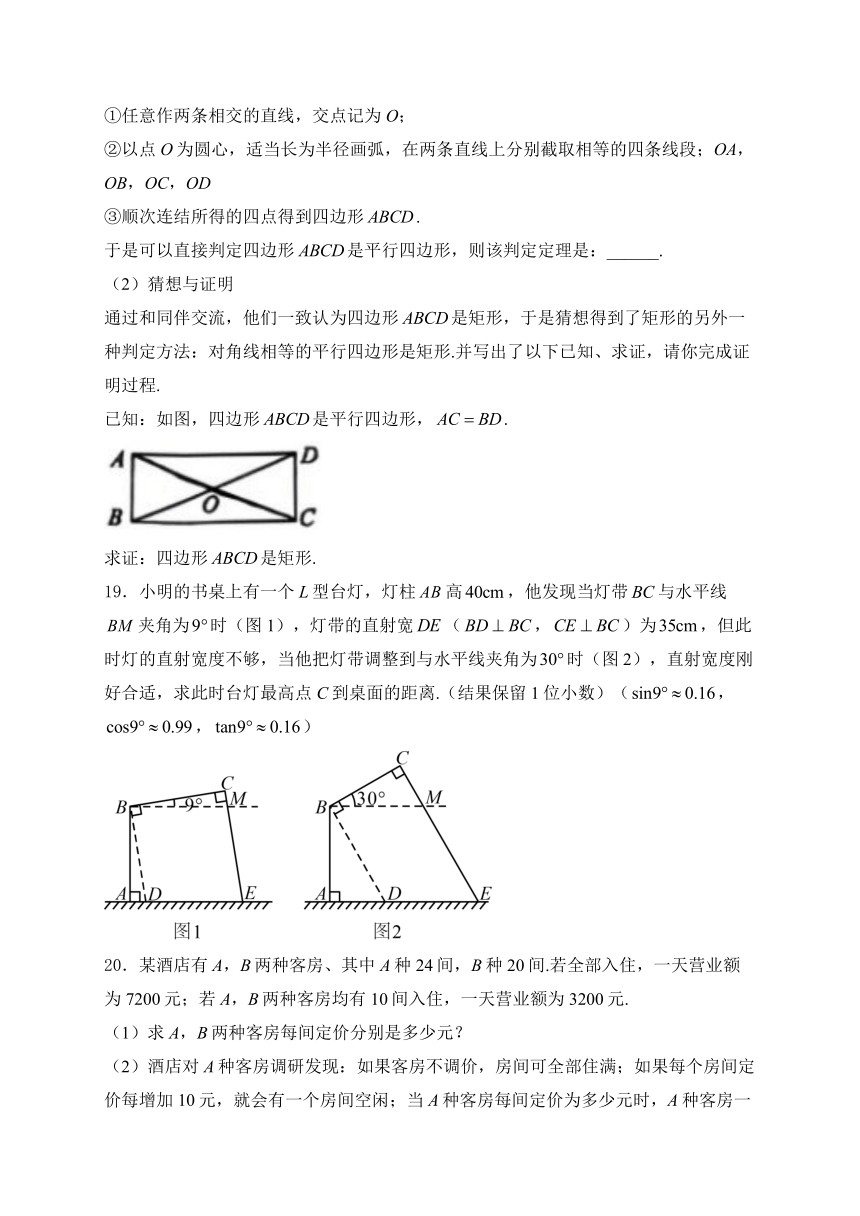
通过和同伴交流,他们一致认为四边形是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.
已知:如图,四边形是平行四边形,.
求证:四边形是矩形.
19.小明的书桌上有一个L型台灯,灯柱高,他发现当灯带与水平线夹角为时(图1),灯带的直射宽(,)为,但此时灯的直射宽度不够,当他把灯带调整到与水平线夹角为时(图2),直射宽度刚好合适,求此时台灯最高点C到桌面的距离.(结果保留1位小数)(,,)
20.某酒店有A,B两种客房、其中A种24间,B种20间.若全部入住,一天营业额为7200元;若A,B两种客房均有10间入住,一天营业额为3200元.
(1)求A,B两种客房每间定价分别是多少元?
(2)酒店对A种客房调研发现:如果客房不调价,房间可全部住满;如果每个房间定价每增加10元,就会有一个房间空闲;当A种客房每间定价为多少元时,A种客房一天的营业额W最大,最大营业额为多少元?
21.已知关于x的一元二次方程.
(1)求证:无论m取何值,方程都有两个不相等的实数根;
(2)如果方程的两个实数根为,,且,求m的值.
22.遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分内容,请完善报告:
xx小组关于xx学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 xx学校学生
数据的整理与描述
景点 A:中国死海 B:龙凤古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为______,扇形统计图中,______,“B:龙凤古镇”对应圆心角的度数是______; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
23.如图,一次函数的图象与反比例函数的图象相交于,两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求的面积.
24.如图,是的直径,是一条弦,点D是的中点,于点E,交于点F,连结交于点G.
(1)求证:;
(2)延长至点M,使,连结.
①求证:是的切线;
②若,,求的半径.
25.二次函数的图象与x轴分别交于点,,与y轴交于点,P,Q为抛物线上的两点.
(1)求二次函数的表达式;
(2)当P,C两点关于抛物线对轴对称,是以点P为直角顶点的直角三角形时,求点Q的坐标;
(3)设P的横坐标为m,Q的横坐标为,试探究:的面积S是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
参考答案
1.答案:C
解析:,,0都是有理数,是无理数,故选:C.
2.答案:A
解析:由实物图可知,从正面看到的图形是,故选:A.
3.答案:C
解析:万,故选:C.
4.答案:D
解析:A、,该选项错误,不合题意;
B、,该选项错误,不合题意;
C、,该选项错误,不合题意;
D、,该选项正确,符合题意;
故选:D.
5.答案:B
解析:,由①得,,由②得,,不等式组的解集为,不等式组的解集在数轴上表示为,故选:B.
6.答案:C
解析:设这个正多边形的边数为n,则,,这个正多边形的每个外角为,故选:C.
7.答案:B
解析:方程两边同时乘以得,,解得,分式方程的解为正数,,,又,即,,m的取值范围为且,故选:B.
8.答案:A
解析:过点O作于D,则,,
圆的直径为2米,,在中,,,为等边三角形,,淤泥横截面的面积,故选:A.
9.答案:D
解析:,,在和中,,,,在,中,,,,在,中,,,,在,中,,,,综上所述,共有4对“伪全等三角形”,故选:D.
10.答案:B
解析:由图可知,
抛物线的对称轴为直线,且该抛物线与x轴交于点,
,,
则,
抛物线与y轴的交点B在,之间,
,
则,故①错误;
设抛物线与x轴另一个交点,
对称轴为直线,且该抛物线与x轴交于点,
,解得,
则,故②错误;
,,,
,解得,故③正确;
根据抛物线与x轴交于点和,直线过点和,如图,
方程两根为m,n满足,故④正确;
故选:B.
11.答案:
解析:.故答案为:.
12.答案:四
解析:反比例函数的图象在第一、三象限,,,点在第四象限,故答案为:四.
13.答案:甲
解析:甲的平均数为,,乙的平均数为,,,甲成绩更稳定,应选甲参加比赛,
故答案为:甲.
14.答案:
解析:根据题意可得,当时,,则当时,,故答案为:.
15.答案:①②③
解析:如图所示,
E为的中点,,设正方形的边长为,则,折叠,,,,,是等腰三角形,故①正确;
设,,,,,又,四边形是平行四边形,,,即F是的中点,故②正确;
,,,在中,,,,设,则,,,,,,故③正确;
连接,如图所示,
,,,又,,,又,,,又,,,,,,在中,,,故④不正确,故答案为:①②③.
16.答案:2024
解析:
.
17.答案:2
解析:
,
,2,
当时,原式.
18.答案:(1)对角线互相平分的四边形是平行四边形
(2)证明见解析
解析:(1)由作图可得:,,
四边形是平行四边形,
(2)四边形是平行四边形,
,,
,
,,
,
,
四边形是矩形.
19.答案:此时台灯最高点C到桌面的距离为
解析:由已知,,
在图1中,,
,
,
四边形是平行四边形,
,
在中,,
在图2中,过点C作于点N,
,
灯柱高,
点C到桌面的距离为.
答:此时台灯最高点C到桌面的距离为.
20.答案:(1)A种客房每间定价为元,B种客房每间定价为元
(2)当A种客房每间定价为元时,A种客房一天的营业额W最大,最大营业额为元
解析:(1)设A种客房每间定价为x元,B种客房每间定价为y元,
由题意可得,,
解得,
答:A种客房每间定价为元,B种客房每间定价为元;
(2)设A种客房每间定价为a元,
则,
,
当时,W取最大值,元,
答:当A种客房每间定价为元时,A种客房一天的营业额W最大,最大营业额为元.
21.答案:(1)证明见解析
(2)或
解析:(1)证明:,
无论m取何值,,恒成立,
无论m取何值,方程都有两个不相等的实数根.
(2),是方程的两个实数根,
,,
,
解得:或.
22.答案:(1),10,
(2)见解析
(3)
(4)
解析:(1)本次被抽样调查的学生总人数为,
C组的人数为:,
,
,
B:龙凤古镇”对应圆心角的度数是.
故答案为:,10,.
(2)根据(1)可得C组人数为10人,补全统计图,如图所示,
(3).
答:请你估计该学校学生“五一”假期未出游的人数为人;
(4)列表如下,
A B C D
A
B
C
D
共有16种等可能结果,其中他们选择同一景点的情形有4种,
他们选择同一景点的概率为.
23.答案:(1)反比例函数表达式为,一次函数表达式为
(2)或
(3)8
解析:(1)把代入得,,,反比例函数表达式为,把代入得,,,,把、代入得,,解得,一次函数表达式为;
(2)由图象可得,当时,x的取值范围为或;
(3)如图,设直线与y轴相交于点D,过点A作轴于点M,过点C作轴于点N,则,,
点B、C关于原点对称,,,,,,即的面积为8.
24.答案:(1)证明见解析
(2)①证明见解析,②的半径为
解析:(1)证明:如图,连接,
点D是的中点,,,,为的直径,,,,.
(2)证明:①为的直径,,,,是的垂直平分线,,,,而,,,
,为的直径,是的切线;
②,,,,,,,,,,,,的半径为.
25.答案:(1)
(2)
(3)存在,最小值为
解析:(1)把,,代入得,,解得,二次函数的表达式为;
(2)如图:
由得抛物线对称轴为直线,P,C两点关于抛物线对轴对称,,,设,,,,整理得,,解得,(舍去),,;
(3)存在,理由:当点P、Q在x轴下方,且点Q在点P上方时,设点,则点,设直线交x轴于点H,
设直线表达式为:,代入,,得:,解得:,直线的表达式为:,令,得,则,则,则,即S存在最小值为;当点P、Q在x轴下方,且点P在点Q上方时,
同上可求直线表达式为:,令,得,则,则,则即S存在最小值为;当点P、Q都在x轴上方或者一个在x轴上方,一个在x轴下方同理可求,即S存在最小值为,综上所述,的面积S是否存在最小值,且为.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各数中,无理数是( )
A. B. C. D.0
2.古代中国诸多技艺均领先世界.榫卯结构就是其中之一,榫卯是在两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫(或榫头),凹进部分叫卯(或榫眼、榫槽),榫和卯咬合,起到连接作用,右图是某个部件“榫”的实物图,它的主视图是( )
A. B. C. D.
3.中国某汽车公司坚持“技术为王,创新为本”的发展理念,凭借研发实力和创新的发展模式在电池、电子、乘用车、商用车和轨道交通等多个领域发挥着举足轻重的作用.2024年第一季度,该公司以62万辆的销售成绩稳居新能源汽车销量榜榜首,市场占有率高达.将销售数据用科学计数法表示为( )
A. B. C. D.
4.下列运算结果正确的是( )
A. B.
C. D.
5.不等式组的解集在数轴上表示为( )
A. B.
C. D.
6.佩佩在“黄娥古镇”研学时学习扎染技术,得到了一个内角和为的正多边形图案,这个正多边形的每个外角为( )
A. B. C. D.
7.分式方程的解为正数,则m的取值范围( )
A. B.且 C. D.且
8.工人师傅在检查排污管道时发现淤泥堆积.如图所示,排污管道的横截面是直径为2米的圆,为预估淤泥量,测得淤泥横截面(图中阴影部分)宽AB为1米,请计算出淤泥横截面的面积( )
A. B. C. D.
9.如图1,与满足,,,,我们称这样的两个三角形为“伪全等三角形”
如图2,在中,,点D,E在线段上,且,则图中共有“伪全等三角形”( )
A.1对 B.2对 C.3对 D.4对
10.如图,已知抛物线(a、b、c为常数,且)的对称轴为直线,且该抛物线与x轴交于点,与y轴的交点B在,之间(不含端点),则下列结论正确的有多少个( )
①
②
③
④若方程两根为m,,则
A.1 B.2 C.3 D.4
二、填空题
11.分解因式:______.
12.反比例函数的图象在第一、三象限,则点在第______象限.
13.体育老师要在甲和乙两人中选择1人参加篮球投篮大赛,下表是两人5次训练成绩,从稳定的角度考虑,老师应该选______参加比赛.
甲 8 8 7 9 8
乙 6 9 7 9 9
14.在等边三边上分别取点D、E、F,使得,连接三点得到,易得,设,则
如图①当时,
如图②当时,
如图③当时,
……
直接写出,当时,______.
15.如图,在正方形纸片中,E是边的中点,将正方形纸片沿折叠,点B落在点P处,延长交于点Q,连结并延长交于点F.给出以下结论:
①为等腰三角形
②F为的中点
③
④.
其中正确结论是______.(填序号)
三、解答题
16.计算:.
17.先化简:,再从1,2,3中选择一个合适的数作为x的值代入求值.
18.康康在学习了矩形定义及判定定理1后,继续探究其它判定定理.
(1)实践与操作
①任意作两条相交的直线,交点记为O;
②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段;OA,OB,OC,OD
③顺次连结所得的四点得到四边形.
于是可以直接判定四边形是平行四边形,则该判定定理是:______.
(2)猜想与证明
通过和同伴交流,他们一致认为四边形是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.
已知:如图,四边形是平行四边形,.
求证:四边形是矩形.
19.小明的书桌上有一个L型台灯,灯柱高,他发现当灯带与水平线夹角为时(图1),灯带的直射宽(,)为,但此时灯的直射宽度不够,当他把灯带调整到与水平线夹角为时(图2),直射宽度刚好合适,求此时台灯最高点C到桌面的距离.(结果保留1位小数)(,,)
20.某酒店有A,B两种客房、其中A种24间,B种20间.若全部入住,一天营业额为7200元;若A,B两种客房均有10间入住,一天营业额为3200元.
(1)求A,B两种客房每间定价分别是多少元?
(2)酒店对A种客房调研发现:如果客房不调价,房间可全部住满;如果每个房间定价每增加10元,就会有一个房间空闲;当A种客房每间定价为多少元时,A种客房一天的营业额W最大,最大营业额为多少元?
21.已知关于x的一元二次方程.
(1)求证:无论m取何值,方程都有两个不相等的实数根;
(2)如果方程的两个实数根为,,且,求m的值.
22.遂宁市作为全国旅游城市,有众多著名景点,为了解“五一”假期同学们的出游情况,某实践探究小组对部分同学假期旅游地做了调查,以下是调查报告的部分内容,请完善报告:
xx小组关于xx学校学生“五一”出游情况调查报告
数据收集
调查方式 抽样调查 调查对象 xx学校学生
数据的整理与描述
景点 A:中国死海 B:龙凤古镇 C:灵泉风景区 D:金华山 E:未出游 F:其他
数据分析及运用
(1)本次被抽样调查的学生总人数为______,扇形统计图中,______,“B:龙凤古镇”对应圆心角的度数是______; (2)请补全条形统计图; (3)该学校总人数为1800人,请你估计该学校学生“五一”假期未出游的人数; (4)未出游中的甲、乙两位同学计划下次假期从A、B、C、D四个景点中任选一个景点旅游,请用树状图或列表的方法求出他们选择同一景点的概率.
23.如图,一次函数的图象与反比例函数的图象相交于,两点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象直接写出时,x的取值范围;
(3)过点B作直线OB,交反比例函数图象于点C,连结AC,求的面积.
24.如图,是的直径,是一条弦,点D是的中点,于点E,交于点F,连结交于点G.
(1)求证:;
(2)延长至点M,使,连结.
①求证:是的切线;
②若,,求的半径.
25.二次函数的图象与x轴分别交于点,,与y轴交于点,P,Q为抛物线上的两点.
(1)求二次函数的表达式;
(2)当P,C两点关于抛物线对轴对称,是以点P为直角顶点的直角三角形时,求点Q的坐标;
(3)设P的横坐标为m,Q的横坐标为,试探究:的面积S是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
参考答案
1.答案:C
解析:,,0都是有理数,是无理数,故选:C.
2.答案:A
解析:由实物图可知,从正面看到的图形是,故选:A.
3.答案:C
解析:万,故选:C.
4.答案:D
解析:A、,该选项错误,不合题意;
B、,该选项错误,不合题意;
C、,该选项错误,不合题意;
D、,该选项正确,符合题意;
故选:D.
5.答案:B
解析:,由①得,,由②得,,不等式组的解集为,不等式组的解集在数轴上表示为,故选:B.
6.答案:C
解析:设这个正多边形的边数为n,则,,这个正多边形的每个外角为,故选:C.
7.答案:B
解析:方程两边同时乘以得,,解得,分式方程的解为正数,,,又,即,,m的取值范围为且,故选:B.
8.答案:A
解析:过点O作于D,则,,
圆的直径为2米,,在中,,,为等边三角形,,淤泥横截面的面积,故选:A.
9.答案:D
解析:,,在和中,,,,在,中,,,,在,中,,,,在,中,,,,综上所述,共有4对“伪全等三角形”,故选:D.
10.答案:B
解析:由图可知,
抛物线的对称轴为直线,且该抛物线与x轴交于点,
,,
则,
抛物线与y轴的交点B在,之间,
,
则,故①错误;
设抛物线与x轴另一个交点,
对称轴为直线,且该抛物线与x轴交于点,
,解得,
则,故②错误;
,,,
,解得,故③正确;
根据抛物线与x轴交于点和,直线过点和,如图,
方程两根为m,n满足,故④正确;
故选:B.
11.答案:
解析:.故答案为:.
12.答案:四
解析:反比例函数的图象在第一、三象限,,,点在第四象限,故答案为:四.
13.答案:甲
解析:甲的平均数为,,乙的平均数为,,,甲成绩更稳定,应选甲参加比赛,
故答案为:甲.
14.答案:
解析:根据题意可得,当时,,则当时,,故答案为:.
15.答案:①②③
解析:如图所示,
E为的中点,,设正方形的边长为,则,折叠,,,,,是等腰三角形,故①正确;
设,,,,,又,四边形是平行四边形,,,即F是的中点,故②正确;
,,,在中,,,,设,则,,,,,,故③正确;
连接,如图所示,
,,,又,,,又,,,又,,,,,,在中,,,故④不正确,故答案为:①②③.
16.答案:2024
解析:
.
17.答案:2
解析:
,
,2,
当时,原式.
18.答案:(1)对角线互相平分的四边形是平行四边形
(2)证明见解析
解析:(1)由作图可得:,,
四边形是平行四边形,
(2)四边形是平行四边形,
,,
,
,,
,
,
四边形是矩形.
19.答案:此时台灯最高点C到桌面的距离为
解析:由已知,,
在图1中,,
,
,
四边形是平行四边形,
,
在中,,
在图2中,过点C作于点N,
,
灯柱高,
点C到桌面的距离为.
答:此时台灯最高点C到桌面的距离为.
20.答案:(1)A种客房每间定价为元,B种客房每间定价为元
(2)当A种客房每间定价为元时,A种客房一天的营业额W最大,最大营业额为元
解析:(1)设A种客房每间定价为x元,B种客房每间定价为y元,
由题意可得,,
解得,
答:A种客房每间定价为元,B种客房每间定价为元;
(2)设A种客房每间定价为a元,
则,
,
当时,W取最大值,元,
答:当A种客房每间定价为元时,A种客房一天的营业额W最大,最大营业额为元.
21.答案:(1)证明见解析
(2)或
解析:(1)证明:,
无论m取何值,,恒成立,
无论m取何值,方程都有两个不相等的实数根.
(2),是方程的两个实数根,
,,
,
解得:或.
22.答案:(1),10,
(2)见解析
(3)
(4)
解析:(1)本次被抽样调查的学生总人数为,
C组的人数为:,
,
,
B:龙凤古镇”对应圆心角的度数是.
故答案为:,10,.
(2)根据(1)可得C组人数为10人,补全统计图,如图所示,
(3).
答:请你估计该学校学生“五一”假期未出游的人数为人;
(4)列表如下,
A B C D
A
B
C
D
共有16种等可能结果,其中他们选择同一景点的情形有4种,
他们选择同一景点的概率为.
23.答案:(1)反比例函数表达式为,一次函数表达式为
(2)或
(3)8
解析:(1)把代入得,,,反比例函数表达式为,把代入得,,,,把、代入得,,解得,一次函数表达式为;
(2)由图象可得,当时,x的取值范围为或;
(3)如图,设直线与y轴相交于点D,过点A作轴于点M,过点C作轴于点N,则,,
点B、C关于原点对称,,,,,,即的面积为8.
24.答案:(1)证明见解析
(2)①证明见解析,②的半径为
解析:(1)证明:如图,连接,
点D是的中点,,,,为的直径,,,,.
(2)证明:①为的直径,,,,是的垂直平分线,,,,而,,,
,为的直径,是的切线;
②,,,,,,,,,,,,的半径为.
25.答案:(1)
(2)
(3)存在,最小值为
解析:(1)把,,代入得,,解得,二次函数的表达式为;
(2)如图:
由得抛物线对称轴为直线,P,C两点关于抛物线对轴对称,,,设,,,,整理得,,解得,(舍去),,;
(3)存在,理由:当点P、Q在x轴下方,且点Q在点P上方时,设点,则点,设直线交x轴于点H,
设直线表达式为:,代入,,得:,解得:,直线的表达式为:,令,得,则,则,则,即S存在最小值为;当点P、Q在x轴下方,且点P在点Q上方时,
同上可求直线表达式为:,令,得,则,则,则即S存在最小值为;当点P、Q都在x轴上方或者一个在x轴上方,一个在x轴下方同理可求,即S存在最小值为,综上所述,的面积S是否存在最小值,且为.
同课章节目录
