1.2我们周围的“数”课件(北京课改版七年级上)
文档属性
| 名称 | 1.2我们周围的“数”课件(北京课改版七年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 153.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览





文档简介
课件13张PPT。走进数学世界1.2我们周围的“数” 京B53467 车牌中的学问想一想(1) 当“京B”后面的五个数位上
都是数字时,可以有多少个不同
的汽车牌照号?牌照号从00000到99999
可供100000辆汽车使用. 车牌中的学问想一想京B53467(2)现在北京市一些汽车牌照号
五个数位中,后四位上都是数字,
而第一个数位上有数字,有大写
英文字母.你知道为什么这样做吗?不同的汽车牌号数将增加
京B53467 车牌中的学问想一想 (3)这样做以后,最多可以有多少个不同的汽车牌照号? 不同的汽车牌号数将增加到
36×10000=360000九宫图 将1,2,3,…,9这九个
数字分别填入图中的九个方格内,
使每行、每列和对角线上的三个
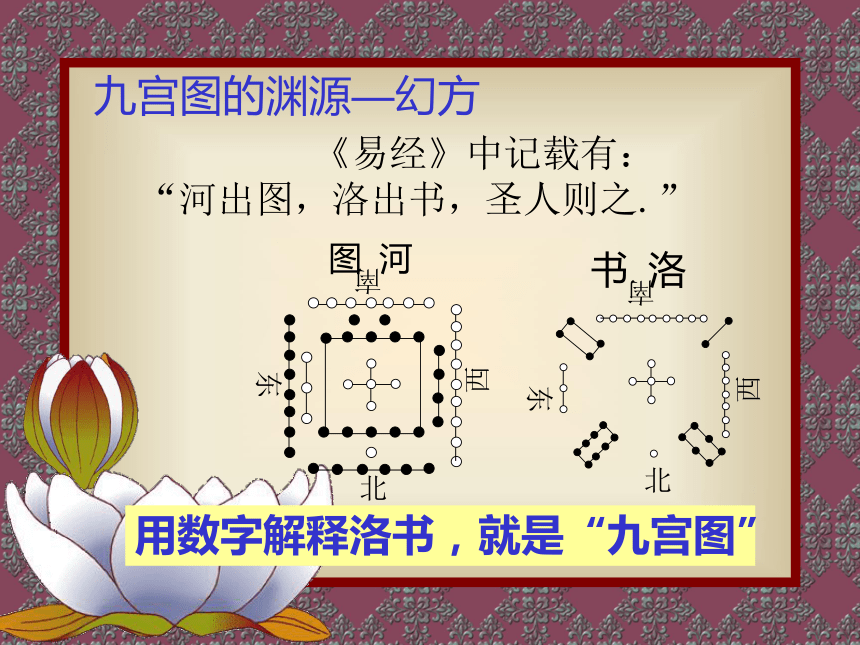
格内的数字之和分别等于15. 怎样完成这个游戏?试一试?????????5 《易经》中记载有: “河出图,洛出书,圣人则之.” 九宫图的渊源—幻方 用数字解释洛书,就是“九宫图” 在6世纪,北周的数学家甄鸾 就是这样描述它的:“九宫者, 二四为肩,六八为足,左三右七, 戴九履一,五居中央.” 123456789二四为肩六八为足左三右七填法 之一到了1275年,南宋的数学家杨辉 在《续古摘奇算法》中介绍了 “九宫图”的填法:“九子斜排,123456789 上下对易,左右相更,四维挺出.” 填法 之二 在4世纪时才有希腊人关于 “4阶”纵横图的记载,9世纪时 才有伊拉克人柯拉(Korra)来 研究纵横图.在欧洲,到了1514年 才出现了第一幅完整的纵横图. 4阶纵横图想一想:你能根据提示在图中填出 “4阶”纵横图吗?123456789101112131415161.把1-16依次排列 提示: 2.把箭头所指的 两数互易 3.填写结果 每行每列的数字之和是 ?34试一试选择几种圆形的物体,想办法 度量它们的直径与周长,并填写下表: 人类为了探求圆周率究竟 是什么数,付出了长期艰苦的 努力.我国古代著名数学家祖 冲之(公元429—公元500) 在计算工具十分简陋的年代,将圆周率 确定在3.1415926到3.1415927之间,
这个精确到小数点后面7位的数值在 世界上领先了1000多年,是中国古代 数学家对人类文明的重大贡献.有关“数”的历史—圆周率课堂小结1. 我们的生活离不开“数”2.“数”可以做游戏3.“数”可以做实验4.中国古代数学家对人类 文明做出重大贡献.
格内的数字之和分别等于15. 怎样完成这个游戏?试一试?????????5 《易经》中记载有: “河出图,洛出书,圣人则之.” 九宫图的渊源—幻方 用数字解释洛书,就是“九宫图” 在6世纪,北周的数学家甄鸾 就是这样描述它的:“九宫者, 二四为肩,六八为足,左三右七, 戴九履一,五居中央.” 123456789二四为肩六八为足左三右七填法 之一到了1275年,南宋的数学家杨辉 在《续古摘奇算法》中介绍了 “九宫图”的填法:“九子斜排,123456789 上下对易,左右相更,四维挺出.” 填法 之二 在4世纪时才有希腊人关于 “4阶”纵横图的记载,9世纪时 才有伊拉克人柯拉(Korra)来 研究纵横图.在欧洲,到了1514年 才出现了第一幅完整的纵横图. 4阶纵横图想一想:你能根据提示在图中填出 “4阶”纵横图吗?123456789101112131415161.把1-16依次排列 提示: 2.把箭头所指的 两数互易 3.填写结果 每行每列的数字之和是 ?34试一试选择几种圆形的物体,想办法 度量它们的直径与周长,并填写下表: 人类为了探求圆周率究竟 是什么数,付出了长期艰苦的 努力.我国古代著名数学家祖 冲之(公元429—公元500) 在计算工具十分简陋的年代,将圆周率 确定在3.1415926到3.1415927之间,
这个精确到小数点后面7位的数值在 世界上领先了1000多年,是中国古代 数学家对人类文明的重大贡献.有关“数”的历史—圆周率课堂小结1. 我们的生活离不开“数”2.“数”可以做游戏3.“数”可以做实验4.中国古代数学家对人类 文明做出重大贡献.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
