2025北师大版高中数学必修第一册同步练习题--§3 用样本估计总体的分布(含解析)
文档属性
| 名称 | 2025北师大版高中数学必修第一册同步练习题--§3 用样本估计总体的分布(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第一册
第六章 统计
§3 用样本估计总体的分布
基础过关练
题组一 统计图表
1.(多选题)(2024浙江杭州富阳实验中学考试)航海模型项目在我国已开展四十余年,深受青少年的喜爱.该项目整合国防、科技、工程、艺术、物理、数学等知识,主要通过让参赛选手制作并遥控各类船只、舰艇等模型,普及船艇知识,探究海洋奥秘,助力培养未来海洋强国的建设者.某学校为了解学生对航海模型项目的喜爱程度,用分层随机抽样法从该校高一、高二、高三年级所有学生中抽取部分学生进行抽样调查.已知该校高一、高二、高三年级学生人数的比例如图所示,若抽取的样本中高三年级学生有32人,则下列说法正确的是( )
A.该校高一年级学生人数是2 000
B.样本中高二年级学生人数是28
C.样本中高三年级学生比高一多12人
D.该校学生总人数是8 000
2.根据甲、乙两名学生的数学学科核心素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象能力指标值为4,乙的数学抽象能力指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力指标值优于甲的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
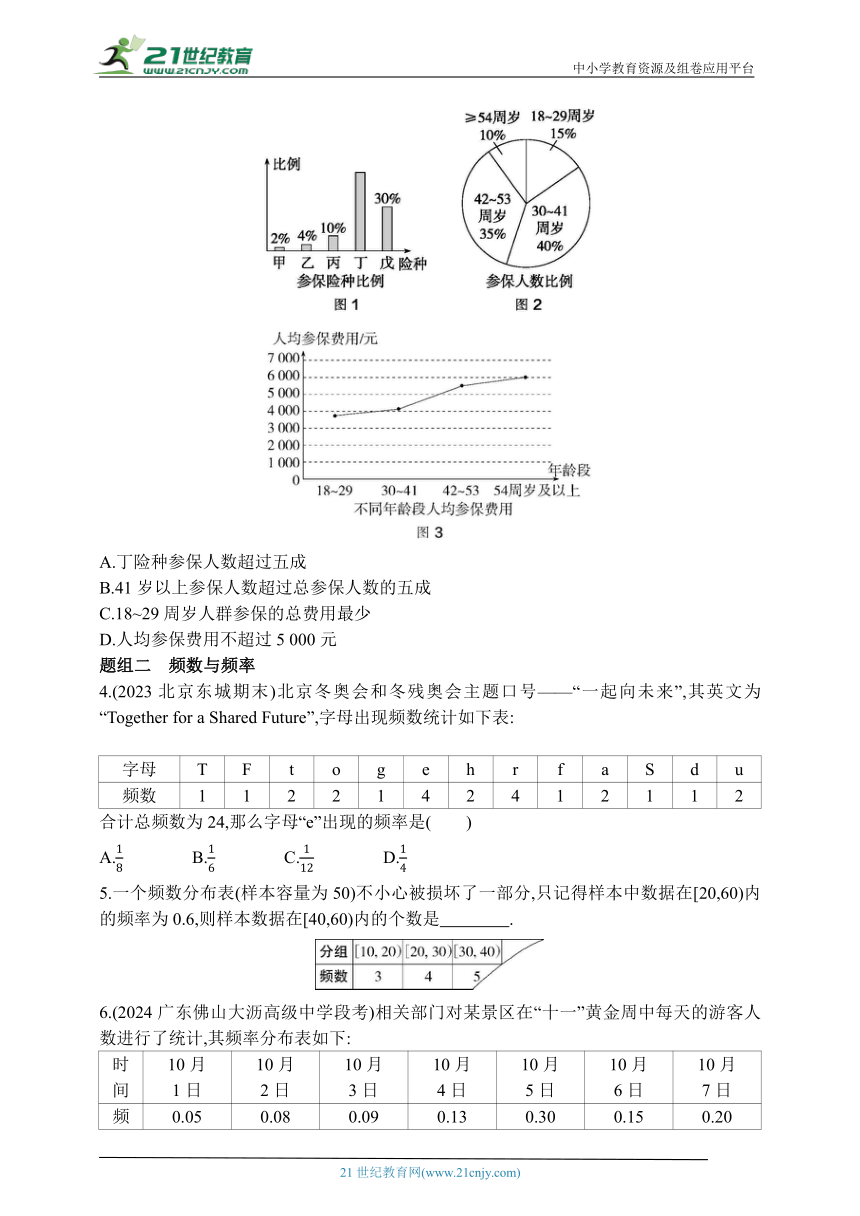
3.(多选题)(2024湖北咸宁赤壁一中月考)某保险公司为客户定制了5个险种:甲,一年期短期;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得到如图所示的统计图,则( )
A.丁险种参保人数超过五成
B.41岁以上参保人数超过总参保人数的五成
C.18~29周岁人群参保的总费用最少
D.人均参保费用不超过5 000元
题组二 频数与频率
4.(2023北京东城期末)北京冬奥会和冬残奥会主题口号——“一起向未来”,其英文为“Together for a Shared Future”,字母出现频数统计如下表:
字母 T F t o g e h r f a S d u
频数 1 1 2 2 1 4 2 4 1 2 1 1 2
合计总频数为24,那么字母“e”出现的频率是( )
A. B. C. D.
5.一个频数分布表(样本容量为50)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.6,则样本数据在[40,60)内的个数是 .
6.(2024广东佛山大沥高级中学段考)相关部门对某景区在“十一”黄金周中每天的游客人数进行了统计,其频率分布表如下:
时 间 10月 1日 10月 2日 10月 3日 10月 4日 10月 5日 10月 6日 10月 7日
频 率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为 万元.
题组三 频率分布直方图
7.(2024山东胶州实验中学月考)某社会调查机构就某地10 000名居民的月收入情况进行了调查,并根据所得数据绘制了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层随机抽样方法抽出200人进行进一步调查,则在月收入为[2 500,3 000)(单位:元)段中抽取的人数是( )
A.100 B.50 C.40 D.25
8.(多选题)某学校为了调查学生在放学后体育运动的情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中体育运动时间(分钟)在[40,50)内的有72人,则下列说法正确的是( )
A.样本中放学后体育运动时间在[40,50)内的频率为0.36
B.样本中放学后体育运动时间不少于40分钟的人数为132
C.n的值为200
D.若该校有1 000名学生,则必定有300人放学后体育运动时间在[50,60]内
9.(2022陕西榆林月考)现对某类文物进行某种物性指标检测,从1 000件中随机抽取了200件,测量该物性指标值,得到如下频率分布直方图,据此估计这1 000件文物中该物性指标值不小于95的件数为 .
10.(2023江西贵溪一中月考)某高校在2022年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下.
分组 频数 频率
第1组 [160,165) 5 0.050
第2组 [165,170) m 0.350
第3组 [170,175) n p
第4组 [175,180) 20 0.200
第5组 [180,185] 10 0.100
合计 100 1.000
(1)求频率分布表中m,n,p的值,并将相应的频率分布直方图补充完整;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩较高的第3,4,5组中用分层随机抽样的方法抽取6名学生进入第二轮面试,则第3,4,5组各抽取多少名学生进入第二轮面试
题组四 频率折线图
11.(2022江西吉水中学月考)为了了解某外贸企业职工对“一带一路”的认知程度,随机抽取了110名职工组织“一带一路”知识竞赛,满分为100分(80分及以上为认知程度较高),并将所得成绩分组得到了如图所示的频率折线图.从频率折线图中得到的这110名职工成绩的以下信息正确的是( )
A.成绩是100分的人数比成绩是50分的人数多
B.对“一带一路”认知程度较高的人数是40
C.成绩是75分的人数为40
D.成绩落在[70,80)内的人数为20
12.某学校对100间学生公寓的卫生情况进行综合评比,依考核分数分为A,B,C,D四个等级.其中分数在[60,70)内的为D等级;分数在[70,80)内的为C等级;分数在[80,90)内的为B等级;分数在[90,100]内的为A等级.考核评估后,得其频率折线图如图所示,估计这100间学生公寓考核分数为C,D等级的比考核分数为A,B等级的多多少.
能力提升练
题组一 统计图表的综合应用
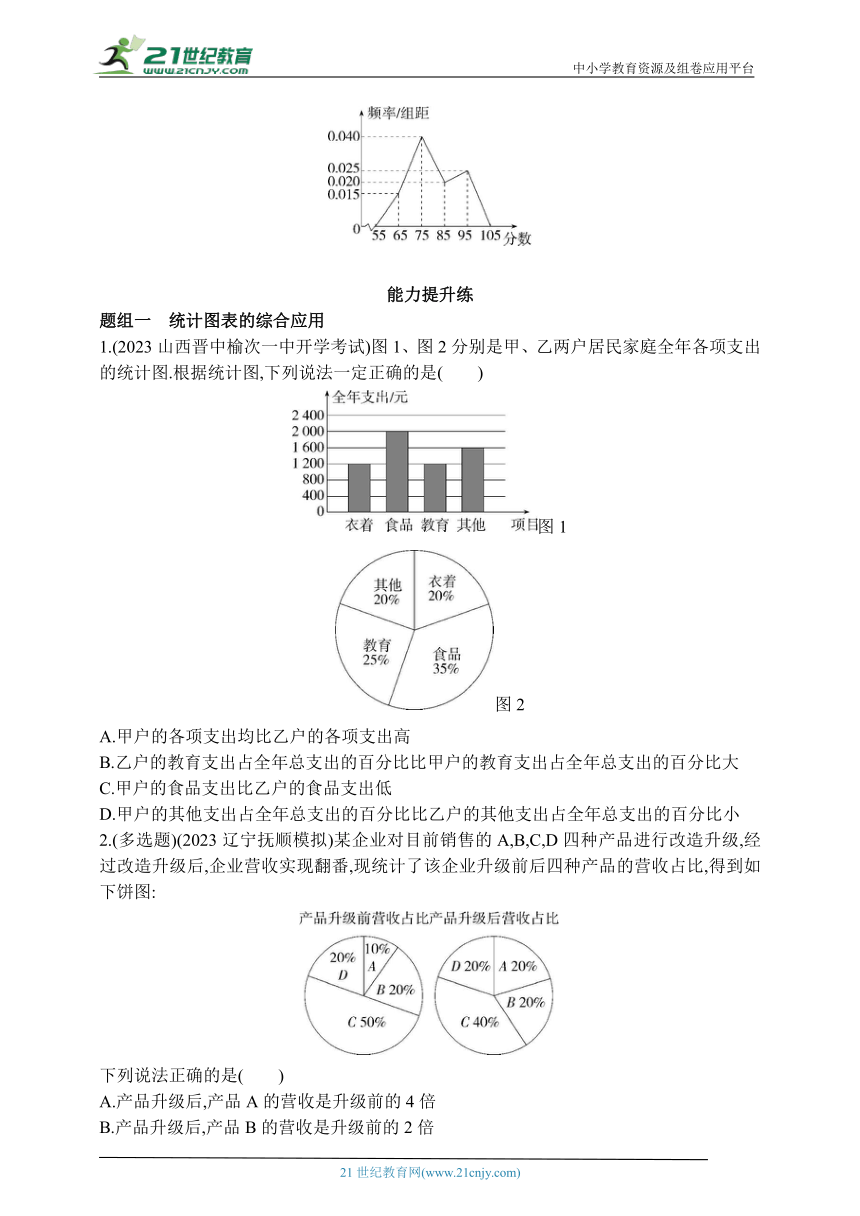
1.(2023山西晋中榆次一中开学考试)图1、图2分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列说法一定正确的是( )
图1
图2
A.甲户的各项支出均比乙户的各项支出高
B.乙户的教育支出占全年总支出的百分比比甲户的教育支出占全年总支出的百分比大
C.甲户的食品支出比乙户的食品支出低
D.甲户的其他支出占全年总支出的百分比比乙户的其他支出占全年总支出的百分比小
2.(多选题)(2023辽宁抚顺模拟)某企业对目前销售的A,B,C,D四种产品进行改造升级,经过改造升级后,企业营收实现翻番,现统计了该企业升级前后四种产品的营收占比,得到如下饼图:
下列说法正确的是( )
A.产品升级后,产品A的营收是升级前的4倍
B.产品升级后,产品B的营收是升级前的2倍
C.产品升级后,产品C的营收减少
D.产品升级后,产品B,D的营收总和占总营收的比例不变
3.对某种灯泡随机地抽取200个样品进行使用寿命调查,结果如下:
使用寿命/天 频数 频率
[100,200) 20 0.10
[200,300) 30 y
[300,400) 70 0.35
[400,500) x 0.15
[500,600] 50 0.25
合计 200 1.00
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天的是次品,其余的是正品.某人从这种灯泡中随机购买了n(n∈N+)个,若这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层随机抽样所得的结果相同,则n的最小值为( )
A.2 B.3 C.4 D.5
4.(2022江苏新海高级中学期末)2022年2月28日,国家统计局发布了我国2021年国民经济和社会发展统计公报,2021年全国居民人均可支配收入和消费支出较上一年均有所增长,结合如下统计图,下列说法中错误的是( )
A.2017—2021年全国居民人均可支配收入逐年递增
B.2021年全国居民人均消费支出构成中教育文化娱乐占比高于医疗保健占比
C.2020年全国居民人均可支配收入较上一年下降
D.2021年全国居民人均消费支出构成中食品烟酒和居住占比之和超过50%
题组二 频率分布直方图的综合应用
5.某班同学进行社会实践,对年龄(单位:岁)在[25,55]内的人群随机抽取n人进行了生活习惯是否符合低碳观念的调查,生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图,则表中p,a的值分别为( )
组别 分组 “低碳族” 的人数 “低碳族”占本组 的频率
第一组 [25,30) 120 0.6
第二组 [30,35) 195 p
第三组 [35,40) 100 0.5
第四组 [40,45) a 0.4
第五组 [45,50) 30 0.3
第六组 [50,55] 15 0.3
A.0.79,20 B.0.195,40
C.0.65,60 D.0.975,80
6.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重的数据整理后,画出了如图所示的频率分布直方图,已知图中从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,若全校男、女生的人数之比为3∶2,则全校抽取的学生人数为 .
7.(2023云南名校月考)某市某次高中数学统测学生测试成绩频率分布直方图如图所示.现按测试成绩由高到低分成A,B,C,D四个等级,其中A等级占25%,B等级占40%,C等级占30%,D等级占5%,规定达到C等级及以上才能通过考试,则要通过本次考试,学生的成绩至少为 分.
8.(2024江西上饶广丰一中月考)为了了解某工厂生产的产品情况,从该工厂生产的产品中随机抽取了一个容量为200的样本,测量它们的尺寸(单位:mm),并将数据分为[92,94),[94,96),[96,98),[98,100),[100,102),[102,104),[104,106]七组,其频率分布直方图如图所示.
(1)求图中x的值;
(2)求200件样本中尺寸在[98,100)(单位:mm)内的样本件数;
(3)记产品尺寸在[98,102)(单位:mm)内的为A等品,每件可获利5元;产品尺寸在[92,94)(单位:mm)内的为不合格品,每件亏损2元;其余为合格品,每件可获利3元.若该工厂一个月共生产3 000件产品,以样本的频率代替总体在各组内的频率,若单月利润未能达到11 000元,则需要对该工厂设备实施升级改造,试判断是否需要对该工厂设备实施升级改造.
9.(2023北京丰台期末)某商场为了制订合理的停车收费政策,需要了解顾客的停车时长(单位:分钟).现随机抽取了该商场到访顾客的100辆车进行调查,将数据分成6组:(0,100],(100,200],(200,300],(300,400],(400,500],(500,600],并整理得到如下频率分布直方图:
(1)求样本中停车时长在区间(400,500]内的频率;
(2)若某天该商场到访顾客的车辆数为1 000,根据频率分布直方图估计该天停车时长在区间(100,400]内的车辆数;
(3)为了吸引顾客,该商场准备给停车时长较短的车辆提供免费停车服务.若使该服务能够惠及25%的到访顾客的车辆,请你根据频率分布直方图,给出确定免费停车时长标准的建议.
答案与分层梯度式解析
第六章 统计
§3 用样本估计总体的分布
基础过关练
1.BC 由题图可知高三年级学生人数占总人数的40%,抽取的样本中高三年级学生有32人,
则抽取的学生总人数为=80,
则样本中高一年级学生人数为80×25%=20,高二年级学生人数为80×35%=28,
故样本中高三年级学生比高一多32-20=12(人),故B,C正确;
因为样本容量为80,但抽取的比例不知道,所以该校高一年级学生人数和该校学生总人数不可求,故A,D错误.故选BC.
2.C 依题意,乙的逻辑推理能力指标值为3,而甲的逻辑推理能力指标值为4,故A错误;
甲的数学建模能力指标值为3,而乙的直观想象能力指标值为5,故B错误;
乙的六维能力指标值之和为24,甲的六维能力指标值之和为23,故C正确;
甲的数学运算能力指标值为4,而甲的直观想象能力指标值为5,故D错误.
3.ACD 由题图1可知,丁险种参保人数所占比例为1-2%-4%-10%-30%=54%,超过五成,故A正确;
由题图2可知,41岁以上参保人数所占比例为35%+10%=45%,不到五成,故B错误;
由题图2与题图3可知,18~29周岁参保人数所占比例为15%,人均参保费用在区间(3 000,4 000)(单位:元)内,54周岁及以上参保人数所占比例最少,为10%,人均参保费用为6 000元,所以18~29周岁人群参保的总费用最少,故C正确;
由题图2与题图3可知,人均参保费用不超过5 000元,故D正确.
故选ACD.
4.B 由题中表格可知,字母“e”出现的频数为4,又合计总频数为24,所以字母“e”出现的频率为.故选B.
5.答案 21
解析 由已知可得样本中数据在[20,60)内的频数为50×0.6=30,故样本数据在[40,60)内的个数为30-4-5=21.
6.答案 48
解析 设游客人数最多的那一天的营业额约为x万元,则,解得x=48.
7.B 月收入在[2 500,3 000)(单位:元)内的频率为0.000 5×500=0.25,故在该段抽取的人数为200×0.25=50.故选B.
8.ABC 由题中频率分布直方图得样本中放学后体育运动时间在[40,50)内的频率是1-(0.01+0.024+0.03)×10=0.36,A正确;n==200,C正确;样本中放学后体育运动时间不少于40分钟的人数为200×(0.36+0.3)=132,B正确;若该校有1 000名学生,则1 000×0.3=300,用样本估计总体,只能说明可能有300人放学后体育运动时间在[50,60]内,D错误.
9.答案 670
解析 抽取的200件文物中,该物性指标值不小于95的频率为(0.033+0.024+0.008+0.002)×10=0.67,
由此估计出1 000件文物中该物性指标值不小于95的频率为0.67,
故估计这1 000件文物中该物性指标值不小于95的有1 000×0.67=670(件).
10.解析 (1)由已知得0.050+0.350+p+0.200+0.100=1.000,解得p=0.300,
m=0.35×100=35,n=0.3×100=30,
补全频率分布直方图如图所示:
(2)第3,4,5组的人数之比为30∶20∶10,即3∶2∶1,现用分层随机抽样的方法选6名学生,故第3,4,5组应抽取的学生人数分别为3,2,1.
11.B 由于频率折线图表示的是某一范围的频率,所以从频率折线图看不出成绩是100分的人数多还是成绩是50分的人数多,也不能得出成绩是75分的人数,故A,C错误;
对于B,成绩为80分及以上的人数为×10×110=40,故B正确;
对于D,成绩落在[70,80)内的人数为10××110=40,故D错误.
故选B.
12.解析 由题中频率折线图可知,分数为A等级的频率为0.025×10=0.25,分数为B等级的频率为0.020×10=0.20,分数为C等级的频率为0.040×10=0.40,分数为D等级的频率为0.015×10=0.15,所以估计这100间学生公寓考核分数为C,D等级的比考核分数为A,B等级的多100×(0.40+0.15)-100×(0.25+0.20)=10(间).
能力提升练
1.B 由题图2无法确定乙户的各项支出,故无法比较甲、乙的各项支出,故A,C错误;
对于B,乙户的教育支出占全年总支出的百分比为25%,甲户的教育支出占全年总支出的百分比为×100%=20%,故B正确;
对于D,甲户的其他支出占全年总支出的百分比为×100%≈26.7%,乙户的其他支出占全年总支出的百分比为20%,故D错误.
故选B.
2.ABD 设产品升级前的总营收为a,则产品升级后的总营收为2a.
对于产品A,产品升级前的营收为0.1a,升级后的营收为2a×0.2=0.4a,故升级后的产品A的营收是升级前的4倍,A正确.
对于产品B,产品升级前的营收为0.2a,升级后的营收为2a×0.2=0.4a,故升级后的产品B的营收是升级前的2倍,B正确.
对于产品C,产品升级前的营收为0.5a,升级后的营收为2a×0.4=0.8a,故升级后的产品C的营收增加,C错误.
产品升级前后,产品B,D的营收总和占总营收的比例均为20%+20%=40%,不变,D正确.
故选ABD.
3.C 由题中频率分布表,得x=200×0.15=30,灯泡样品中优等品有50个,次品有20+30=50(个),则正品有200-50-50=100(个),∴优等品、正品、次品的比为50∶100∶50,即1∶2∶1,∴按分层随机抽样的方法,购买灯泡的个数n=k+2k+k=4k(k∈N+),∴n的最小值为4.故选C.
4.C 观察题图1可知2017—2021年全国居民人均可支配收入逐年递增,2020年全国居民人均可支配收入较上一年增长了2.1%,故A中说法正确,C中说法错误;
观察题图2可知2021年全国居民人均消费支出构成中教育文化娱乐占比为10.8%,医疗保健占比为8.8%,食品烟酒和居住占比之和为29.8%+23.4%=53.2%,超过50%,故B,D中说法均正确.故选C.
5.C 第一组的人数为120÷0.6=200,第三组的人数为100÷0.5=200,第五组的人数为30÷0.3=100,第六组的人数为15÷0.3=50,
由题中的频率分布直方图可得第一组的频率为5×0.04=0.2,所以n==1 000,
所以第四组的人数为5×0.03×1 000=150,所以a=150×0.4=60,第二组的人数为1 000-(200+200+150+100+50)=300,所以p==0.65.故选C.
6.答案 80
解析 由题图得,第四小组与第五小组的频率之和为(0.037 5+0.012 5)×5=0.25.
因为从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,
所以前三个小组的频数之和为36,所以抽取的男生人数为=48.
因为全校男、女生的人数之比为3∶2,所以全校抽取的学生人数为48×=80.
7.答案 24
解析 由题图可知,分数低于20的频率为0.001×20=0.02,低于40的频率为(0.001+0.007 5)×20=0.17,因此通过本次考试的分数线位于[20,40),则20+20×=24,所以要通过本次考试,学生的成绩至少为24分.
8.解析 (1)由题意得(0.02+0.04+0.06+0.07+0.09+0.10+x)×2=1,解得x=0.12.
(2)200件样本中尺寸在[98,100)内的样本件数为200×0.09×2=36.
(3)由题意可得,这批产品中A等品有3 000×(0.18+0.20)=1 140(件),
不合格品有3 000×0.04=120(件),
合格品有3 000-1 140-120=1 740(件),
1 140×5+1 740×3-120×2=10 680(元).
则该工厂生产的产品一个月所获得的利润为10 680元,
因为10 680<11 000,所以需要对该工厂设备实施升级改造.
9.解析 (1)设样本中停车时长在区间(400,500]内的频率为x,由题意得(0.000 2+0.001 3+0.001 6+0.003 2+0.003 4)×100+x=1,解得x=0.03.所以样本中停车时长在区间(400,500]内的频率为0.03.
(2)根据题中频率分布直方图可知停车时长在区间(100,400]内的频率为(0.003 2+0.003 4+0.001 6)×100=0.82,所以估计该天停车时长在区间(100,400]内的车辆数为0.82×1 000=820.
(3)因为停车时长在(0,100]内的频率为0.13,停车时长在(0,200]内的频率为0.45,所以免费停车时长标准在(100,200]内,设免费停车时长标准为y分钟,则0.13+(y-100)×0.003 2=0.25,解得y=137.5.
故免费停车时长标准定为137.5分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第一册
第六章 统计
§3 用样本估计总体的分布
基础过关练
题组一 统计图表
1.(多选题)(2024浙江杭州富阳实验中学考试)航海模型项目在我国已开展四十余年,深受青少年的喜爱.该项目整合国防、科技、工程、艺术、物理、数学等知识,主要通过让参赛选手制作并遥控各类船只、舰艇等模型,普及船艇知识,探究海洋奥秘,助力培养未来海洋强国的建设者.某学校为了解学生对航海模型项目的喜爱程度,用分层随机抽样法从该校高一、高二、高三年级所有学生中抽取部分学生进行抽样调查.已知该校高一、高二、高三年级学生人数的比例如图所示,若抽取的样本中高三年级学生有32人,则下列说法正确的是( )
A.该校高一年级学生人数是2 000
B.样本中高二年级学生人数是28
C.样本中高三年级学生比高一多12人
D.该校学生总人数是8 000
2.根据甲、乙两名学生的数学学科核心素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象能力指标值为4,乙的数学抽象能力指标值为5,则下面叙述正确的是( )
A.乙的逻辑推理能力指标值优于甲的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
3.(多选题)(2024湖北咸宁赤壁一中月考)某保险公司为客户定制了5个险种:甲,一年期短期;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得到如图所示的统计图,则( )
A.丁险种参保人数超过五成
B.41岁以上参保人数超过总参保人数的五成
C.18~29周岁人群参保的总费用最少
D.人均参保费用不超过5 000元
题组二 频数与频率
4.(2023北京东城期末)北京冬奥会和冬残奥会主题口号——“一起向未来”,其英文为“Together for a Shared Future”,字母出现频数统计如下表:
字母 T F t o g e h r f a S d u
频数 1 1 2 2 1 4 2 4 1 2 1 1 2
合计总频数为24,那么字母“e”出现的频率是( )
A. B. C. D.
5.一个频数分布表(样本容量为50)不小心被损坏了一部分,只记得样本中数据在[20,60)内的频率为0.6,则样本数据在[40,60)内的个数是 .
6.(2024广东佛山大沥高级中学段考)相关部门对某景区在“十一”黄金周中每天的游客人数进行了统计,其频率分布表如下:
时 间 10月 1日 10月 2日 10月 3日 10月 4日 10月 5日 10月 6日 10月 7日
频 率 0.05 0.08 0.09 0.13 0.30 0.15 0.20
已知10月1日这天该景区的营业额约为8万元,假定这七天每天游客人均消费相同,则这个黄金周该景区游客人数最多的那一天的营业额约为 万元.
题组三 频率分布直方图
7.(2024山东胶州实验中学月考)某社会调查机构就某地10 000名居民的月收入情况进行了调查,并根据所得数据绘制了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层随机抽样方法抽出200人进行进一步调查,则在月收入为[2 500,3 000)(单位:元)段中抽取的人数是( )
A.100 B.50 C.40 D.25
8.(多选题)某学校为了调查学生在放学后体育运动的情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中体育运动时间(分钟)在[40,50)内的有72人,则下列说法正确的是( )
A.样本中放学后体育运动时间在[40,50)内的频率为0.36
B.样本中放学后体育运动时间不少于40分钟的人数为132
C.n的值为200
D.若该校有1 000名学生,则必定有300人放学后体育运动时间在[50,60]内
9.(2022陕西榆林月考)现对某类文物进行某种物性指标检测,从1 000件中随机抽取了200件,测量该物性指标值,得到如下频率分布直方图,据此估计这1 000件文物中该物性指标值不小于95的件数为 .
10.(2023江西贵溪一中月考)某高校在2022年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下.
分组 频数 频率
第1组 [160,165) 5 0.050
第2组 [165,170) m 0.350
第3组 [170,175) n p
第4组 [175,180) 20 0.200
第5组 [180,185] 10 0.100
合计 100 1.000
(1)求频率分布表中m,n,p的值,并将相应的频率分布直方图补充完整;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩较高的第3,4,5组中用分层随机抽样的方法抽取6名学生进入第二轮面试,则第3,4,5组各抽取多少名学生进入第二轮面试
题组四 频率折线图
11.(2022江西吉水中学月考)为了了解某外贸企业职工对“一带一路”的认知程度,随机抽取了110名职工组织“一带一路”知识竞赛,满分为100分(80分及以上为认知程度较高),并将所得成绩分组得到了如图所示的频率折线图.从频率折线图中得到的这110名职工成绩的以下信息正确的是( )
A.成绩是100分的人数比成绩是50分的人数多
B.对“一带一路”认知程度较高的人数是40
C.成绩是75分的人数为40
D.成绩落在[70,80)内的人数为20
12.某学校对100间学生公寓的卫生情况进行综合评比,依考核分数分为A,B,C,D四个等级.其中分数在[60,70)内的为D等级;分数在[70,80)内的为C等级;分数在[80,90)内的为B等级;分数在[90,100]内的为A等级.考核评估后,得其频率折线图如图所示,估计这100间学生公寓考核分数为C,D等级的比考核分数为A,B等级的多多少.
能力提升练
题组一 统计图表的综合应用
1.(2023山西晋中榆次一中开学考试)图1、图2分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图,下列说法一定正确的是( )
图1
图2
A.甲户的各项支出均比乙户的各项支出高
B.乙户的教育支出占全年总支出的百分比比甲户的教育支出占全年总支出的百分比大
C.甲户的食品支出比乙户的食品支出低
D.甲户的其他支出占全年总支出的百分比比乙户的其他支出占全年总支出的百分比小
2.(多选题)(2023辽宁抚顺模拟)某企业对目前销售的A,B,C,D四种产品进行改造升级,经过改造升级后,企业营收实现翻番,现统计了该企业升级前后四种产品的营收占比,得到如下饼图:
下列说法正确的是( )
A.产品升级后,产品A的营收是升级前的4倍
B.产品升级后,产品B的营收是升级前的2倍
C.产品升级后,产品C的营收减少
D.产品升级后,产品B,D的营收总和占总营收的比例不变
3.对某种灯泡随机地抽取200个样品进行使用寿命调查,结果如下:
使用寿命/天 频数 频率
[100,200) 20 0.10
[200,300) 30 y
[300,400) 70 0.35
[400,500) x 0.15
[500,600] 50 0.25
合计 200 1.00
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天的是次品,其余的是正品.某人从这种灯泡中随机购买了n(n∈N+)个,若这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层随机抽样所得的结果相同,则n的最小值为( )
A.2 B.3 C.4 D.5
4.(2022江苏新海高级中学期末)2022年2月28日,国家统计局发布了我国2021年国民经济和社会发展统计公报,2021年全国居民人均可支配收入和消费支出较上一年均有所增长,结合如下统计图,下列说法中错误的是( )
A.2017—2021年全国居民人均可支配收入逐年递增
B.2021年全国居民人均消费支出构成中教育文化娱乐占比高于医疗保健占比
C.2020年全国居民人均可支配收入较上一年下降
D.2021年全国居民人均消费支出构成中食品烟酒和居住占比之和超过50%
题组二 频率分布直方图的综合应用
5.某班同学进行社会实践,对年龄(单位:岁)在[25,55]内的人群随机抽取n人进行了生活习惯是否符合低碳观念的调查,生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图,则表中p,a的值分别为( )
组别 分组 “低碳族” 的人数 “低碳族”占本组 的频率
第一组 [25,30) 120 0.6
第二组 [30,35) 195 p
第三组 [35,40) 100 0.5
第四组 [40,45) a 0.4
第五组 [45,50) 30 0.3
第六组 [50,55] 15 0.3
A.0.79,20 B.0.195,40
C.0.65,60 D.0.975,80
6.为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重的数据整理后,画出了如图所示的频率分布直方图,已知图中从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,若全校男、女生的人数之比为3∶2,则全校抽取的学生人数为 .
7.(2023云南名校月考)某市某次高中数学统测学生测试成绩频率分布直方图如图所示.现按测试成绩由高到低分成A,B,C,D四个等级,其中A等级占25%,B等级占40%,C等级占30%,D等级占5%,规定达到C等级及以上才能通过考试,则要通过本次考试,学生的成绩至少为 分.
8.(2024江西上饶广丰一中月考)为了了解某工厂生产的产品情况,从该工厂生产的产品中随机抽取了一个容量为200的样本,测量它们的尺寸(单位:mm),并将数据分为[92,94),[94,96),[96,98),[98,100),[100,102),[102,104),[104,106]七组,其频率分布直方图如图所示.
(1)求图中x的值;
(2)求200件样本中尺寸在[98,100)(单位:mm)内的样本件数;
(3)记产品尺寸在[98,102)(单位:mm)内的为A等品,每件可获利5元;产品尺寸在[92,94)(单位:mm)内的为不合格品,每件亏损2元;其余为合格品,每件可获利3元.若该工厂一个月共生产3 000件产品,以样本的频率代替总体在各组内的频率,若单月利润未能达到11 000元,则需要对该工厂设备实施升级改造,试判断是否需要对该工厂设备实施升级改造.
9.(2023北京丰台期末)某商场为了制订合理的停车收费政策,需要了解顾客的停车时长(单位:分钟).现随机抽取了该商场到访顾客的100辆车进行调查,将数据分成6组:(0,100],(100,200],(200,300],(300,400],(400,500],(500,600],并整理得到如下频率分布直方图:
(1)求样本中停车时长在区间(400,500]内的频率;
(2)若某天该商场到访顾客的车辆数为1 000,根据频率分布直方图估计该天停车时长在区间(100,400]内的车辆数;
(3)为了吸引顾客,该商场准备给停车时长较短的车辆提供免费停车服务.若使该服务能够惠及25%的到访顾客的车辆,请你根据频率分布直方图,给出确定免费停车时长标准的建议.
答案与分层梯度式解析
第六章 统计
§3 用样本估计总体的分布
基础过关练
1.BC 由题图可知高三年级学生人数占总人数的40%,抽取的样本中高三年级学生有32人,
则抽取的学生总人数为=80,
则样本中高一年级学生人数为80×25%=20,高二年级学生人数为80×35%=28,
故样本中高三年级学生比高一多32-20=12(人),故B,C正确;
因为样本容量为80,但抽取的比例不知道,所以该校高一年级学生人数和该校学生总人数不可求,故A,D错误.故选BC.
2.C 依题意,乙的逻辑推理能力指标值为3,而甲的逻辑推理能力指标值为4,故A错误;
甲的数学建模能力指标值为3,而乙的直观想象能力指标值为5,故B错误;
乙的六维能力指标值之和为24,甲的六维能力指标值之和为23,故C正确;
甲的数学运算能力指标值为4,而甲的直观想象能力指标值为5,故D错误.
3.ACD 由题图1可知,丁险种参保人数所占比例为1-2%-4%-10%-30%=54%,超过五成,故A正确;
由题图2可知,41岁以上参保人数所占比例为35%+10%=45%,不到五成,故B错误;
由题图2与题图3可知,18~29周岁参保人数所占比例为15%,人均参保费用在区间(3 000,4 000)(单位:元)内,54周岁及以上参保人数所占比例最少,为10%,人均参保费用为6 000元,所以18~29周岁人群参保的总费用最少,故C正确;
由题图2与题图3可知,人均参保费用不超过5 000元,故D正确.
故选ACD.
4.B 由题中表格可知,字母“e”出现的频数为4,又合计总频数为24,所以字母“e”出现的频率为.故选B.
5.答案 21
解析 由已知可得样本中数据在[20,60)内的频数为50×0.6=30,故样本数据在[40,60)内的个数为30-4-5=21.
6.答案 48
解析 设游客人数最多的那一天的营业额约为x万元,则,解得x=48.
7.B 月收入在[2 500,3 000)(单位:元)内的频率为0.000 5×500=0.25,故在该段抽取的人数为200×0.25=50.故选B.
8.ABC 由题中频率分布直方图得样本中放学后体育运动时间在[40,50)内的频率是1-(0.01+0.024+0.03)×10=0.36,A正确;n==200,C正确;样本中放学后体育运动时间不少于40分钟的人数为200×(0.36+0.3)=132,B正确;若该校有1 000名学生,则1 000×0.3=300,用样本估计总体,只能说明可能有300人放学后体育运动时间在[50,60]内,D错误.
9.答案 670
解析 抽取的200件文物中,该物性指标值不小于95的频率为(0.033+0.024+0.008+0.002)×10=0.67,
由此估计出1 000件文物中该物性指标值不小于95的频率为0.67,
故估计这1 000件文物中该物性指标值不小于95的有1 000×0.67=670(件).
10.解析 (1)由已知得0.050+0.350+p+0.200+0.100=1.000,解得p=0.300,
m=0.35×100=35,n=0.3×100=30,
补全频率分布直方图如图所示:
(2)第3,4,5组的人数之比为30∶20∶10,即3∶2∶1,现用分层随机抽样的方法选6名学生,故第3,4,5组应抽取的学生人数分别为3,2,1.
11.B 由于频率折线图表示的是某一范围的频率,所以从频率折线图看不出成绩是100分的人数多还是成绩是50分的人数多,也不能得出成绩是75分的人数,故A,C错误;
对于B,成绩为80分及以上的人数为×10×110=40,故B正确;
对于D,成绩落在[70,80)内的人数为10××110=40,故D错误.
故选B.
12.解析 由题中频率折线图可知,分数为A等级的频率为0.025×10=0.25,分数为B等级的频率为0.020×10=0.20,分数为C等级的频率为0.040×10=0.40,分数为D等级的频率为0.015×10=0.15,所以估计这100间学生公寓考核分数为C,D等级的比考核分数为A,B等级的多100×(0.40+0.15)-100×(0.25+0.20)=10(间).
能力提升练
1.B 由题图2无法确定乙户的各项支出,故无法比较甲、乙的各项支出,故A,C错误;
对于B,乙户的教育支出占全年总支出的百分比为25%,甲户的教育支出占全年总支出的百分比为×100%=20%,故B正确;
对于D,甲户的其他支出占全年总支出的百分比为×100%≈26.7%,乙户的其他支出占全年总支出的百分比为20%,故D错误.
故选B.
2.ABD 设产品升级前的总营收为a,则产品升级后的总营收为2a.
对于产品A,产品升级前的营收为0.1a,升级后的营收为2a×0.2=0.4a,故升级后的产品A的营收是升级前的4倍,A正确.
对于产品B,产品升级前的营收为0.2a,升级后的营收为2a×0.2=0.4a,故升级后的产品B的营收是升级前的2倍,B正确.
对于产品C,产品升级前的营收为0.5a,升级后的营收为2a×0.4=0.8a,故升级后的产品C的营收增加,C错误.
产品升级前后,产品B,D的营收总和占总营收的比例均为20%+20%=40%,不变,D正确.
故选ABD.
3.C 由题中频率分布表,得x=200×0.15=30,灯泡样品中优等品有50个,次品有20+30=50(个),则正品有200-50-50=100(个),∴优等品、正品、次品的比为50∶100∶50,即1∶2∶1,∴按分层随机抽样的方法,购买灯泡的个数n=k+2k+k=4k(k∈N+),∴n的最小值为4.故选C.
4.C 观察题图1可知2017—2021年全国居民人均可支配收入逐年递增,2020年全国居民人均可支配收入较上一年增长了2.1%,故A中说法正确,C中说法错误;
观察题图2可知2021年全国居民人均消费支出构成中教育文化娱乐占比为10.8%,医疗保健占比为8.8%,食品烟酒和居住占比之和为29.8%+23.4%=53.2%,超过50%,故B,D中说法均正确.故选C.
5.C 第一组的人数为120÷0.6=200,第三组的人数为100÷0.5=200,第五组的人数为30÷0.3=100,第六组的人数为15÷0.3=50,
由题中的频率分布直方图可得第一组的频率为5×0.04=0.2,所以n==1 000,
所以第四组的人数为5×0.03×1 000=150,所以a=150×0.4=60,第二组的人数为1 000-(200+200+150+100+50)=300,所以p==0.65.故选C.
6.答案 80
解析 由题图得,第四小组与第五小组的频率之和为(0.037 5+0.012 5)×5=0.25.
因为从左到右前三个小组的频率之比为1∶2∶3,第二小组的频数为12,
所以前三个小组的频数之和为36,所以抽取的男生人数为=48.
因为全校男、女生的人数之比为3∶2,所以全校抽取的学生人数为48×=80.
7.答案 24
解析 由题图可知,分数低于20的频率为0.001×20=0.02,低于40的频率为(0.001+0.007 5)×20=0.17,因此通过本次考试的分数线位于[20,40),则20+20×=24,所以要通过本次考试,学生的成绩至少为24分.
8.解析 (1)由题意得(0.02+0.04+0.06+0.07+0.09+0.10+x)×2=1,解得x=0.12.
(2)200件样本中尺寸在[98,100)内的样本件数为200×0.09×2=36.
(3)由题意可得,这批产品中A等品有3 000×(0.18+0.20)=1 140(件),
不合格品有3 000×0.04=120(件),
合格品有3 000-1 140-120=1 740(件),
1 140×5+1 740×3-120×2=10 680(元).
则该工厂生产的产品一个月所获得的利润为10 680元,
因为10 680<11 000,所以需要对该工厂设备实施升级改造.
9.解析 (1)设样本中停车时长在区间(400,500]内的频率为x,由题意得(0.000 2+0.001 3+0.001 6+0.003 2+0.003 4)×100+x=1,解得x=0.03.所以样本中停车时长在区间(400,500]内的频率为0.03.
(2)根据题中频率分布直方图可知停车时长在区间(100,400]内的频率为(0.003 2+0.003 4+0.001 6)×100=0.82,所以估计该天停车时长在区间(100,400]内的车辆数为0.82×1 000=820.
(3)因为停车时长在(0,100]内的频率为0.13,停车时长在(0,200]内的频率为0.45,所以免费停车时长标准在(100,200]内,设免费停车时长标准为y分钟,则0.13+(y-100)×0.003 2=0.25,解得y=137.5.
故免费停车时长标准定为137.5分钟.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
