2025北师大版高中数学必修第一册同步练习题--第六章 统计复习提升(含解析)
文档属性
| 名称 | 2025北师大版高中数学必修第一册同步练习题--第六章 统计复习提升(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 546.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 21:28:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第一册
本章复习提升
易混易错练
易错点1 对分层随机抽样的抽样比理解不准确致错
1.中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气歌”是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气歌”,只能说出春、夏两句的有45人,能说出春、夏、秋三句及以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气歌”只能说出第一句“春”或一句也说不出的人数为( )
A.69 B.84
C.108 D.115
2.某医用口罩生产厂家生产A、B、C三种不同口罩,A、B、C三种口罩产量之比为2∶m∶1.为了调查这三种口罩的质量,用分层随机抽样的方法抽取一个容量为n的样本,样本中B种口罩数量比A种多40只,比C种多80只,则n=( )
A.240 B.280
C.320 D.360
易错点2 对频率分布直方图的特征理解有误致错
3.(多选题)某高中为了积极响应国家“阳光体育运动”的号召,调查该校3 000名学生每周平均体育运动时间的情况,从高一、高二、高三三个年级学生中按照4∶3∶3的比例进行分层随机抽样,收集了300名学生每周平均体育运动时间的数据(单位:小时),整理后得到如图所示的频率分布直方图.下列说法正确的是( )
A.估计该校学生每周平均体育运动时间为5.8小时
B.估计高一年级学生每周平均体育运动时间不足4小时的人数为300
C.估计该校学生每周平均体育运动时间不少于8小时的百分比为10%
D.估计该校学生每周平均体育运动时间不少于8小时的人数为600
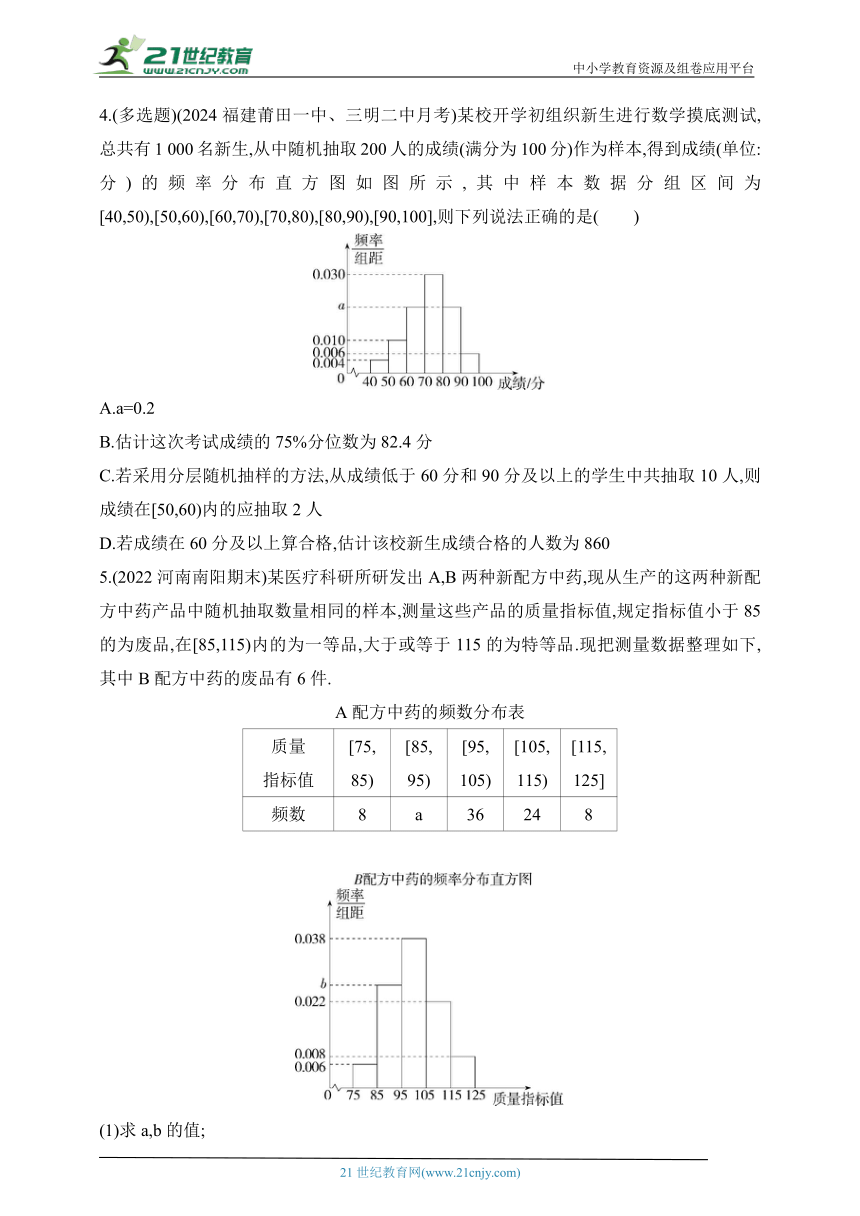
4.(多选题)(2024福建莆田一中、三明二中月考)某校开学初组织新生进行数学摸底测试,总共有1 000名新生,从中随机抽取200人的成绩(满分为100分)作为样本,得到成绩(单位:分)的频率分布直方图如图所示,其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则下列说法正确的是( )
A.a=0.2
B.估计这次考试成绩的75%分位数为82.4分
C.若采用分层随机抽样的方法,从成绩低于60分和90分及以上的学生中共抽取10人,则成绩在[50,60)内的应抽取2人
D.若成绩在60分及以上算合格,估计该校新生成绩合格的人数为860
5.(2022河南南阳期末)某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
思想方法练
一、数形结合思想
1.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系是( )
A.s1>s2>s3 B.s1>s3>s2 C.s3>s2>s1 D.s3>s1>s2
2.(2023上海长宁一模)甲、乙两城市某月初连续7天的日均气温数据如图所示:
则在这7天中:
①甲城市日均气温的中位数与平均数相等;
②甲城市的日均气温比乙城市的日均气温稳定;
③乙城市日均气温的极差为3 ℃;
④乙城市日均气温的众数为5 ℃.
以上判断正确的是 .(写出所有正确判断的序号)
3.(2024湖北宜昌第一高级中学月考)某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x(单位:t),月用水量不超过x的部分按平价收费,超出的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样获得100位居民某年的月平均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值;
(2)已知该市有80万居民,请估计全市居民中月平均用水量不低于3 t的人数;
(3)若该市政府希望使85%的居民每月的用水量不超过x t,估计x的值,并说明理由.
二、函数与方程思想
4.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升,现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
5.设样本数据x1,x2,…,x2 021的平均数为,方差为s2,若新数据2x1+1,2x2+1,…,2x2 021+1的平均数比方差大3,则s2- 2的最大值为 .
答案与分层梯度式解析
本章复习提升
易混易错练
1.D 由题意,得100名学生中只能说出第一句“春”或一句也说不出的学生有100-45-32=23(人),
故估计该校三年级的500名学生中,对“二十四节气歌”只能说出第一句“春”或一句也说不出的有500×=115(人).
2.A 设样本中A、B、C三种口罩分别有a只,b只,c只,
则即=2,∴b=120,
则a=80,c=40,故n=a+b+c=240.
故选A.
易错警示 分层随机抽样就是按比例抽样,因此列比例式时要注意“=”两边的标准是否一致.
3.ABD 对于A,估计该校学生每周平均体育运动时间为1×0.05+3×0.2+5×0.3+7×0.25+9×0.15+11×0.05=5.8(小时),故选项A正确;
对于B,高一年级的总人数为3 000×=1 200,由题中频率分布直方图可知,该校学生每周平均体育运动时间不足4小时的频率为(0.025+0.1)×2=0.25,所以估计高一年级学生每周平均体育运动时间不足4小时的人数为1 200×0.25=300,故选项B正确;
对于C,该校学生每周平均体育运动时间不少于8小时的百分比为(0.075+0.025)×2×100%=20%,故选项C错误;
对于D,该校学生每周平均体育运动时间不少于8小时的人数为3 000×20%=600,故选项D正确.
故选ABD.
4.BD 对于A,由(0.004+0.010+2a+0.030+0.006)×10=1得a=0.025,故A错误;
对于B,成绩在[40,80)内的频率为(0.004+0.010+0.025+0.030)×10=0.69,
成绩在[40,90)内所占的频率为(0.004+0.010+0.025×2+0.030)×10=0.94,
故75%分位数所在区间为[80,90),设75%分位数为x分,
则0.69+(x-80)×0.025=0.75,解得x=82.4,故B正确;
对于C,低于60分和90分及以上的学生所占的频率为(0.004+0.010+0.006)×10=0.2,
成绩在[50,60)内的频率为0.010×10=0.1,
故成绩在[50,60)内的应抽取×10=5(人),故C错误;
对于D,估计该校新生成绩在60分以下的人数为1 000×(0.004+0.010)×10=140,
故估计该校新生成绩合格的人数为1 000-140=860,故D正确.
故选BD.
易错警示 利用频率分布直方图解决相关问题时要注意三点:一是纵轴表示频率与组距的比值;二是频率分布直方图中小矩形的面积是频率;三是频率分布直方图中原始数据损失,各组数据往往用每组区间的中点值代替.
5.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,
所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,解得b=0.026.
(2)A配方中药的质量指标值的平均数×(80×8+90×24+100×36+110×24+120×8)=100,
方差×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,,即两种配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
对应主书P120
1.A 观察题中三个频率分布直方图,可得
甲的数据绝大部分都处在两端,数据大多离平均数远,表现得最分散,所以其标准差最大;
乙的数据分布均匀,数据偏离平均数的程度比甲低,故其标准差比甲的标准差小;
丙的数据绝大部分都在平均数左右,数据最集中,所以其标准差最小.
所以s1>s2>s3,故选A.
2.答案 ①④
解析 甲城市7天的日均气温分别为5 ℃,3 ℃,6 ℃,3 ℃,7 ℃,5 ℃,6 ℃;
乙城市7天的日均气温分别为5 ℃,4 ℃,6 ℃,5 ℃,5 ℃,4 ℃,6 ℃.
由折线图读出原始数据,进而利用相关公式得出中位数、平均数、众数、极差等,体现了数形结合思想.
对于①,甲城市日均气温的中位数为5 ℃,平均数为=5(℃),故①正确;
由折线图可直观看出两城市日均气温的变化趋势.
对于②,根据折线图知乙城市的日均气温更稳定,故②错误;
对于③,乙城市日均气温的极差为2 ℃,故③错误;
对于④,乙城市日均气温的众数为5 ℃,故④正确.
3.解析 根据频率分布直方图中的信息解决相关问题.
(1)由频率分布直方图中小矩形的面积之和等于1,可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
(2)100位居民中月平均用水量不低于3 t的频率为
(0.12+0.08+0.04)×0.5=0.12,
由此可估计全市80万居民中月平均用水量不低于3 t的人数为800 000×0.12=96 000.
(3)由题意知,只需求样本数据的85%分位数,即85%分位数为x t,
因为前6组频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)×0.5=0.88>0.85,
前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,
所以2.5≤x<3,
由0.3×(x-2.5)=0.85-0.73,解得x=2.9,
因此,估计月用水量标准为2.9 t时,85%的居民每月的用水量不超过标准.
方法点津 数形结合思想是统计学中很重要的一种思想方法.一方面用图形可以直观表示相关统计量;另一方面可以借助图形分析样本数据的分布状况、变化趋势、变量间的关系等,进而估计总体的状况.常见的图形有条形统计图、扇形统计图、折线统计图、频率分布直方图等,要熟练掌握它们的特点.
4.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1,列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义,列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
5.答案 -1
解析 设数据2x1+1,2x2+1,…,2x2 021+1的平均数为,方差为,则=4s2.
因为新数据的平均数比方差大3,
所以2+1=4s2+3,可得s2=,
列出s2- 2的表达式,利用二次函数的性质求最值,充分体现了函数思想.
则s2- 2=.
由s2=≥0,可得≥1,
由二次函数的性质知,当=1时,s2-取得最大值,且最大值为-1.
思想方法 在统计问题中常通过频率分布直方图的相关性质和样本数字特征的相关公式列方程解决问题,在求数字特征时,偶尔也会通过构造函数,结合函数的性质求最值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第一册
本章复习提升
易混易错练
易错点1 对分层随机抽样的抽样比理解不准确致错
1.中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气歌”是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气歌”,只能说出春、夏两句的有45人,能说出春、夏、秋三句及以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气歌”只能说出第一句“春”或一句也说不出的人数为( )
A.69 B.84
C.108 D.115
2.某医用口罩生产厂家生产A、B、C三种不同口罩,A、B、C三种口罩产量之比为2∶m∶1.为了调查这三种口罩的质量,用分层随机抽样的方法抽取一个容量为n的样本,样本中B种口罩数量比A种多40只,比C种多80只,则n=( )
A.240 B.280
C.320 D.360
易错点2 对频率分布直方图的特征理解有误致错
3.(多选题)某高中为了积极响应国家“阳光体育运动”的号召,调查该校3 000名学生每周平均体育运动时间的情况,从高一、高二、高三三个年级学生中按照4∶3∶3的比例进行分层随机抽样,收集了300名学生每周平均体育运动时间的数据(单位:小时),整理后得到如图所示的频率分布直方图.下列说法正确的是( )
A.估计该校学生每周平均体育运动时间为5.8小时
B.估计高一年级学生每周平均体育运动时间不足4小时的人数为300
C.估计该校学生每周平均体育运动时间不少于8小时的百分比为10%
D.估计该校学生每周平均体育运动时间不少于8小时的人数为600
4.(多选题)(2024福建莆田一中、三明二中月考)某校开学初组织新生进行数学摸底测试,总共有1 000名新生,从中随机抽取200人的成绩(满分为100分)作为样本,得到成绩(单位:分)的频率分布直方图如图所示,其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],则下列说法正确的是( )
A.a=0.2
B.估计这次考试成绩的75%分位数为82.4分
C.若采用分层随机抽样的方法,从成绩低于60分和90分及以上的学生中共抽取10人,则成绩在[50,60)内的应抽取2人
D.若成绩在60分及以上算合格,估计该校新生成绩合格的人数为860
5.(2022河南南阳期末)某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
思想方法练
一、数形结合思想
1.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系是( )
A.s1>s2>s3 B.s1>s3>s2 C.s3>s2>s1 D.s3>s1>s2
2.(2023上海长宁一模)甲、乙两城市某月初连续7天的日均气温数据如图所示:
则在这7天中:
①甲城市日均气温的中位数与平均数相等;
②甲城市的日均气温比乙城市的日均气温稳定;
③乙城市日均气温的极差为3 ℃;
④乙城市日均气温的众数为5 ℃.
以上判断正确的是 .(写出所有正确判断的序号)
3.(2024湖北宜昌第一高级中学月考)某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x(单位:t),月用水量不超过x的部分按平价收费,超出的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样获得100位居民某年的月平均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中a的值;
(2)已知该市有80万居民,请估计全市居民中月平均用水量不低于3 t的人数;
(3)若该市政府希望使85%的居民每月的用水量不超过x t,估计x的值,并说明理由.
二、函数与方程思想
4.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升,现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
5.设样本数据x1,x2,…,x2 021的平均数为,方差为s2,若新数据2x1+1,2x2+1,…,2x2 021+1的平均数比方差大3,则s2- 2的最大值为 .
答案与分层梯度式解析
本章复习提升
易混易错练
1.D 由题意,得100名学生中只能说出第一句“春”或一句也说不出的学生有100-45-32=23(人),
故估计该校三年级的500名学生中,对“二十四节气歌”只能说出第一句“春”或一句也说不出的有500×=115(人).
2.A 设样本中A、B、C三种口罩分别有a只,b只,c只,
则即=2,∴b=120,
则a=80,c=40,故n=a+b+c=240.
故选A.
易错警示 分层随机抽样就是按比例抽样,因此列比例式时要注意“=”两边的标准是否一致.
3.ABD 对于A,估计该校学生每周平均体育运动时间为1×0.05+3×0.2+5×0.3+7×0.25+9×0.15+11×0.05=5.8(小时),故选项A正确;
对于B,高一年级的总人数为3 000×=1 200,由题中频率分布直方图可知,该校学生每周平均体育运动时间不足4小时的频率为(0.025+0.1)×2=0.25,所以估计高一年级学生每周平均体育运动时间不足4小时的人数为1 200×0.25=300,故选项B正确;
对于C,该校学生每周平均体育运动时间不少于8小时的百分比为(0.075+0.025)×2×100%=20%,故选项C错误;
对于D,该校学生每周平均体育运动时间不少于8小时的人数为3 000×20%=600,故选项D正确.
故选ABD.
4.BD 对于A,由(0.004+0.010+2a+0.030+0.006)×10=1得a=0.025,故A错误;
对于B,成绩在[40,80)内的频率为(0.004+0.010+0.025+0.030)×10=0.69,
成绩在[40,90)内所占的频率为(0.004+0.010+0.025×2+0.030)×10=0.94,
故75%分位数所在区间为[80,90),设75%分位数为x分,
则0.69+(x-80)×0.025=0.75,解得x=82.4,故B正确;
对于C,低于60分和90分及以上的学生所占的频率为(0.004+0.010+0.006)×10=0.2,
成绩在[50,60)内的频率为0.010×10=0.1,
故成绩在[50,60)内的应抽取×10=5(人),故C错误;
对于D,估计该校新生成绩在60分以下的人数为1 000×(0.004+0.010)×10=140,
故估计该校新生成绩合格的人数为1 000-140=860,故D正确.
故选BD.
易错警示 利用频率分布直方图解决相关问题时要注意三点:一是纵轴表示频率与组距的比值;二是频率分布直方图中小矩形的面积是频率;三是频率分布直方图中原始数据损失,各组数据往往用每组区间的中点值代替.
5.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,
所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,解得b=0.026.
(2)A配方中药的质量指标值的平均数×(80×8+90×24+100×36+110×24+120×8)=100,
方差×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,,即两种配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
对应主书P120
1.A 观察题中三个频率分布直方图,可得
甲的数据绝大部分都处在两端,数据大多离平均数远,表现得最分散,所以其标准差最大;
乙的数据分布均匀,数据偏离平均数的程度比甲低,故其标准差比甲的标准差小;
丙的数据绝大部分都在平均数左右,数据最集中,所以其标准差最小.
所以s1>s2>s3,故选A.
2.答案 ①④
解析 甲城市7天的日均气温分别为5 ℃,3 ℃,6 ℃,3 ℃,7 ℃,5 ℃,6 ℃;
乙城市7天的日均气温分别为5 ℃,4 ℃,6 ℃,5 ℃,5 ℃,4 ℃,6 ℃.
由折线图读出原始数据,进而利用相关公式得出中位数、平均数、众数、极差等,体现了数形结合思想.
对于①,甲城市日均气温的中位数为5 ℃,平均数为=5(℃),故①正确;
由折线图可直观看出两城市日均气温的变化趋势.
对于②,根据折线图知乙城市的日均气温更稳定,故②错误;
对于③,乙城市日均气温的极差为2 ℃,故③错误;
对于④,乙城市日均气温的众数为5 ℃,故④正确.
3.解析 根据频率分布直方图中的信息解决相关问题.
(1)由频率分布直方图中小矩形的面积之和等于1,可得(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
(2)100位居民中月平均用水量不低于3 t的频率为
(0.12+0.08+0.04)×0.5=0.12,
由此可估计全市80万居民中月平均用水量不低于3 t的人数为800 000×0.12=96 000.
(3)由题意知,只需求样本数据的85%分位数,即85%分位数为x t,
因为前6组频率之和为(0.08+0.16+0.30+0.40+0.52+0.30)×0.5=0.88>0.85,
前5组的频率之和为(0.08+0.16+0.30+0.40+0.52)×0.5=0.73<0.85,
所以2.5≤x<3,
由0.3×(x-2.5)=0.85-0.73,解得x=2.9,
因此,估计月用水量标准为2.9 t时,85%的居民每月的用水量不超过标准.
方法点津 数形结合思想是统计学中很重要的一种思想方法.一方面用图形可以直观表示相关统计量;另一方面可以借助图形分析样本数据的分布状况、变化趋势、变量间的关系等,进而估计总体的状况.常见的图形有条形统计图、扇形统计图、折线统计图、频率分布直方图等,要熟练掌握它们的特点.
4.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1,列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义,列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
5.答案 -1
解析 设数据2x1+1,2x2+1,…,2x2 021+1的平均数为,方差为,则=4s2.
因为新数据的平均数比方差大3,
所以2+1=4s2+3,可得s2=,
列出s2- 2的表达式,利用二次函数的性质求最值,充分体现了函数思想.
则s2- 2=.
由s2=≥0,可得≥1,
由二次函数的性质知,当=1时,s2-取得最大值,且最大值为-1.
思想方法 在统计问题中常通过频率分布直方图的相关性质和样本数字特征的相关公式列方程解决问题,在求数字特征时,偶尔也会通过构造函数,结合函数的性质求最值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
