2025北师大版高中数学必修第一册同步练习题--全书综合测评(含解析)
文档属性
| 名称 | 2025北师大版高中数学必修第一册同步练习题--全书综合测评(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 421.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 21:38:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第一册
全书综合测评
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|0A.(3,16) B.(3,8) C.(1,3] D.(1,+∞)
2.已知函数f(x)=(m2-m-1)是幂函数,且为偶函数,则实数m=( )
A.2或-1` B.-1
C.4` D.2
3.函数f(x)=的大致图象是( )
A B C D
4.已知甲、乙两名运动员进行射击比赛,每名运动员射击10次,得分情况如图表所示,则根据本次比赛结果,以下说法正确的是( )
乙射击环数 6 7 8 9 10
频数 1 2 2 2 3
A.通过判断甲、乙射击成绩的平均数知甲比乙的射击水平更高
B.甲的射击水平更稳定
C.甲射击成绩的中位数大于乙射击成绩的中位数
D.甲射击成绩的众数大于乙射击成绩的众数
5.已知函数f(x)=log2·log2,若f(x1)=f(x2)(其中x1≠x2),则的最小值为( )
A. C.2 D.4
6.一组数据x1,x2,…,xn(n∈N+)的平均数为,方差为s2,则下列说法正确的是( )
A.若s2=0,则xi(i=1,2,…,n)都为0
B.若=3,则另一组数据yi=2xi+1(i=1,2,…,n)的平均数为6
C.若s2=3,则另一组数据yi=2xi+1(i=1,2,…,n)的方差为12
D.若数据x1,x2,…,xn的25%分位数为90,则可以估计总体中至少有75%的数据不大于90
7.已知函数f(x)=若f(x)恰有3个零点x1,x2,x3,则x1x2x3的取值范围是( )
A.
8.已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y), f =1,如果对于任意y>x>0,都有f(x)>f(y),那么不等式f(-x)+f(3-x)≥-2的解集为( )
A.[-4,0) B.[-1,0)` C.(-∞,0] D.[-1,4]
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.若3a+log7a=3b+log7(7b),则( )
A.ab D.a>7b
10.算盘是我国古代一项伟大的发明,是一种重要的计算工具.一把算盘的初始状态如图所示,自右向左,各档分别表示个位、十位、百位、千位……,梁上面每一粒珠子(简称上珠)代表5,梁下面每一粒珠子(简称下珠)代表1,即五粒下珠的大小等于同组一粒上珠的大小.例如,个位拨动一粒上珠靠梁且十位拨动一粒下珠靠梁,表示的数为15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子靠梁,设事件A=“表示的四位数能被3整除”,B=“表示的四位数能被5整除”,则( )
A.P(A)=
C.P(A∪B)=
11.已知函数f(x)=方程[f(x)]2-mf(x)-1=0有4个不同的实数根,则下列选项正确的是( )
A.函数f(x)的零点的个数为2
B.实数m的取值范围为
C.函数f(x)无最值
D.函数f(x)在(0,+∞)上单调递增
三、填空题(本题共3小题,每小题5分,共15分)
12.为了解中学生对“双减”政策落实的满意度,某部门欲从A,B两校共4 000名中学生中,用分层随机抽样的方法抽取240名中学生进行问卷调查,已知A校有1 800名中学生,则应在B校抽取的中学生人数是 .
13.已知函数f(x),g(x)分别为定义在R上的奇函数和偶函数,且满足f(x)+g(x)=2x+1.若函数h(x)=4x+2-x-g(x),x∈[-2,1],则h(x)的值域为 .
14.在实数集R中定义一种具有下列性质的运算“*”:
(1)对任意a,b∈R,a*b=b*a;
(2)对任意a∈R,a*0=a;
(3)对任意a,b,c∈R,(a*b)*c=c*(ab)+(a*c)+(b*c)-5c.
则函数f(x)=x*(x>0)的最小值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知全集为R,集合A={x|x2<4},B={x|(x-m-1)(x-m-7)>0}.
(1)若m=-2,求集合A∪ RB;
(2)请在①“x∈A”是“x∈B”的充分不必要条件;②若x∈A,则x B;③A RB这三个条件中任选一个,补充在下面问题的横线上,并解答.
若 ,求实数m的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
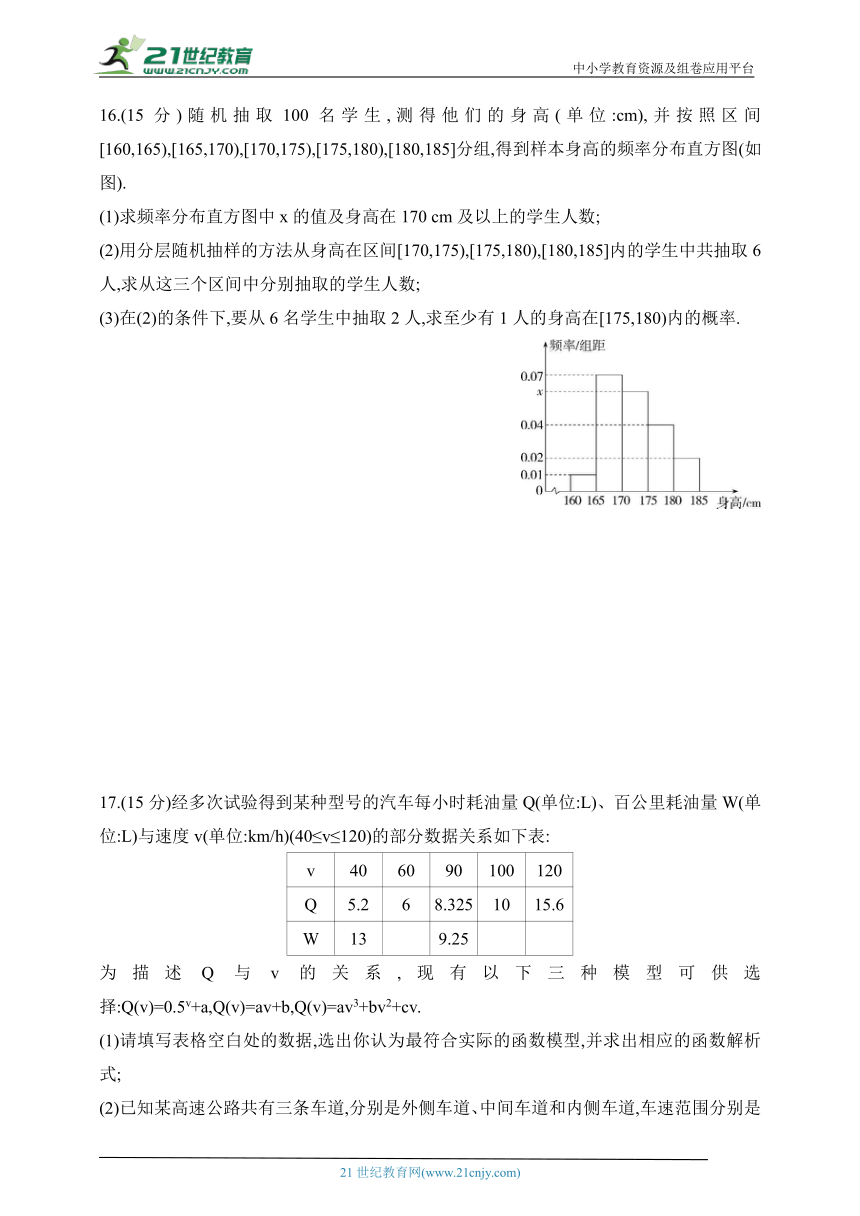
16.(15分)随机抽取100名学生,测得他们的身高(单位:cm),并按照区间[160,165),[165,170),[170,175),[175,180),[180,185]分组,得到样本身高的频率分布直方图(如图).
(1)求频率分布直方图中x的值及身高在170 cm及以上的学生人数;
(2)用分层随机抽样的方法从身高在区间[170,175),[175,180),[180,185]内的学生中共抽取6人,求从这三个区间中分别抽取的学生人数;
(3)在(2)的条件下,要从6名学生中抽取2人,求至少有1人的身高在[175,180)内的概率.
17.(15分)经多次试验得到某种型号的汽车每小时耗油量Q(单位:L)、百公里耗油量W(单位:L)与速度v(单位:km/h)(40≤v≤120)的部分数据关系如下表:
v 40 60 90 100 120
Q 5.2 6 8.325 10 15.6
W 13 9.25
为描述Q与v的关系,现有以下三种模型可供选择:Q(v)=0.5v+a,Q(v)=av+b,Q(v)=av3+bv2+cv.
(1)请填写表格空白处的数据,选出你认为最符合实际的函数模型,并求出相应的函数解析式;
(2)已知某高速公路共有三条车道,分别是外侧车道、中间车道和内侧车道,车速范围分别是[60,90),[90,110),[110,120](单位:km/h),则该型号汽车在哪条车道以什么速度行驶时百公里耗油量最小
18.(17分)已知函数f(x)=x2,对任意实数t,gt(x)=-tx+1.
(1)若函数h(x)=-gt(x)在(0,2]上是单调递减的,求实数t的取值范围;
(2)若f(x)19.(17分)已知函数f(x)=log3x.
(1)设函数g(x)是定义在R上的奇函数,当x>0时,g(x)=f(x),求函数g(x)的解析式;
(2)已知集合A={x|3(log3x)2-20log9x+3≤0}.
①求集合A;
②当x∈A时,函数h(x)=f·f的最小值为-2,求实数a的值.
答案与解析
全书综合测评
1.A 集合A={x|02.D 由幂函数的定义知m2-m-1=1,解得m=-1或m=2.
因为f(x)为偶函数,所以m2-2m-2为偶数,故m=2.故选D.
3.A 由ex-e-x≠0,得x≠0,所以f(x)的定义域是{x|x≠0},关于原点对称,
f(-x)==f(x),所以f(x)是偶函数,图象关于y轴对称,排除D;
当x>0时,ex>e-x,所以f(x)>0,由f(x)是偶函数可知,f(x)>0在(-∞,0)∪(0,+∞)上恒成立,排除C;
当x趋近于+∞时,ex趋近于+∞,e-x趋近于0,且指数增长快得多,所以f(x)趋近于0,排除B.
4.B 甲射击成绩的平均数×(5+7+3×8+4×9+10)=8.2,
乙射击成绩的平均数×(6+2×7+2×8+2×9+3×10)=8.4,
∵,∴乙的射击水平更高,故A错误;
甲射击成绩的方差×[(5-8.2)2+(7-8.2)2+3×(8-8.2)2+4×(9-8.2)2+(10-8.2)2]=1.76,
乙射击成绩的方差×[(6-8.4)2+2×(7-8.4)2+2×(8-8.4)2+2×(9-8.4)2+3×(10-8.4)2]=1.84,
∵,∴甲的射击水平更稳定,故B正确;
甲的射击成绩由小到大排列为5,7,8,8,8,9,9,9,9,10,位于第5、6位的数分别是8,9,所以甲射击成绩的中位数是=8.5,
乙的射击成绩由小到大排列为6,7,7,8,8,9,9,10,10,10,位于第5、6位的数分别是8,9,所以乙射击成绩的中位数是=8.5,故C错误;
甲射击成绩的众数为9,乙射击成绩的众数为10,故D错误.
故选B.
5.B f(x)=log2·log2=(log2x-1)(log2x-3)=(log2x)2-4log2x+3.
因为f(x1)=f(x2)(其中x1≠x2),
所以log2x1+log2x2=4,即x1x2=16,
所以≥2,当且仅当且x1x2=16,即x1=,x2=12时取“=”.故选B.
6.C 对于A,数据x1,x2,…,xn的方差s2=0时,说明所有的数据x1,x2,…,xn都相等,但不一定为0,故A错误;
对于B,数据x1,x2,…,xn的平均数=3,则数据yi=2xi+1(i=1,2,…,n)的平均数为2×3+1=7,故B错误;
对于C,数据x1,x2,…,xn的方差s2=3,则数据yi=2xi+1(i=1,2,…,n)的方差为22×3=12,故C正确;
对于D,数据x1,x2,…,xn的25%分位数为90,则可以估计总体中至少有75%的数据大于或等于90,故D错误.
故选C.
7.A 设g(x)=
则f(x)恰有3个零点x1,x2,x3,即g(x)=的图象与直线y=-m恰有3个不同的交点,
g(x)=的图象和直线y=-m如图所示.
不妨设x1所以-lg x2=lg x3,即lg x2+lg x3=0,所以x2x3=1,
所以x1x2x3=x1∈,
故选A.
8.B 令x=y=1,得f(1)=2f(1),即f(1)=0;令x=,y=2,得f(1)=f(2)+f ,即f(2)=-1;令x=y=2,得f(4)=2f(2)=-2.由f(-x)+f(3-x)≥-2,可得f(x2-3x)≥f(4),又因为函数f(x)的定义域是(0,+∞),且对于任意0f(y),所以解得-1≤x<0,即不等式f(-x)+f(3-x)≥-2的解集为[-1,0).
9.BC 由题意得a>0,b>0,所以7b>b,
设函数f(x)=3x+log 7x,则f(x)是增函数,
由3a+log 7a=3b+log 7(7b)=3b+log 7b+1>3b+log 7b,得f(a)>f(b),所以a>b.
由3a+log 7a=3b+log 7(7b)<37b+log 7(7b),得f(a)故选BC.
10.ACD 将算盘的个位、十位、百位、千位分别随机拨动一粒珠子靠梁,所得四位数共16个,分别为1 111,1 115,1 151,1 155,1 511,1 515,1 551,1 555,5 111,5 115,5 151,5 155,5 511,5 515,5 551,5 555.
事件A包含的样本点有1 155,1 515,1 551,5 115,5 151,5 511,共6个,因此P(A)=;事件B包含的样本点有1 115,1 155,1 515,1 555,5 115,5 155,5 515,5 555,共8个,因此P(B)=;事件A∪B包含的样本点有1 115,1 155,1 515,1 551,1 555,5 115,5 151,5 155,5 511,5 515,5 555,共11个,因此P(A∪B)=;事件AB包含的样本点有1 155,1 515,5 115,共3个,因此P(AB)=.故选ACD.
11.ABC 作出f(x)的图象,如图所示,
由图可知, f(x)有x=-2和x=1两个零点,无最值,且在(0,+∞)上不单调,故A,C正确,D错误.令t=f(x),由方程[f(x)]2-mf(x)-1=0有4个不同的实数根,得方程t2-mt-1=0有2个实数根,设这两根分别为t1,t2,t1结合图象可知t1<0,0所以f(x)≤-或0由[f(x)]2-mf(x)-1=0,得m=f(x)-,
易知函数y=x-和(0,2]上单调递增,
当f(x)=-时,m=,当f(x)=2时,m=,
所以m≤,故B正确.故选ABC.
12.答案 132
解析 ∵A,B两校共4 000名中学生,且A校有1 800名中学生,∴B校有2 200名中学生,从A,B两校中用分层随机抽样的方法抽取240名中学生,每个学生被抽到的概率为,∴应在B校抽取的中学生人数是2 200×=132.
13.答案
解析 由f(x)+g(x)=2x+1得f(-x)+g(-x)=2-x+1,
因为函数f(x),g(x)分别为定义在R上的奇函数和偶函数,
所以-f(x)+g(x)=2-x+1,所以g(x)=2x+2-x,
所以h(x)=-2x,
令t=2x,x∈[-2,1],则t∈,
所以(2x)2-2x=t2-t=,
所以h(x)的值域为.
14.答案 3
解析 在(a*b)*c=c*(ab)+(a*c)+(b*c)-5c中,令c=0,得(a*b)*0=0*(ab)+(a*0)+(b*0),由性质(1)a*b=b*a,可得(a*b)*0=(ab)*0+(a*0)+(b*0),由性质(2)a*0=a,可得(a*b)*0=a*b,(ab)*0+(a*0)+(b*0)=ab+a+b,所以a*b=ab+a+b,所以f(x)=x*.因为x>0,所以f(x)=1+x+≥3,当且仅当x=,即x=1时,等号成立,所以f(x)的最小值为3.
15.解析 (1)A={x|x2<4}=(-2,2),(1分)
当m=-2时,B={x|(x+1)(x-5)>0}=(-∞,-1)∪(5,+∞),(2分)
∴ RB=[-1,5],(4分)
∴A∪ RB=(-2,5].(6分)
(2)易得A=(-2,2),B={x|(x-m-1)(x-m-7)>0}=(-∞,m+1)∪(m+7,+∞).(8分)
若选①,则A B,(10分)
所以m+1≥2或m+7≤-2,解得m≥1或m≤-9,(12分)
所以实数m的取值范围为(-∞,-9]∪[1,+∞).(13分)
若选②,则A∩B= ,(10分)
所以m+1≤-2且m+7≥2,解得-5≤m≤-3,(12分)
所以实数m的取值范围为[-5,-3].(13分)
若选③,易得 RB=[m+1,m+7],(10分)
则m+1≤-2且m+7≥2,解得-5≤m≤-3,(12分)
所以实数m的取值范围为[-5,-3].(13分)
16.解析 (1)由频率分布直方图可知,5x=1-5×(0.07+0.04+0.02+0.01),
所以x=0.06.(2分)
因此身高在170 cm及以上的学生人数为100×(0.06×5+0.04×5+0.02×5)=60.(4分)
(2)身高在[170,175),[175,180),[180,185]内的学生人数分别为0.06×5×100=30,0.04×5×100=20,0.02×5×100=10,(6分)
因此应该从身高在[170,175),[175,180),[180,185]内的学生中分别抽取6×=3(人),6×=2(人),6×=1(人).(8分)
(3)在(2)的条件下,设身高在[170,175)内的3名学生分别为A1,A2,A3,身高在[175,180)内的2名学生分别为B1,B2,身高在[180,185]内的1名学生为C0,则从6名学生中抽取2人的样本点共15个,分别为(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C0),(A2,A3),(A2,B1),(A2,B2),(A2,C0),(A3,B1),(A3,B2),(A3,C0),(B1,B2),(B1,C0),(B2,C0),(11分)
至少有1人的身高在[175,180)内包含的样本点有9个,分别为(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C0),(B2,C0),(13分)
所以至少有1人的身高在[175,180)内的概率为.(15分)
17.解析 (1)填表如下:
v 40 60 90 100 120
Q 5.2 6 8.325 10 15.6
W 13 10 9.25 10 13
(3分)
由题意可得符合的函数模型需满足在40≤v≤120时有意义,且在[40,120]上单调递增.
Q(v)=0.5v+a在[40,120]上单调递减,不符合题意.(5分)
若选择Q(v)=av+b,代入(40,5.2),(60,6),
得
则Q(v)=0.04v+3.6,此时Q(90)=7.2,Q(100)=7.6,Q(120)=8.4,
与实际数据相差较大,所以不符合题意.(7分)
经观察,函数模型Q(v)=av3+bv2+cv最符合实际,(9分)
代入(40,5.2),(60,6),(100,10),
则
∴Q(v)=0.000 025v3-0.004v2+0.25v.(11分)
(2)∵W=×Q=0.002 5v2-0.4v+25=0.002 5(v-80)2+9,
∴当v=80时,W取得最小值9,(13分)
故该型号汽车在外侧车道以80 km/h的速度行驶时百公里耗油量最小. (15分)
18.解析 (1)由已知得h(x)=+tx-1,(2分)
任取x1,x2∈(0,2],且x1则h(x1)-h(x2)=,
要使h(x)在(0,2]上单调递减,只需h(x1)-h(x2)>0恒成立. (4分)
∵x2-x1>0,0∴只需1-tx1x2>0,即t<,x1,x2∈(0,2]恒成立.(6分)
又∵,∴t≤,∴实数t的取值范围是.(8分)
(2)解法一:由f(x)∵x∈,∴00,∴.(11分)
∵f(x)∴当x∈时,.(13分)
∵-1,
∴当x=时,函数y=取得最小值3,∴<3.(15分)
又m>0,∴m>,∴正数m的取值范围是.(17分)
解法二:由f(x)令F(x)=x2+2mx-m,则F(x)<0对任意x∈恒成立,(12分)
∴解得m>.(15分)
∴正数m的取值范围是.(17分)
19.解析 (1)由题意得,当x>0时,g(x)=log3x.
因为g(x)为R上的奇函数,所以g(0)=0,g(x)=-g(-x).
当x<0时,-x>0,所以g(x)=-g(-x)=-log3(-x).
综上,g(x)=(4分)
(2)①不等式3(log3x)2-20log9x+3≤0可化为3(log3x)2-10log3x+3≤0,
即(3log3x-1)(log3x-3)≤0,所以≤log3x≤3,解得≤x≤27,
所以集合A=[,27].(7分)
②h(x)=f·f·log3
=(log3x-a)(log3x-2)=(log3x)2-(a+2)log3x+2a.(9分)
设t=log3x,则t∈.(11分)
当,即a≤-时,函数s(t)在上单调递增,
所以s(t)min=s=-2,解得a=-(舍去);(13分)
当≥3,即a≥4时,函数s(t)在上单调递减,
所以s(t)min=s(3)=3-a=-2,解得a=5;(15分)
当<3,即-所以s(t)min=s=-2,
解得a=2-2或a=2+2(舍去).
综上,实数a的值为2-2或5.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第一册
全书综合测评
全卷满分150分 考试用时120分钟
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合A={x|0
2.已知函数f(x)=(m2-m-1)是幂函数,且为偶函数,则实数m=( )
A.2或-1` B.-1
C.4` D.2
3.函数f(x)=的大致图象是( )
A B C D
4.已知甲、乙两名运动员进行射击比赛,每名运动员射击10次,得分情况如图表所示,则根据本次比赛结果,以下说法正确的是( )
乙射击环数 6 7 8 9 10
频数 1 2 2 2 3
A.通过判断甲、乙射击成绩的平均数知甲比乙的射击水平更高
B.甲的射击水平更稳定
C.甲射击成绩的中位数大于乙射击成绩的中位数
D.甲射击成绩的众数大于乙射击成绩的众数
5.已知函数f(x)=log2·log2,若f(x1)=f(x2)(其中x1≠x2),则的最小值为( )
A. C.2 D.4
6.一组数据x1,x2,…,xn(n∈N+)的平均数为,方差为s2,则下列说法正确的是( )
A.若s2=0,则xi(i=1,2,…,n)都为0
B.若=3,则另一组数据yi=2xi+1(i=1,2,…,n)的平均数为6
C.若s2=3,则另一组数据yi=2xi+1(i=1,2,…,n)的方差为12
D.若数据x1,x2,…,xn的25%分位数为90,则可以估计总体中至少有75%的数据不大于90
7.已知函数f(x)=若f(x)恰有3个零点x1,x2,x3,则x1x2x3的取值范围是( )
A.
8.已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y), f =1,如果对于任意y>x>0,都有f(x)>f(y),那么不等式f(-x)+f(3-x)≥-2的解集为( )
A.[-4,0) B.[-1,0)` C.(-∞,0] D.[-1,4]
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.若3a+log7a=3b+log7(7b),则( )
A.a
10.算盘是我国古代一项伟大的发明,是一种重要的计算工具.一把算盘的初始状态如图所示,自右向左,各档分别表示个位、十位、百位、千位……,梁上面每一粒珠子(简称上珠)代表5,梁下面每一粒珠子(简称下珠)代表1,即五粒下珠的大小等于同组一粒上珠的大小.例如,个位拨动一粒上珠靠梁且十位拨动一粒下珠靠梁,表示的数为15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子靠梁,设事件A=“表示的四位数能被3整除”,B=“表示的四位数能被5整除”,则( )
A.P(A)=
C.P(A∪B)=
11.已知函数f(x)=方程[f(x)]2-mf(x)-1=0有4个不同的实数根,则下列选项正确的是( )
A.函数f(x)的零点的个数为2
B.实数m的取值范围为
C.函数f(x)无最值
D.函数f(x)在(0,+∞)上单调递增
三、填空题(本题共3小题,每小题5分,共15分)
12.为了解中学生对“双减”政策落实的满意度,某部门欲从A,B两校共4 000名中学生中,用分层随机抽样的方法抽取240名中学生进行问卷调查,已知A校有1 800名中学生,则应在B校抽取的中学生人数是 .
13.已知函数f(x),g(x)分别为定义在R上的奇函数和偶函数,且满足f(x)+g(x)=2x+1.若函数h(x)=4x+2-x-g(x),x∈[-2,1],则h(x)的值域为 .
14.在实数集R中定义一种具有下列性质的运算“*”:
(1)对任意a,b∈R,a*b=b*a;
(2)对任意a∈R,a*0=a;
(3)对任意a,b,c∈R,(a*b)*c=c*(ab)+(a*c)+(b*c)-5c.
则函数f(x)=x*(x>0)的最小值为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知全集为R,集合A={x|x2<4},B={x|(x-m-1)(x-m-7)>0}.
(1)若m=-2,求集合A∪ RB;
(2)请在①“x∈A”是“x∈B”的充分不必要条件;②若x∈A,则x B;③A RB这三个条件中任选一个,补充在下面问题的横线上,并解答.
若 ,求实数m的取值范围.
注:如果选择多个条件分别解答,按第一个解答计分.
16.(15分)随机抽取100名学生,测得他们的身高(单位:cm),并按照区间[160,165),[165,170),[170,175),[175,180),[180,185]分组,得到样本身高的频率分布直方图(如图).
(1)求频率分布直方图中x的值及身高在170 cm及以上的学生人数;
(2)用分层随机抽样的方法从身高在区间[170,175),[175,180),[180,185]内的学生中共抽取6人,求从这三个区间中分别抽取的学生人数;
(3)在(2)的条件下,要从6名学生中抽取2人,求至少有1人的身高在[175,180)内的概率.
17.(15分)经多次试验得到某种型号的汽车每小时耗油量Q(单位:L)、百公里耗油量W(单位:L)与速度v(单位:km/h)(40≤v≤120)的部分数据关系如下表:
v 40 60 90 100 120
Q 5.2 6 8.325 10 15.6
W 13 9.25
为描述Q与v的关系,现有以下三种模型可供选择:Q(v)=0.5v+a,Q(v)=av+b,Q(v)=av3+bv2+cv.
(1)请填写表格空白处的数据,选出你认为最符合实际的函数模型,并求出相应的函数解析式;
(2)已知某高速公路共有三条车道,分别是外侧车道、中间车道和内侧车道,车速范围分别是[60,90),[90,110),[110,120](单位:km/h),则该型号汽车在哪条车道以什么速度行驶时百公里耗油量最小
18.(17分)已知函数f(x)=x2,对任意实数t,gt(x)=-tx+1.
(1)若函数h(x)=-gt(x)在(0,2]上是单调递减的,求实数t的取值范围;
(2)若f(x)
(1)设函数g(x)是定义在R上的奇函数,当x>0时,g(x)=f(x),求函数g(x)的解析式;
(2)已知集合A={x|3(log3x)2-20log9x+3≤0}.
①求集合A;
②当x∈A时,函数h(x)=f·f的最小值为-2,求实数a的值.
答案与解析
全书综合测评
1.A 集合A={x|0
因为f(x)为偶函数,所以m2-2m-2为偶数,故m=2.故选D.
3.A 由ex-e-x≠0,得x≠0,所以f(x)的定义域是{x|x≠0},关于原点对称,
f(-x)==f(x),所以f(x)是偶函数,图象关于y轴对称,排除D;
当x>0时,ex>e-x,所以f(x)>0,由f(x)是偶函数可知,f(x)>0在(-∞,0)∪(0,+∞)上恒成立,排除C;
当x趋近于+∞时,ex趋近于+∞,e-x趋近于0,且指数增长快得多,所以f(x)趋近于0,排除B.
4.B 甲射击成绩的平均数×(5+7+3×8+4×9+10)=8.2,
乙射击成绩的平均数×(6+2×7+2×8+2×9+3×10)=8.4,
∵,∴乙的射击水平更高,故A错误;
甲射击成绩的方差×[(5-8.2)2+(7-8.2)2+3×(8-8.2)2+4×(9-8.2)2+(10-8.2)2]=1.76,
乙射击成绩的方差×[(6-8.4)2+2×(7-8.4)2+2×(8-8.4)2+2×(9-8.4)2+3×(10-8.4)2]=1.84,
∵,∴甲的射击水平更稳定,故B正确;
甲的射击成绩由小到大排列为5,7,8,8,8,9,9,9,9,10,位于第5、6位的数分别是8,9,所以甲射击成绩的中位数是=8.5,
乙的射击成绩由小到大排列为6,7,7,8,8,9,9,10,10,10,位于第5、6位的数分别是8,9,所以乙射击成绩的中位数是=8.5,故C错误;
甲射击成绩的众数为9,乙射击成绩的众数为10,故D错误.
故选B.
5.B f(x)=log2·log2=(log2x-1)(log2x-3)=(log2x)2-4log2x+3.
因为f(x1)=f(x2)(其中x1≠x2),
所以log2x1+log2x2=4,即x1x2=16,
所以≥2,当且仅当且x1x2=16,即x1=,x2=12时取“=”.故选B.
6.C 对于A,数据x1,x2,…,xn的方差s2=0时,说明所有的数据x1,x2,…,xn都相等,但不一定为0,故A错误;
对于B,数据x1,x2,…,xn的平均数=3,则数据yi=2xi+1(i=1,2,…,n)的平均数为2×3+1=7,故B错误;
对于C,数据x1,x2,…,xn的方差s2=3,则数据yi=2xi+1(i=1,2,…,n)的方差为22×3=12,故C正确;
对于D,数据x1,x2,…,xn的25%分位数为90,则可以估计总体中至少有75%的数据大于或等于90,故D错误.
故选C.
7.A 设g(x)=
则f(x)恰有3个零点x1,x2,x3,即g(x)=的图象与直线y=-m恰有3个不同的交点,
g(x)=的图象和直线y=-m如图所示.
不妨设x1
所以x1x2x3=x1∈,
故选A.
8.B 令x=y=1,得f(1)=2f(1),即f(1)=0;令x=,y=2,得f(1)=f(2)+f ,即f(2)=-1;令x=y=2,得f(4)=2f(2)=-2.由f(-x)+f(3-x)≥-2,可得f(x2-3x)≥f(4),又因为函数f(x)的定义域是(0,+∞),且对于任意0
9.BC 由题意得a>0,b>0,所以7b>b,
设函数f(x)=3x+log 7x,则f(x)是增函数,
由3a+log 7a=3b+log 7(7b)=3b+log 7b+1>3b+log 7b,得f(a)>f(b),所以a>b.
由3a+log 7a=3b+log 7(7b)<37b+log 7(7b),得f(a)
10.ACD 将算盘的个位、十位、百位、千位分别随机拨动一粒珠子靠梁,所得四位数共16个,分别为1 111,1 115,1 151,1 155,1 511,1 515,1 551,1 555,5 111,5 115,5 151,5 155,5 511,5 515,5 551,5 555.
事件A包含的样本点有1 155,1 515,1 551,5 115,5 151,5 511,共6个,因此P(A)=;事件B包含的样本点有1 115,1 155,1 515,1 555,5 115,5 155,5 515,5 555,共8个,因此P(B)=;事件A∪B包含的样本点有1 115,1 155,1 515,1 551,1 555,5 115,5 151,5 155,5 511,5 515,5 555,共11个,因此P(A∪B)=;事件AB包含的样本点有1 155,1 515,5 115,共3个,因此P(AB)=.故选ACD.
11.ABC 作出f(x)的图象,如图所示,
由图可知, f(x)有x=-2和x=1两个零点,无最值,且在(0,+∞)上不单调,故A,C正确,D错误.令t=f(x),由方程[f(x)]2-mf(x)-1=0有4个不同的实数根,得方程t2-mt-1=0有2个实数根,设这两根分别为t1,t2,t1
易知函数y=x-和(0,2]上单调递增,
当f(x)=-时,m=,当f(x)=2时,m=,
所以m≤,故B正确.故选ABC.
12.答案 132
解析 ∵A,B两校共4 000名中学生,且A校有1 800名中学生,∴B校有2 200名中学生,从A,B两校中用分层随机抽样的方法抽取240名中学生,每个学生被抽到的概率为,∴应在B校抽取的中学生人数是2 200×=132.
13.答案
解析 由f(x)+g(x)=2x+1得f(-x)+g(-x)=2-x+1,
因为函数f(x),g(x)分别为定义在R上的奇函数和偶函数,
所以-f(x)+g(x)=2-x+1,所以g(x)=2x+2-x,
所以h(x)=-2x,
令t=2x,x∈[-2,1],则t∈,
所以(2x)2-2x=t2-t=,
所以h(x)的值域为.
14.答案 3
解析 在(a*b)*c=c*(ab)+(a*c)+(b*c)-5c中,令c=0,得(a*b)*0=0*(ab)+(a*0)+(b*0),由性质(1)a*b=b*a,可得(a*b)*0=(ab)*0+(a*0)+(b*0),由性质(2)a*0=a,可得(a*b)*0=a*b,(ab)*0+(a*0)+(b*0)=ab+a+b,所以a*b=ab+a+b,所以f(x)=x*.因为x>0,所以f(x)=1+x+≥3,当且仅当x=,即x=1时,等号成立,所以f(x)的最小值为3.
15.解析 (1)A={x|x2<4}=(-2,2),(1分)
当m=-2时,B={x|(x+1)(x-5)>0}=(-∞,-1)∪(5,+∞),(2分)
∴ RB=[-1,5],(4分)
∴A∪ RB=(-2,5].(6分)
(2)易得A=(-2,2),B={x|(x-m-1)(x-m-7)>0}=(-∞,m+1)∪(m+7,+∞).(8分)
若选①,则A B,(10分)
所以m+1≥2或m+7≤-2,解得m≥1或m≤-9,(12分)
所以实数m的取值范围为(-∞,-9]∪[1,+∞).(13分)
若选②,则A∩B= ,(10分)
所以m+1≤-2且m+7≥2,解得-5≤m≤-3,(12分)
所以实数m的取值范围为[-5,-3].(13分)
若选③,易得 RB=[m+1,m+7],(10分)
则m+1≤-2且m+7≥2,解得-5≤m≤-3,(12分)
所以实数m的取值范围为[-5,-3].(13分)
16.解析 (1)由频率分布直方图可知,5x=1-5×(0.07+0.04+0.02+0.01),
所以x=0.06.(2分)
因此身高在170 cm及以上的学生人数为100×(0.06×5+0.04×5+0.02×5)=60.(4分)
(2)身高在[170,175),[175,180),[180,185]内的学生人数分别为0.06×5×100=30,0.04×5×100=20,0.02×5×100=10,(6分)
因此应该从身高在[170,175),[175,180),[180,185]内的学生中分别抽取6×=3(人),6×=2(人),6×=1(人).(8分)
(3)在(2)的条件下,设身高在[170,175)内的3名学生分别为A1,A2,A3,身高在[175,180)内的2名学生分别为B1,B2,身高在[180,185]内的1名学生为C0,则从6名学生中抽取2人的样本点共15个,分别为(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C0),(A2,A3),(A2,B1),(A2,B2),(A2,C0),(A3,B1),(A3,B2),(A3,C0),(B1,B2),(B1,C0),(B2,C0),(11分)
至少有1人的身高在[175,180)内包含的样本点有9个,分别为(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C0),(B2,C0),(13分)
所以至少有1人的身高在[175,180)内的概率为.(15分)
17.解析 (1)填表如下:
v 40 60 90 100 120
Q 5.2 6 8.325 10 15.6
W 13 10 9.25 10 13
(3分)
由题意可得符合的函数模型需满足在40≤v≤120时有意义,且在[40,120]上单调递增.
Q(v)=0.5v+a在[40,120]上单调递减,不符合题意.(5分)
若选择Q(v)=av+b,代入(40,5.2),(60,6),
得
则Q(v)=0.04v+3.6,此时Q(90)=7.2,Q(100)=7.6,Q(120)=8.4,
与实际数据相差较大,所以不符合题意.(7分)
经观察,函数模型Q(v)=av3+bv2+cv最符合实际,(9分)
代入(40,5.2),(60,6),(100,10),
则
∴Q(v)=0.000 025v3-0.004v2+0.25v.(11分)
(2)∵W=×Q=0.002 5v2-0.4v+25=0.002 5(v-80)2+9,
∴当v=80时,W取得最小值9,(13分)
故该型号汽车在外侧车道以80 km/h的速度行驶时百公里耗油量最小. (15分)
18.解析 (1)由已知得h(x)=+tx-1,(2分)
任取x1,x2∈(0,2],且x1
要使h(x)在(0,2]上单调递减,只需h(x1)-h(x2)>0恒成立. (4分)
∵x2-x1>0,0
又∵,∴t≤,∴实数t的取值范围是.(8分)
(2)解法一:由f(x)
∵f(x)
∵-1,
∴当x=时,函数y=取得最小值3,∴<3.(15分)
又m>0,∴m>,∴正数m的取值范围是.(17分)
解法二:由f(x)
∴解得m>.(15分)
∴正数m的取值范围是.(17分)
19.解析 (1)由题意得,当x>0时,g(x)=log3x.
因为g(x)为R上的奇函数,所以g(0)=0,g(x)=-g(-x).
当x<0时,-x>0,所以g(x)=-g(-x)=-log3(-x).
综上,g(x)=(4分)
(2)①不等式3(log3x)2-20log9x+3≤0可化为3(log3x)2-10log3x+3≤0,
即(3log3x-1)(log3x-3)≤0,所以≤log3x≤3,解得≤x≤27,
所以集合A=[,27].(7分)
②h(x)=f·f·log3
=(log3x-a)(log3x-2)=(log3x)2-(a+2)log3x+2a.(9分)
设t=log3x,则t∈.(11分)
当,即a≤-时,函数s(t)在上单调递增,
所以s(t)min=s=-2,解得a=-(舍去);(13分)
当≥3,即a≥4时,函数s(t)在上单调递减,
所以s(t)min=s(3)=3-a=-2,解得a=5;(15分)
当<3,即-
解得a=2-2或a=2+2(舍去).
综上,实数a的值为2-2或5.(17分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
