人教版数学八年级下册20.1.2中位数和众数作业(含解析)
文档属性
| 名称 | 人教版数学八年级下册20.1.2中位数和众数作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 471.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 06:15:23 | ||
图片预览




文档简介
初中数学数据的集中趋势作业
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我市义务教育阶段所有公、民办学校,从2024年春季学期开始实行每天一节体育课,某同学统计了本周在校每天体育活动时间,列表如下:(单位:)
星期一 星期二 星期三 星期四 星期五
72 68 81 86 76
其中,本周在校每天体育活动时间的中位数是( )
A. B. C. D.
2.某校篮球队队员进行定点投篮训练,每人投篮10次,其中5名队员投中的次数分别是6,7,6,9,8,则这组数据的众数是( )
A.6 B.7 C.8 D.9
3.右表是某中学阳光社团 40 名志愿者的年龄分布统计表.对于 a 、b 取不同的值,下列关于 年龄的统计量不会发生改变的是( )
年龄(岁) 12 13 14 15
频数(名) 11 19 a b
A.平均数、众数 B.中位数、平均数
C.众数、中位数 D.平均数、方差
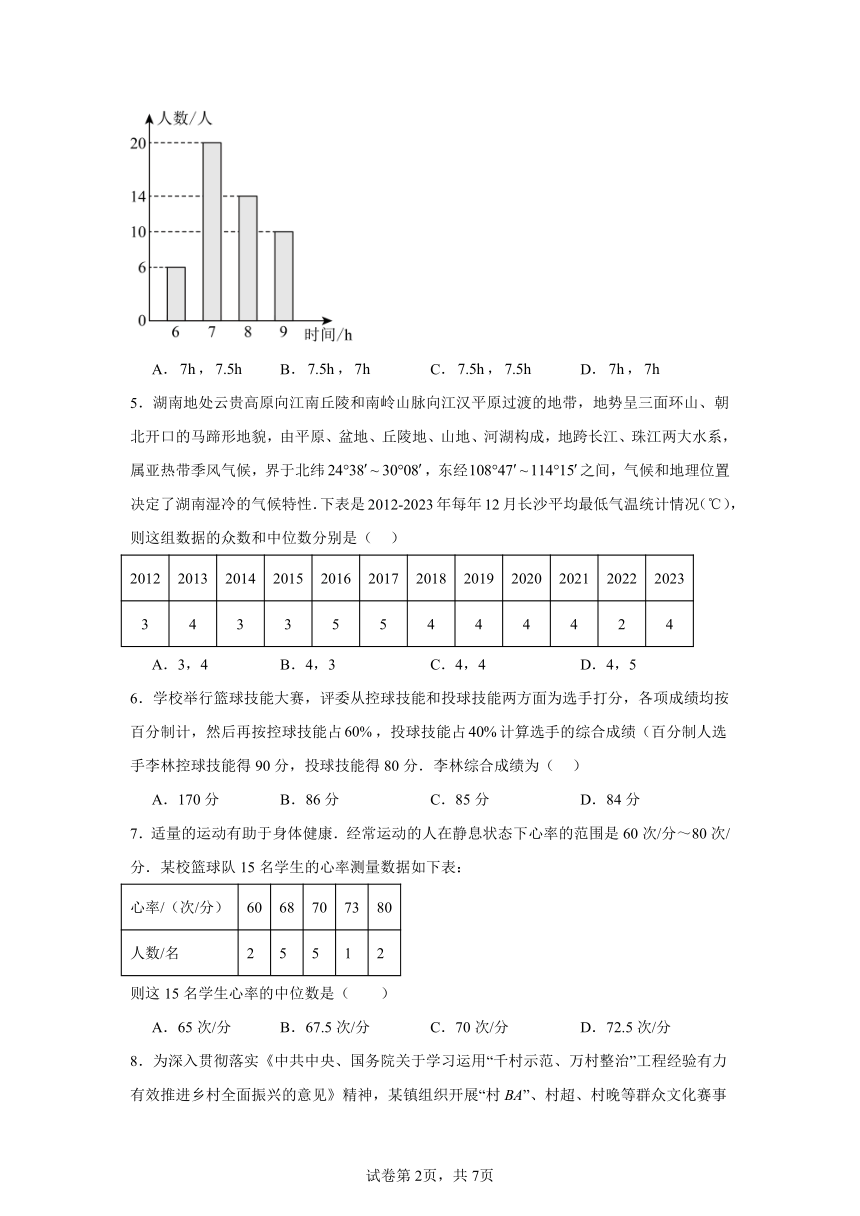
4.为督察学校落实学生每天在校“阳光锻炼一小时”要求,督察组调查了某校一个班 50 名学生每周体育课以外的锻炼时间,绘成如图所示的条形统计图,则所调查学生锻炼时间的众数和中位数分别为( )
A., B., C., D.,
5.湖南地处云贵高原向江南丘陵和南岭山脉向江汉平原过渡的地带,地势呈三面环山、朝北开口的马蹄形地貌,由平原、盆地、丘陵地、山地、河湖构成,地跨长江、珠江两大水系,属亚热带季风气候,界于北纬,东经之间,气候和地理位置决定了湖南湿冷的气候特性.下表是2012-2023年每年12月长沙平均最低气温统计情况(℃),则这组数据的众数和中位数分别是( )
2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023
3 4 3 3 5 5 4 4 4 4 2 4
A.3,4 B.4,3 C.4,4 D.4,5
6.学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩(百分制人选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
7.适量的运动有助于身体健康.经常运动的人在静息状态下心率的范围是60次/分~80次/分.某校篮球队15名学生的心率测量数据如下表:
心率/(次/分) 60 68 70 73 80
人数/名 2 5 5 1 2
则这15名学生心率的中位数是( )
A.65次/分 B.67.5次/分 C.70次/分 D.72.5次/分
8.为深入贯彻落实《中共中央、国务院关于学习运用“千村示范、万村整治”工程经验有力有效推进乡村全面振兴的意见》精神,某镇组织开展“村BA”、村超、村晚等群众文化赛事活动,其中参赛的六个村得分分别为:55,64,51,50,61,55,则这组数据的中位数是( )
A.53 B.55 C.58 D.64
9.某校学生期末美术成绩满分为,其中课堂表现占,平时绘画作业占,期末手工作品占,小花的三项成绩依次为,,,则小花的美术成绩为( )
A. B. C. D.
10.某班在阳光体育活动中,测试了五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据.在统计时,出现了一处错误:将最低成绩写得更低了,则计算结果不受影响的是( )
A.平均数 B.中位数 C.方差 D.极差
二、填空题
11.在排球比赛中,场上6名队员的身高分别是,,,,,.若教练将场上身高为的队员换成身高为的队员,则场上队员身高的平均数、众数、中位数中没有发生变化的是 .
12.若已知数据的平均数为a,那么数据,,的平均数为 (用含a的代数式表示).
13.某校“校园之声”社团招新时,需考查应聘学生的应变能力、知识储备、朗读水平三个项目,布布的三个项目得分分别为85分、90分、92分.若评委按照应变能力占,知识储备占,朗读水平占计算加权平均数来作为最终成绩,则布布的最终成绩为 分.
14.数据的平均数是1,则 .
15.某校组织学生进行数学素养测试,综合成绩是由数与代数、空间与图形、统计与概率、综合与实践的各项成绩按的比例计算所得.已知甲同学在数与代数、空间与图形、统计与概率、综合与实践的各项得分依次为92分、90分、95分、88分,则甲同学的数学综合成绩为 分.
16.某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:
项目 应聘者 综合知识 工作经验 语言表达
甲
乙
丙
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是 .
三、解答题
17.为了解A、B两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A、B两款智能玩具飞机各架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x表示,共分为三组:合格,中等,优等),下面给出了部分信息:
A款智能玩具飞机架一次充满电后运行最长时间是:
B款智能玩具飞机架一次充满电后运行最长时间属于中等的数据是:
两款智能玩具飞机运行最长时间统计表,B款智能玩具飞机运行最长时间扇形统计图
类别 A B
平均数
中位数 b
众数 a
方差
根据以上信息,解答下列问题:
(1)上述图表中___________,___________,___________;
(2)根据以上数据,你认为哪款智能玩具飞机运行性能更好?请说明理由(写出一条理由即可);
(3)若某玩具仓库有A款智能玩具飞机架、B款智能玩具飞机架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架?
18.端午节是中国的传统节日,民间有端午节吃粽子的习俗,在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按分制进行评分,成绩(单位:分)均为不低于的整数、为了解这次活动的效果,现从这两个年级各随机抽取名学生的活动成绩作为样本进行活整理,并绘制统计图表,部分信息如下:
八年级名学生活动成绩统计表
成绩/分
人数
已知八年级名学生活动成绩的中位数为分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为分的学生数是______________,七年级活动成绩的众数为______________分;
(2)______________,______________;
(3)若认定活动成绩不低于分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
19.为增强学生的社会实践能力,促进学生全面发展,某校计划建立小记者站,有20名学生报名参加选拔.报名的学生需参加采访、写作、摄影三项测试,每项测试均由七位评委打分(满分100分),取平均分作为该项的测试成绩,再将采访、写作、摄影三项的测试成绩按的比例计算出每人的总评成绩.
小悦、小涵的三项测试成绩和总评成绩如下表,这20名学生的总评成绩频数直方图(每组含最小值,不含最大值)如下图
选手 测试成绩/分 总评成绩/分
采访 写作 摄影
小悦 83 72 80 78
小涵 86 84 ▲ ▲
(1)在摄影测试中,七位评委给小涵打出的分数如下:67,72,68,69,74,69,71.这组数据的中位数是__________分,众数是__________分,平均数是__________分;
(2)请你计算小涵的总评成绩;
(3)学校决定根据总评成绩择优选拔12名小记者.试分析小悦、小涵能否入选,并说明理由.
20.跳绳是某校体育活动的特色项目.体育组为了了解七年级学生1分钟跳绳次数情况,随机抽取20名七年级学生进行1分钟跳绳测试(单位:次),数据如下:
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析,结果如下:
平均数 众数 中位数
145
请根据以上信息解答下列问题:
(1)填空:______,______;
(2)学校规定1分钟跳绳165次及以上为优秀,请你估计七年级240名学生中,约有多少名学生能达到优秀?
(3)某同学1分钟跳绳152次,请推测该同学的1分钟跳绳次数是否超过年级一半的学生?说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了确定一组数据的中位数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.根据中位数的定义直接解答即可.
【详解】解:这组数据从小到大排列为68,72,76,81,86,
则本周每天体育活动时间的中位数是,
故选:B.
2.A
【分析】根据数组中出现次数最多的数据是众数解答.本题考查了众数,掌握众数的定义意义是解题的关键.
【详解】解:6出现次数最多,则众数是6,
故选:A.
3.C
【分析】本题主要考查众数和中位数,熟练掌握中位数、众数的定是解题的关键.
由频数分布表可知年龄14岁和年龄15岁的两组的频数和为10,结合前两组的频数知出现次数是11,19个数据的平均数,然后中位数、众数的定即可解答.
【详解】解:由表可知,年龄为14岁与年龄为15岁的频数和为,
由频数分布表可知:出现次数最多的是13岁,和中位数出现在13岁年龄段,不会因a 、b 取不同的值而变化.
故选:C.
4.D
【分析】本题主要考查了众数、中位数的概念,直接利用众数以及中位数的概念分别分析求出即可,正确把握中位数的概念是解题关键.
【详解】∵出现了20次,出现的次数最多,
∴所调查学生睡眠时间的众数是,
∵共有50名学生,中位数是第25、26个数的平均数,
∴所调查学生睡眠时间的中位数是,
故选:D.
5.C
【分析】本题考查中位数和众数,根据中位数是将数据排序后,位于中间一位或两位的平均数,众数为一组数据中出现次数最多的数据,进行求解即可.
【详解】解:出现次数最多的数据为4,故众数为4,
将数据排序后,位于第6个和第7个数据均为4,故中位数为4;
故选C.
6.B
【分析】本题考查求加权平均数,利用加权平均数的计算方法,进行求解即可.
【详解】解:(分);
故选B.
7.C
【分析】本题考查了确定一组数据的中位数,找中位数的时候一定要先将数据排好顺序,如果数据有奇数个,则正中间的数字即为所求;如果数据有偶数个,则找中间两位数的平均数.
【详解】解:∵共有15名学生,中位数是第8个数,
∴这15名学生心率的中位数是70次/分;
故选:C.
8.B
【分析】本题主要考查了中位数的定义,根据中位数的定义求解即可.
【详解】解:参赛的六个村得分分别为:55,64,51,50,61,55,
把这6个数从小到大排序:50,51,55,55,61,64,
∴这组数据的中位数是:,
故选:B.
9.D
【分析】本题考查了加权平均数的求法,根据加权平均数的计算方法进行计算即可,解题的关键是理解题意,正确计算.
【详解】解:
,
,
故选:.
10.B
【分析】本题主要考查方差、极差、中位数和平均数,根据中位数的定义解答可得.
【详解】解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最低成绩写得更低了,计算结果不受影响的是中位数,
故选:B.
11.众数
【分析】本题考查平均数、众数,中位数,解题的关键是掌握平均数和众数的定义.平均数等于一组数据中所有数据之和再除以这组数据的个数;众数指一组数据中出现次数最多的数;中位数指一组数据按顺序排列,居于中间位置的数;根据平均数、众数,中位数的定义判断即可.
【详解】解:若将场上身高为的队员换成身高为的队员,
则6名队员身高的和变大,因此平均数变大;
出现次数最多的数据依然是,因此众数不变;
∵原数据从小到大排列:,,,,,,中位数是,
原数据从小到大排列:,, ,,,,中位数是,
∴中位数变大.
∴没有发生变化的是众数.
故答案为:众数.
12.
【分析】根据平均数的性质知,要求,,的平均数,只要把数,,的和表示出即可.
本题考查的是平均数的求法.解决本题的关键是用一组数据的平均数表示另一组数据的平均数.
【详解】由题意得,数据的平均数为
则
则数据,,的平均数为
故答案为:.
13.90
【分析】本题主要考查了求加权平均数,根据加权平均数的计算公式进行计算即可.
【详解】解:布布的最终成绩为:
,
故答案为:90.
14.
【分析】本题主要考查了平均数,理解并掌握平均数的定义是解题关键.根据平均数的定义列出方程,解方程可得答案.
【详解】解:根据题意,可得,
解得.
故答案为:.
15.
【分析】此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键.利用加权平均数公式直接计算即可.
【详解】解:甲的数学综合成绩分,
故答案为:
16.乙
【分析】分别计算甲、乙、丙三名应聘者的成绩的加权平均数,比较大小即可求解.
【详解】解:,
,
,
∵
∴被录用的是乙,
故答案为:乙.
【点睛】本题考查了加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
17.(1),,;
(2)B款智能玩具飞机运行性能更好;因为B款智能玩具飞机运行时间的方差比A款智能玩具飞机运行时间的方差小,运行时间比较稳定;
(3)两款智能玩具飞机运行性能在中等及以上的大约共有架.
【分析】(1)由A款数据可得A款的众数,即可求出,由B款扇形数据可求得合格数及优秀数,从而求得中位数及优秀等次的百分比;
(2)根据方差越小越稳定即可判断;
(3)用样本数据估计总体,分别求出两款飞机中等及以上的架次相加即可.
【详解】(1)解:由题意可知架A款智能玩具飞机充满电后运行最长时间中,只有出现了三次,且次数最多,则该组数据的众数为,即;
由B款智能玩具飞机运行时间的扇形图可知,合格的百分比为,
则B款智能玩具飞机运行时间合格的架次为:(架)
则B款智能玩具飞机运行时间优等的架次为:(架)
则B款智能玩具飞机的运行时间第五、第六个数据分别为:,
故B款智能玩具飞机运行时间的中位数为:
B款智能玩具飞机运行时间优等的百分比为:
即
故答案为:,,;
(2)B款智能玩具飞机运行性能更好;因为B款智能玩具飞机运行时间的方差比A款智能玩具飞机运行时间的方差小,运行时间比较稳定;
(3)架A款智能玩具飞机运行性能在中等及以上的架次为:
(架)
架B款智能玩具飞机运行性能在中等及以上的架次为:
(架)
则两款智能玩具飞机运行性能在中等及以上的共有:架,
答:两款智能玩具飞机运行性能在中等及以上的大约共有架.
【点睛】本题考查了扇形统计图,中位数、众数、百分比,用方差做决策,用样本估计总体;解题的关键是熟练掌握相关知识综合求解.
18.(1)
(2)
(3)优秀率高的年级不是平均成绩也高,理由见解析
【分析】(1)根据扇形统计图得出七年级活动成绩为分的学生数的占比为,即可得出七年级活动成绩为分的学生数,根据扇形统计图结合众数的定义,即可求解;
(2)根据中位数的定义,得出第名学生为分,第名学生为分,进而求得,的值,即可求解;
(3)分别求得七年级与八年级的优秀率与平均成绩,即可求解.
【详解】(1)解:根据扇形统计图,七年级活动成绩为分的学生数的占比为
∴样本中,七年级活动成绩为分的学生数是,
根据扇形统计图,七年级活动成绩的众数为
故答案为:.
(2)∵八年级名学生活动成绩的中位数为分,
第名学生为分,第名学生为分,
∴,
,
故答案为:.
(3)优秀率高的年级不是平均成绩也高,理由如下,
七年级优秀率为,平均成绩为:,
八年级优秀率为,平均成绩为:,
∴优秀率高的年级为八年级,但平均成绩七年级更高,
∴优秀率高的年级不是平均成绩也高
【点睛】本题考查了扇形统计图,统计表,中位数,众数,求一组数据的平均数,从统计图表获取信息是解题的关键.
19.(1)69,69,70
(2)82分
(3)小涵能入选,小悦不一定能入选,见解析
【分析】(1)从小到大排序,找出中位数、众数即可,算出平均数.
(2)将采访、写作、摄影三项的测试成绩按的比例计算出的总评成绩即可.
(3)小涵和小悦的总评成绩分别是82分,78分,学校要选拔12名小记者,小涵的成绩在前12名,因此小涵一定能入选;小悦的成绩不一定在前12名,因此小悦不一定能入选.
【详解】(1)从小到大排序,
67,68,69,69,71,72, 74,
∴中位数是69,
众数是69,
平均数:
69,69,70
(2)解:(分).
答:小涵的总评成绩为82分.
(3)结论:小涵能入选,小悦不一定能入选
理由:由频数直方图可得,总评成绩不低于80分的学生有10名,总评成绩不低于70分且小宁80分的学生有6名.小涵和小悦的总评成绩分别是82分,78分,学校要选拔12名小记者,小涵的成绩在前12名,因此小涵一定能入选;小悦的成绩不一定在前12名,因此小悦不一定能入选.
【点睛】此题考查了中位数、众数、平均数,解题的关键是熟悉相关概念.
20.(1),
(2)
(3)是,理由见解析
【分析】(1)根据众数与中位数的定义进行计算即可求解;
(2)根据样本估计总体,用跳绳165次及以上人数的占比乘以总人数,即可求解;
(3)根据中位数的定义即可求解;
【详解】(1)解:这组数据中,165出现了4次,出现次数最多
∴,
这组数据从小到大排列,第10个和11个数据分别为,
∴,
故答案为:,.
(2)解:∵跳绳165次及以上人数有7个,
∴估计七年级240名学生中,有个优秀,
(3)解:∵中位数为,
∴某同学1分钟跳绳152次,可推测该同学的1分钟跳绳次数超过年级一半的学生.
【点睛】本题考查了求中位数,众数,样本估计总体,熟练掌握中位数、众数的定义是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我市义务教育阶段所有公、民办学校,从2024年春季学期开始实行每天一节体育课,某同学统计了本周在校每天体育活动时间,列表如下:(单位:)
星期一 星期二 星期三 星期四 星期五
72 68 81 86 76
其中,本周在校每天体育活动时间的中位数是( )
A. B. C. D.
2.某校篮球队队员进行定点投篮训练,每人投篮10次,其中5名队员投中的次数分别是6,7,6,9,8,则这组数据的众数是( )
A.6 B.7 C.8 D.9
3.右表是某中学阳光社团 40 名志愿者的年龄分布统计表.对于 a 、b 取不同的值,下列关于 年龄的统计量不会发生改变的是( )
年龄(岁) 12 13 14 15
频数(名) 11 19 a b
A.平均数、众数 B.中位数、平均数
C.众数、中位数 D.平均数、方差
4.为督察学校落实学生每天在校“阳光锻炼一小时”要求,督察组调查了某校一个班 50 名学生每周体育课以外的锻炼时间,绘成如图所示的条形统计图,则所调查学生锻炼时间的众数和中位数分别为( )
A., B., C., D.,
5.湖南地处云贵高原向江南丘陵和南岭山脉向江汉平原过渡的地带,地势呈三面环山、朝北开口的马蹄形地貌,由平原、盆地、丘陵地、山地、河湖构成,地跨长江、珠江两大水系,属亚热带季风气候,界于北纬,东经之间,气候和地理位置决定了湖南湿冷的气候特性.下表是2012-2023年每年12月长沙平均最低气温统计情况(℃),则这组数据的众数和中位数分别是( )
2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023
3 4 3 3 5 5 4 4 4 4 2 4
A.3,4 B.4,3 C.4,4 D.4,5
6.学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩(百分制人选手李林控球技能得90分,投球技能得80分.李林综合成绩为( )
A.170分 B.86分 C.85分 D.84分
7.适量的运动有助于身体健康.经常运动的人在静息状态下心率的范围是60次/分~80次/分.某校篮球队15名学生的心率测量数据如下表:
心率/(次/分) 60 68 70 73 80
人数/名 2 5 5 1 2
则这15名学生心率的中位数是( )
A.65次/分 B.67.5次/分 C.70次/分 D.72.5次/分
8.为深入贯彻落实《中共中央、国务院关于学习运用“千村示范、万村整治”工程经验有力有效推进乡村全面振兴的意见》精神,某镇组织开展“村BA”、村超、村晚等群众文化赛事活动,其中参赛的六个村得分分别为:55,64,51,50,61,55,则这组数据的中位数是( )
A.53 B.55 C.58 D.64
9.某校学生期末美术成绩满分为,其中课堂表现占,平时绘画作业占,期末手工作品占,小花的三项成绩依次为,,,则小花的美术成绩为( )
A. B. C. D.
10.某班在阳光体育活动中,测试了五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据.在统计时,出现了一处错误:将最低成绩写得更低了,则计算结果不受影响的是( )
A.平均数 B.中位数 C.方差 D.极差
二、填空题
11.在排球比赛中,场上6名队员的身高分别是,,,,,.若教练将场上身高为的队员换成身高为的队员,则场上队员身高的平均数、众数、中位数中没有发生变化的是 .
12.若已知数据的平均数为a,那么数据,,的平均数为 (用含a的代数式表示).
13.某校“校园之声”社团招新时,需考查应聘学生的应变能力、知识储备、朗读水平三个项目,布布的三个项目得分分别为85分、90分、92分.若评委按照应变能力占,知识储备占,朗读水平占计算加权平均数来作为最终成绩,则布布的最终成绩为 分.
14.数据的平均数是1,则 .
15.某校组织学生进行数学素养测试,综合成绩是由数与代数、空间与图形、统计与概率、综合与实践的各项成绩按的比例计算所得.已知甲同学在数与代数、空间与图形、统计与概率、综合与实践的各项得分依次为92分、90分、95分、88分,则甲同学的数学综合成绩为 分.
16.某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:
项目 应聘者 综合知识 工作经验 语言表达
甲
乙
丙
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是 .
三、解答题
17.为了解A、B两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A、B两款智能玩具飞机各架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x表示,共分为三组:合格,中等,优等),下面给出了部分信息:
A款智能玩具飞机架一次充满电后运行最长时间是:
B款智能玩具飞机架一次充满电后运行最长时间属于中等的数据是:
两款智能玩具飞机运行最长时间统计表,B款智能玩具飞机运行最长时间扇形统计图
类别 A B
平均数
中位数 b
众数 a
方差
根据以上信息,解答下列问题:
(1)上述图表中___________,___________,___________;
(2)根据以上数据,你认为哪款智能玩具飞机运行性能更好?请说明理由(写出一条理由即可);
(3)若某玩具仓库有A款智能玩具飞机架、B款智能玩具飞机架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架?
18.端午节是中国的传统节日,民间有端午节吃粽子的习俗,在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按分制进行评分,成绩(单位:分)均为不低于的整数、为了解这次活动的效果,现从这两个年级各随机抽取名学生的活动成绩作为样本进行活整理,并绘制统计图表,部分信息如下:
八年级名学生活动成绩统计表
成绩/分
人数
已知八年级名学生活动成绩的中位数为分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为分的学生数是______________,七年级活动成绩的众数为______________分;
(2)______________,______________;
(3)若认定活动成绩不低于分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
19.为增强学生的社会实践能力,促进学生全面发展,某校计划建立小记者站,有20名学生报名参加选拔.报名的学生需参加采访、写作、摄影三项测试,每项测试均由七位评委打分(满分100分),取平均分作为该项的测试成绩,再将采访、写作、摄影三项的测试成绩按的比例计算出每人的总评成绩.
小悦、小涵的三项测试成绩和总评成绩如下表,这20名学生的总评成绩频数直方图(每组含最小值,不含最大值)如下图
选手 测试成绩/分 总评成绩/分
采访 写作 摄影
小悦 83 72 80 78
小涵 86 84 ▲ ▲
(1)在摄影测试中,七位评委给小涵打出的分数如下:67,72,68,69,74,69,71.这组数据的中位数是__________分,众数是__________分,平均数是__________分;
(2)请你计算小涵的总评成绩;
(3)学校决定根据总评成绩择优选拔12名小记者.试分析小悦、小涵能否入选,并说明理由.
20.跳绳是某校体育活动的特色项目.体育组为了了解七年级学生1分钟跳绳次数情况,随机抽取20名七年级学生进行1分钟跳绳测试(单位:次),数据如下:
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析,结果如下:
平均数 众数 中位数
145
请根据以上信息解答下列问题:
(1)填空:______,______;
(2)学校规定1分钟跳绳165次及以上为优秀,请你估计七年级240名学生中,约有多少名学生能达到优秀?
(3)某同学1分钟跳绳152次,请推测该同学的1分钟跳绳次数是否超过年级一半的学生?说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题考查了确定一组数据的中位数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.根据中位数的定义直接解答即可.
【详解】解:这组数据从小到大排列为68,72,76,81,86,
则本周每天体育活动时间的中位数是,
故选:B.
2.A
【分析】根据数组中出现次数最多的数据是众数解答.本题考查了众数,掌握众数的定义意义是解题的关键.
【详解】解:6出现次数最多,则众数是6,
故选:A.
3.C
【分析】本题主要考查众数和中位数,熟练掌握中位数、众数的定是解题的关键.
由频数分布表可知年龄14岁和年龄15岁的两组的频数和为10,结合前两组的频数知出现次数是11,19个数据的平均数,然后中位数、众数的定即可解答.
【详解】解:由表可知,年龄为14岁与年龄为15岁的频数和为,
由频数分布表可知:出现次数最多的是13岁,和中位数出现在13岁年龄段,不会因a 、b 取不同的值而变化.
故选:C.
4.D
【分析】本题主要考查了众数、中位数的概念,直接利用众数以及中位数的概念分别分析求出即可,正确把握中位数的概念是解题关键.
【详解】∵出现了20次,出现的次数最多,
∴所调查学生睡眠时间的众数是,
∵共有50名学生,中位数是第25、26个数的平均数,
∴所调查学生睡眠时间的中位数是,
故选:D.
5.C
【分析】本题考查中位数和众数,根据中位数是将数据排序后,位于中间一位或两位的平均数,众数为一组数据中出现次数最多的数据,进行求解即可.
【详解】解:出现次数最多的数据为4,故众数为4,
将数据排序后,位于第6个和第7个数据均为4,故中位数为4;
故选C.
6.B
【分析】本题考查求加权平均数,利用加权平均数的计算方法,进行求解即可.
【详解】解:(分);
故选B.
7.C
【分析】本题考查了确定一组数据的中位数,找中位数的时候一定要先将数据排好顺序,如果数据有奇数个,则正中间的数字即为所求;如果数据有偶数个,则找中间两位数的平均数.
【详解】解:∵共有15名学生,中位数是第8个数,
∴这15名学生心率的中位数是70次/分;
故选:C.
8.B
【分析】本题主要考查了中位数的定义,根据中位数的定义求解即可.
【详解】解:参赛的六个村得分分别为:55,64,51,50,61,55,
把这6个数从小到大排序:50,51,55,55,61,64,
∴这组数据的中位数是:,
故选:B.
9.D
【分析】本题考查了加权平均数的求法,根据加权平均数的计算方法进行计算即可,解题的关键是理解题意,正确计算.
【详解】解:
,
,
故选:.
10.B
【分析】本题主要考查方差、极差、中位数和平均数,根据中位数的定义解答可得.
【详解】解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最低成绩写得更低了,计算结果不受影响的是中位数,
故选:B.
11.众数
【分析】本题考查平均数、众数,中位数,解题的关键是掌握平均数和众数的定义.平均数等于一组数据中所有数据之和再除以这组数据的个数;众数指一组数据中出现次数最多的数;中位数指一组数据按顺序排列,居于中间位置的数;根据平均数、众数,中位数的定义判断即可.
【详解】解:若将场上身高为的队员换成身高为的队员,
则6名队员身高的和变大,因此平均数变大;
出现次数最多的数据依然是,因此众数不变;
∵原数据从小到大排列:,,,,,,中位数是,
原数据从小到大排列:,, ,,,,中位数是,
∴中位数变大.
∴没有发生变化的是众数.
故答案为:众数.
12.
【分析】根据平均数的性质知,要求,,的平均数,只要把数,,的和表示出即可.
本题考查的是平均数的求法.解决本题的关键是用一组数据的平均数表示另一组数据的平均数.
【详解】由题意得,数据的平均数为
则
则数据,,的平均数为
故答案为:.
13.90
【分析】本题主要考查了求加权平均数,根据加权平均数的计算公式进行计算即可.
【详解】解:布布的最终成绩为:
,
故答案为:90.
14.
【分析】本题主要考查了平均数,理解并掌握平均数的定义是解题关键.根据平均数的定义列出方程,解方程可得答案.
【详解】解:根据题意,可得,
解得.
故答案为:.
15.
【分析】此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键.利用加权平均数公式直接计算即可.
【详解】解:甲的数学综合成绩分,
故答案为:
16.乙
【分析】分别计算甲、乙、丙三名应聘者的成绩的加权平均数,比较大小即可求解.
【详解】解:,
,
,
∵
∴被录用的是乙,
故答案为:乙.
【点睛】本题考查了加权平均数,熟练掌握加权平均数的计算方法是解题的关键.
17.(1),,;
(2)B款智能玩具飞机运行性能更好;因为B款智能玩具飞机运行时间的方差比A款智能玩具飞机运行时间的方差小,运行时间比较稳定;
(3)两款智能玩具飞机运行性能在中等及以上的大约共有架.
【分析】(1)由A款数据可得A款的众数,即可求出,由B款扇形数据可求得合格数及优秀数,从而求得中位数及优秀等次的百分比;
(2)根据方差越小越稳定即可判断;
(3)用样本数据估计总体,分别求出两款飞机中等及以上的架次相加即可.
【详解】(1)解:由题意可知架A款智能玩具飞机充满电后运行最长时间中,只有出现了三次,且次数最多,则该组数据的众数为,即;
由B款智能玩具飞机运行时间的扇形图可知,合格的百分比为,
则B款智能玩具飞机运行时间合格的架次为:(架)
则B款智能玩具飞机运行时间优等的架次为:(架)
则B款智能玩具飞机的运行时间第五、第六个数据分别为:,
故B款智能玩具飞机运行时间的中位数为:
B款智能玩具飞机运行时间优等的百分比为:
即
故答案为:,,;
(2)B款智能玩具飞机运行性能更好;因为B款智能玩具飞机运行时间的方差比A款智能玩具飞机运行时间的方差小,运行时间比较稳定;
(3)架A款智能玩具飞机运行性能在中等及以上的架次为:
(架)
架B款智能玩具飞机运行性能在中等及以上的架次为:
(架)
则两款智能玩具飞机运行性能在中等及以上的共有:架,
答:两款智能玩具飞机运行性能在中等及以上的大约共有架.
【点睛】本题考查了扇形统计图,中位数、众数、百分比,用方差做决策,用样本估计总体;解题的关键是熟练掌握相关知识综合求解.
18.(1)
(2)
(3)优秀率高的年级不是平均成绩也高,理由见解析
【分析】(1)根据扇形统计图得出七年级活动成绩为分的学生数的占比为,即可得出七年级活动成绩为分的学生数,根据扇形统计图结合众数的定义,即可求解;
(2)根据中位数的定义,得出第名学生为分,第名学生为分,进而求得,的值,即可求解;
(3)分别求得七年级与八年级的优秀率与平均成绩,即可求解.
【详解】(1)解:根据扇形统计图,七年级活动成绩为分的学生数的占比为
∴样本中,七年级活动成绩为分的学生数是,
根据扇形统计图,七年级活动成绩的众数为
故答案为:.
(2)∵八年级名学生活动成绩的中位数为分,
第名学生为分,第名学生为分,
∴,
,
故答案为:.
(3)优秀率高的年级不是平均成绩也高,理由如下,
七年级优秀率为,平均成绩为:,
八年级优秀率为,平均成绩为:,
∴优秀率高的年级为八年级,但平均成绩七年级更高,
∴优秀率高的年级不是平均成绩也高
【点睛】本题考查了扇形统计图,统计表,中位数,众数,求一组数据的平均数,从统计图表获取信息是解题的关键.
19.(1)69,69,70
(2)82分
(3)小涵能入选,小悦不一定能入选,见解析
【分析】(1)从小到大排序,找出中位数、众数即可,算出平均数.
(2)将采访、写作、摄影三项的测试成绩按的比例计算出的总评成绩即可.
(3)小涵和小悦的总评成绩分别是82分,78分,学校要选拔12名小记者,小涵的成绩在前12名,因此小涵一定能入选;小悦的成绩不一定在前12名,因此小悦不一定能入选.
【详解】(1)从小到大排序,
67,68,69,69,71,72, 74,
∴中位数是69,
众数是69,
平均数:
69,69,70
(2)解:(分).
答:小涵的总评成绩为82分.
(3)结论:小涵能入选,小悦不一定能入选
理由:由频数直方图可得,总评成绩不低于80分的学生有10名,总评成绩不低于70分且小宁80分的学生有6名.小涵和小悦的总评成绩分别是82分,78分,学校要选拔12名小记者,小涵的成绩在前12名,因此小涵一定能入选;小悦的成绩不一定在前12名,因此小悦不一定能入选.
【点睛】此题考查了中位数、众数、平均数,解题的关键是熟悉相关概念.
20.(1),
(2)
(3)是,理由见解析
【分析】(1)根据众数与中位数的定义进行计算即可求解;
(2)根据样本估计总体,用跳绳165次及以上人数的占比乘以总人数,即可求解;
(3)根据中位数的定义即可求解;
【详解】(1)解:这组数据中,165出现了4次,出现次数最多
∴,
这组数据从小到大排列,第10个和11个数据分别为,
∴,
故答案为:,.
(2)解:∵跳绳165次及以上人数有7个,
∴估计七年级240名学生中,有个优秀,
(3)解:∵中位数为,
∴某同学1分钟跳绳152次,可推测该同学的1分钟跳绳次数超过年级一半的学生.
【点睛】本题考查了求中位数,众数,样本估计总体,熟练掌握中位数、众数的定义是解题的关键.
答案第1页,共2页
答案第1页,共2页
