苏教版五年级数学下册第7单元 解决问题的策略7.2 解决问题的策略(2)(课件)(共31张PPT)
文档属性
| 名称 | 苏教版五年级数学下册第7单元 解决问题的策略7.2 解决问题的策略(2)(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
第 2课时 | 解决问题的策略(2)
第七单元 解决问题的策略
任 课 教 师 | X X X
苏教版五年级数学下册
知识无涯,进步无界!
小学数学小班化“1+1”教学模式
新理念
新模式
新课标
新征程
教 学 重 点
1、用转化策略解决相关计算。
1
教 学 难 点
1、理解算式转化的依据和方法。
2、进一步感受和认识转化的策略,能根据一些算式的特点,采用转化策略用简便的方法计算得数;能发现一些计算的规律,并能应用规律简便计算。
2
重点难点
知
界
无
识
知识无涯,进步无界!
亲爱的同学们,请开始
你的读学内容,带着问题把你的读学困惑记录下来吧!
预
习
读
学
内
容
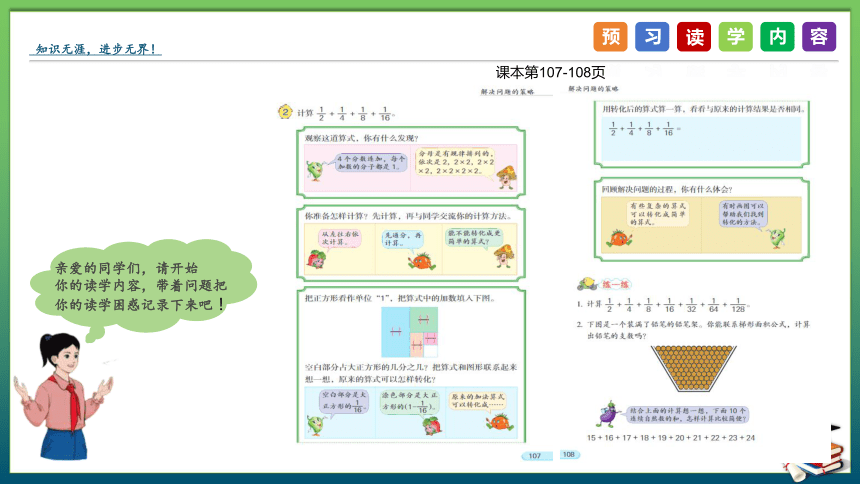
课本第107-108页
个人读学困惑 记录表 问题 困惑内容
问题1
问题2
问题3
问题4
知识无涯,进步无界!
预
学
读
习
小组读学困惑 汇总表 困惑学生姓名 问题 困惑内容
问题1
问题2
问题3
问题4
问题5
问题6
知识无涯,进步无界!
团
学
互
队
古时候,司马光与伙伴玩耍,突然,他看见一孩童不慎落入深缸。众孩惊慌,司马光却冷静应对。他迅速搬起石头,用力砸向缸壁,水流涌出,孩童得救。此事传为佳话,展现了司马光的机智与果断。他的勇敢与智慧,成为后人学习的榜样。
说一说:司马光砸缸的故事中,司马光是怎么思考的呢?
正常来讲要让人离开水。
这节课我们继续学习转化的思想。
但因为实际情况做不到,便运用逆向思维,将人离开水转化为水离开人。
4个分数连加,每个加数的分子都是1。
分母是有规律排列的,依次是2, 2×2, 2×2×2, 2×2×2×2。
观察这道算式, 你有什么发现?
计算 。
1
1
1
1
2×2
4×2
8×2
后一个分数总是前一个分数的 。
(教材P107 例2)
你准备怎样计算?先计算,
再与同学交流你的计算方法。
方法一:从左往右依次计算。
3
4
=
7
8
=
15
16
=
方法二:先通分,再计算。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
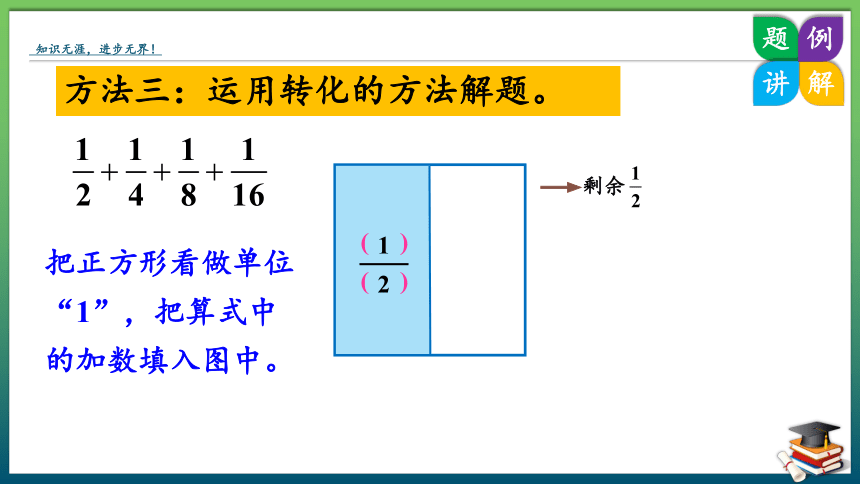
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
( )
( )
( )
( )
1
16
空白部分占大正方形的几分之几?
1
16
方法三:运用转化的方法解题。
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
把算式和图形联系起来想一想,原来的算式可以怎样转化?
涂色部分的总和
=
单位“1”
-
空白部分
转化后的计算结果和原来的计算结果是否相同?
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
思考:
1.为什么可以转化成减法计算?
2.转化后的计算和原来比,你有什么感受?
涂色部分=“1”-空白部分
转化后计算更简便。
想一想,说一说:在刚才的解题过程中,有哪些体会和发现?
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
照这个规律就算一直加下去,永远比1小。
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
我们可以根据转化的策略进行简便计算。
教
惑
解
师
知识无涯,进步无界!
01
02
在这堂课的学习中,你的“预习读学”的困惑问题
得到解决了吗?
在这堂课的学习过程中,你还有什么困惑吗?
请提出来,我们一起来解决。
小采访
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
第 2课时 | 解决问题的策略(2)
第七单元 解决问题的策略
任 课 教 师 | X X X
苏教版五年级数学下册
知识无涯,进步无界!
小学数学小班化“1+1”教学模式
新理念
新模式
新课标
新征程
教 学 重 点
1、用转化策略解决相关计算。
1
教 学 难 点
1、理解算式转化的依据和方法。
2、进一步感受和认识转化的策略,能根据一些算式的特点,采用转化策略用简便的方法计算得数;能发现一些计算的规律,并能应用规律简便计算。
2
重点难点
知
界
无
识
知识无涯,进步无界!
亲爱的同学们,请开始
你的读学内容,带着问题把你的读学困惑记录下来吧!
预
习
读
学
内
容
课本第107-108页
个人读学困惑 记录表 问题 困惑内容
问题1
问题2
问题3
问题4
知识无涯,进步无界!
预
学
读
习
小组读学困惑 汇总表 困惑学生姓名 问题 困惑内容
问题1
问题2
问题3
问题4
问题5
问题6
知识无涯,进步无界!
团
学
互
队
古时候,司马光与伙伴玩耍,突然,他看见一孩童不慎落入深缸。众孩惊慌,司马光却冷静应对。他迅速搬起石头,用力砸向缸壁,水流涌出,孩童得救。此事传为佳话,展现了司马光的机智与果断。他的勇敢与智慧,成为后人学习的榜样。
说一说:司马光砸缸的故事中,司马光是怎么思考的呢?
正常来讲要让人离开水。
这节课我们继续学习转化的思想。
但因为实际情况做不到,便运用逆向思维,将人离开水转化为水离开人。
4个分数连加,每个加数的分子都是1。
分母是有规律排列的,依次是2, 2×2, 2×2×2, 2×2×2×2。
观察这道算式, 你有什么发现?
计算 。
1
1
1
1
2×2
4×2
8×2
后一个分数总是前一个分数的 。
(教材P107 例2)
你准备怎样计算?先计算,
再与同学交流你的计算方法。
方法一:从左往右依次计算。
3
4
=
7
8
=
15
16
=
方法二:先通分,再计算。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
方法三:运用转化的方法解题。
把正方形看做单位“1”,把算式中的加数填入图中。
( )
( )
1
2
剩余
( )
( )
1
4
( )
( )
1
8
剩余
剩余
( )
( )
( )
( )
1
16
空白部分占大正方形的几分之几?
1
16
方法三:运用转化的方法解题。
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
把算式和图形联系起来想一想,原来的算式可以怎样转化?
涂色部分的总和
=
单位“1”
-
空白部分
转化后的计算结果和原来的计算结果是否相同?
( )
( )
1
2
( )
( )
1
4
( )
( )
1
8
( )
( )
1
16
思考:
1.为什么可以转化成减法计算?
2.转化后的计算和原来比,你有什么感受?
涂色部分=“1”-空白部分
转化后计算更简便。
想一想,说一说:在刚才的解题过程中,有哪些体会和发现?
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
照这个规律就算一直加下去,永远比1小。
有些复杂的算式可以转化成简单的算式。
有时画图可以帮助我们找到转化的方法。
我们可以根据转化的策略进行简便计算。
教
惑
解
师
知识无涯,进步无界!
01
02
在这堂课的学习中,你的“预习读学”的困惑问题
得到解决了吗?
在这堂课的学习过程中,你还有什么困惑吗?
请提出来,我们一起来解决。
小采访
这堂课,
你一定收获满满了吧?
请跟同学一起分享你的收获吧!
知识无涯,进步无界!
我
享
分
会
学
本课结束 感谢聆听!
