数学人教A版(2019)必修第二册9.1.2分层随机抽样 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册9.1.2分层随机抽样 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 09:06:33 | ||
图片预览








文档简介
(共21张PPT)
9.1.2分层随机抽样
学习目标
通过实例了解分层随机抽样的概念、特点和操作步骤
01
掌握各层样本量化比例分配的方法
02
03
掌握分层抽样中样本平均数与总体平均数的计算方法
1. 简单随机抽样的概念:
简单随机抽样的特点:
2. 简单随机抽样的常用方法:
③机会均等.
①总体有限个;
②逐个抽取;
①抽签法;
②随机数表法
设一个总体含有有限个个体,并记其个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的机会相等,就称这样的抽样为简单随机抽样.
3. 总体均值与样本均值
用样本的平均数估计总体的平均数
新知探究
新知探究
问1:在高一年级的712名学生中,男生有326名, 女生有386名,现要了解全体高一年级学生的平均身高,要从中抽取一个容量为50的样本.
追问:会不会出现“极端样本”,50个个体大部分来自高个子或矮个子的 情形?
新知探究
问2:是否对男生、女生分别进行简单随机抽样?
追问:如何抽才能更加准确?
为了使样本的结构与总体的分布相近,人数多的群体应多抽一些,人数少的群体应少抽一些.
即可按男生、女生在全体学生中所占的比例进行分配:
新知探究
男生样本量=
男生人数
全体学生数
×总样本量
女生样本量=
女生人数
全体学生数
×总样本量
无论男生、女生,每个学生被抽到的概率都相等.
均为
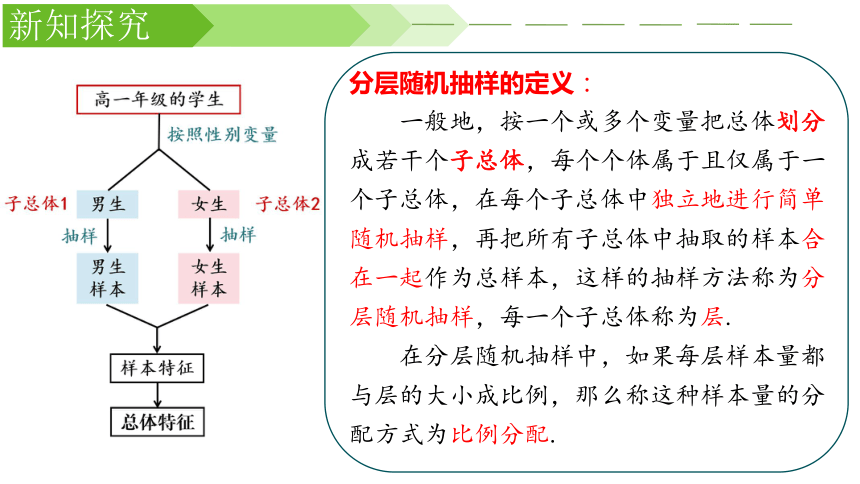
分层随机抽样的定义:
一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样,每一个子总体称为层.
在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.
新知探究
分层随机抽样的步骤:
分层
按某种特征将总体分成若干部分(层)
计算
抽样比
抽样比
定数
按抽样比确定每层抽取的个体数=每层数量×
抽样
各层分别按简单随机抽样的方法抽取样本
汇总
综合各层抽样,组成样本
新知探究
练习:某中学有老年教师20人,中年教师65人,青年教师95人,为了调查他们的健康状况,需从他们中抽取一个样本容量为36的样本,则合适的抽样方法是( )
.抽签法 .随机数法
.分层随机抽样 .其他抽样方法
【答案】:
小试牛刀
例1:某学校有在职人员160人,其中行政人员有16人,教师有112人,后勤人员有32人.教育部门为了了解在职人员对学校机构改革的意见,要从中抽取一个容量为20的样本,请利用分层随机抽样的方法抽取,并写出抽样过程.
解:第一步:确定抽样比,样本容量与总体容量的比为,
第二步:确定分别从三类人员中抽取的人数,
从行政人员中抽取(人),
从教师中抽取(人),
从后勤人员中抽取(人);
第三步:用简单随机抽样方法抽取行政、教师、后勤人员为2人,14人,4人.
第四步,把抽取的个体组合在一起构成所需样本.
小试牛刀
练习:为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~ 70岁,40~ 50岁,20~ 30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽取了30人进行调查,若在60~ 70岁这个年龄段中抽查了8人,则x为( ).
A.90 B.120 C.180 D.200
小试牛刀
练习:为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~ 70岁,40~ 50岁,20~ 30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽取了30人进行调查,若在60~ 70岁这个年龄段中抽查了8人,则x为( ).
A.90 B.120 C.180 D.200
小试牛刀
解:从60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中抽取30人,每个个体被抽到的概率为,
∵在60~70岁这个年龄段中抽查了8人,∴,解得x=200.
新知探究
问3:在简单随机抽样中如何估计总体平均数?
用样本平均数估计总体平均数
追问:那么在分层随机抽样中,还能用样本平均数估计总体平均数吗?
在分层随机抽样中,如果层数分别为2层,
第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n.
第1层总体的各个个体的变量值为:X1,X2,…,XM;
第1层样本的各个个体的变量值为:x1,x2,…,xm;
第2层总体的各个个体的变量值为:Y1,Y2,…,YN;
第2层样本的各个个体的变量值为:y1,y2,…,yn.
新知探究
总体平均数 样本平均数
第1层
第2层
总体
可得
在比例分配的分层随机抽样中
我们可以直接用样本平均数估计总体平均数
例2:将一个总体分为A,B,C三层,其个体数之比依次为5∶3∶2.若用分层随机抽样方法抽取容量为100的样本,则A,B,C三层的样本的平均数分别为15,30,20.
(1)求样本的平均数; (2)估计总体平均数.
解析:(1)样本平均数. (2)总体平均数约为20.5.
新知探究
1、高二年级有男生490人,女生510人,张华按男、女生进行分层,通过分层随机抽样的方法,得到男生、女生的平均身高分别为170.2cm和160.8 cm.
(1)如果张华在各层中按比例分配样本,总样本量为100,那么在男生、女生中分别抽取了多少名 在这种情况下,请估计高二年级全体学生的平均身高.
(2)如果张华从男生、女生中抽取的样本量分别为30和70,那么在这种情况下,如何估计高二年级全体学生的平均身高更合理
教材P184
小试牛刀
解:(1)男生应抽取人,女生应抽取人,
∴样本平均数为.
(2)应按(1)的方法进行改进更合理,即高二年级全体学生的平均身高估计为:
.
小试牛刀
证明:
课后思考
可以直接用样本平均数估计总体平均值
课堂小结
9.1.2分层随机抽样
学习目标
通过实例了解分层随机抽样的概念、特点和操作步骤
01
掌握各层样本量化比例分配的方法
02
03
掌握分层抽样中样本平均数与总体平均数的计算方法
1. 简单随机抽样的概念:
简单随机抽样的特点:
2. 简单随机抽样的常用方法:
③机会均等.
①总体有限个;
②逐个抽取;
①抽签法;
②随机数表法
设一个总体含有有限个个体,并记其个体数为N.如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的机会相等,就称这样的抽样为简单随机抽样.
3. 总体均值与样本均值
用样本的平均数估计总体的平均数
新知探究
新知探究
问1:在高一年级的712名学生中,男生有326名, 女生有386名,现要了解全体高一年级学生的平均身高,要从中抽取一个容量为50的样本.
追问:会不会出现“极端样本”,50个个体大部分来自高个子或矮个子的 情形?
新知探究
问2:是否对男生、女生分别进行简单随机抽样?
追问:如何抽才能更加准确?
为了使样本的结构与总体的分布相近,人数多的群体应多抽一些,人数少的群体应少抽一些.
即可按男生、女生在全体学生中所占的比例进行分配:
新知探究
男生样本量=
男生人数
全体学生数
×总样本量
女生样本量=
女生人数
全体学生数
×总样本量
无论男生、女生,每个学生被抽到的概率都相等.
均为
分层随机抽样的定义:
一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样,每一个子总体称为层.
在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.
新知探究
分层随机抽样的步骤:
分层
按某种特征将总体分成若干部分(层)
计算
抽样比
抽样比
定数
按抽样比确定每层抽取的个体数=每层数量×
抽样
各层分别按简单随机抽样的方法抽取样本
汇总
综合各层抽样,组成样本
新知探究
练习:某中学有老年教师20人,中年教师65人,青年教师95人,为了调查他们的健康状况,需从他们中抽取一个样本容量为36的样本,则合适的抽样方法是( )
.抽签法 .随机数法
.分层随机抽样 .其他抽样方法
【答案】:
小试牛刀
例1:某学校有在职人员160人,其中行政人员有16人,教师有112人,后勤人员有32人.教育部门为了了解在职人员对学校机构改革的意见,要从中抽取一个容量为20的样本,请利用分层随机抽样的方法抽取,并写出抽样过程.
解:第一步:确定抽样比,样本容量与总体容量的比为,
第二步:确定分别从三类人员中抽取的人数,
从行政人员中抽取(人),
从教师中抽取(人),
从后勤人员中抽取(人);
第三步:用简单随机抽样方法抽取行政、教师、后勤人员为2人,14人,4人.
第四步,把抽取的个体组合在一起构成所需样本.
小试牛刀
练习:为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~ 70岁,40~ 50岁,20~ 30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽取了30人进行调查,若在60~ 70岁这个年龄段中抽查了8人,则x为( ).
A.90 B.120 C.180 D.200
小试牛刀
练习:为了了解某社区居民有无收看“奥运会开幕式”的情况,某记者分别从该社区60~ 70岁,40~ 50岁,20~ 30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽取了30人进行调查,若在60~ 70岁这个年龄段中抽查了8人,则x为( ).
A.90 B.120 C.180 D.200
小试牛刀
解:从60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中抽取30人,每个个体被抽到的概率为,
∵在60~70岁这个年龄段中抽查了8人,∴,解得x=200.
新知探究
问3:在简单随机抽样中如何估计总体平均数?
用样本平均数估计总体平均数
追问:那么在分层随机抽样中,还能用样本平均数估计总体平均数吗?
在分层随机抽样中,如果层数分别为2层,
第1层和第2层包含的个体数分别为M和N,抽取的样本量分别为m和n.
第1层总体的各个个体的变量值为:X1,X2,…,XM;
第1层样本的各个个体的变量值为:x1,x2,…,xm;
第2层总体的各个个体的变量值为:Y1,Y2,…,YN;
第2层样本的各个个体的变量值为:y1,y2,…,yn.
新知探究
总体平均数 样本平均数
第1层
第2层
总体
可得
在比例分配的分层随机抽样中
我们可以直接用样本平均数估计总体平均数
例2:将一个总体分为A,B,C三层,其个体数之比依次为5∶3∶2.若用分层随机抽样方法抽取容量为100的样本,则A,B,C三层的样本的平均数分别为15,30,20.
(1)求样本的平均数; (2)估计总体平均数.
解析:(1)样本平均数. (2)总体平均数约为20.5.
新知探究
1、高二年级有男生490人,女生510人,张华按男、女生进行分层,通过分层随机抽样的方法,得到男生、女生的平均身高分别为170.2cm和160.8 cm.
(1)如果张华在各层中按比例分配样本,总样本量为100,那么在男生、女生中分别抽取了多少名 在这种情况下,请估计高二年级全体学生的平均身高.
(2)如果张华从男生、女生中抽取的样本量分别为30和70,那么在这种情况下,如何估计高二年级全体学生的平均身高更合理
教材P184
小试牛刀
解:(1)男生应抽取人,女生应抽取人,
∴样本平均数为.
(2)应按(1)的方法进行改进更合理,即高二年级全体学生的平均身高估计为:
.
小试牛刀
证明:
课后思考
可以直接用样本平均数估计总体平均值
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
