2.9有理数的乘方课件(北京课改版七年级上)
文档属性
| 名称 | 2.9有理数的乘方课件(北京课改版七年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 75.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 20:45:00 | ||
图片预览







文档简介
课件24张PPT。课 题
§2.9 有理数的乘方(一)教学目标: 1. 经历探索乘方意义的过程,在现实背 景中了解乘方的意义;3. 能根据有理数乘方的意义进行有理数的乘方运算;4. 培养学生的观察、比较、分析、归纳、概括能力,以及学生的探索精神.2. 能结合具体表达式正确的读、写及指出底数、指数、幂的意义;重点: 有理数的乘方的意义难点: 1. 有理数的乘方的意义的探索过程
2.通过自主探索有理数乘方的意义,初
步学习把生活实际和数学知识联系起来
的学习方法,深刻认识知识的合理性3.在个人独立的积极思考和亲自实际操作中学习数学.想一想: 在你的生活中是否遇到过这样的问题――根据问题列出的算式是2个、3个或3个以上的相同数的连乘积形式?
1个细胞,每过1小时可以分裂为2个同样的细胞,那么2小时后这个细胞可以繁殖成多少个同样的细胞? 3小时呢? 5小时呢? 式子表示: 2×2 2×2×2 2×2×2×2×2 (1)生物学问题:(2)“一尺之棰,日取其半,万世
而不竭”,那么10天之后,这个
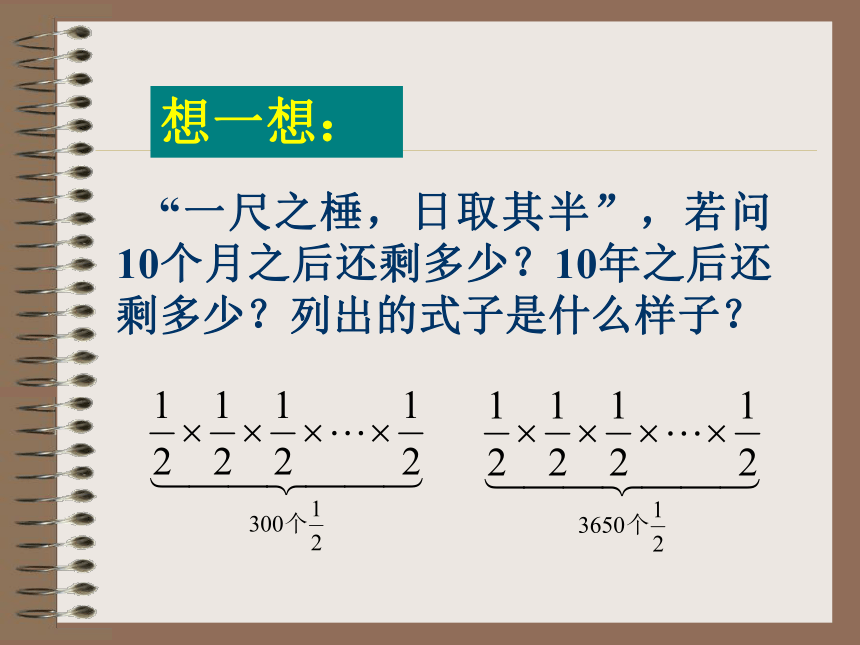
“一尺之棰”还剩多少?式子表示: 想一想: “一尺之棰,日取其半”,若问10个月之后还剩多少?10年之后还剩多少?列出的式子是什么样子?
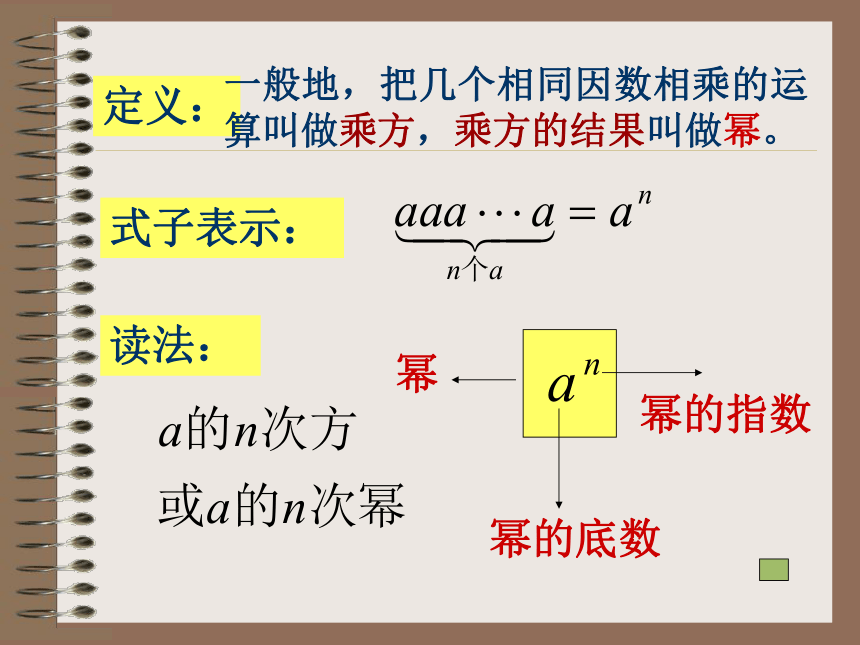
出现问题: 当相同因数相乘而因数的个数非常多时,造成乘法的算式和算法的重复和繁锁,需要创造一种简单的表达方式:写成 写成 写成 写成 定义: 一般地,把几个相同因数相乘的运算叫做乘方,乘方的结果叫做幂。 式子表示: 读法: 强 调: (1) 可以看做 的一次幂,
即 的指数是1;( 2)练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是
数,读作 ;
4)在 中,底数是 ;指数是 ;读作 ;
底指-3的16次方17 的17次方5)5看成幂的话,底数是 ,指数是 ,可读作 ;
6) 看成幂的话,底数是 ,指数是 ,可读作 ; 515 的一次方1的一次方练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;注意问题: 负数和分数写成乘方形式时,
须加括号.
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ; 对错错错例1:说出下列各式的读法、意义、
底数和指数,并计算:
(1)(2) (3) (4) (5) 例2:利用计算器计算:(1) (2) (1)乘方是特殊的乘法运算,特殊在于所
乘的因数是相同的;(2)乘法由于相同因数的增加而质变为乘方.课后小结1.有理数乘方的意义、读法、各部分的
名称及注意的问题;2.乘方和乘法的联系: 我们知道,一张报纸大约
只有 厘米厚,如果把这张
报纸连续对折30次后,它的厚
度会达到多少?
补充内容:(厚度达到107200米,比世界第一高峰---珠穆朗玛峰的高度8848米还高) 棋盘上的学问
在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人——宰相西萨·班·达依尔。国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3个小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧!”国王觉得这个要求太容易满足了,就命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始记数时,国王才发现:就是把全印度甚至全世界的麦粒都拿来,也满足不了那位宰相的要求。那么宰相要求得到的麦粒到底有多少呢? 用计算器不难求得其总数是
18446744073709551615(粒)
?
谢谢!
§2.9 有理数的乘方(一)教学目标: 1. 经历探索乘方意义的过程,在现实背 景中了解乘方的意义;3. 能根据有理数乘方的意义进行有理数的乘方运算;4. 培养学生的观察、比较、分析、归纳、概括能力,以及学生的探索精神.2. 能结合具体表达式正确的读、写及指出底数、指数、幂的意义;重点: 有理数的乘方的意义难点: 1. 有理数的乘方的意义的探索过程
2.通过自主探索有理数乘方的意义,初
步学习把生活实际和数学知识联系起来
的学习方法,深刻认识知识的合理性3.在个人独立的积极思考和亲自实际操作中学习数学.想一想: 在你的生活中是否遇到过这样的问题――根据问题列出的算式是2个、3个或3个以上的相同数的连乘积形式?
1个细胞,每过1小时可以分裂为2个同样的细胞,那么2小时后这个细胞可以繁殖成多少个同样的细胞? 3小时呢? 5小时呢? 式子表示: 2×2 2×2×2 2×2×2×2×2 (1)生物学问题:(2)“一尺之棰,日取其半,万世
而不竭”,那么10天之后,这个
“一尺之棰”还剩多少?式子表示: 想一想: “一尺之棰,日取其半”,若问10个月之后还剩多少?10年之后还剩多少?列出的式子是什么样子?
出现问题: 当相同因数相乘而因数的个数非常多时,造成乘法的算式和算法的重复和繁锁,需要创造一种简单的表达方式:写成 写成 写成 写成 定义: 一般地,把几个相同因数相乘的运算叫做乘方,乘方的结果叫做幂。 式子表示: 读法: 强 调: (1) 可以看做 的一次幂,
即 的指数是1;( 2)练习一
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7的7次方底指12的10次方 3)在 中,-3是 数,16是
数,读作 ;
4)在 中,底数是 ;指数是 ;读作 ;
底指-3的16次方17 的17次方5)5看成幂的话,底数是 ,指数是 ,可读作 ;
6) 看成幂的话,底数是 ,指数是 ,可读作 ; 515 的一次方1的一次方练习二
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3)= ;
4、 = ;注意问题: 负数和分数写成乘方形式时,
须加括号.
二、把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = ;
思考:用乘方式子怎么表示 的相反数?练习三
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ; 对错错错例1:说出下列各式的读法、意义、
底数和指数,并计算:
(1)(2) (3) (4) (5) 例2:利用计算器计算:(1) (2) (1)乘方是特殊的乘法运算,特殊在于所
乘的因数是相同的;(2)乘法由于相同因数的增加而质变为乘方.课后小结1.有理数乘方的意义、读法、各部分的
名称及注意的问题;2.乘方和乘法的联系: 我们知道,一张报纸大约
只有 厘米厚,如果把这张
报纸连续对折30次后,它的厚
度会达到多少?
补充内容:(厚度达到107200米,比世界第一高峰---珠穆朗玛峰的高度8848米还高) 棋盘上的学问
在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人——宰相西萨·班·达依尔。国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3个小格给4粒,以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧!”国王觉得这个要求太容易满足了,就命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始记数时,国王才发现:就是把全印度甚至全世界的麦粒都拿来,也满足不了那位宰相的要求。那么宰相要求得到的麦粒到底有多少呢? 用计算器不难求得其总数是
18446744073709551615(粒)
?
谢谢!
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
