4.3图形的相似 讲义（教师版）

中小学教育资源及组卷应用平台
第01讲 相似三角形的判定定理
一、判定三角形相似的三种定理
定义法：三边成比例的两个三角形相似.（第一种）
定理 1：两角分别相等的两个三角形相似.（第二种）
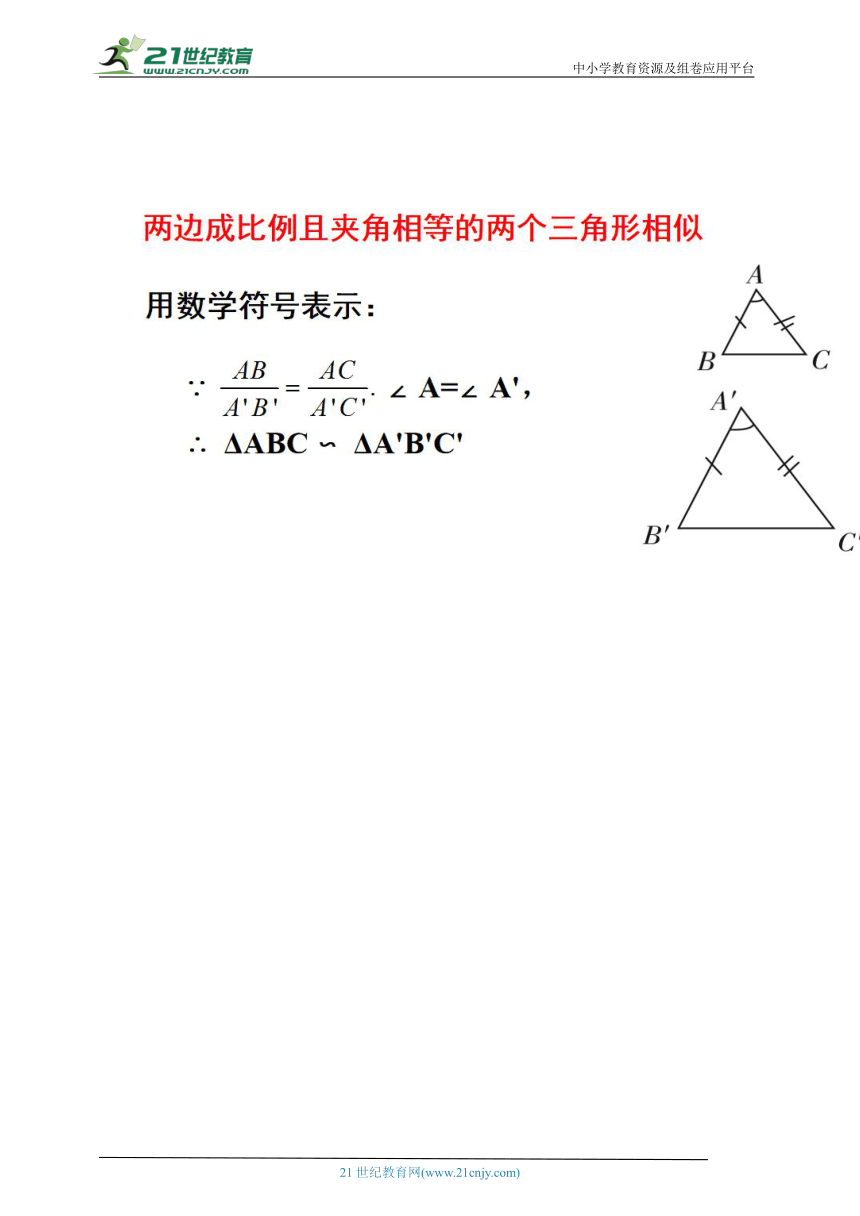
定理 2：两边成比例且夹角相等的两个三角形相似.（第三种）
强化练习
一．选择题
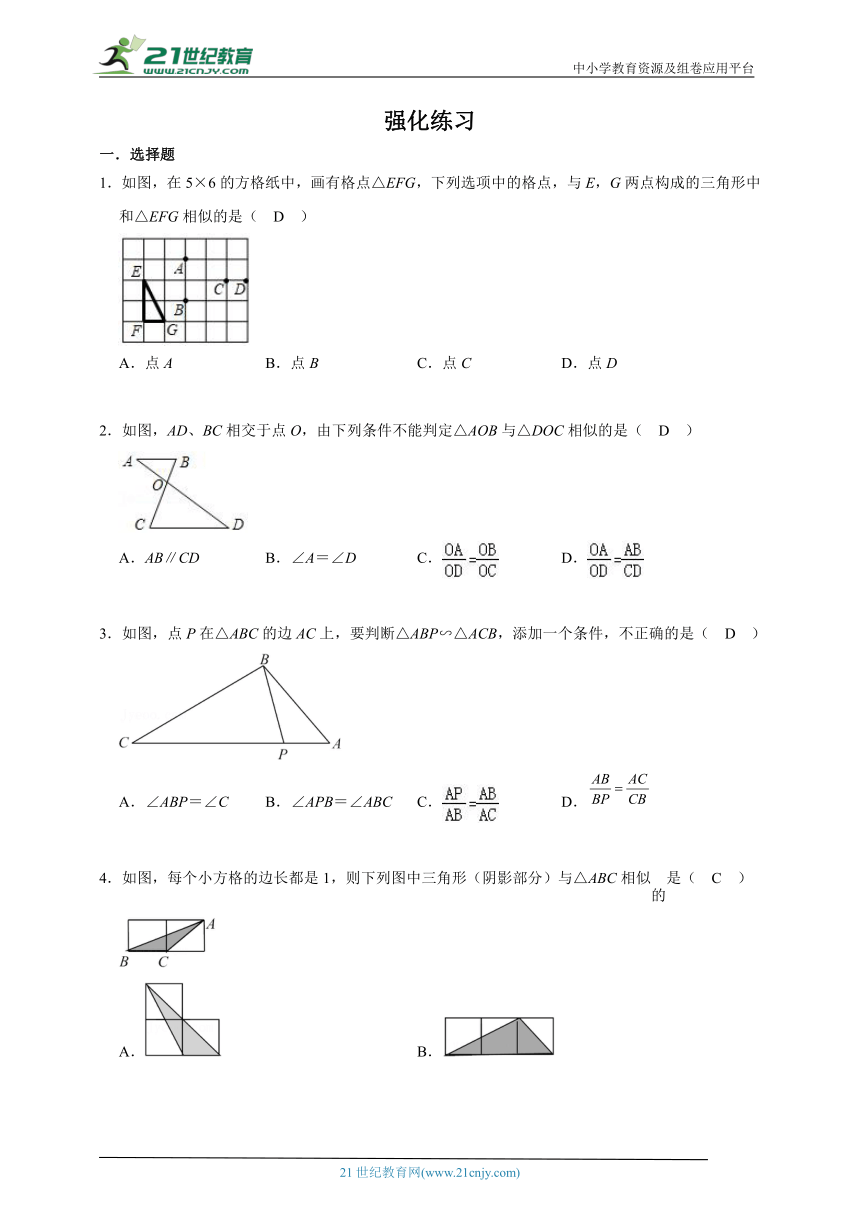
1．如图，在5×6的方格纸中，画有格点△EFG，下列选项中的格点，与E，G两点构成的三角形中和△EFG相似的是（　D　）
A．点A B．点B C．点C D．点D
2．如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是（　D　）
A．AB∥CD B．∠A＝∠D C． D．
3．如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　D　）
A．∠ABP＝∠C B．∠APB＝∠ABC C． D．
4．如图，每个小方格的边长都是1，则下列图中三角形（阴影部分）与△ABC相似的是（　C　）
A． B．
C． D．
5．如图，在钝角三角形ABC中，AB＝6cm，AC＝12cm，动点D从点A出发沿AB以1cm/s的速度向点B运动，同时动点E从点C出发沿CA以2cm/s的速度向点A运动，当以A，D，E为顶点的三角形与△ABC相似时，运动时间是（　A　）
A．3s或4.8s B．3s C．4.5s D．4.5s或4.8s
6．如图，D，E分别是△ABC的边AB，AC上的点，添加下列条件仍不能判定△ADE与△ABC相似（　D　）
A．DE∥BC B．∠ADE＝∠ACB C． D．
7.下列各组条件中，一定能够判定△ABC与△DEF相似的是（ C　）
A．∠A＝∠B，∠D＝∠E
B．∠B＝∠E，AB＝3，AC＝4，DE：DF＝3：4
C．△ABC三边长分别为6，18，21，△DEF三边之比为2：7：6
D．∠C＝91°，∠E＝91°，DE：AB＝EF：AC
8．如图，M为线段AB上一点，AD与BC交于E，∠CMD＝∠A＝∠B，BC交MD于F，AD交MC于G，则图中相似三角形有（　B　）
A．4对 B．3对 C．2对 D．1对
9．如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（　D　）
A．∠B＝∠D B． C．∠C＝∠AED D．
10．将两个完全相同的等腰直角△ABC与△AFG按图所示的方式放置，那么图中一定相似（不含全等）的三角形是（　B　）
A．△AEC与△ADB B．△ABE与△DAE C．△ABC与△ADE D．△AEC与△ADC
三、图形的位似
1、位似多边形的定义：如果两个相似多边形任意一组对应点P,P’所在的直线都经过同一个点O，
且有OP′=k·OP （k≠0），那么这样的两个多边形叫做位似多边形，点O 叫做位似中心。
其中k等于相似多边形的相似比.
5.位似中心的位置由两个图形的位置决定，可能在
两个图形的同侧，异侧，图形的内部，边上，或顶点上
平面直角坐标系中的位似变换
在平面直角坐标系中，将一个多边形每个顶点的横、纵坐标都乘以同一个数k（k≠0），所对应的图形与原图形位似，位似中心是坐标原点，他们的相似比为∣k∣.
例1. 如图，△ABO缩小后变为△A′B′O，其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上．若线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为（　　）
A．（，n） B．（m，n） C．（m，） D．（）
【解析】根据A，B两点坐标以及对应点A′，B′点的坐标得出坐标变化规律，进而得出P′的坐标．
解：∵△ABO缩小后变为△A′B′O，其中A、B的对应点分别为A′、B′，点A、B、A′、B′均在图中在格点上，
即A点坐标为：（4，6），B点坐标为：（6，2），A′点坐标为：（2，3），B′点坐标为：（3，1），
∴线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为：（）．
故选D．
例2. 已知两点A（5，6）、B（7，2），先将线段AB向左平移一个单位，再以原点O为位似中心，在第一象限内将其缩小为原来的得到线段CD，则点A的对应点C的坐标为（　　）
A．（2，3） B．（3，1） C．（2，1） D．（3，3）
【解析】先根据点平移的规律得到A点平移后的对应点的坐标为（4，6），然后根据在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k求解．
解：∵线段AB向左平移一个单位，
∴A点平移后的对应点的坐标为（4，6），
∴点C的坐标为（4×，6×），即（2，3）．
例3.在直角坐标系中，△OAB三个顶点的坐标分别为O（0,0），A（3,0），B（2,3）.
（1）将点O，A，B的横、纵坐标都乘以2，得到三个点O′，A′，B′，请你在坐标系中找到这三个点。
（2）以这三个点为顶点的三角形与△OAB位似吗？为什么？如果位似，指出位似中心和相似比。
强化练习
1．如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（3，4），点C（2，2），点D（3，1），则点D的对应点B的坐标是（　C　）
A．（4，2） B．（4，1） C．（5，2） D．（5，1）
2．如图，以点O为位似中心，将△ABC放大得到△DEF．若AD=OA，则△ABC与△DEF的面积之比为（B　）
A．1：2 B．1：4 C．1：5 D．1：6
3．在平面直角坐标系中，已知点A（﹣4，2），B（﹣6，﹣4），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（　D　）
A．（﹣2，1） B．（﹣8，4） C．（﹣8，4）或（8，﹣4） D．（﹣2，1）或（2，﹣1）
4． 如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD．
若B（1，0），则点C的坐标为（　B　）
A．（1，2） B．（1，1） C．（，） D．（2，1）
5．如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象你限内将线段AB缩小为原来的后得到线段CD，则端点C和D的坐标分别为（C　）
（2，2），（3，2） B．（2，4），（3，1） C．（2，2），（3，1） D．（3，1），（2，2）
6．如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P 为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（　C　）
A．（0，0） B．（0，1） C．（﹣3，2） D．（3，﹣2）
7．（2015 武汉）如图，在直角坐标系中，有两点A（6，3），B（6，0），以原点O位似中心，相似比为，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（　A　）
A．（2，1） B．（2，0） C．（3，3） D．（3，1）
8．下列关于位似图形的表述：
①相似图形一定是位似图形，位似图形一定是相似图形；
②位似图形一定有位似中心；
③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形 是位似 图形；
④位似图形上任意两点与位似中心的距离之比等于位似比．
其中正确命题的序号是（A　）
A．②③ B．①② C．③④ D．②③④
9．如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′ 与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，=k．已知关于x，y的二元一次方程（m，n是实数）无解，在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则k t的值等于（　D　）
B．1 C． D．
10．如图，△ABC与△DEF位似，位似中心为点O，且△ABC的面积等于△DEF面积的，则AB：DE= 　2:3 ．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)