13.1三角形课件(北京课改版八年级上)
文档属性
| 名称 | 13.1三角形课件(北京课改版八年级上) |  | |
| 格式 | rar | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 20:45:00 | ||
图片预览






文档简介
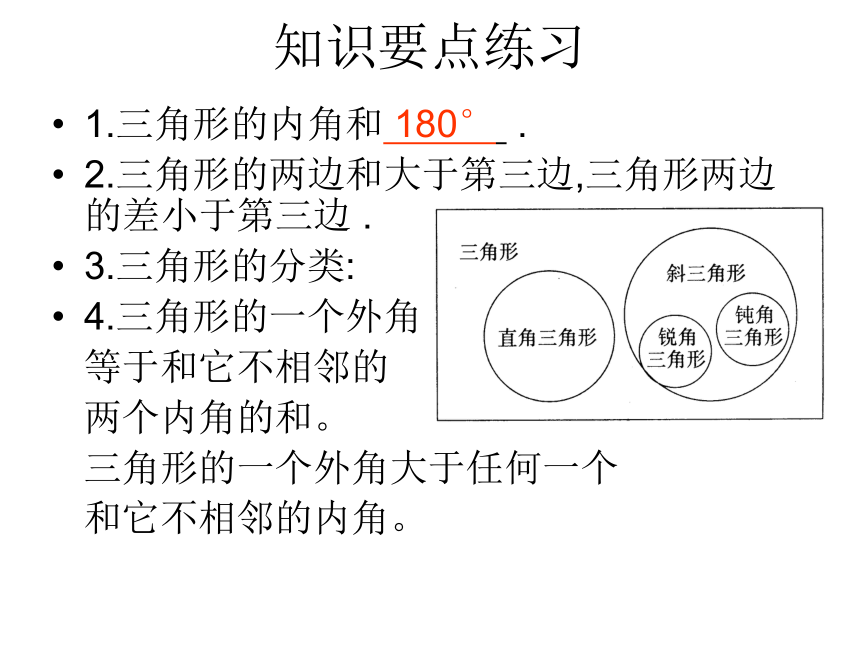
课件24张PPT。13.1三角形知识要点练习1.三角形的内角和 180° .
2.三角形的两边和大于第三边,三角形两边的差小于第三边 .
3.三角形的分类:
4.三角形的一个外角
等于和它不相邻的
两个内角的和。
三角形的一个外角大于任何一个
和它不相邻的内角。例1、已知:∠CAE是三角形ABC的外角, ∠1=∠2,AD∥BC 。求证:AB=AC例2.若a,b,c是三角形的三边长, 则代数式a2-2ab-c2+b2的值是( )
A.大于0 B.等于0
C.小于0 D不能确定C全等三角形能够完全重合的两个三角形叫全等三角形
全等用符号“≌”表示
全等三角形的对应边相等;
对应角相等。.全等三角形的判定
1、边角边公理:有两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”)
注意:一定要是两边夹角,而不能是边边角。
2、角边角公理:有两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角“或“ASA”)
3、推论有两角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边’域“AAS”)
4、边边边公理有三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”)
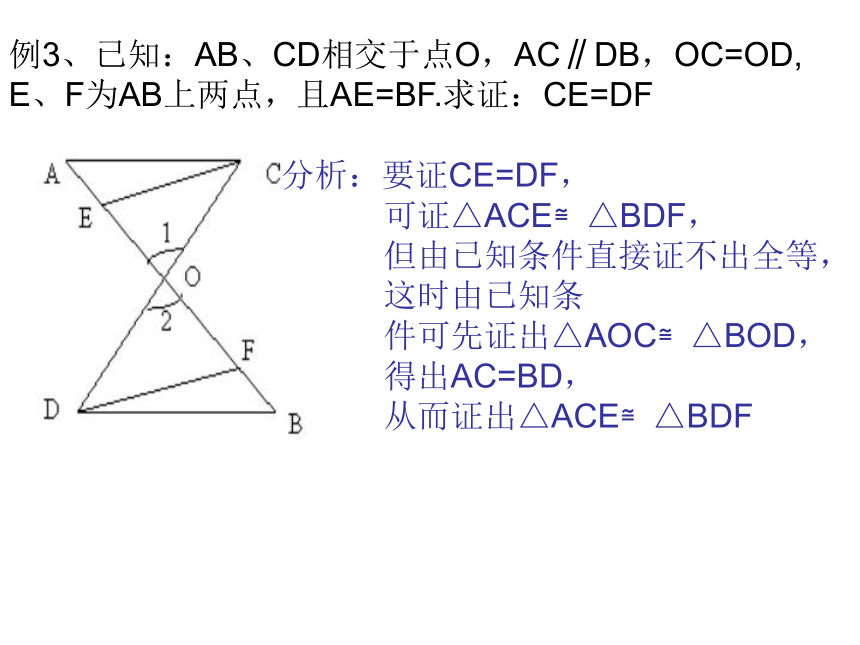
5、直角三角形全等的判定:斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边,直角边”或“HL”例3、已知:AB、CD相交于点O,AC∥DB,OC=OD,
E、F为AB上两点,且AE=BF.求证:CE=DF分析:要证CE=DF,
可证△ACE≌△BDF,
但由已知条件直接证不出全等,
这时由已知条
件可先证出△AOC≌△BOD,
得出AC=BD,
从而证出△ACE≌△BDF 1.如图:已知△ABC中,AD⊥BC于D, ∠DAC=∠DCA,CE⊥AB于E,交AD于F,求证:AB=CF2.在四边形ABCD中,E是AC上一点, ∠1=∠2, ∠3= ∠4,求证: ∠5= ∠6.C等腰三角形等腰三角形的性质定理:等腰三角形的两个底角相等(简写成“等边对等角”)
推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,就是说:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。(三线合一)
推论2:等边三角形的各角都相等,并且每一个角都等于60°
等腰三角形的判定定理:如果一个三角形有两个角相,那这两个角所对的两条边也相等。(简写成“等角对等边”)。
推论1:三个角都相等的三角形是等边三角形
推论2:有一个角等于60°的等腰三角形是等边三角形
推论3:在直角三角形中,如果一个锐角等于3O°,那么它所对的直角边等于斜边的一半。角平分线 定理1、在角的平分线上的点到这个角的两边的距离相等。
定理2、一个角的两边的距离相等的点,在这个角的平分线上。定理:线段垂直平分线上的点和这条线段两个端点的距离相等
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线例4、已知:如图 ,OE平分∠AOB,
EC⊥OA于 C,ED⊥OB于 D.
求证:(1)OC=OD;
(2)OE垂直平分CD. 例5.在△ABC中,AB=AC, ∠A=36°BD,CE是角平分线.图中等腰三角形有几个?ABCDEF勾股定理勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方:
勾股定理的逆定理:如果三角形的三边长a、b、c有下面关系:
那么这个三角形是直角三角形解直角三角形 一、锐角三角函数:在直角三角形ABC中,∠C是直角.
1、正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
2、余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
3、正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
4、余切:把锐角A的邻边与对边的比叫做∠A的余切,记作tanA·cotA=l 0< sinA< l; 0<cosA<;l sinA=cos(90°一 A)=cosB;
cosA=sin(90°一A)=sinBtanA=cot(90°一 A)=cotB;
cotA=tan(90°-A)= tanB 90°一A = B 一些特殊角0.30.45.60.90的三角函数值 (3)(2)∠A十∠B=90°;;; 例如一杆AB直立地面,从D点看杆顶A,仰角为60°,
从C点看杆顶A,仰角为30°(如图5~2)
若CD长为10米,求杆AB的高。相似三角形1、相似三角形:两个角对应相等,边对应成比例的三角形叫做相似三角形。
2、相似比:相似三角形对应边的比k,叫做相似比(或叫做相似系数)。
3、相似三角形的基本定理:平分于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 三角形相似的判定定理
(1)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么就两个三角形相似。可简单说成:两角对应相等,两三角形相似。
(2)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,可简单说成:两边对应成比例且夹角相等,两三角形相似。
(3)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简单说成:三边对应成比例,两三角形相似。
(4)直角三角形相似的判定定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。如图,已知,AD为△ABC的角平分线,AE=DE,求证:DE2=BE﹡CE 相似三角形的性质
(1)相似三角形性质1:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
(2)相似三角形性质2:相似三角形周长的比等于相似比。
说明:以上两个性质简单记为:相似三角形对应线段的比等于相似比。
(3)相似三角形面积的比等于相似比的平方。
说明:两个三角形相似,根据定义可知它们具有对应角相等、对应边成比例这个性质。如图,AD:AB=1:3,DE//BC,则△ADE和△ABC的面积比为多少?如果△ABC的面积为9那么四边的积是多少?第一:顶角(或底角)相等的两个等腰三角形相似。
第二:腰和底对应成比例的两个等腰三角形相似。
第三:有一个锐角相等的两个直角三角形相似。
第四:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
第五:如果一个三角形的两边和其中一边上的中线与另一个三角形的两边和其中一边上的中线对应成比例,那么这两个三角形相似 如图:△ABC中, ∠ACB=90°,CD⊥AB于D,DE⊥AC于E.
求证:
2.三角形的两边和大于第三边,三角形两边的差小于第三边 .
3.三角形的分类:
4.三角形的一个外角
等于和它不相邻的
两个内角的和。
三角形的一个外角大于任何一个
和它不相邻的内角。例1、已知:∠CAE是三角形ABC的外角, ∠1=∠2,AD∥BC 。求证:AB=AC例2.若a,b,c是三角形的三边长, 则代数式a2-2ab-c2+b2的值是( )
A.大于0 B.等于0
C.小于0 D不能确定C全等三角形能够完全重合的两个三角形叫全等三角形
全等用符号“≌”表示
全等三角形的对应边相等;
对应角相等。.全等三角形的判定
1、边角边公理:有两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”)
注意:一定要是两边夹角,而不能是边边角。
2、角边角公理:有两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角“或“ASA”)
3、推论有两角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边’域“AAS”)
4、边边边公理有三边对应相等的两个三角形全等(可以简写成“边边边”或“SSS”)
5、直角三角形全等的判定:斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边,直角边”或“HL”例3、已知:AB、CD相交于点O,AC∥DB,OC=OD,
E、F为AB上两点,且AE=BF.求证:CE=DF分析:要证CE=DF,
可证△ACE≌△BDF,
但由已知条件直接证不出全等,
这时由已知条
件可先证出△AOC≌△BOD,
得出AC=BD,
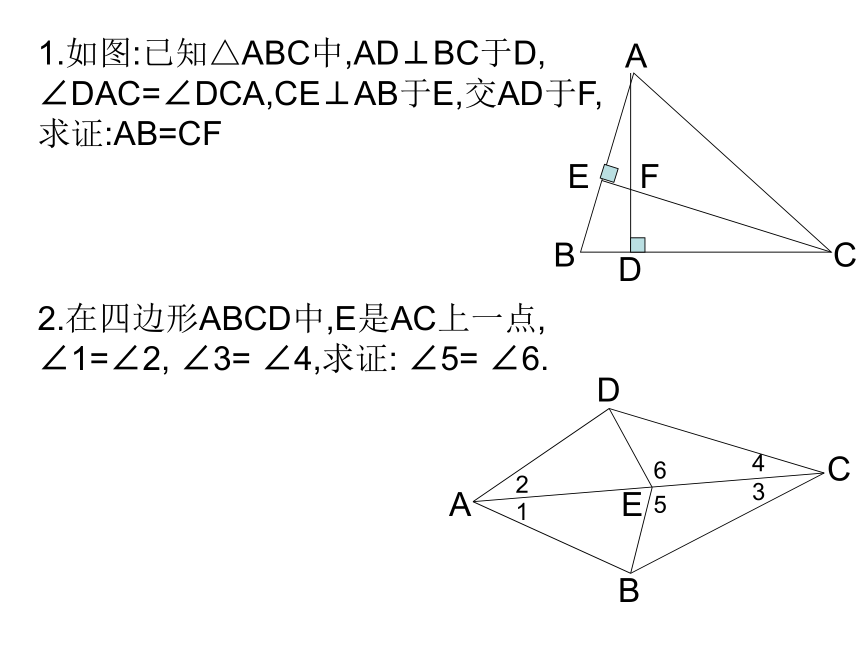
从而证出△ACE≌△BDF 1.如图:已知△ABC中,AD⊥BC于D, ∠DAC=∠DCA,CE⊥AB于E,交AD于F,求证:AB=CF2.在四边形ABCD中,E是AC上一点, ∠1=∠2, ∠3= ∠4,求证: ∠5= ∠6.C等腰三角形等腰三角形的性质定理:等腰三角形的两个底角相等(简写成“等边对等角”)
推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,就是说:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。(三线合一)
推论2:等边三角形的各角都相等,并且每一个角都等于60°
等腰三角形的判定定理:如果一个三角形有两个角相,那这两个角所对的两条边也相等。(简写成“等角对等边”)。
推论1:三个角都相等的三角形是等边三角形
推论2:有一个角等于60°的等腰三角形是等边三角形
推论3:在直角三角形中,如果一个锐角等于3O°,那么它所对的直角边等于斜边的一半。角平分线 定理1、在角的平分线上的点到这个角的两边的距离相等。
定理2、一个角的两边的距离相等的点,在这个角的平分线上。定理:线段垂直平分线上的点和这条线段两个端点的距离相等
逆定理:和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线例4、已知:如图 ,OE平分∠AOB,
EC⊥OA于 C,ED⊥OB于 D.
求证:(1)OC=OD;
(2)OE垂直平分CD. 例5.在△ABC中,AB=AC, ∠A=36°BD,CE是角平分线.图中等腰三角形有几个?ABCDEF勾股定理勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方:
勾股定理的逆定理:如果三角形的三边长a、b、c有下面关系:
那么这个三角形是直角三角形解直角三角形 一、锐角三角函数:在直角三角形ABC中,∠C是直角.
1、正弦:把锐角A的对边与斜边的比叫做∠A的正弦,记作
2、余弦:把锐角A的邻边与斜边的比叫做∠A的余弦,记作
3、正切:把锐角A的对边与邻边的比叫做∠A的正切,记作
4、余切:把锐角A的邻边与对边的比叫做∠A的余切,记作tanA·cotA=l 0< sinA< l; 0<cosA<;l sinA=cos(90°一 A)=cosB;
cosA=sin(90°一A)=sinBtanA=cot(90°一 A)=cotB;
cotA=tan(90°-A)= tanB 90°一A = B 一些特殊角0.30.45.60.90的三角函数值 (3)(2)∠A十∠B=90°;;; 例如一杆AB直立地面,从D点看杆顶A,仰角为60°,
从C点看杆顶A,仰角为30°(如图5~2)
若CD长为10米,求杆AB的高。相似三角形1、相似三角形:两个角对应相等,边对应成比例的三角形叫做相似三角形。
2、相似比:相似三角形对应边的比k,叫做相似比(或叫做相似系数)。
3、相似三角形的基本定理:平分于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。 三角形相似的判定定理
(1)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么就两个三角形相似。可简单说成:两角对应相等,两三角形相似。
(2)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似,可简单说成:两边对应成比例且夹角相等,两三角形相似。
(3)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简单说成:三边对应成比例,两三角形相似。
(4)直角三角形相似的判定定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。如图,已知,AD为△ABC的角平分线,AE=DE,求证:DE2=BE﹡CE 相似三角形的性质
(1)相似三角形性质1:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比。
(2)相似三角形性质2:相似三角形周长的比等于相似比。
说明:以上两个性质简单记为:相似三角形对应线段的比等于相似比。
(3)相似三角形面积的比等于相似比的平方。
说明:两个三角形相似,根据定义可知它们具有对应角相等、对应边成比例这个性质。如图,AD:AB=1:3,DE//BC,则△ADE和△ABC的面积比为多少?如果△ABC的面积为9那么四边的积是多少?第一:顶角(或底角)相等的两个等腰三角形相似。
第二:腰和底对应成比例的两个等腰三角形相似。
第三:有一个锐角相等的两个直角三角形相似。
第四:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
第五:如果一个三角形的两边和其中一边上的中线与另一个三角形的两边和其中一边上的中线对应成比例,那么这两个三角形相似 如图:△ABC中, ∠ACB=90°,CD⊥AB于D,DE⊥AC于E.
求证:
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
