沪科版九年级数学上册试题 第23章《解直角三角形》章节测试卷(含解析)
文档属性
| 名称 | 沪科版九年级数学上册试题 第23章《解直角三角形》章节测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 811.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 00:00:00 | ||
图片预览



文档简介
第23章《解直角三角形》章节测试卷
一.选择题(共9小题,满分27分,每小题3分)
1.在中,、都是锐角,且,,则是( ).
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
2.直角三角形纸片,两直角边,,现将纸片按如图那样折叠,使A与电B重合,折痕为,则的值是( )
A. B. C.1 D.
3.如图,的顶点分别在单位长度为1的正方形网格的格点上,则的值为( )
A. B. C. D.
4.如图,在中,,点D、E分别在上,交于F,若,,则的值为( )
A. B. C. D.
5.一块直角三角板按如图放置,顶点的坐标为,直角顶点的坐标为,,则点的坐标为( )
B.
C. D.
6.在中,,有一个锐角为60°,,若点P在直线上(不与点A、C重合),且,则的长为( )
A.6或 B.6或 C.或 D.6或或
7.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
8.如图,在△ABC中,,分别以AB,AC,BC为边向外作正方形,连结CD,若,则tan∠CDB的值为( )
A. B. C. D.
9.如图1是由四个全等的直角三角形组成的“风车”图案,其中,延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若,则该“风车”的面积为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
10.如图,在中,,点,分别在,边上,且,,连接,,交于点,,,则的长为 .
11.如图,在菱形中,,于点,的延长线与的延长线交于点,则 .(表示面积)
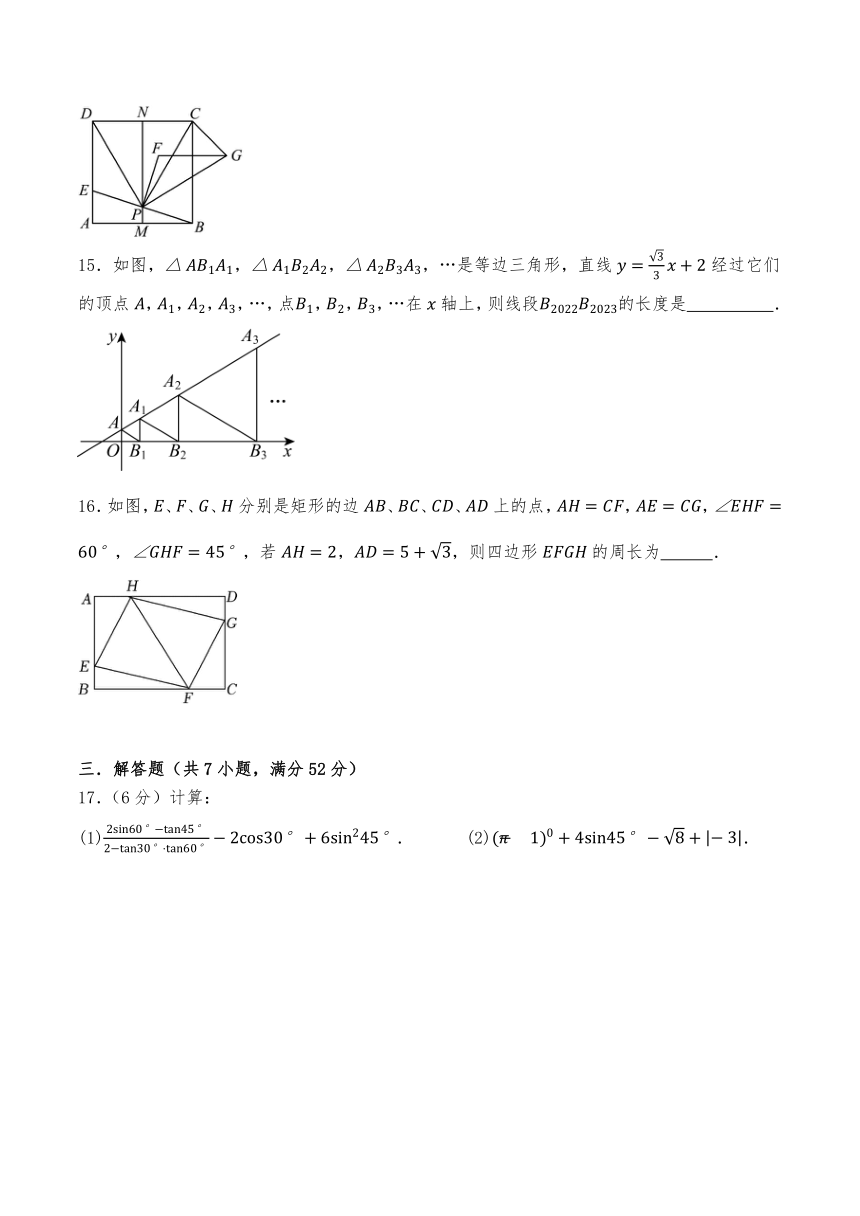
12.如图,在矩形中,,是对角线上一动点(点不与点,重合),当是等腰三角形时, .
13.如图,已知点P是菱形的对角线延长线上一点,过点P分别作,延长线的垂线,垂足分别为点E,F.若,,则的值为 .
14.如图,在正方形中,,分别是,的中点,是线段上的一点,的延长线交于点,连接,,将绕点顺时针旋转得,则下列结论:,;垂直平分;若,点在边上运动,则,两点之间距离的最小值是.其中结论正确的序号有 .
15.如图,,,,…是等边三角形,直线经过它们的顶点,,,,…,点,,,…在轴上,则线段的长度是 .
16.如图,、、、分别是矩形的边、、、上的点,,,,,若,,则四边形的周长为 .
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1). (2).
18.(6分)如图,在中,于点D,若,,.
求:
(1)的长;
(2)的值.
19.(8分)(2023春·河南南阳·九年级统考期中)如图,已知点A(7,8)、C(0,6),AB⊥x轴,垂足为点B,点D在线段OB上,DE∥AC,交AB于点E,EF∥CD,交AC于点F.
(1)求经过A、C两点的直线的表达式;
(2)设OD=t,BE=s,求s与t的函数关系式;
(3)是否存在点D,使四边形CDEF为矩形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
20.(8分)(1)在如图1的正方形网格图中,每个小正方形的边长为1,A,B,C,D均为格点(小正方形的顶点). 求证:.
(2)在如图2所示的正方形网格图中,每个小正方形的边长为1,A,B,C均为格点,请你仅用无刻度的直尺在线段AC上求作一点P, 使得∠PBA=∠C,并简要说明理由.
21.(9分)如图,小明为测量宣传牌的高度,他站在距离建筑楼底部处6米远的地面处,测得宣传牌的底部的仰角为.同时测得建筑楼窗户处的仰角为(在同一直线上.)然后,小明沿坡度为的斜坡从走到处,此时正好与地面平行,小明在处又测得宣传牌顶部的仰角为.
(1)填空:__________度,__________度;
(2)求距离地面的高度(结果保留根号);
(3)求宣传牌的高度(结果保留根号).
22.(9分)我们定义:等腰三角形中底边与腰的比叫做顶角正对(),如图①,在中,,顶角A的正对记作,这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)________.
(2)对于,的正对值的取值范围是________.
(3)如图②,已知,其中为锐角,试求的值.
23.(9分)已知:中,,D为直线上一点.
(1)如图1,于点H,若,求证:.
(2)如图2,,点D在延长线上,点E在上且,若,,求的值.
(3)如图3,D在延长线上,E为上一点,且满足:,,若,,求的长.
答案解析
一.选择题
1.B
【分析】根据特殊角的三角函数值求出,然后利用三角形内角和定理求出的度数,即可解答.
【详解】解:∵,,
∴,
∴,
∴是等边三角形,
故选:B.
2.B
【分析】根据折叠的性质得出,设,则,在中,根据勾股定理得出,列出方程求出x的值,最后根据正切的定义,即可解答.
【详解】解:∵沿折叠得到,
∴,
设,则,
在中,根据勾股定理可得:,
即,解得:,
∴,
故选:B.
3.B
【分析】过B作于点D,根据勾股定理得出的值,再利用面积公式求出的值,由可得角的正弦值.
【详解】解:如图,过B作于点D
根据勾股定理得:
∴
∴
∴
故选:B.
4.C
【分析】如图,过作,交的延长线于,证明,则,证明,则,解得,,根据,计算求解即可.
【详解】解:如图,过作,交的延长线于,
∴,
在和中,
∵,
∴,
∴,
∵,,
∴,
∴,解得,
∴,
∴,
故选:C.
5.D
【分析】过点作于点,根据为直角三角形可证明,求出,求出,再由比例线段可求出,长,则答案可求出.
【详解】解:过点作于点,
为直角三角形,
,
,
,
在中,,
在中,,
,
,
,
解得,,
,
点的坐标为,.
故选:D.
6.D
【分析】根据点P在直线上的不同位置,,利用特殊角的三角函数进行求解.
【详解】如图1:
当时,,与矛盾;
如图2:
当时,,
∵,
∴,
∴是等边三角形,
∴;
如图3:
当时,,
∵,
∴,
∴,
∵,
∴,
∴
如图4:
当时,,
∵,
∴,
∴
故选:D
7.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
8.D
【分析】过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,可得△ABC,△BED,△BEC,△BCF都是直角三角形,根据sin∠BCE=,设BE=3a,BC=5 a,得CE==4 a,过点C作DB延长线于点G,得矩形CFBG,设AC=x,AB=y,然后利用勾股定理和三角形的面积可得=,进而利用锐角三角函数即可解决问题.
【详解】解:如图,过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,
∴△ABC,△BED,△BEC,△BCF都是直角三角形,
∵sin∠BCD=,
∴sin∠BCE=,
设BE=3a,BC=5a,
∴CE==4a,
过点C作DB延长线于点G,得矩形CFBG,
∴BF=CG,
设AC=x,AB=y,
在Rt△ABC中,根据勾股定理,得
AB2﹣AC2=BC2,
∴y2﹣x2=25a2,
∵S△ABC=AB CF=AC BC,
∴y CF=5ax,
∴CF=,
在Rt△BCF中,根据勾股定理,得
BF===,
∴BF=CG=,
在正方形ABDH中,AB=BD=y,
在Rt△BDE中,根据勾股定理,得
DE==,
∴CD=CE+ED=4a +,
∵S△CBD=CD BE=BD CG,
∴CD BE=BD CG,
∴(4a +)×3=y×,
∴=,
∴tan∠CDB=tan∠EDB===.
故选:D.
9.B
【分析】连接AC,由题意可得Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH,进而说明△OAC为等腰直角三角形,再说明分CD、GI垂直平分AB,进而说明∠OBH=∠OHB=45°,然后再运用解直角三角形求得AI,然后再求得三角形AOB的面积,最后求风车面积即可.
【详解】解:如图:连接AC
由题意可得:Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH
∴OA=OC, ∠OAB= ∠OCD
∵∠AOC=∠AOB=90°
∴△OAC为等腰直角三角形
又∵∠OAB= ∠OCD:
∴∠AJD=180°-∠ADJ-∠OAB
=180°-∠ODC-∠OCD=90°,即AJ⊥CD
又∵CJ=DJ
∴AJ垂直平分CD
同理:GI垂直平分AB
∴AC=AD,AJ是等腰三角形顶角∠CAD的角平分线
即∠DAJ=∠CAD=×45°=22.5°
易得IH=BJ,IJ=IB+BJ=IB+IH
又∵IB=IA
∴IJ=IB+BJ=IH+IA=
在Rt△ABO中,∠ABH=∠BAH=22.5°
∴∠OBH=OHB=45°
设OB=OH=a,即AH=BH=OB=a
∴tan∠A=
∴
设IH=()x,AI=x
∴IH+IA==,即x=1
∴
又∵
∴
∴
∴.
故选B.
二.填空题
10.
【分析】过点作,交于点,连接,勾股定理求得,过点作,证明重合,进而勾股定理即可求解.
【详解】解:如图所示,过点作,交于点,连接,
则四边形是平行四边形,
∴,
∵,则
∴
∴是直角三角形,
∴
∵
∴
∵
∴
∵
过点作,
∵
∴,
∴重合,
∴
故答案为:.
11.
【分析】设,则,根据勾股定理求出,然后证明,最后根据相似三角形的性质求解即可.
【详解】解∶ ∵,,
∴,
设,则,
∴,
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴.
故答案为:.
12.2或或
【分析】分三种情况,分别画出图形,即可求解.
【详解】解:在矩形中,,
∴,
∴,
当时,过点作于点,
则,
∴,
∴
∴,
当时,,
当时,过点作于点,
∴,,
∴,
∴,
综上所述 或或,
故答案为:或或.
13.
【分析】如图,延长交于,由菱形的性质可知,为,的平分线,则,,由题意知,为底边上的高,由菱形,,,可得,根据,计算求解,进而可得结果.
【详解】解:如图,延长交于,
由菱形的性质可知,为,的平分线,
∵,,
∴,
∴,
由题意知,为底边上的高,
∵菱形,,,
∴,
∴,
∴,
故答案为:.
14.
【分析】延长交于点,连接,,,由已知可得为,的垂直平分线,由垂直平分线的性质和图形旋转的性质可得的结论正确;利用三角形的内角和定理和等腰三角形的性质计算可得,由四边形内角和定理通过计算可得;利用平行线的性质可得,则,可说明的结论正确;通过证明点,,,在以点为圆心,为半径的同一个圆上,利用圆周角定理可得,得到,,三点共线,得到为等腰直角三角形,则的结论正确;由题意点在对角线上运动,当时,的值最小,连接,解直角三角形的知识可得的结论不正确.
【详解】解:延长交于点,连接,,,如图,
正方形中,,分别是,的中点,
是线段,的垂直平分线.
,.
是绕点顺时针旋转得到,
≌,
.
.
的结论正确;
,
.
,
.
.
,
.
,
.
≌,
.
,
.
,
.
,
.
即.
,
.
.
.
的结论正确;
,,
,
,
,.
.
.
,
.
点,,,在以点为圆心,为半径的同一个圆上.
.
点在对角线上,
.
,
为等腰直角三角形.
平分,
垂直平分.
的结论正确;
由以上可知:点在正方形的对角线上运动,
当时,的值最小.
此时点与点重合,
.
的结论不正确.
综上,结论正确的序号有:,
故答案为:.
15.
【分析】设直线与轴交于点,求出点、的坐标,可得,推出,,然后求出,,,…,进而可得,,再求出即可.
【详解】解:如图所示,设直线与轴交于点,
当时,;当时,,
,,
,,
,
,
是等边三角形,
,
,,
,
,
,
,
同理,,,……,
,,
,
故答案为:.
16.
【分析】先构造 的直角三角形,求得 的余弦和正切值;作,可求得;作,分别交直线于和,构造“一线三等角”,先求得的长,进而根据相似三角形求得,进而求得,于是得出,进一步求得结果.
【详解】解:如图1,
中,,,,
设,则,,,
,,
如图2,
作于,作,分别交直线于和,
四边形是矩形,
,
在与中,
,
,
,
同理证得,则,
四边形是平行四边形,
设,则,,
,
,
,
,
可得:,,,
,
,
,
,
,
,
,
,
,
,
,
,
四边形的周长为:,
故答案为:.
三.解答题
17.(1)原式
.
(2)原式
.
18.(1)解:∵,
∴,
在中,,,
∴;
(2)解:由(2)得,
∴,
∴,
在中,,即.
19.解:(1)设直线AC的表达式为y=kx+b
将点A、C的坐标代入,得
得:,
解得:,
故直线AC的表达式为:y=x+6;
(2)∵OD=t,BE=s,AB⊥x轴
∴则点D(t,0),点E(7,s)
∵DE∥AC
可设直线DE的解析式为y=x+c
将点D的坐标代入
0=t+c
解得:c=﹣t
∴直线的表达式为:y=x﹣t,
将点E的坐标代入,得s=2﹣t(根据点D在线段OB上,可得0<t<7);
(3)存在,理由:
设点D(t,0),由(2)BE=2﹣t,
四边形CDEF为矩形,则∠CDE=90°,
∵∠EDB+∠CDO=90°,∠CDO+∠OCD=90°,
∴∠OCD=∠BDE,
∴tan∠OCD=tan∠BDE,
∴=
即=,
解得:t=或7(因为0<t<7,故舍去7),
故点D的坐标为(,0).
20.(1)如图所示,取格点E,F,连接,,
∵,,
∴,
∵,,
∴,
∴,
∴;
(2)解:如图,取格点D,E,
同理(1)可得,在中,,
在中,,
∴,
∴,
直线与的交点为所求的点P.
21.(1)解:由题意,得,
∴
∴,
由题意,得,
∴
∴.
(2)解:如图,过点作于,
由题意得,,
∴四边形是矩形.
.
在中,(米),
(米).
答:距离地面的高度为米;
(3)解:∵斜坡的坡度为,
中,(米),
(米).
∴在中,,
米.
在中,(米),
(米).
答:宣传牌的高度约为米.
22.(1)解:如图,,
,
∵,
∴.
(2)解:如图,点A在的中垂线上,当点A向靠近时,增大,逐渐接近,腰长接近, 相应的;
当点A远离时,减小,逐渐接近,腰长逐渐增大,相应的逐渐接近0,;
∴
(3)解:如图,在上截取,过H作于D,
,
设,则,,
∴.
中,,
∴.
23.(1)解:证明:如图1,
过点作于,
,
,
,
,
在和中,
,
,
,
,
;
(2)如图2,在上取一点,使,连接,
,
,
,
,
,
,
,即,
,
设,则,
,,
,
,
,
;
(3)如图3,过点作于,作交的延长线于,
设,,则,
,
,
,,
,,
,
,即,
,
,
,
,
,
.
一.选择题(共9小题,满分27分,每小题3分)
1.在中,、都是锐角,且,,则是( ).
A.等腰三角形 B.等边三角形 C.直角三角形 D.钝角三角形
2.直角三角形纸片,两直角边,,现将纸片按如图那样折叠,使A与电B重合,折痕为,则的值是( )
A. B. C.1 D.
3.如图,的顶点分别在单位长度为1的正方形网格的格点上,则的值为( )
A. B. C. D.
4.如图,在中,,点D、E分别在上,交于F,若,,则的值为( )
A. B. C. D.
5.一块直角三角板按如图放置,顶点的坐标为,直角顶点的坐标为,,则点的坐标为( )
B.
C. D.
6.在中,,有一个锐角为60°,,若点P在直线上(不与点A、C重合),且,则的长为( )
A.6或 B.6或 C.或 D.6或或
7.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
8.如图,在△ABC中,,分别以AB,AC,BC为边向外作正方形,连结CD,若,则tan∠CDB的值为( )
A. B. C. D.
9.如图1是由四个全等的直角三角形组成的“风车”图案,其中,延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若,则该“风车”的面积为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
10.如图,在中,,点,分别在,边上,且,,连接,,交于点,,,则的长为 .
11.如图,在菱形中,,于点,的延长线与的延长线交于点,则 .(表示面积)
12.如图,在矩形中,,是对角线上一动点(点不与点,重合),当是等腰三角形时, .
13.如图,已知点P是菱形的对角线延长线上一点,过点P分别作,延长线的垂线,垂足分别为点E,F.若,,则的值为 .
14.如图,在正方形中,,分别是,的中点,是线段上的一点,的延长线交于点,连接,,将绕点顺时针旋转得,则下列结论:,;垂直平分;若,点在边上运动,则,两点之间距离的最小值是.其中结论正确的序号有 .
15.如图,,,,…是等边三角形,直线经过它们的顶点,,,,…,点,,,…在轴上,则线段的长度是 .
16.如图,、、、分别是矩形的边、、、上的点,,,,,若,,则四边形的周长为 .
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1). (2).
18.(6分)如图,在中,于点D,若,,.
求:
(1)的长;
(2)的值.
19.(8分)(2023春·河南南阳·九年级统考期中)如图,已知点A(7,8)、C(0,6),AB⊥x轴,垂足为点B,点D在线段OB上,DE∥AC,交AB于点E,EF∥CD,交AC于点F.
(1)求经过A、C两点的直线的表达式;
(2)设OD=t,BE=s,求s与t的函数关系式;
(3)是否存在点D,使四边形CDEF为矩形?若存在,请直接写出点D的坐标;若不存在,请说明理由.
20.(8分)(1)在如图1的正方形网格图中,每个小正方形的边长为1,A,B,C,D均为格点(小正方形的顶点). 求证:.
(2)在如图2所示的正方形网格图中,每个小正方形的边长为1,A,B,C均为格点,请你仅用无刻度的直尺在线段AC上求作一点P, 使得∠PBA=∠C,并简要说明理由.
21.(9分)如图,小明为测量宣传牌的高度,他站在距离建筑楼底部处6米远的地面处,测得宣传牌的底部的仰角为.同时测得建筑楼窗户处的仰角为(在同一直线上.)然后,小明沿坡度为的斜坡从走到处,此时正好与地面平行,小明在处又测得宣传牌顶部的仰角为.
(1)填空:__________度,__________度;
(2)求距离地面的高度(结果保留根号);
(3)求宣传牌的高度(结果保留根号).
22.(9分)我们定义:等腰三角形中底边与腰的比叫做顶角正对(),如图①,在中,,顶角A的正对记作,这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)________.
(2)对于,的正对值的取值范围是________.
(3)如图②,已知,其中为锐角,试求的值.
23.(9分)已知:中,,D为直线上一点.
(1)如图1,于点H,若,求证:.
(2)如图2,,点D在延长线上,点E在上且,若,,求的值.
(3)如图3,D在延长线上,E为上一点,且满足:,,若,,求的长.
答案解析
一.选择题
1.B
【分析】根据特殊角的三角函数值求出,然后利用三角形内角和定理求出的度数,即可解答.
【详解】解:∵,,
∴,
∴,
∴是等边三角形,
故选:B.
2.B
【分析】根据折叠的性质得出,设,则,在中,根据勾股定理得出,列出方程求出x的值,最后根据正切的定义,即可解答.
【详解】解:∵沿折叠得到,
∴,
设,则,
在中,根据勾股定理可得:,
即,解得:,
∴,
故选:B.
3.B
【分析】过B作于点D,根据勾股定理得出的值,再利用面积公式求出的值,由可得角的正弦值.
【详解】解:如图,过B作于点D
根据勾股定理得:
∴
∴
∴
故选:B.
4.C
【分析】如图,过作,交的延长线于,证明,则,证明,则,解得,,根据,计算求解即可.
【详解】解:如图,过作,交的延长线于,
∴,
在和中,
∵,
∴,
∴,
∵,,
∴,
∴,解得,
∴,
∴,
故选:C.
5.D
【分析】过点作于点,根据为直角三角形可证明,求出,求出,再由比例线段可求出,长,则答案可求出.
【详解】解:过点作于点,
为直角三角形,
,
,
,
在中,,
在中,,
,
,
,
解得,,
,
点的坐标为,.
故选:D.
6.D
【分析】根据点P在直线上的不同位置,,利用特殊角的三角函数进行求解.
【详解】如图1:
当时,,与矛盾;
如图2:
当时,,
∵,
∴,
∴是等边三角形,
∴;
如图3:
当时,,
∵,
∴,
∴,
∵,
∴,
∴
如图4:
当时,,
∵,
∴,
∴
故选:D
7.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
8.D
【分析】过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,可得△ABC,△BED,△BEC,△BCF都是直角三角形,根据sin∠BCE=,设BE=3a,BC=5 a,得CE==4 a,过点C作DB延长线于点G,得矩形CFBG,设AC=x,AB=y,然后利用勾股定理和三角形的面积可得=,进而利用锐角三角函数即可解决问题.
【详解】解:如图,过点B作BE⊥CD于点E,过点C作CF⊥AB于点F,
∴△ABC,△BED,△BEC,△BCF都是直角三角形,
∵sin∠BCD=,
∴sin∠BCE=,
设BE=3a,BC=5a,
∴CE==4a,
过点C作DB延长线于点G,得矩形CFBG,
∴BF=CG,
设AC=x,AB=y,
在Rt△ABC中,根据勾股定理,得
AB2﹣AC2=BC2,
∴y2﹣x2=25a2,
∵S△ABC=AB CF=AC BC,
∴y CF=5ax,
∴CF=,
在Rt△BCF中,根据勾股定理,得
BF===,
∴BF=CG=,
在正方形ABDH中,AB=BD=y,
在Rt△BDE中,根据勾股定理,得
DE==,
∴CD=CE+ED=4a +,
∵S△CBD=CD BE=BD CG,
∴CD BE=BD CG,
∴(4a +)×3=y×,
∴=,
∴tan∠CDB=tan∠EDB===.
故选:D.
9.B
【分析】连接AC,由题意可得Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH,进而说明△OAC为等腰直角三角形,再说明分CD、GI垂直平分AB,进而说明∠OBH=∠OHB=45°,然后再运用解直角三角形求得AI,然后再求得三角形AOB的面积,最后求风车面积即可.
【详解】解:如图:连接AC
由题意可得:Rt△AOB≌Rt△DCO≌Rt△EOF≌Rt△GOH
∴OA=OC, ∠OAB= ∠OCD
∵∠AOC=∠AOB=90°
∴△OAC为等腰直角三角形
又∵∠OAB= ∠OCD:
∴∠AJD=180°-∠ADJ-∠OAB
=180°-∠ODC-∠OCD=90°,即AJ⊥CD
又∵CJ=DJ
∴AJ垂直平分CD
同理:GI垂直平分AB
∴AC=AD,AJ是等腰三角形顶角∠CAD的角平分线
即∠DAJ=∠CAD=×45°=22.5°
易得IH=BJ,IJ=IB+BJ=IB+IH
又∵IB=IA
∴IJ=IB+BJ=IH+IA=
在Rt△ABO中,∠ABH=∠BAH=22.5°
∴∠OBH=OHB=45°
设OB=OH=a,即AH=BH=OB=a
∴tan∠A=
∴
设IH=()x,AI=x
∴IH+IA==,即x=1
∴
又∵
∴
∴
∴.
故选B.
二.填空题
10.
【分析】过点作,交于点,连接,勾股定理求得,过点作,证明重合,进而勾股定理即可求解.
【详解】解:如图所示,过点作,交于点,连接,
则四边形是平行四边形,
∴,
∵,则
∴
∴是直角三角形,
∴
∵
∴
∵
∴
∵
过点作,
∵
∴,
∴重合,
∴
故答案为:.
11.
【分析】设,则,根据勾股定理求出,然后证明,最后根据相似三角形的性质求解即可.
【详解】解∶ ∵,,
∴,
设,则,
∴,
∵四边形是菱形,
∴,,
∴,
∵,
∴,
∴,
∴.
故答案为:.
12.2或或
【分析】分三种情况,分别画出图形,即可求解.
【详解】解:在矩形中,,
∴,
∴,
当时,过点作于点,
则,
∴,
∴
∴,
当时,,
当时,过点作于点,
∴,,
∴,
∴,
综上所述 或或,
故答案为:或或.
13.
【分析】如图,延长交于,由菱形的性质可知,为,的平分线,则,,由题意知,为底边上的高,由菱形,,,可得,根据,计算求解,进而可得结果.
【详解】解:如图,延长交于,
由菱形的性质可知,为,的平分线,
∵,,
∴,
∴,
由题意知,为底边上的高,
∵菱形,,,
∴,
∴,
∴,
故答案为:.
14.
【分析】延长交于点,连接,,,由已知可得为,的垂直平分线,由垂直平分线的性质和图形旋转的性质可得的结论正确;利用三角形的内角和定理和等腰三角形的性质计算可得,由四边形内角和定理通过计算可得;利用平行线的性质可得,则,可说明的结论正确;通过证明点,,,在以点为圆心,为半径的同一个圆上,利用圆周角定理可得,得到,,三点共线,得到为等腰直角三角形,则的结论正确;由题意点在对角线上运动,当时,的值最小,连接,解直角三角形的知识可得的结论不正确.
【详解】解:延长交于点,连接,,,如图,
正方形中,,分别是,的中点,
是线段,的垂直平分线.
,.
是绕点顺时针旋转得到,
≌,
.
.
的结论正确;
,
.
,
.
.
,
.
,
.
≌,
.
,
.
,
.
,
.
即.
,
.
.
.
的结论正确;
,,
,
,
,.
.
.
,
.
点,,,在以点为圆心,为半径的同一个圆上.
.
点在对角线上,
.
,
为等腰直角三角形.
平分,
垂直平分.
的结论正确;
由以上可知:点在正方形的对角线上运动,
当时,的值最小.
此时点与点重合,
.
的结论不正确.
综上,结论正确的序号有:,
故答案为:.
15.
【分析】设直线与轴交于点,求出点、的坐标,可得,推出,,然后求出,,,…,进而可得,,再求出即可.
【详解】解:如图所示,设直线与轴交于点,
当时,;当时,,
,,
,,
,
,
是等边三角形,
,
,,
,
,
,
,
同理,,,……,
,,
,
故答案为:.
16.
【分析】先构造 的直角三角形,求得 的余弦和正切值;作,可求得;作,分别交直线于和,构造“一线三等角”,先求得的长,进而根据相似三角形求得,进而求得,于是得出,进一步求得结果.
【详解】解:如图1,
中,,,,
设,则,,,
,,
如图2,
作于,作,分别交直线于和,
四边形是矩形,
,
在与中,
,
,
,
同理证得,则,
四边形是平行四边形,
设,则,,
,
,
,
,
可得:,,,
,
,
,
,
,
,
,
,
,
,
,
,
四边形的周长为:,
故答案为:.
三.解答题
17.(1)原式
.
(2)原式
.
18.(1)解:∵,
∴,
在中,,,
∴;
(2)解:由(2)得,
∴,
∴,
在中,,即.
19.解:(1)设直线AC的表达式为y=kx+b
将点A、C的坐标代入,得
得:,
解得:,
故直线AC的表达式为:y=x+6;
(2)∵OD=t,BE=s,AB⊥x轴
∴则点D(t,0),点E(7,s)
∵DE∥AC
可设直线DE的解析式为y=x+c
将点D的坐标代入
0=t+c
解得:c=﹣t
∴直线的表达式为:y=x﹣t,
将点E的坐标代入,得s=2﹣t(根据点D在线段OB上,可得0<t<7);
(3)存在,理由:
设点D(t,0),由(2)BE=2﹣t,
四边形CDEF为矩形,则∠CDE=90°,
∵∠EDB+∠CDO=90°,∠CDO+∠OCD=90°,
∴∠OCD=∠BDE,
∴tan∠OCD=tan∠BDE,
∴=
即=,
解得:t=或7(因为0<t<7,故舍去7),
故点D的坐标为(,0).
20.(1)如图所示,取格点E,F,连接,,
∵,,
∴,
∵,,
∴,
∴,
∴;
(2)解:如图,取格点D,E,
同理(1)可得,在中,,
在中,,
∴,
∴,
直线与的交点为所求的点P.
21.(1)解:由题意,得,
∴
∴,
由题意,得,
∴
∴.
(2)解:如图,过点作于,
由题意得,,
∴四边形是矩形.
.
在中,(米),
(米).
答:距离地面的高度为米;
(3)解:∵斜坡的坡度为,
中,(米),
(米).
∴在中,,
米.
在中,(米),
(米).
答:宣传牌的高度约为米.
22.(1)解:如图,,
,
∵,
∴.
(2)解:如图,点A在的中垂线上,当点A向靠近时,增大,逐渐接近,腰长接近, 相应的;
当点A远离时,减小,逐渐接近,腰长逐渐增大,相应的逐渐接近0,;
∴
(3)解:如图,在上截取,过H作于D,
,
设,则,,
∴.
中,,
∴.
23.(1)解:证明:如图1,
过点作于,
,
,
,
,
在和中,
,
,
,
,
;
(2)如图2,在上取一点,使,连接,
,
,
,
,
,
,
,即,
,
设,则,
,,
,
,
,
;
(3)如图3,过点作于,作交的延长线于,
设,,则,
,
,
,,
,,
,
,即,
,
,
,
,
,
.
