沪科版九年级数学下册试题第 25章《投影与视图》章节测试卷(含解析)
文档属性
| 名称 | 沪科版九年级数学下册试题第 25章《投影与视图》章节测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-18 11:45:16 | ||
图片预览


文档简介
第25章《投影与视图》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
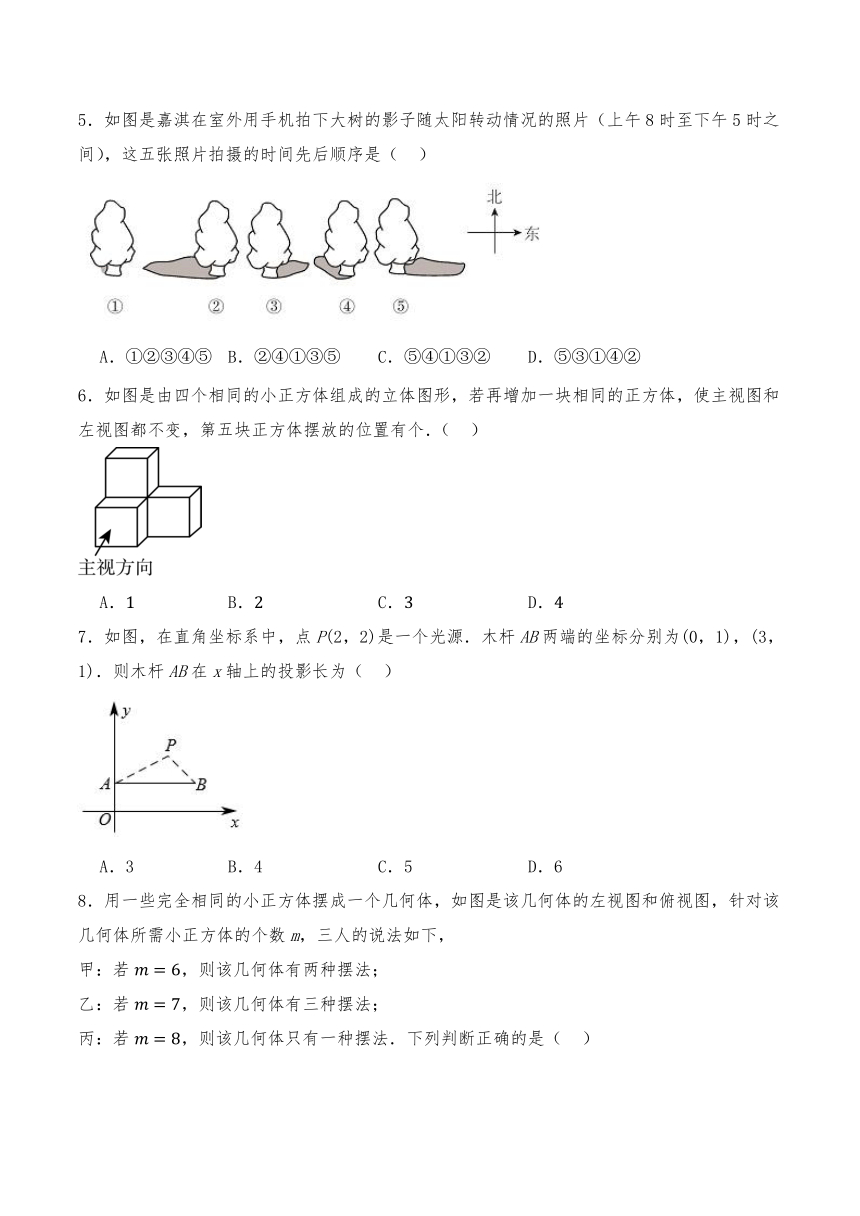
1.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A. B.
C. D.
2.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A.5 B.6 C.7 D.8
3.下列关于投影的说法正确的是( )
A.平行投影中的光线是聚成一点的
B.线段的正投影还是线段
C.圆形物体在阳光下的投影可能是椭圆
D.若两人在路灯下的影子一样长,则两人身高也相同
4.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径,扇形的圆心角等于,则围成的圆锥的母线长R的值为( )
A.2 B.4 C.8 D.10
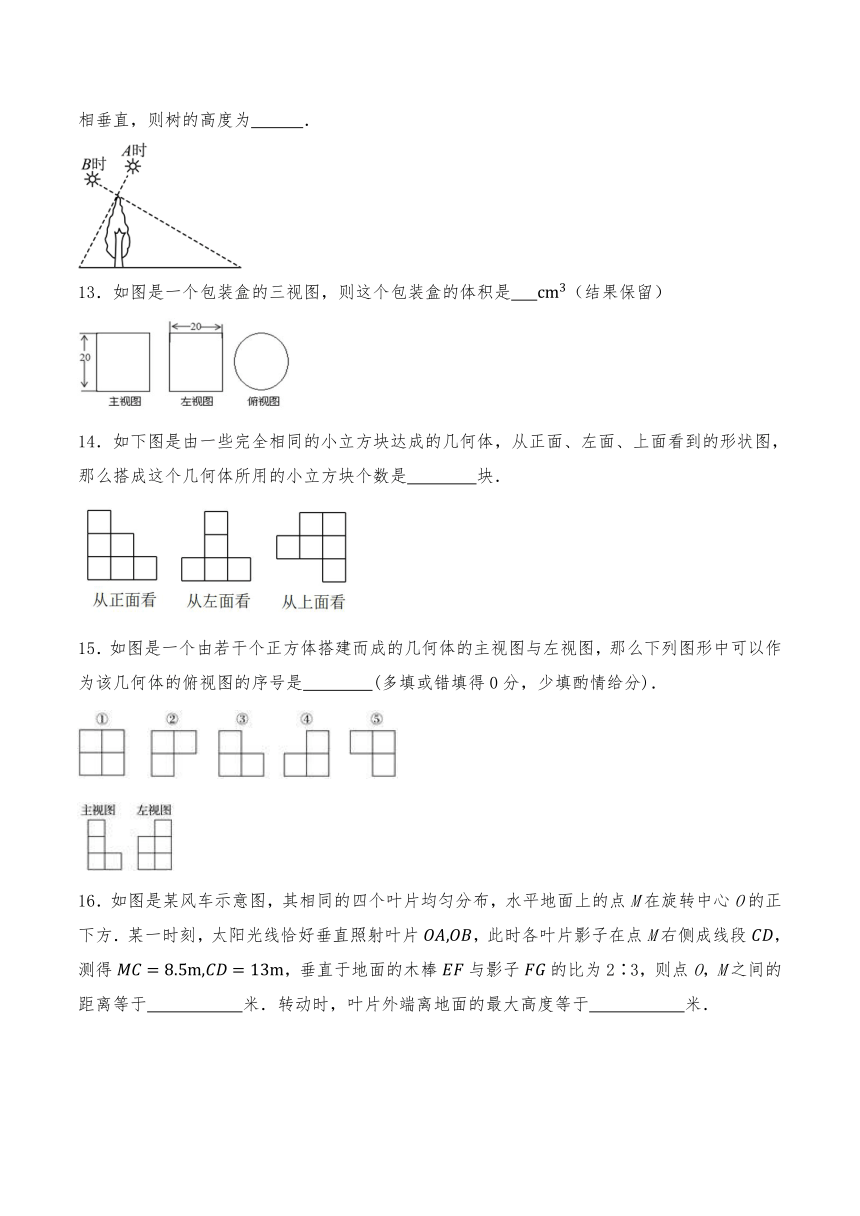
5.如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( )
A. B. C. D.
6.如图是由四个相同的小正方体组成的立体图形,若再增加一块相同的正方体,使主视图和左视图都不变,第五块正方体摆放的位置有个.( )
A. B. C. D.
7.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
8.用一些完全相同的小正方体摆成一个几何体,如图是该几何体的左视图和俯视图,针对该几何体所需小正方体的个数m,三人的说法如下,
甲:若,则该几何体有两种摆法;
乙:若,则该几何体有三种摆法;
丙:若,则该几何体只有一种摆法.下列判断正确的是( )
A.甲对,乙错 B.乙和丙都错 C.甲错,乙对 D.乙对,丙错
9.用小立方块搭成的几何体,从正面看和从上面看的形状图如下,则组成这样的几何体需要的立方块个数为( )
A.最多需要8块,最少需要6块 B.最多需要9块,最少需要6块
C.最多需要8块,最少需要7块 D.最多需要9块,最少需要7块
10.在边长为1的正方形铁皮上剪下一个扇形(率径为R)和一个圆形(率径为r),使之恰好围成一个圆锥.嘉嘉说图1剪下的圆和扇形一定不可以围成一个圆锥,淇淇说图中剪下的圆和扇形有可能围成一个圆锥,还需要满足条件R=4r,则( )
A.只有嘉嘉的说法正确 B.只有淇淇的说法正确
C.两个人的说法均正确 D.两人的说法均不正确
二.填空题(共6小题,满分18分,每小题3分)
11.如图为一机器零件的三视图,它的俯视图为正三角形,根据图中所标的尺寸,计算这个几何体的表面积是 .(结果保留根号)
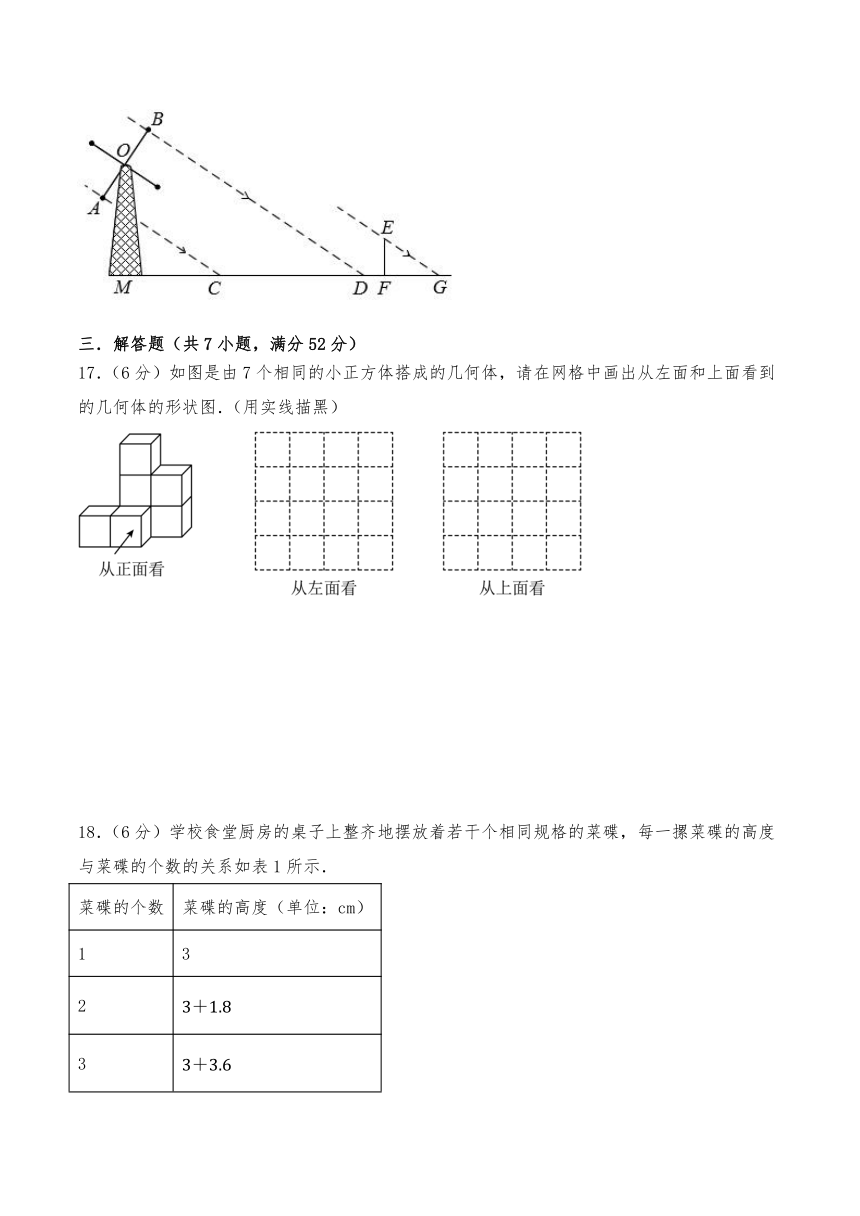
12.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为 .
13.如图是一个包装盒的三视图,则这个包装盒的体积是 (结果保留)
14.如下图是由一些完全相同的小立方块达成的几何体,从正面、左面、上面看到的形状图,那么搭成这个几何体所用的小立方块个数是 块.
15.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分).
16.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.
三.解答题(共7小题,满分52分)
17.(6分)如图是由7个相同的小正方体搭成的几何体,请在网格中画出从左面和上面看到的几何体的形状图.(用实线描黑)
18.(6分)学校食堂厨房的桌子上整齐地摆放着若干个相同规格的菜碟,每一摞菜碟的高度与菜碟的个数的关系如表1所示.
菜碟的个数 菜碟的高度(单位:cm)
1 3
2
3
4
… …
(1)把x个菜碟放成一摞时,请直接写出这一摞菜碟的高度(用含x的式子表示);
(2)如图所示,是几摞菜碟的三视图,厨师想把它们整齐叠成一摞,求叠成一摞后的高度是多少.
19.(8分)物体在太阳光照射下,影子的长度与时间变化直接相关.小明在某天的8点至16点之间,测量了一根米长的直杆垂直于地面时的影子长度,发现影子长度y与时间之间近似二次函数关系,可满足关系式.已知该天11点时影子长度为1.31米,12点时影子长度为1.08米.
(1)请确定a,c的值.
(2)如图,太阳光线和与地面之间的夹角为,求14点时的值.
(3)若另有一垂直于地面的旗杆长度为米,请确定该天9点至14点间这根旗杆影子长度m的范围.
20.(8分)综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.
操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
21.(8分)小明是魔方爱好者,他擅长玩各种魔方,从二阶魔方到九阶魔方,他都能成功复原.有一天,小明突然想到一个问题,在九阶魔方中,到底含有多少个长方体呢?为此,我们先来解决这样一个数学问题:如图,图1是一个长、宽、高分别为a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1的小立方体.这个几何体中一共包含多少个长方体(包括正方体)?(参考公式:1+2+3…+n).
问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:如图2,该几何体有1个小立方体组成,显然,该几何体共有1个长方体.如图3,该几何体有2个小立方体组成,那么它一共包含1+2=3个长方体.如图4,该几何体有3个小立方体组成,那么它一共包含 个长方体.如图5,该几何体﹣共包含210个长方体,那么该几何体共有 个小立方体组成.
探究二:如图6,该几何体有4个小立方体组成,那么它一共包含(1+2)×(1+2)=9个长方体.如图7,该几何体有6个小立方体组成,那么它一共包含 个长方体.如图8,该几何体共有2m个小立方体组成,那么该几何体一共有 个长方体.
探究三:如图1,该几何体共有个a×b×c小立方体组成,那么该几何体共有 个长方体.
探究四:我们现在可以解决小明开始的问题了.在九阶魔方(即a=b=c=9)中,含有 个长方体.
探究五:聪明的小明在学习了三种视图后,又提出一个新的问题:在图1中,若a=6,b=4,c=5,如果拿走一些小立方体后,剩下几何体的三种枧图与原图1的三种视图完全一样,那么最多可以拿走 个小立方体;此时,剩下的几何体的表面积是 .
22.(8分)通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
(1)【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(2)【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为________;
A. B.
C. D.
(3)【解决问题】如图③,河对岸有一灯杆,在灯光下,小明在点D处测得自己的影长,沿方向前进到达点F处测得自己的影长.已知小明的身高为,求灯杆的高度.
23.(8分)(1)一个几何体由一些大小相同的小正方体搭成,如图是从上面看这个几何体的形状图,小正方形中的数字表示在该位置的小正方体的个数,请在网格中画出从正面和左面看到的几何体的形状图.
(2)用小立方块搭一几何体,使它从正面看,从左面看,从上面看得到的图形如图所示.请在从上面看到的图形的小正方形中填人相应的数字,使得小正方形中的数字表示在该位置的小立方块的个数.其中,图1填人的数字表示最多组成该几何体的小立方块的个数,图2填入的数字表示最少组成该几何体的小立方块的个数.
答案解析
一.选择题
1.D
【分析】平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例.
【详解】解:A.影子的方向不相同,故本选项错误;
B. 影子的方向不相同,故本选项错误;
C.相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误;
D. 影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;
故选:D.
2.B
【分析】根据俯视图可知这个几何体,底面有5个正方体,根据主视图及左视图,可知上面有1个正方体,即可得出答案.
【详解】解:根据俯视图可知这个几何体,底面有5个正方体,根据主视图及左视图,可知上面有1个正方体,
搭成这个几何体的小正方体的个数是6,
故选:B.
3.C
【分析】根据平行投影和视图的关系进行判断即可.
【详解】解:A、平行投影中的光线是平行的,故此选项不符合题意;
B、线段的正投影可能是线段,有可能是点,故此选项不符合题意;
C、圆形物体在阳光下的投影可能是椭圆,故此选项符合题意;
D、若两人在路灯下的影子一样长,则两人身高不一定相同,故此选项不符合题意,
故选:C.
4.C
【分析】利用圆锥的底面周长等于侧面展开图的扇形弧长,根据弧长公式计算.
【详解】解:∵圆的半径,
∴圆的周长,
∴这个圆锥侧面展开的扇形的弧长是,
∵扇形的圆心角等于,
∴,
∴这个扇形的半径是.
故选:C.
5.B
【分析】太阳的位置和高度决定了影子的方向和长短.一天中,阳光下物体的影子变化规律是上午影子由长逐渐变短;下午影子由短逐渐变长.方向由西逐渐转向东.
【详解】解:一天中太阳位置的变化规律是:从东到西.太阳的高度变化规律是:低高低.影子位置的变化规律是:从西到东,影子的长短变化规律是:长短长.根据影子变化的特点,按时间顺序给这五张照片排序是.
故选:B.
6.A
【分析】根据组合体的三视图逐项判断即可解答.
【详解】解:再增加一块相同的正方体,使主视图和左视图都不变,第五块正方体摆放的位置只有在图中的阴影部分.
故选:.
7.D
【分析】利用中心投影,延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,证明△PAB∽△PA′B′,然后利用相似比可求出A'B'的长.
【详解】解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB//A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A′B′=6,
故选:D.
8.C
【分析】根据甲、乙、丙所说m的值,分别画出相应几何体的三视图,再进行判断即可.
【详解】解:如图,
甲:若,则第一层已经摆放5个,第二层只放1个,由左视图的俯视图可得主视图如图①②③所示三种,故甲错;
乙:若,则第二层可放2个,可得主视图如④⑤⑥所示三种,故乙对;
丙:若,则第一层放5个,第二层放3个小正方体,这样只能摆放在后面三个小正方体上,主视图如图⑦所示,只有一种摆法,故丙对,
故选:C
9.C
【分析】易得这个几何体共有3层,由俯视图可知第一层正方体的个数为4,由主视图可知第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,相加即可.
【详解】由主视图可得:这个几何体共有3层,
由俯视图可知第一层正方体的个数为4,
由主视图可知第二层最少为2块,最多的正方体的个数为3块,
第三层只有一块,
故:最多为3+4+1=8个
最少为2+4+1=7个
故选C
10.C
【分析】根据图1可知正方形的边长为R,则可求出正方形的对角线长为,即R+2r=,当扇形的弧长等于底面圆(小圆)的周长时,剪下的圆和扇形才可以围成一个圆锥,根据扇形的弧长和圆的周长公式可以得到,代入R+2r=中,即可判断嘉嘉的说法是否正确;图11-2中正方形的边长不再是R,所以不再满足R+2r=,根据淇淇所说的,当R=4r时,可得扇形的弧长=2πr,即得到扇形的弧长等于小圆的周长,从而可判断淇淇的说法是否正确.
【详解】解:由图1可知正方形的边长为R,
∴正方形的对角线=,
∴R+2r=,
∵l扇形=,C小圆=2πr,
要使剪下的圆和扇形才可以围成一个圆锥,则扇形的弧长等于底面圆(小圆)的周长,
∴,
∴,
将代入R+2r,得
≠,
∴图1剪下的圆和扇形一定不可以围成一个圆锥,
∴嘉嘉说的对,
∵图2中正方形的边长不再是R,
∴不再满足R+2r=,
当R=4r时,l扇形=,
∵C小圆=2πr,
∴l扇形= C小圆,
∴淇淇说的对
故选C.
二.填空题
11.32+96
【分析】根据三视图可得机器零件为正三棱柱,三棱柱的上下底是高为4的等边三角形,三棱柱高为4,求出等边三角形边长,求出表面积即可.
【详解】解: 由三视图得机器零件为正三棱柱,
作CD⊥AB于D,
∵△ABC是正三角形,
在Rt△BCD中,
∴ .
故答案为:32+96
12.8m
【分析】根据题意,画出示意图,易得:,进而可得;即,代入数据可得答案.
【详解】解:如图:过点C作,
由题意得:△EFC是直角三角形,,
∵,
∴,
∴,
∴,
∴;即,
由题意得:,
∴,
(负值舍去),
故答案为:8m.
13..
【分析】由图可知包装盒是圆柱体,直径20cm,高20cm,由此求圆柱体体积即可.
【详解】由图知此包装盒是圆柱体,底面圆的直径是20cm,高是20cm,
∴(),
故填: .
14.9
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】解:综合主视图,俯视图,左视图,可得:
底层有6个小正方体,第二层有2个小正方体,第三层有1个小正方体,
所以搭成这个几何体所用的小立方块的个数是6+2+1=9,
故答案为:9.
15.①②③
【分析】根据几何体的主视图和左视图用正方体实物搭出图形判断,或者根据主视图和左视图想象出每个位置正方体的个数进行计算.
【详解】综合左视图跟主视图,从正面看,第1行第1列有3个正方体,第1行第2列有1个或第2行第2列有1个或都有1个,第2行第1列有2个正方体,第2行第1列有2个正方体.
故答案为: ①②③.
16. 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,
由题意可知,点O是AB的中点,
∵,
∴点H是CD的中点,
∵,
∴,
∴,
又∵由题意可知:,
∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,
∴,
∵由题意可知:,
又∵,
∴,
∴,
∴,
∴,,
∵,
∴四边形OHDJ是平行四边形,
∴,
∵,
∴,,,
∵在中,由勾股定理得:,
∴,
∴,
∴,
∴叶片外端离地面的最大高度等于,
故答案为:10,.
三.解答题
17.
18.(1)由表格可知,每增加一个碟子高度增加,
∴当桌子上放有x个碟子时,碟子的高度是;
(2)由三视图知这四摞碟子一共有个碟子,
由(1)知每个碟子的高度为,
∴叠成一摞后碟子的高度为.
19.(1)解:由题意可知,代入函数解析式得,
把,代入函数解析式得,
即,
解得.
(2)解:由(1)得函数解析式为,
把代入得,
则.
(3)解:∵,
∴当时,y取得最小值,,
当时,y取得最大值,,
∵旗杆与直杆的长度比为,
∴,
∴m的取值范围为,
即.
20.解:(1)由图3可得,从上面看这个长方体得到的平面图形为:
(2) 若选A题:由题可得,从上面看这个长方体得到的平面图形为:
若选B题:由题可得,从上面看这个长方体得到的平面图形为:
21.解:探究一:由题意得图4一共有:1+2+3=6个长方体,
∵有1个小正方体组成的几何体有个长方体,有2个小正方体组成的几何体有个长方体,有3个小正方体组成的几何体有个长方体......
∴可以得出规律有n小正方体组成的几何体有个长方体,
∴,即,
解得或(舍去),
故答案为:6,20;
探究二:图6中长一共有1+2=3条线段,宽有1+2=3条线段,高有1条线段,
∴那么它一共包含(1+2)×(1+2)×1=9个长方体,
图7中长一共有1+2+3条线段,宽有1+2=3条线段,高有1条线段,
∴图7中它一共包含(1+2+3)×(1+2)×1=18个长方体,
故答案为:18;
探究三:∵该几何体共有个a×b×c小立方体组成,
∴该几何体有长有条线段,宽有条线段,宽有条线段,
∴图1中一共包含个长方体,
故答案为:;
探究四:由探究三可知,在九阶魔方(即a=b=c=9)中,含有个长方体;
探究五:∵拿走前后的三视图需要一样,
∴只需要保留三视图三个面的几何体图形一样即可, 如图小方格内的数字表示此处一共有多少个小正方体,此时一共有48个小正方体,即为所求,
∴一共最多可以拿走6×5×4-48=72个小正方体,
①当剩下正方体按如下俯视图摆放时,
表面积为:6×5×2+(3+5)×2+6×4×2=124
②当正方体如图摆放时,
相对于①,此时面积增加16,表面积为124+16=142
③同理,当正方体如图摆放时,
相对于①,此时面积增加32,表面积为124+32=158
④当正方体如图摆放时,
相对于①,此时面积增加40,表面积为124+40=164
故答案为:124或142或158或164
22.(1)解:[画图操作]光源的位置及第三根旗杆在该灯光下的影长如图①所示;
(2)[数学思考]如图②所示,等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以小明的影长从到的变化是先越来越短再越来越长;
故答案为:D;
(3)[解决问题],
,,
,,
又,
,
,,,,
,
,,
,
解得:;
灯杆的高度为.
23.解:(1)从正面看分左中右三列,左边列有2个正方形,中间列有3个正方形,右边列有4个正方形,如图
从左边看分左中右三列,左边列1个正方形,中间列4个正方形,右边列2个正方形,
如图所示:
(2)从正面看分左中右三例,左边列3个正方形,中间列1个正方形,右边列2个正方形,
从左面看,分两行,前行后行,前行2个正方形,后行3个正方形,
左列前行可以是1个正方体或两个正方体,,左列后行3个正方体,中间列只有前行1个正方体,右边列前行2个正方体,后列可以1个或2个正方体,最多10个正方体如图1,最少8个正方体如图2.
根据题意,填图如下:
一.选择题(共10小题,满分30分,每小题3分)
1.在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A. B.
C. D.
2.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( )
A.5 B.6 C.7 D.8
3.下列关于投影的说法正确的是( )
A.平行投影中的光线是聚成一点的
B.线段的正投影还是线段
C.圆形物体在阳光下的投影可能是椭圆
D.若两人在路灯下的影子一样长,则两人身高也相同
4.如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径,扇形的圆心角等于,则围成的圆锥的母线长R的值为( )
A.2 B.4 C.8 D.10
5.如图是嘉淇在室外用手机拍下大树的影子随太阳转动情况的照片(上午8时至下午5时之间),这五张照片拍摄的时间先后顺序是( )
A. B. C. D.
6.如图是由四个相同的小正方体组成的立体图形,若再增加一块相同的正方体,使主视图和左视图都不变,第五块正方体摆放的位置有个.( )
A. B. C. D.
7.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
8.用一些完全相同的小正方体摆成一个几何体,如图是该几何体的左视图和俯视图,针对该几何体所需小正方体的个数m,三人的说法如下,
甲:若,则该几何体有两种摆法;
乙:若,则该几何体有三种摆法;
丙:若,则该几何体只有一种摆法.下列判断正确的是( )
A.甲对,乙错 B.乙和丙都错 C.甲错,乙对 D.乙对,丙错
9.用小立方块搭成的几何体,从正面看和从上面看的形状图如下,则组成这样的几何体需要的立方块个数为( )
A.最多需要8块,最少需要6块 B.最多需要9块,最少需要6块
C.最多需要8块,最少需要7块 D.最多需要9块,最少需要7块
10.在边长为1的正方形铁皮上剪下一个扇形(率径为R)和一个圆形(率径为r),使之恰好围成一个圆锥.嘉嘉说图1剪下的圆和扇形一定不可以围成一个圆锥,淇淇说图中剪下的圆和扇形有可能围成一个圆锥,还需要满足条件R=4r,则( )
A.只有嘉嘉的说法正确 B.只有淇淇的说法正确
C.两个人的说法均正确 D.两人的说法均不正确
二.填空题(共6小题,满分18分,每小题3分)
11.如图为一机器零件的三视图,它的俯视图为正三角形,根据图中所标的尺寸,计算这个几何体的表面积是 .(结果保留根号)
12.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为 .
13.如图是一个包装盒的三视图,则这个包装盒的体积是 (结果保留)
14.如下图是由一些完全相同的小立方块达成的几何体,从正面、左面、上面看到的形状图,那么搭成这个几何体所用的小立方块个数是 块.
15.如图是一个由若干个正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分).
16.如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片,此时各叶片影子在点M右侧成线段,测得,垂直于地面的木棒与影子的比为2∶3,则点O,M之间的距离等于 米.转动时,叶片外端离地面的最大高度等于 米.
三.解答题(共7小题,满分52分)
17.(6分)如图是由7个相同的小正方体搭成的几何体,请在网格中画出从左面和上面看到的几何体的形状图.(用实线描黑)
18.(6分)学校食堂厨房的桌子上整齐地摆放着若干个相同规格的菜碟,每一摞菜碟的高度与菜碟的个数的关系如表1所示.
菜碟的个数 菜碟的高度(单位:cm)
1 3
2
3
4
… …
(1)把x个菜碟放成一摞时,请直接写出这一摞菜碟的高度(用含x的式子表示);
(2)如图所示,是几摞菜碟的三视图,厨师想把它们整齐叠成一摞,求叠成一摞后的高度是多少.
19.(8分)物体在太阳光照射下,影子的长度与时间变化直接相关.小明在某天的8点至16点之间,测量了一根米长的直杆垂直于地面时的影子长度,发现影子长度y与时间之间近似二次函数关系,可满足关系式.已知该天11点时影子长度为1.31米,12点时影子长度为1.08米.
(1)请确定a,c的值.
(2)如图,太阳光线和与地面之间的夹角为,求14点时的值.
(3)若另有一垂直于地面的旗杆长度为米,请确定该天9点至14点间这根旗杆影子长度m的范围.
20.(8分)综合与实践
问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.
操作探究:
(1)如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;
(2)已知一个长方体是按上述方式拼成的,组成它的正方体不超过10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.
请从A,B两题中任选一题作答,我选择 题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
21.(8分)小明是魔方爱好者,他擅长玩各种魔方,从二阶魔方到九阶魔方,他都能成功复原.有一天,小明突然想到一个问题,在九阶魔方中,到底含有多少个长方体呢?为此,我们先来解决这样一个数学问题:如图,图1是一个长、宽、高分别为a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整数)的长方体,被分成了a×b×c个棱长为1的小立方体.这个几何体中一共包含多少个长方体(包括正方体)?(参考公式:1+2+3…+n).
问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.
探究一:如图2,该几何体有1个小立方体组成,显然,该几何体共有1个长方体.如图3,该几何体有2个小立方体组成,那么它一共包含1+2=3个长方体.如图4,该几何体有3个小立方体组成,那么它一共包含 个长方体.如图5,该几何体﹣共包含210个长方体,那么该几何体共有 个小立方体组成.
探究二:如图6,该几何体有4个小立方体组成,那么它一共包含(1+2)×(1+2)=9个长方体.如图7,该几何体有6个小立方体组成,那么它一共包含 个长方体.如图8,该几何体共有2m个小立方体组成,那么该几何体一共有 个长方体.
探究三:如图1,该几何体共有个a×b×c小立方体组成,那么该几何体共有 个长方体.
探究四:我们现在可以解决小明开始的问题了.在九阶魔方(即a=b=c=9)中,含有 个长方体.
探究五:聪明的小明在学习了三种视图后,又提出一个新的问题:在图1中,若a=6,b=4,c=5,如果拿走一些小立方体后,剩下几何体的三种枧图与原图1的三种视图完全一样,那么最多可以拿走 个小立方体;此时,剩下的几何体的表面积是 .
22.(8分)通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
(1)【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
(2)【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为________;
A. B.
C. D.
(3)【解决问题】如图③,河对岸有一灯杆,在灯光下,小明在点D处测得自己的影长,沿方向前进到达点F处测得自己的影长.已知小明的身高为,求灯杆的高度.
23.(8分)(1)一个几何体由一些大小相同的小正方体搭成,如图是从上面看这个几何体的形状图,小正方形中的数字表示在该位置的小正方体的个数,请在网格中画出从正面和左面看到的几何体的形状图.
(2)用小立方块搭一几何体,使它从正面看,从左面看,从上面看得到的图形如图所示.请在从上面看到的图形的小正方形中填人相应的数字,使得小正方形中的数字表示在该位置的小立方块的个数.其中,图1填人的数字表示最多组成该几何体的小立方块的个数,图2填入的数字表示最少组成该几何体的小立方块的个数.
答案解析
一.选择题
1.D
【分析】平行投影特点:在同一时刻,不同物体的影子同向,且不同物体的物高和影长成比例.
【详解】解:A.影子的方向不相同,故本选项错误;
B. 影子的方向不相同,故本选项错误;
C.相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,故本选项错误;
D. 影子平行,且较高的树的影子长度大于较低的树的影子,故本选项正确;
故选:D.
2.B
【分析】根据俯视图可知这个几何体,底面有5个正方体,根据主视图及左视图,可知上面有1个正方体,即可得出答案.
【详解】解:根据俯视图可知这个几何体,底面有5个正方体,根据主视图及左视图,可知上面有1个正方体,
搭成这个几何体的小正方体的个数是6,
故选:B.
3.C
【分析】根据平行投影和视图的关系进行判断即可.
【详解】解:A、平行投影中的光线是平行的,故此选项不符合题意;
B、线段的正投影可能是线段,有可能是点,故此选项不符合题意;
C、圆形物体在阳光下的投影可能是椭圆,故此选项符合题意;
D、若两人在路灯下的影子一样长,则两人身高不一定相同,故此选项不符合题意,
故选:C.
4.C
【分析】利用圆锥的底面周长等于侧面展开图的扇形弧长,根据弧长公式计算.
【详解】解:∵圆的半径,
∴圆的周长,
∴这个圆锥侧面展开的扇形的弧长是,
∵扇形的圆心角等于,
∴,
∴这个扇形的半径是.
故选:C.
5.B
【分析】太阳的位置和高度决定了影子的方向和长短.一天中,阳光下物体的影子变化规律是上午影子由长逐渐变短;下午影子由短逐渐变长.方向由西逐渐转向东.
【详解】解:一天中太阳位置的变化规律是:从东到西.太阳的高度变化规律是:低高低.影子位置的变化规律是:从西到东,影子的长短变化规律是:长短长.根据影子变化的特点,按时间顺序给这五张照片排序是.
故选:B.
6.A
【分析】根据组合体的三视图逐项判断即可解答.
【详解】解:再增加一块相同的正方体,使主视图和左视图都不变,第五块正方体摆放的位置只有在图中的阴影部分.
故选:.
7.D
【分析】利用中心投影,延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,证明△PAB∽△PA′B′,然后利用相似比可求出A'B'的长.
【详解】解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB//A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A′B′=6,
故选:D.
8.C
【分析】根据甲、乙、丙所说m的值,分别画出相应几何体的三视图,再进行判断即可.
【详解】解:如图,
甲:若,则第一层已经摆放5个,第二层只放1个,由左视图的俯视图可得主视图如图①②③所示三种,故甲错;
乙:若,则第二层可放2个,可得主视图如④⑤⑥所示三种,故乙对;
丙:若,则第一层放5个,第二层放3个小正方体,这样只能摆放在后面三个小正方体上,主视图如图⑦所示,只有一种摆法,故丙对,
故选:C
9.C
【分析】易得这个几何体共有3层,由俯视图可知第一层正方体的个数为4,由主视图可知第二层最少为2块,最多的正方体的个数为3块,第三层只有一块,相加即可.
【详解】由主视图可得:这个几何体共有3层,
由俯视图可知第一层正方体的个数为4,
由主视图可知第二层最少为2块,最多的正方体的个数为3块,
第三层只有一块,
故:最多为3+4+1=8个
最少为2+4+1=7个
故选C
10.C
【分析】根据图1可知正方形的边长为R,则可求出正方形的对角线长为,即R+2r=,当扇形的弧长等于底面圆(小圆)的周长时,剪下的圆和扇形才可以围成一个圆锥,根据扇形的弧长和圆的周长公式可以得到,代入R+2r=中,即可判断嘉嘉的说法是否正确;图11-2中正方形的边长不再是R,所以不再满足R+2r=,根据淇淇所说的,当R=4r时,可得扇形的弧长=2πr,即得到扇形的弧长等于小圆的周长,从而可判断淇淇的说法是否正确.
【详解】解:由图1可知正方形的边长为R,
∴正方形的对角线=,
∴R+2r=,
∵l扇形=,C小圆=2πr,
要使剪下的圆和扇形才可以围成一个圆锥,则扇形的弧长等于底面圆(小圆)的周长,
∴,
∴,
将代入R+2r,得
≠,
∴图1剪下的圆和扇形一定不可以围成一个圆锥,
∴嘉嘉说的对,
∵图2中正方形的边长不再是R,
∴不再满足R+2r=,
当R=4r时,l扇形=,
∵C小圆=2πr,
∴l扇形= C小圆,
∴淇淇说的对
故选C.
二.填空题
11.32+96
【分析】根据三视图可得机器零件为正三棱柱,三棱柱的上下底是高为4的等边三角形,三棱柱高为4,求出等边三角形边长,求出表面积即可.
【详解】解: 由三视图得机器零件为正三棱柱,
作CD⊥AB于D,
∵△ABC是正三角形,
在Rt△BCD中,
∴ .
故答案为:32+96
12.8m
【分析】根据题意,画出示意图,易得:,进而可得;即,代入数据可得答案.
【详解】解:如图:过点C作,
由题意得:△EFC是直角三角形,,
∵,
∴,
∴,
∴,
∴;即,
由题意得:,
∴,
(负值舍去),
故答案为:8m.
13..
【分析】由图可知包装盒是圆柱体,直径20cm,高20cm,由此求圆柱体体积即可.
【详解】由图知此包装盒是圆柱体,底面圆的直径是20cm,高是20cm,
∴(),
故填: .
14.9
【分析】从俯视图中可以看出最底层小正方体的个数及形状,从主视图和左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】解:综合主视图,俯视图,左视图,可得:
底层有6个小正方体,第二层有2个小正方体,第三层有1个小正方体,
所以搭成这个几何体所用的小立方块的个数是6+2+1=9,
故答案为:9.
15.①②③
【分析】根据几何体的主视图和左视图用正方体实物搭出图形判断,或者根据主视图和左视图想象出每个位置正方体的个数进行计算.
【详解】综合左视图跟主视图,从正面看,第1行第1列有3个正方体,第1行第2列有1个或第2行第2列有1个或都有1个,第2行第1列有2个正方体,第2行第1列有2个正方体.
故答案为: ①②③.
16. 10
【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据,求出OM的长度,证明,得出,,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.
【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,
由题意可知,点O是AB的中点,
∵,
∴点H是CD的中点,
∵,
∴,
∴,
又∵由题意可知:,
∴,解得,
∴点O、M之间的距离等于,
∵BI⊥OJ,
∴,
∵由题意可知:,
又∵,
∴,
∴,
∴,
∴,,
∵,
∴四边形OHDJ是平行四边形,
∴,
∵,
∴,,,
∵在中,由勾股定理得:,
∴,
∴,
∴,
∴叶片外端离地面的最大高度等于,
故答案为:10,.
三.解答题
17.
18.(1)由表格可知,每增加一个碟子高度增加,
∴当桌子上放有x个碟子时,碟子的高度是;
(2)由三视图知这四摞碟子一共有个碟子,
由(1)知每个碟子的高度为,
∴叠成一摞后碟子的高度为.
19.(1)解:由题意可知,代入函数解析式得,
把,代入函数解析式得,
即,
解得.
(2)解:由(1)得函数解析式为,
把代入得,
则.
(3)解:∵,
∴当时,y取得最小值,,
当时,y取得最大值,,
∵旗杆与直杆的长度比为,
∴,
∴m的取值范围为,
即.
20.解:(1)由图3可得,从上面看这个长方体得到的平面图形为:
(2) 若选A题:由题可得,从上面看这个长方体得到的平面图形为:
若选B题:由题可得,从上面看这个长方体得到的平面图形为:
21.解:探究一:由题意得图4一共有:1+2+3=6个长方体,
∵有1个小正方体组成的几何体有个长方体,有2个小正方体组成的几何体有个长方体,有3个小正方体组成的几何体有个长方体......
∴可以得出规律有n小正方体组成的几何体有个长方体,
∴,即,
解得或(舍去),
故答案为:6,20;
探究二:图6中长一共有1+2=3条线段,宽有1+2=3条线段,高有1条线段,
∴那么它一共包含(1+2)×(1+2)×1=9个长方体,
图7中长一共有1+2+3条线段,宽有1+2=3条线段,高有1条线段,
∴图7中它一共包含(1+2+3)×(1+2)×1=18个长方体,
故答案为:18;
探究三:∵该几何体共有个a×b×c小立方体组成,
∴该几何体有长有条线段,宽有条线段,宽有条线段,
∴图1中一共包含个长方体,
故答案为:;
探究四:由探究三可知,在九阶魔方(即a=b=c=9)中,含有个长方体;
探究五:∵拿走前后的三视图需要一样,
∴只需要保留三视图三个面的几何体图形一样即可, 如图小方格内的数字表示此处一共有多少个小正方体,此时一共有48个小正方体,即为所求,
∴一共最多可以拿走6×5×4-48=72个小正方体,
①当剩下正方体按如下俯视图摆放时,
表面积为:6×5×2+(3+5)×2+6×4×2=124
②当正方体如图摆放时,
相对于①,此时面积增加16,表面积为124+16=142
③同理,当正方体如图摆放时,
相对于①,此时面积增加32,表面积为124+32=158
④当正方体如图摆放时,
相对于①,此时面积增加40,表面积为124+40=164
故答案为:124或142或158或164
22.(1)解:[画图操作]光源的位置及第三根旗杆在该灯光下的影长如图①所示;
(2)[数学思考]如图②所示,等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以小明的影长从到的变化是先越来越短再越来越长;
故答案为:D;
(3)[解决问题],
,,
,,
又,
,
,,,,
,
,,
,
解得:;
灯杆的高度为.
23.解:(1)从正面看分左中右三列,左边列有2个正方形,中间列有3个正方形,右边列有4个正方形,如图
从左边看分左中右三列,左边列1个正方形,中间列4个正方形,右边列2个正方形,
如图所示:
(2)从正面看分左中右三例,左边列3个正方形,中间列1个正方形,右边列2个正方形,
从左面看,分两行,前行后行,前行2个正方形,后行3个正方形,
左列前行可以是1个正方体或两个正方体,,左列后行3个正方体,中间列只有前行1个正方体,右边列前行2个正方体,后列可以1个或2个正方体,最多10个正方体如图1,最少8个正方体如图2.
根据题意,填图如下:
