13.5全等三角形的判定课件(北京课改版八年级上)(三)
文档属性
| 名称 | 13.5全等三角形的判定课件(北京课改版八年级上)(三) |

|
|
| 格式 | rar | ||
| 文件大小 | 193.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-21 00:00:00 | ||
图片预览



文档简介
课件10张PPT。13.5全等三角形的判定全等三角形的判定
————角边角公理目的要求
引入新课
讲解新课
巩固新课
布置作业
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现公理,并用之解决问题。
重点难点:
1、重点:熟悉判定两三角形全等的角边角公理。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。引入新课:
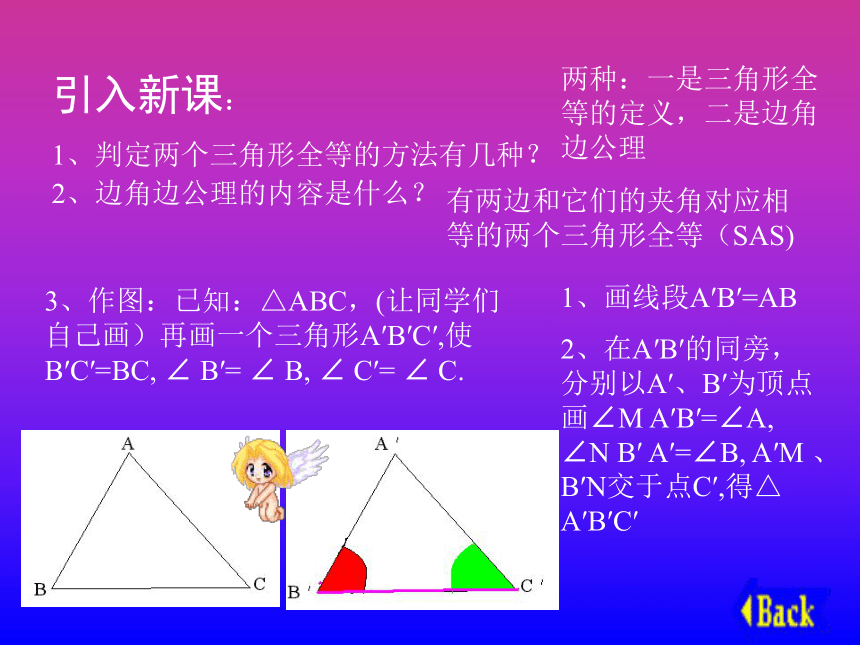
1、判定两个三角形全等的方法有几种?两种:一是三角形全等的定义,二是边角边公理2、边角边公理的内容是什么?有两边和它们的夹角对应相等的两个三角形全等(SAS)3、作图:已知:△ABC,(让同学们自己画)再画一个三角形A′B′C′,使B′C′=BC, ∠ B′= ∠ B, ∠ C′= ∠ C.
1、画线段A′B′=AB
2、在A′B′的同旁,分别以A′、B′为顶点画∠M A′B′=∠A, ∠N B′ A′=∠B, A′M 、B′N交于点C′,得△ A′B′C′讲解新课 ( 1 )
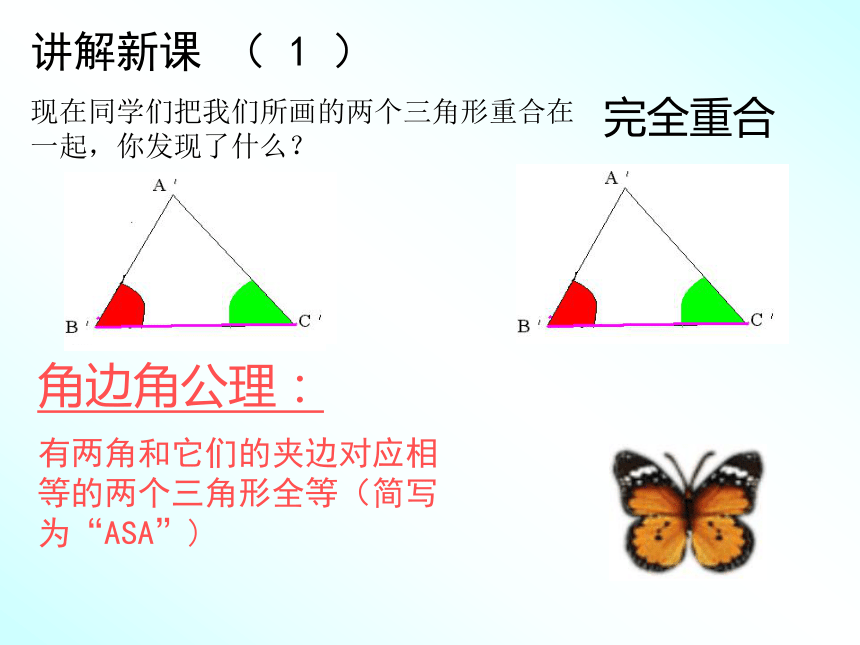
现在同学们把我们所画的两个三角形重合在一起,你发现了什么?完全重合角边角公理:
有两角和它们的夹边对应相等的两个三角形全等(简写为“ASA”)
讲解新课( 2 )
例1、已知:如图,∠DAB=∠CAB,∠C=∠D
求证:AC=AD分析:要证AC=AD,只需证明△ACB≌△ADB,根据三角形内角和定理和“ASA”公理即可。证明:∵ ∠DAB=∠CAB,∠C=∠D∴∠ABD=∠ACD (三角形内角和定理)在△ACB和△ADB中 ∠DAB=∠CAB
AB=AB (共用边)
∠ABD=∠ACD
∴ △ACB≌△ADB (ASA)∴AC=AD讲解新课( 3 )
例2、已知:点D在AB上,点E在AC上,BE和CD交于O点,AB=AC,∠B=∠C. 求证:BD=CE
分析:欲证BD=CE,首先看BD、CE在哪里,BD在△BOD中,CE在△COE中,欲得BD=CE就得证明△BOD≌△COE,由于∠B=∠C,∠BOD=∠COE,尚差它们的夹边BO=CO,而BO、CO还在△BOD和△COE中,不能证明,而AB=AC这个条件尚未应用,所以要证BD=CE,只要证AD=AE即可,由于∠B=∠C、∠A= ∠A、 AB=AC,即可推出△ABE≌△ACD全等,从而得到AD=AE,即可获得BD=CE。证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C∴ △ABE≌△ACD (ASA)∴AD=AE ∵AB=AC ∴BD=CE巩固新课:一、判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两角和其中一角的平分线对应相等的两个三角形全等。( )
二、填空题:
1、如图,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。
三、下列条件能否判定△ABC≌△DEF.
1、∠A=∠E AB=EF ∠B=∠D
2、∠A=∠D AB=DE ∠B=∠E
四、求证:全等三角形的对应角平分线相等。
(1图)布置作业:
1、如右图:已知,∠ABE=∠CBD, ∠BCE=∠DBA,EC=AD
求证:AB=BE,BC=DB
2、如右图:已知,AD,BE,BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
欢迎指导,再见!
————角边角公理目的要求
引入新课
讲解新课
巩固新课
布置作业
目的要求:
1、使学生理解判定两三角形全等的角边角公理,并能运用这个方法证明线段或角的相等。
2、通过画图发现公理,并用之解决问题。
重点难点:
1、重点:熟悉判定两三角形全等的角边角公理。
2、难点:通过两个三角形全等,间接证明线段或角相等及两线平行、垂直等。引入新课:
1、判定两个三角形全等的方法有几种?两种:一是三角形全等的定义,二是边角边公理2、边角边公理的内容是什么?有两边和它们的夹角对应相等的两个三角形全等(SAS)3、作图:已知:△ABC,(让同学们自己画)再画一个三角形A′B′C′,使B′C′=BC, ∠ B′= ∠ B, ∠ C′= ∠ C.
1、画线段A′B′=AB
2、在A′B′的同旁,分别以A′、B′为顶点画∠M A′B′=∠A, ∠N B′ A′=∠B, A′M 、B′N交于点C′,得△ A′B′C′讲解新课 ( 1 )
现在同学们把我们所画的两个三角形重合在一起,你发现了什么?完全重合角边角公理:
有两角和它们的夹边对应相等的两个三角形全等(简写为“ASA”)
讲解新课( 2 )
例1、已知:如图,∠DAB=∠CAB,∠C=∠D
求证:AC=AD分析:要证AC=AD,只需证明△ACB≌△ADB,根据三角形内角和定理和“ASA”公理即可。证明:∵ ∠DAB=∠CAB,∠C=∠D∴∠ABD=∠ACD (三角形内角和定理)在△ACB和△ADB中 ∠DAB=∠CAB
AB=AB (共用边)
∠ABD=∠ACD
∴ △ACB≌△ADB (ASA)∴AC=AD讲解新课( 3 )
例2、已知:点D在AB上,点E在AC上,BE和CD交于O点,AB=AC,∠B=∠C. 求证:BD=CE
分析:欲证BD=CE,首先看BD、CE在哪里,BD在△BOD中,CE在△COE中,欲得BD=CE就得证明△BOD≌△COE,由于∠B=∠C,∠BOD=∠COE,尚差它们的夹边BO=CO,而BO、CO还在△BOD和△COE中,不能证明,而AB=AC这个条件尚未应用,所以要证BD=CE,只要证AD=AE即可,由于∠B=∠C、∠A= ∠A、 AB=AC,即可推出△ABE≌△ACD全等,从而得到AD=AE,即可获得BD=CE。证明:在△ABE和△ACD中 ∠A= ∠A
AB=AC
∠B=∠C∴ △ABE≌△ACD (ASA)∴AD=AE ∵AB=AC ∴BD=CE巩固新课:一、判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两角和其中一角的平分线对应相等的两个三角形全等。( )
二、填空题:
1、如图,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。
三、下列条件能否判定△ABC≌△DEF.
1、∠A=∠E AB=EF ∠B=∠D
2、∠A=∠D AB=DE ∠B=∠E
四、求证:全等三角形的对应角平分线相等。
(1图)布置作业:
1、如右图:已知,∠ABE=∠CBD, ∠BCE=∠DBA,EC=AD
求证:AB=BE,BC=DB
2、如右图:已知,AD,BE,BC交于O,且AO=OD,BO=OC,EO=OF
求证:△AEB≌△DFC
欢迎指导,再见!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
