【沪科版八上同步练习】11.1 平面内点的坐标(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】11.1 平面内点的坐标(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
11.1平面内点的坐标
一、单选题
1.根据下列描述,能够确定一个点的位置的是( )
A.省博物馆东侧 B.体育馆东面看台第排
C.第节车厢,号座位 D.学校图书馆前面
2.已知 在第一象限内,且点P到两坐标轴的距离相等,则 的值为( )
A.2 B.3 C.-6 D.2或-6
3.红领巾公园健走步道环湖而建,以红军长征路为主题,如图是利用平面直角坐标系画出的健走步道路线上主要地点的大致分布图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示遵义的点的坐标为(-5,7),表示腊子口的点的坐标为(4,-1),那么这个平面直角坐标系原点所在位置是( )
A.泸定桥 B.瑞金 C.包座 D.湘江
4.已知点到x轴的距离是5,则a为( )
A.5 B.-5 C.±5 D.±10
5.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段 轴且 ,则点 的坐标是( )
A. 或 B. 或
C. 或 D. 或
二、填空题
6.教材在第七章复习题的“拓广探索”中,曾让同学们探索发现:在平面直角坐标系中,线段中点的横坐标(纵坐标)分别等于对应线段的两个端点的横坐标(纵坐标)和的一半,例如:点,点,则线段的中点的坐标为,请利用以上结论解决问题:在平面直角坐标系中,点,若线段的中点恰好在轴上,且到轴的距离是,则 .
7.点P(-6,8)到x轴的距离是 ,到y轴的距离是 .
8.若点 在 轴上,则m的值为 .
9.若点P(1﹣m,m)在第二象限,则(m﹣1)x>1﹣m的解集为 .
10.如图:观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:
11.如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…, 则第 200 个点的横坐标为 .
三、计算题
12.已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
13.已知点P(a﹣1,3a+9),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等且在第二象限.
四、解答题
14.如图,这是某市部分简图,请以火车站为坐标原点向东的方向为x 轴的正方向,建立平面直角坐标系,并分别写出火车站以北(包括火车站)各地点的坐标.(每个正方形边长是 1)
15.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
16.小明家和学校所在地的简单地图如图所示,已知,点为OP的中点,回答下列问题.
(1)图中距小明家距离相同的是哪些地方
(2)写出学校、商场、公园、停车场相对于小明家的方位角,哪两个地方的方位角是相同的
(3)若学校距离小明家400m,那么商场和停车场分别距离小明家多少米
五、综合题
17.△ABC在方格中,位置如图所示,A点的坐标为(-3,1).
(1)写出B、C两点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请画出平移后的 ;
(3)在x轴上存在点D,使 的面积等于3,求满足条件的点D的坐标.
18.已知当m,n都是实数,且满足2m=8+n时,称p(m﹣1,)为“开心点”.例如点A(5,3)为“开心点”.
因为当A(5,3)时,m﹣1=5,=3,得m=6,n=4,
所以2m=2×6=12,8+n=8+4=12,
所以2m=8+n.
所以A(5,3)是“开心点”.
(1)判断点B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
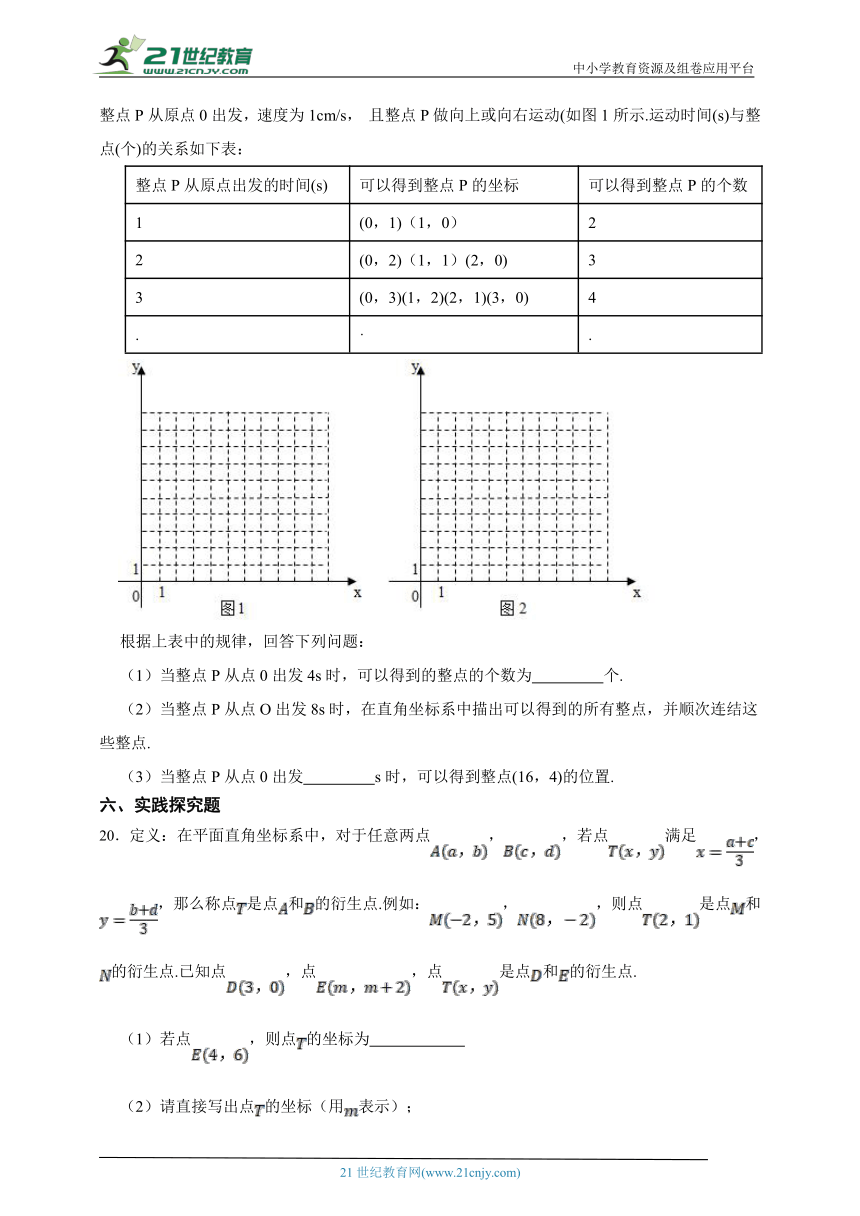
19.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm, 整点P从原点0出发,速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s) 可以得到整点P的坐标 可以得到整点P的个数
1 (0,1)(1,0) 2
2 (0,2)(1,1)(2,0) 3
3 (0,3)(1,2)(2,1)(3,0) 4
. · .
根据上表中的规律,回答下列问题:
(1)当整点P从点0出发4s时,可以得到的整点的个数为 个.
(2)当整点P从点O出发8s时,在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
(3)当整点P从点0出发 s时,可以得到整点(16,4)的位置.
六、实践探究题
20.定义:在平面直角坐标系中,对于任意两点,,若点满足,,那么称点是点和的衍生点.例如:,,则点是点和的衍生点.已知点,点,点是点和的衍生点.
(1)若点,则点的坐标为
(2)请直接写出点的坐标(用表示);
(3)若直线交轴于点,当时,求点的坐标.
答案解析部分
1.【答案】C
【知识点】点的坐标
2.【答案】A
【知识点】点的坐标
3.【答案】B
【知识点】用坐标表示地理位置
4.【答案】C
【知识点】点的坐标
5.【答案】A
【知识点】点的坐标
6.【答案】或
【知识点】点的坐标;坐标与图形性质
7.【答案】8;6
【知识点】点的坐标
8.【答案】2
【知识点】点的坐标
9.【答案】x>﹣1
【知识点】解一元一次不等式;点的坐标
10.【答案】(4,7)
【知识点】用坐标表示地理位置
11.【答案】20
【知识点】点的坐标
12.【答案】(1)
(2)
【知识点】坐标与图形性质;加减消元法解二元一次方程组
13.【答案】(1)解:∵点P(a﹣1,3a+9)在x轴上,
∴3a+9=0,
解得:a=﹣3,
故a﹣1=﹣3﹣1=﹣4,
则P(﹣4,0);
(2)解:∵点P到x轴、y轴的距离相等,
∴a﹣1=3a+9或a﹣1+3a+9=0,
解得:a=﹣5,或a=﹣2,
故当a=﹣5时,a﹣1=﹣6,3a+9=﹣6,
则P(﹣6,﹣6)在第三象限,不合题意,舍去;
故当a=﹣2时,a﹣1=﹣3,3a+9=3,
则P(﹣3,3)在第二象限,符合题意.
综上所述:P(﹣3,3).
【知识点】坐标与图形性质
14.【答案】解:以火车站为坐标原点向东的方向为 x 轴的正方向,建立平面直角坐标系如下所示
由坐标系可知:火车站(0,0),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3).
【知识点】用坐标表示地理位置
15.【答案】解:如图所示:A(0,4),B(﹣3,2),C(﹣2,﹣1),E(3,3),F(0,0).
【知识点】用坐标表示地理位置
16.【答案】(1)解:∵C为OP的中点,
.
.
∴图中距小明家距离相同的是学校和公园;
(2)解:学校在小明家的北偏东45°方向,商场在小明家的北偏西30°方向,公园在小明家的南偏东60°方向,停车场在小明家的南偏东60°方向;公园和停车扬的方位角相同.
(3)解:图上1cm表示,
商场距离小明家.
【知识点】用坐标表示地理位置
17.【答案】(1)解:B(-2,4),C(1,1)
(2)解:△A1B1C1如图所示;
(3)解:△DB1C1的面积= ×C1D×3=3,解得C1D=2,
点D在C1的左边时,OD=3-2=1,
此时,点D(1,0),
点D在C1的右边时,OD=3+2=5,
此时,点D(5,0),
综上所述,点D(1,0)或(5,0).
【知识点】用坐标表示地理位置;坐标与图形性质
18.【答案】(1)解:(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,
解得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)解:点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
【知识点】点的坐标;定义新运算
19.【答案】(1)5
(2)解:由表中所示规律可知,横纵坐标的和等于时间,则点的个数为(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1),(8,0).如图:
(3)20
【知识点】点的坐标
20.【答案】(1)
(2)解:
(3)解:
【知识点】点的坐标;定义新运算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
11.1平面内点的坐标
一、单选题
1.根据下列描述,能够确定一个点的位置的是( )
A.省博物馆东侧 B.体育馆东面看台第排
C.第节车厢,号座位 D.学校图书馆前面
2.已知 在第一象限内,且点P到两坐标轴的距离相等,则 的值为( )
A.2 B.3 C.-6 D.2或-6
3.红领巾公园健走步道环湖而建,以红军长征路为主题,如图是利用平面直角坐标系画出的健走步道路线上主要地点的大致分布图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示遵义的点的坐标为(-5,7),表示腊子口的点的坐标为(4,-1),那么这个平面直角坐标系原点所在位置是( )
A.泸定桥 B.瑞金 C.包座 D.湘江
4.已知点到x轴的距离是5,则a为( )
A.5 B.-5 C.±5 D.±10
5.在平面直角坐标系中,第二象限内的点P到x轴的距离是2,到y轴的距离是3,已知线段 轴且 ,则点 的坐标是( )
A. 或 B. 或
C. 或 D. 或
二、填空题
6.教材在第七章复习题的“拓广探索”中,曾让同学们探索发现:在平面直角坐标系中,线段中点的横坐标(纵坐标)分别等于对应线段的两个端点的横坐标(纵坐标)和的一半,例如:点,点,则线段的中点的坐标为,请利用以上结论解决问题:在平面直角坐标系中,点,若线段的中点恰好在轴上,且到轴的距离是,则 .
7.点P(-6,8)到x轴的距离是 ,到y轴的距离是 .
8.若点 在 轴上,则m的值为 .
9.若点P(1﹣m,m)在第二象限,则(m﹣1)x>1﹣m的解集为 .
10.如图:观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:
11.如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…, 则第 200 个点的横坐标为 .
三、计算题
12.已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
13.已知点P(a﹣1,3a+9),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等且在第二象限.
四、解答题
14.如图,这是某市部分简图,请以火车站为坐标原点向东的方向为x 轴的正方向,建立平面直角坐标系,并分别写出火车站以北(包括火车站)各地点的坐标.(每个正方形边长是 1)
15.王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,﹣2),请你帮她画出坐标系,并写出其他各景点的坐标.
16.小明家和学校所在地的简单地图如图所示,已知,点为OP的中点,回答下列问题.
(1)图中距小明家距离相同的是哪些地方
(2)写出学校、商场、公园、停车场相对于小明家的方位角,哪两个地方的方位角是相同的
(3)若学校距离小明家400m,那么商场和停车场分别距离小明家多少米
五、综合题
17.△ABC在方格中,位置如图所示,A点的坐标为(-3,1).
(1)写出B、C两点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请画出平移后的 ;
(3)在x轴上存在点D,使 的面积等于3,求满足条件的点D的坐标.
18.已知当m,n都是实数,且满足2m=8+n时,称p(m﹣1,)为“开心点”.例如点A(5,3)为“开心点”.
因为当A(5,3)时,m﹣1=5,=3,得m=6,n=4,
所以2m=2×6=12,8+n=8+4=12,
所以2m=8+n.
所以A(5,3)是“开心点”.
(1)判断点B(4,10)是否为“开心点”,并说明理由;
(2)若点M(a,2a﹣1)是“开心点”,请判断点M在第几象限?并说明理由.
19.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm, 整点P从原点0出发,速度为1cm/s, 且整点P做向上或向右运动(如图1所示.运动时间(s)与整点(个)的关系如下表:
整点P从原点出发的时间(s) 可以得到整点P的坐标 可以得到整点P的个数
1 (0,1)(1,0) 2
2 (0,2)(1,1)(2,0) 3
3 (0,3)(1,2)(2,1)(3,0) 4
. · .
根据上表中的规律,回答下列问题:
(1)当整点P从点0出发4s时,可以得到的整点的个数为 个.
(2)当整点P从点O出发8s时,在直角坐标系中描出可以得到的所有整点,并顺次连结这些整点.
(3)当整点P从点0出发 s时,可以得到整点(16,4)的位置.
六、实践探究题
20.定义:在平面直角坐标系中,对于任意两点,,若点满足,,那么称点是点和的衍生点.例如:,,则点是点和的衍生点.已知点,点,点是点和的衍生点.
(1)若点,则点的坐标为
(2)请直接写出点的坐标(用表示);
(3)若直线交轴于点,当时,求点的坐标.
答案解析部分
1.【答案】C
【知识点】点的坐标
2.【答案】A
【知识点】点的坐标
3.【答案】B
【知识点】用坐标表示地理位置
4.【答案】C
【知识点】点的坐标
5.【答案】A
【知识点】点的坐标
6.【答案】或
【知识点】点的坐标;坐标与图形性质
7.【答案】8;6
【知识点】点的坐标
8.【答案】2
【知识点】点的坐标
9.【答案】x>﹣1
【知识点】解一元一次不等式;点的坐标
10.【答案】(4,7)
【知识点】用坐标表示地理位置
11.【答案】20
【知识点】点的坐标
12.【答案】(1)
(2)
【知识点】坐标与图形性质;加减消元法解二元一次方程组
13.【答案】(1)解:∵点P(a﹣1,3a+9)在x轴上,
∴3a+9=0,
解得:a=﹣3,
故a﹣1=﹣3﹣1=﹣4,
则P(﹣4,0);
(2)解:∵点P到x轴、y轴的距离相等,
∴a﹣1=3a+9或a﹣1+3a+9=0,
解得:a=﹣5,或a=﹣2,
故当a=﹣5时,a﹣1=﹣6,3a+9=﹣6,
则P(﹣6,﹣6)在第三象限,不合题意,舍去;
故当a=﹣2时,a﹣1=﹣3,3a+9=3,
则P(﹣3,3)在第二象限,符合题意.
综上所述:P(﹣3,3).
【知识点】坐标与图形性质
14.【答案】解:以火车站为坐标原点向东的方向为 x 轴的正方向,建立平面直角坐标系如下所示
由坐标系可知:火车站(0,0),文化宫(-3,1),体育场(-4,3),宾馆(2,2),市场(4,3).
【知识点】用坐标表示地理位置
15.【答案】解:如图所示:A(0,4),B(﹣3,2),C(﹣2,﹣1),E(3,3),F(0,0).
【知识点】用坐标表示地理位置
16.【答案】(1)解:∵C为OP的中点,
.
.
∴图中距小明家距离相同的是学校和公园;
(2)解:学校在小明家的北偏东45°方向,商场在小明家的北偏西30°方向,公园在小明家的南偏东60°方向,停车场在小明家的南偏东60°方向;公园和停车扬的方位角相同.
(3)解:图上1cm表示,
商场距离小明家.
【知识点】用坐标表示地理位置
17.【答案】(1)解:B(-2,4),C(1,1)
(2)解:△A1B1C1如图所示;
(3)解:△DB1C1的面积= ×C1D×3=3,解得C1D=2,
点D在C1的左边时,OD=3-2=1,
此时,点D(1,0),
点D在C1的右边时,OD=3+2=5,
此时,点D(5,0),
综上所述,点D(1,0)或(5,0).
【知识点】用坐标表示地理位置;坐标与图形性质
18.【答案】(1)解:(4,10)不是“开心点”,理由如下,
当B(4,10)时,m﹣1=4,,
解得m=5,n=18,
则2m=10,8+18=26,
所以2m≠8+n,
所以点B(4,10)不是“开心点”;
(2)解:点M在第三象限,
理由如下:
∵点M(a,2a﹣1)是“开心点”,
∴m﹣1=a,,
∴m=a+1,n=4a﹣4,
代入2m=8+n有2a+2=8+4a﹣4,
∴a=﹣1,2a﹣1=﹣3,
∴M(﹣1,﹣3),
故点M在第三象限.
【知识点】点的坐标;定义新运算
19.【答案】(1)5
(2)解:由表中所示规律可知,横纵坐标的和等于时间,则点的个数为(0,8),(1,7),(2,6),(3,5),(4,4),(5,3),(6,2),(7,1),(8,0).如图:
(3)20
【知识点】点的坐标
20.【答案】(1)
(2)解:
(3)解:
【知识点】点的坐标;定义新运算
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
