【沪科版八上同步练习】 第11章 平面直角坐标系(基础知识)检测题(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 第11章 平面直角坐标系(基础知识)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 11:19:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
第11章平面直角坐标系(基础知识)检测题
一、单选题
1.在平面直角坐标系中,将点A(1,-2)向左平移2个单位长度,再向上平移3个单位长度,得到点A′,则点A的坐标是( )
A.(-1,1) B.(-1,-2)
C.(-1,2) D.(1,2)
2.如果点P( +3, +1)在y轴上,则点P的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,﹣4)
3.如图, 沿着由点 到点 的方向,平移到 ,已知 , ,那么平移的距离为( )
A. B. C. D.
4.在方格中,将图1中的图形平移后位置如图2所示,则下列图形的平移方法中,正确的是( )
A.向上移动1格 B.向下移动1格 C.向上移动2格 D.向下移动2格
5.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟时, 它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动 一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
二、填空题
6.在平面直角坐标系中点A (2 ,1) 关于y 轴对称点的坐标是 .
7.点(-4,3)关于x轴对称的点的坐标为 .
8.将点P(2,-3)向右平移2个单位得到点P1,点P2与点P1关于x轴对称,则P2的坐标是
9.已知点M的坐标为,点N的坐标为(1,5),直线轴,则点M的横坐标为 .
10.如图,在平面直角坐标系中,,,,.把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是 .
11.如图,已知 (1,0), (1,1), (-1,1), (-1,-1), (2,-1)…,则 的坐标是 .
三、计算题
12.已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
13.在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),
(0,4),(-2,0)。
(1)这是一个什么图形?
(2)求出它的面积;
四、解答题
14.如图,长方形中,O为平面直角坐标系的原点,A点的坐标为,C点的坐标为,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着的路线移动(即:沿着长方形移动一周).
(1)点B的坐标为__________;
(2)当P点移动了4秒时,点P的坐标为多少?
(3)在移动过程中,当点P到轴距离为5个单位长度时,则点P移动的时间为多少?
15.如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
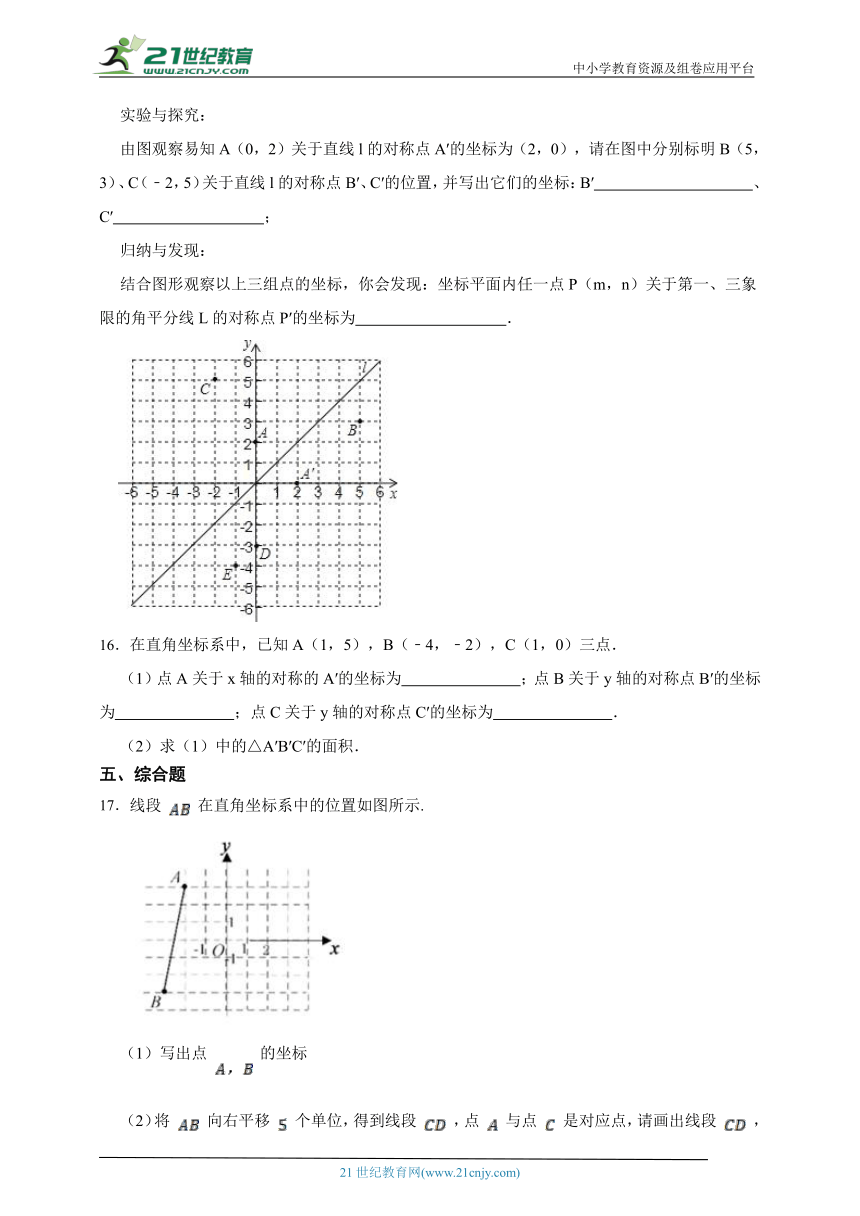
实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′ 、C′ ;
归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线L的对称点P′的坐标为 .
16.在直角坐标系中,已知A(1,5),B(﹣4,﹣2),C(1,0)三点.
(1)点A关于x轴的对称的A′的坐标为 ;点B关于y轴的对称点B′的坐标为 ;点C关于y轴的对称点C′的坐标为 .
(2)求(1)中的△A′B′C′的面积.
五、综合题
17.线段 在直角坐标系中的位置如图所示.
(1)写出点 的坐标
(2)将 向右平移 个单位,得到线段 ,点 与点 是对应点,请画出线段 ,并写出点 的坐标.
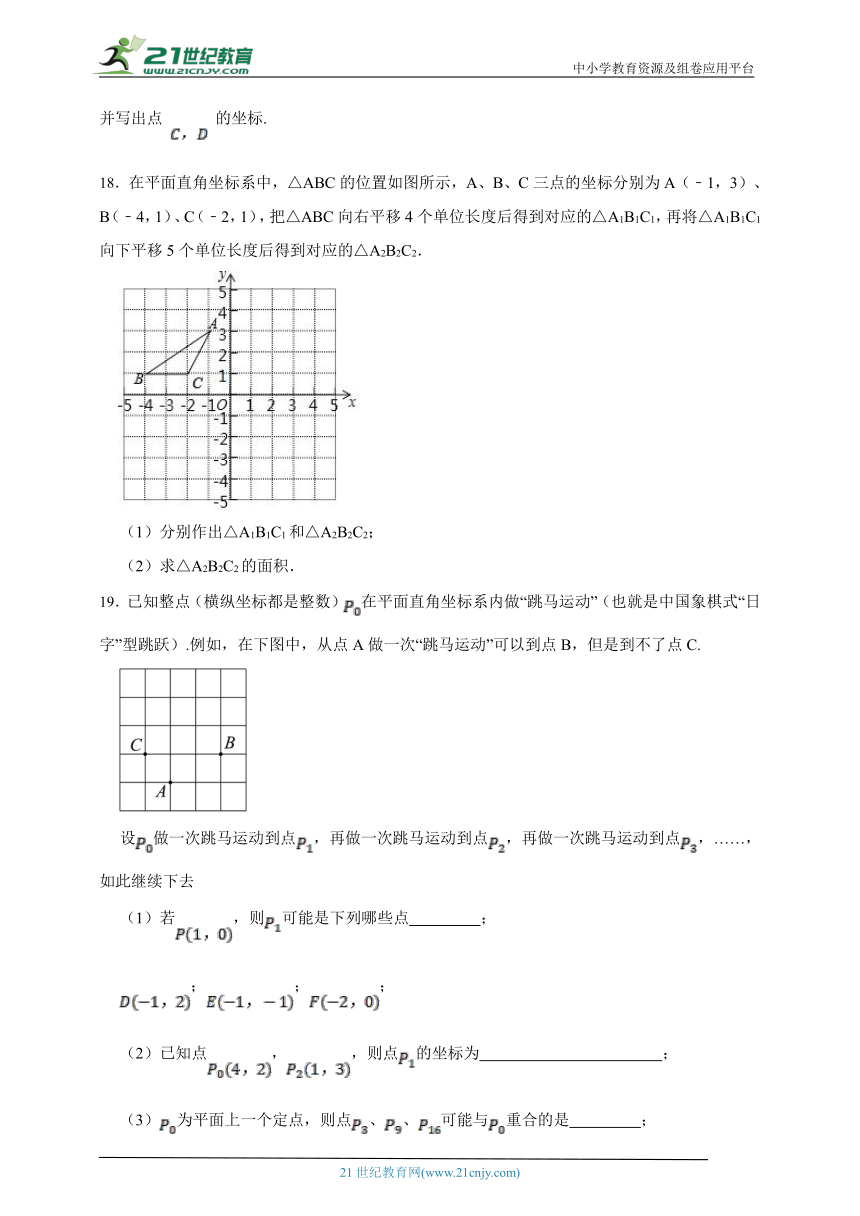
18.在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(﹣1,3)、B(﹣4,1)、C(﹣2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.
(1)分别作出△A1B1C1和△A2B2C2;
(2)求△A2B2C2的面积.
19.已知整点(横纵坐标都是整数)在平面直角坐标系内做“跳马运动”(也就是中国象棋式“日字”型跳跃).例如,在下图中,从点A做一次“跳马运动”可以到点B,但是到不了点C.
设做一次跳马运动到点,再做一次跳马运动到点,再做一次跳马运动到点,……,如此继续下去
(1)若,则可能是下列哪些点 ;
;;;
(2)已知点,,则点的坐标为 ;
(3)为平面上一个定点,则点、、可能与重合的是 ;
(4)为平面上一个定点,则线段长的最小值是 .
六、实践探究题
20.阅读材料:材料一:对三个实数x、y、z,规定 表示x、y、z这三个数中最小的数,例如min{-1,2,3}=-1
材料二:m、n都是实数,且满足2m=n+8,则称点P( , )为“开心点”
例:点A(5,3),由 ,则 ,∵2×6=4+8,∴点A是“开心点”;
又例:点B(4,8),由 ,则 ,∵2×5≠14+8,∴点B不是“开心点”.
请解决下列问题:
(1)min{ }= ;
(2)若点T( , )是“开心点”,请求点T的坐标;
(3)若整数a满足min =4,请判断点M(a,1)是否为“开心点”,并说明理由
答案解析部分
1.【答案】A
【知识点】坐标与图形变化﹣平移
2.【答案】A
【知识点】点的坐标
3.【答案】A
【知识点】平移的性质;图形的平移
4.【答案】D
【知识点】坐标与图形变化﹣平移
5.【答案】B
【知识点】点的坐标
6.【答案】(-2 ,1)
【知识点】关于坐标轴对称的点的坐标特征
7.【答案】(-4,-3)
【知识点】关于坐标轴对称的点的坐标特征
8.【答案】(4,3)
【知识点】关于坐标轴对称的点的坐标特征;坐标与图形变化﹣平移
9.【答案】2
【知识点】点的坐标
10.【答案】
【知识点】点的坐标;探索数与式的规律
11.【答案】(506,-505)
【知识点】坐标与图形性质;探索图形规律
12.【答案】(1)
(2)
【知识点】坐标与图形性质;加减消元法解二元一次方程组
13.【答案】解:(1)如图所示:得到一个四边形;
(2)面积=1/2×1×2+1/2×1×3=2.5;
【知识点】坐标与图形性质
14.【答案】(1)
(2)
(3)或
【知识点】坐标与图形性质;坐标与图形变化﹣平移
15.【答案】解:(1)如图:B′(3,5),C′(5,﹣2),
(2)结合图形观察以上三组点的坐标可知坐标平面内任一点P(m,n)关于第一、三象限的角平分线L的对称点P′的坐标为(n,m).
【知识点】关于坐标轴对称的点的坐标特征
16.【答案】(1)(1,﹣5);(4,﹣2);(﹣1,0)
(2)解:S△A′B′B′=S△ABC= AC |xB|= ×5×5=12.5.
【知识点】关于坐标轴对称的点的坐标特征
17.【答案】(1)解:由图象可知,A(-2,3),B(-3,-3)
(2)解:作图如图所示,C、D两点的坐标为:C(3,3);D(2,-3)
【知识点】点的坐标;坐标与图形变化﹣平移
18.【答案】(1)解:如图所示:△A1B1C1和△A2B2C2,即为所求
(2)解:△A2B2C2的面积为: ×2×2=2
【知识点】坐标与图形变化﹣平移
19.【答案】(1)E
(2)(2,1)或(3,4)
(3)
(4)1
【知识点】点的坐标
20.【答案】(1)
(2)解:由题意得,
解得,
代入2m=n+8,得,
解得,
∴
∴
(3)解:∵min =4
∴
解得,
∵a是整数,
∴a=3
∴M(3,1)
即,
解得,
代入2m=n+8得,
所以,点M是“开心点”.
【知识点】解二元一次方程组;解一元一次不等式组;点的坐标
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
第11章平面直角坐标系(基础知识)检测题
一、单选题
1.在平面直角坐标系中,将点A(1,-2)向左平移2个单位长度,再向上平移3个单位长度,得到点A′,则点A的坐标是( )
A.(-1,1) B.(-1,-2)
C.(-1,2) D.(1,2)
2.如果点P( +3, +1)在y轴上,则点P的坐标为( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,﹣4)
3.如图, 沿着由点 到点 的方向,平移到 ,已知 , ,那么平移的距离为( )
A. B. C. D.
4.在方格中,将图1中的图形平移后位置如图2所示,则下列图形的平移方法中,正确的是( )
A.向上移动1格 B.向下移动1格 C.向上移动2格 D.向下移动2格
5.一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟时, 它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动 一个单位,那么第35秒时跳蚤所在位置的坐标是( )
A.(4,O) B.(5,0) C.(0,5) D.(5,5)
二、填空题
6.在平面直角坐标系中点A (2 ,1) 关于y 轴对称点的坐标是 .
7.点(-4,3)关于x轴对称的点的坐标为 .
8.将点P(2,-3)向右平移2个单位得到点P1,点P2与点P1关于x轴对称,则P2的坐标是
9.已知点M的坐标为,点N的坐标为(1,5),直线轴,则点M的横坐标为 .
10.如图,在平面直角坐标系中,,,,.把一条长为2023个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是 .
11.如图,已知 (1,0), (1,1), (-1,1), (-1,-1), (2,-1)…,则 的坐标是 .
三、计算题
12.已知关于,的方程组,为常数.
(1)求方程组的解(用含的式子表示);
(2)平面直角坐标系中,若以方程组的解为横、纵坐标的点在第一、三象限的角平分线上,求的值.
13.在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),
(0,4),(-2,0)。
(1)这是一个什么图形?
(2)求出它的面积;
四、解答题
14.如图,长方形中,O为平面直角坐标系的原点,A点的坐标为,C点的坐标为,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着的路线移动(即:沿着长方形移动一周).
(1)点B的坐标为__________;
(2)当P点移动了4秒时,点P的坐标为多少?
(3)在移动过程中,当点P到轴距离为5个单位长度时,则点P移动的时间为多少?
15.如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
实验与探究:
由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′ 、C′ ;
归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线L的对称点P′的坐标为 .
16.在直角坐标系中,已知A(1,5),B(﹣4,﹣2),C(1,0)三点.
(1)点A关于x轴的对称的A′的坐标为 ;点B关于y轴的对称点B′的坐标为 ;点C关于y轴的对称点C′的坐标为 .
(2)求(1)中的△A′B′C′的面积.
五、综合题
17.线段 在直角坐标系中的位置如图所示.
(1)写出点 的坐标
(2)将 向右平移 个单位,得到线段 ,点 与点 是对应点,请画出线段 ,并写出点 的坐标.
18.在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(﹣1,3)、B(﹣4,1)、C(﹣2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.
(1)分别作出△A1B1C1和△A2B2C2;
(2)求△A2B2C2的面积.
19.已知整点(横纵坐标都是整数)在平面直角坐标系内做“跳马运动”(也就是中国象棋式“日字”型跳跃).例如,在下图中,从点A做一次“跳马运动”可以到点B,但是到不了点C.
设做一次跳马运动到点,再做一次跳马运动到点,再做一次跳马运动到点,……,如此继续下去
(1)若,则可能是下列哪些点 ;
;;;
(2)已知点,,则点的坐标为 ;
(3)为平面上一个定点,则点、、可能与重合的是 ;
(4)为平面上一个定点,则线段长的最小值是 .
六、实践探究题
20.阅读材料:材料一:对三个实数x、y、z,规定 表示x、y、z这三个数中最小的数,例如min{-1,2,3}=-1
材料二:m、n都是实数,且满足2m=n+8,则称点P( , )为“开心点”
例:点A(5,3),由 ,则 ,∵2×6=4+8,∴点A是“开心点”;
又例:点B(4,8),由 ,则 ,∵2×5≠14+8,∴点B不是“开心点”.
请解决下列问题:
(1)min{ }= ;
(2)若点T( , )是“开心点”,请求点T的坐标;
(3)若整数a满足min =4,请判断点M(a,1)是否为“开心点”,并说明理由
答案解析部分
1.【答案】A
【知识点】坐标与图形变化﹣平移
2.【答案】A
【知识点】点的坐标
3.【答案】A
【知识点】平移的性质;图形的平移
4.【答案】D
【知识点】坐标与图形变化﹣平移
5.【答案】B
【知识点】点的坐标
6.【答案】(-2 ,1)
【知识点】关于坐标轴对称的点的坐标特征
7.【答案】(-4,-3)
【知识点】关于坐标轴对称的点的坐标特征
8.【答案】(4,3)
【知识点】关于坐标轴对称的点的坐标特征;坐标与图形变化﹣平移
9.【答案】2
【知识点】点的坐标
10.【答案】
【知识点】点的坐标;探索数与式的规律
11.【答案】(506,-505)
【知识点】坐标与图形性质;探索图形规律
12.【答案】(1)
(2)
【知识点】坐标与图形性质;加减消元法解二元一次方程组
13.【答案】解:(1)如图所示:得到一个四边形;
(2)面积=1/2×1×2+1/2×1×3=2.5;
【知识点】坐标与图形性质
14.【答案】(1)
(2)
(3)或
【知识点】坐标与图形性质;坐标与图形变化﹣平移
15.【答案】解:(1)如图:B′(3,5),C′(5,﹣2),
(2)结合图形观察以上三组点的坐标可知坐标平面内任一点P(m,n)关于第一、三象限的角平分线L的对称点P′的坐标为(n,m).
【知识点】关于坐标轴对称的点的坐标特征
16.【答案】(1)(1,﹣5);(4,﹣2);(﹣1,0)
(2)解:S△A′B′B′=S△ABC= AC |xB|= ×5×5=12.5.
【知识点】关于坐标轴对称的点的坐标特征
17.【答案】(1)解:由图象可知,A(-2,3),B(-3,-3)
(2)解:作图如图所示,C、D两点的坐标为:C(3,3);D(2,-3)
【知识点】点的坐标;坐标与图形变化﹣平移
18.【答案】(1)解:如图所示:△A1B1C1和△A2B2C2,即为所求
(2)解:△A2B2C2的面积为: ×2×2=2
【知识点】坐标与图形变化﹣平移
19.【答案】(1)E
(2)(2,1)或(3,4)
(3)
(4)1
【知识点】点的坐标
20.【答案】(1)
(2)解:由题意得,
解得,
代入2m=n+8,得,
解得,
∴
∴
(3)解:∵min =4
∴
解得,
∵a是整数,
∴a=3
∴M(3,1)
即,
解得,
代入2m=n+8得,
所以,点M是“开心点”.
【知识点】解二元一次方程组;解一元一次不等式组;点的坐标
v
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
