【沪科版八上同步练习】 12.1函数(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 12.1函数(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-20 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】 12.1函数
一、单选题
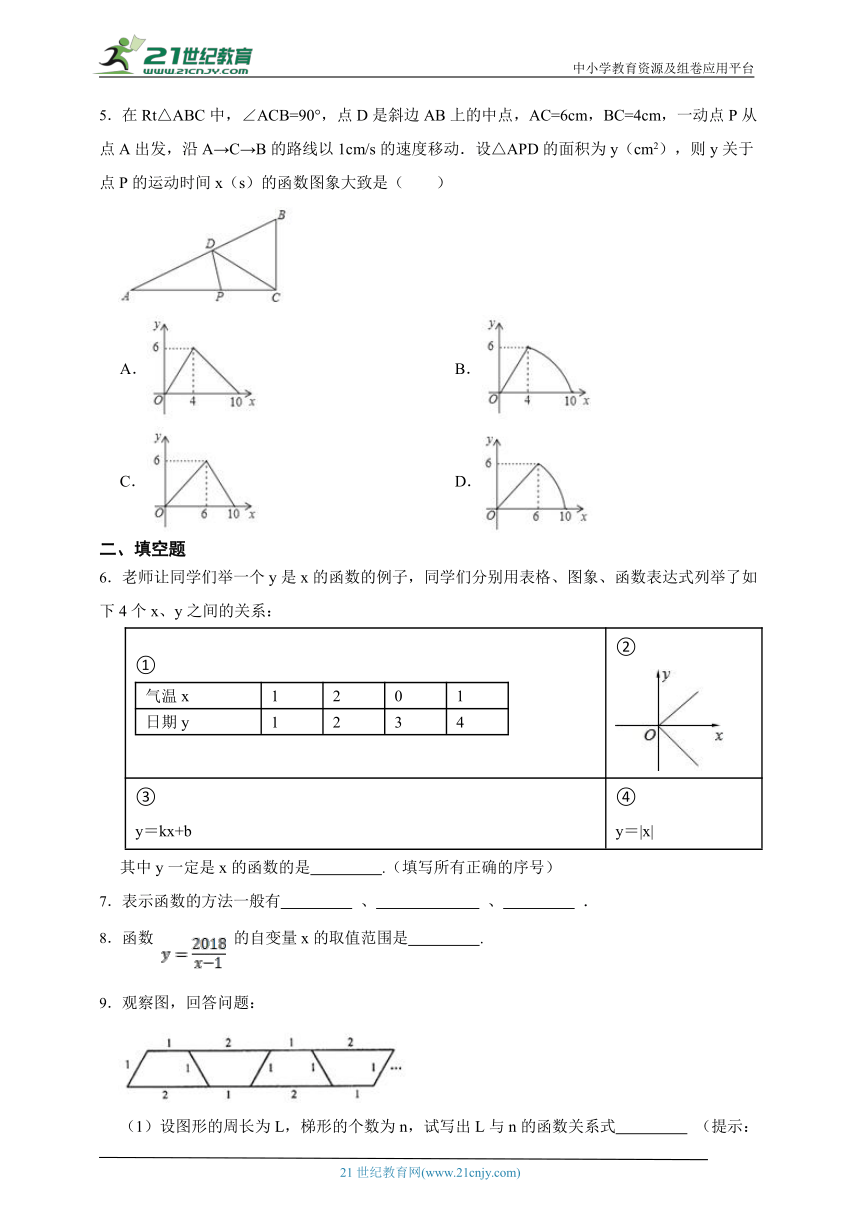
1.下列关系式中,y不是自变量x的函数的是( )
A.y=x B.y=x2 C.y=|x| D.y2=x
2.如图,在两个大小相同的玻璃瓶中分别装有质量相同且初始温度均为的豆浆和牛奶,同时浸入的热水中加热相同的时间,已知牛奶比豆浆的温度升高得慢,则上述实验的一段时间内,牛奶和豆浆的温度随加热时间变化的图象是( )
A. B.
C. D.
3.如图,一个正方体的边长为,它的表面积为,则y与x的函数关系式为( )
A. B. C. D.
4.函数y=中自变量x的取值范围是( )
A.x>3 B.x<3 C.x≤3 D.x≥﹣3
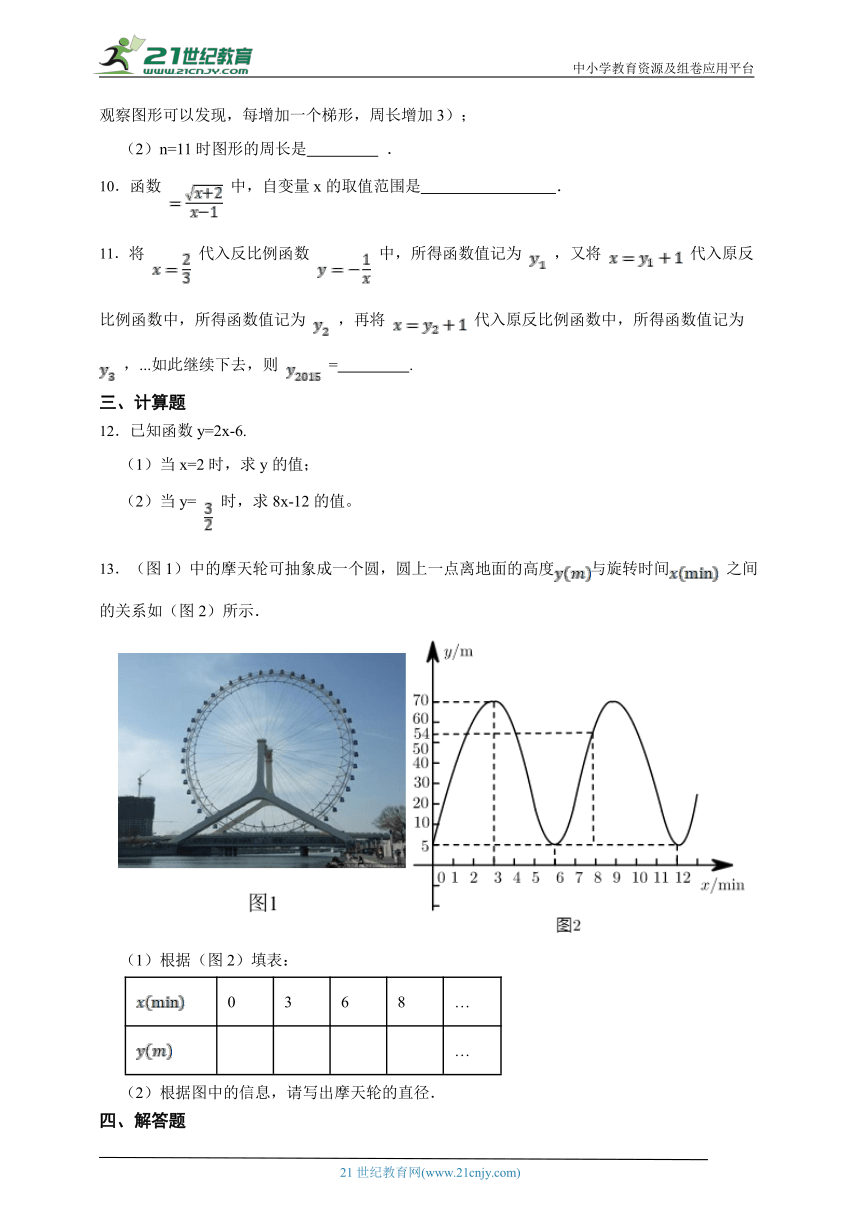
5.在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )
A. B.
C. D.
二、填空题
6.老师让同学们举一个y是x的函数的例子,同学们分别用表格、图象、函数表达式列举了如下4个x、y之间的关系:
①气温x1201日期y1234 ②
③y=kx+b ④y=|x|
其中y一定是x的函数的是 .(填写所有正确的序号)
7.表示函数的方法一般有 、 、 .
8.函数 的自变量x的取值范围是 .
9.观察图,回答问题:
(1)设图形的周长为L,梯形的个数为n,试写出L与n的函数关系式 (提示:观察图形可以发现,每增加一个梯形,周长增加3);
(2)n=11时图形的周长是 .
10.函数 中,自变量x的取值范围是 .
11.将 代入反比例函数 中,所得函数值记为 ,又将 代入原反比例函数中,所得函数值记为 ,再将 代入原反比例函数中,所得函数值记为 ,...如此继续下去,则 = .
三、计算题
12.已知函数y=2x-6.
(1)当x=2时,求y的值;
(2)当y= 时,求8x-12的值。
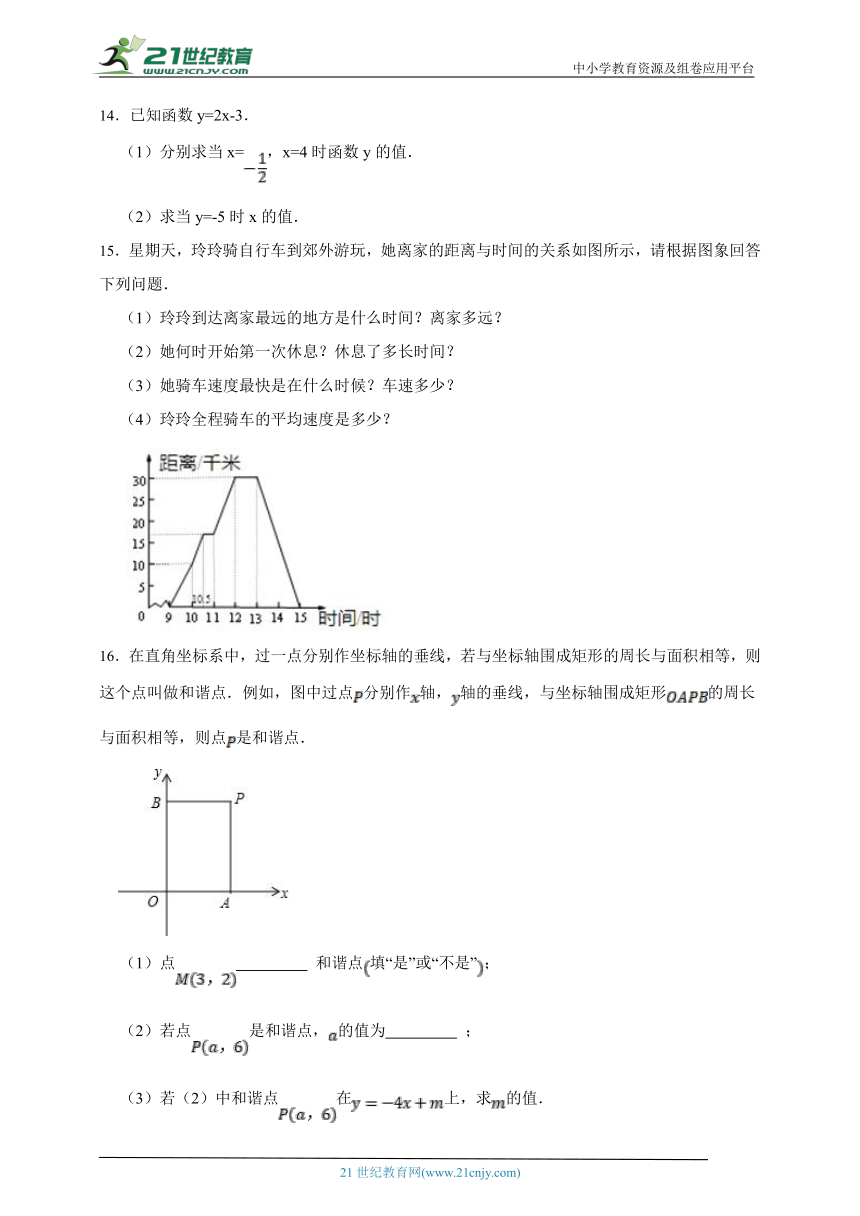
13.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
四、解答题
14.已知函数y=2x-3.
(1)分别求当x=,x=4时函数y的值.
(2)求当y=-5时x的值.
15.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
16.在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线,与坐标轴围成矩形的周长与面积相等,则点是和谐点.
(1)点 和谐点填“是”或“不是”;
(2)若点是和谐点,的值为 ;
(3)若(2)中和谐点在上,求的值.
五、综合题
17.下表是某公共电话亭打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
18.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂重量x(kg) 0 1 2 3 4 5
弹簧长度y(cm) 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式,并求出当所挂重物为6kg时,弹簧的长度为多少?
19.现代营养学家用体重指数判断人体的健康状况,这个指数等于人体质量(千克)与人体身高(米)的平方的商,一个健康人的体重指数在18.5 26.9之间,体重指数低于18.5,属于不健康的消瘦;体重指数高于26.9,属于不健康的肥胖.
(1)A同志的体重为90千克,身高为1.6米,A同志的健康状况如何?
(2)B同志的体重在65 70千克之间,经测定该同志的体重指数为23,请估算B同志的身高.
六、实践探究题
20.
安全驾驶:合理车距的保持艺术
素材一 停车距离是指从司机观察到危险信号至车辆减速停下的过程中车辆行驶的距离.司机观察到危险信号至踩下刹车的平均反应时间大约为1秒,车辆可看作匀速直线运动,车辆行驶的距离称为反应距离满足;从司机踩下刹车到车辆完全停止,车辆可看作匀减速直线运动,车辆行驶的距离称为刹车距离满足(其中a为汽车制动加速度,在城市道路约为).
素材二 《道路交通安全法实施条例》第四十五条:机动车在没有限速标志、标线的道路上,机动车不得超过下列最高行驶速度:没有道路中心线的城市道路为每小时30千米,同方向只有1条机动车道的城市道路为每小时50千米.
《道路交通安全法实施条例》第六十条:机动车在道路上发生故障或者发生交通事故,妨碍交通又难以移动的,应当按照规定开启危险报警闪光灯并在车后50米到100米处设置警告标志.
问题解决
任务一 认识研究对象 汽车的停车距离 ▲ (用含v的代数式表示).若汽车行驶速度为,则汽车的停车距离为 ▲ 米.
任务二 探索研究方法 老师开车上班途中发现正前方90米处发生追尾事故,此时,车速不超过多少时才能在刹车后避免连环追尾事故的发生.
任务三 尝试解决问题 请你从停车距离的角度分析素材二中道路交通安全法的合理性.
答案解析部分
1.【答案】D
【知识点】函数的概念
2.【答案】D
【知识点】函数的图象
3.【答案】C
【知识点】函数解析式;几何体的表面积
4.【答案】B
【知识点】函数自变量的取值范围
5.【答案】C
【知识点】函数的图象
6.【答案】③④
【知识点】函数的概念
7.【答案】列表法;关系式法;图象法
【知识点】函数的表示方法
8.【答案】
【知识点】函数自变量的取值范围
9.【答案】L=3n+2;35
【知识点】函数解析式
10.【答案】x≥﹣2且x≠1
【知识点】函数自变量的取值范围
11.【答案】2
【知识点】函数值;探索数与式的规律
12.【答案】(1)解:将x=2,代入y=2x-6
解得y=-2
(2)解:将y= 代入y=2x-6.
解得x=3.75,
再将x=3.75代入到 8x-12=30-12
解得原式=18
【知识点】函数值
13.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
14.【答案】(1)解:当x= 时,y=2×( )-3=-4.5;
当x=4时,y=2×4-3=5;
(2)解: 在函数y=2x-3中,
当y=-5时,2x-3=-5,
解得x=-1.
【知识点】函数值
15.【答案】解:观察图象可知:(1)玲玲到离家最远的地方需要12小时,此时离家30千米;
(2)10点半时开始第一次休息;休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:
9~10时,速度为10÷(10﹣9)=10千米/时;
10~10.5时,速度约为(17.5﹣10)÷(10.5﹣10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30﹣17.5)÷(12﹣11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15﹣13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15﹣13)=15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时.
【知识点】函数的图象
16.【答案】(1)不是
(2)
(3)解:点在直线上,
,即,
当时,;当时,,
的值为或.
【知识点】绝对值及有理数的绝对值;一元一次方程的解;函数解析式;定义新运算
17.【答案】(1)解:上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)解:根据图表数据得出:随着x的增大,y相应的也增大;
(3)解:由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元。
【知识点】常量、变量;函数值
18.【答案】(1)解:上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量
(2)解:由表格可得:当所挂物体重量为1千克时,弹簧长20厘米;当不挂重物时,弹簧长18厘米;
则设y=kx+b,故 ,
解得: ,
则y=2x+18,
当所挂重物为6kg时,弹簧的长度为:y=12+18=30(cm)
【知识点】常量、变量;函数解析式
19.【答案】(1)解:A同志的指数= =35.16,身体质量指数高于26.9,所以A同志属于不健康的胖;
(2)解:B同志的指数= =23,身高2= ,又∵B同志的体重在65~70之间,
如果体重为65千克,则身高= =1.68(米);如果体重为70千克,则身高= =1.74(米),∴B同志的身高在1.68至1.74之间.
【知识点】函数解析式
20.【答案】解:任务一:∵反应距离为,
制动距离为:,
∴汽车的停车距离;
当时,
∴;
任务二:(2)由题意可得,
∴,
解得 ,(负根舍去),
∴ 车速不超过才能在刹车后避免连环追尾事故发生.
任务三:当时,
∴,
当,
∴,
∴道路交通安全法规定合理.
【知识点】函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】 12.1函数
一、单选题
1.下列关系式中,y不是自变量x的函数的是( )
A.y=x B.y=x2 C.y=|x| D.y2=x
2.如图,在两个大小相同的玻璃瓶中分别装有质量相同且初始温度均为的豆浆和牛奶,同时浸入的热水中加热相同的时间,已知牛奶比豆浆的温度升高得慢,则上述实验的一段时间内,牛奶和豆浆的温度随加热时间变化的图象是( )
A. B.
C. D.
3.如图,一个正方体的边长为,它的表面积为,则y与x的函数关系式为( )
A. B. C. D.
4.函数y=中自变量x的取值范围是( )
A.x>3 B.x<3 C.x≤3 D.x≥﹣3
5.在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )
A. B.
C. D.
二、填空题
6.老师让同学们举一个y是x的函数的例子,同学们分别用表格、图象、函数表达式列举了如下4个x、y之间的关系:
①气温x1201日期y1234 ②
③y=kx+b ④y=|x|
其中y一定是x的函数的是 .(填写所有正确的序号)
7.表示函数的方法一般有 、 、 .
8.函数 的自变量x的取值范围是 .
9.观察图,回答问题:
(1)设图形的周长为L,梯形的个数为n,试写出L与n的函数关系式 (提示:观察图形可以发现,每增加一个梯形,周长增加3);
(2)n=11时图形的周长是 .
10.函数 中,自变量x的取值范围是 .
11.将 代入反比例函数 中,所得函数值记为 ,又将 代入原反比例函数中,所得函数值记为 ,再将 代入原反比例函数中,所得函数值记为 ,...如此继续下去,则 = .
三、计算题
12.已知函数y=2x-6.
(1)当x=2时,求y的值;
(2)当y= 时,求8x-12的值。
13.(图1)中的摩天轮可抽象成一个圆,圆上一点离地面的高度与旋转时间 之间的关系如(图2)所示.
(1)根据(图2)填表:
0 3 6 8 …
…
(2)根据图中的信息,请写出摩天轮的直径.
四、解答题
14.已知函数y=2x-3.
(1)分别求当x=,x=4时函数y的值.
(2)求当y=-5时x的值.
15.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
16.在直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点分别作轴,轴的垂线,与坐标轴围成矩形的周长与面积相等,则点是和谐点.
(1)点 和谐点填“是”或“不是”;
(2)若点是和谐点,的值为 ;
(3)若(2)中和谐点在上,求的值.
五、综合题
17.下表是某公共电话亭打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示时间,y表示电话费,那么随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
18.在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂重量x(kg) 0 1 2 3 4 5
弹簧长度y(cm) 18 20 22 24 26 28
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式,并求出当所挂重物为6kg时,弹簧的长度为多少?
19.现代营养学家用体重指数判断人体的健康状况,这个指数等于人体质量(千克)与人体身高(米)的平方的商,一个健康人的体重指数在18.5 26.9之间,体重指数低于18.5,属于不健康的消瘦;体重指数高于26.9,属于不健康的肥胖.
(1)A同志的体重为90千克,身高为1.6米,A同志的健康状况如何?
(2)B同志的体重在65 70千克之间,经测定该同志的体重指数为23,请估算B同志的身高.
六、实践探究题
20.
安全驾驶:合理车距的保持艺术
素材一 停车距离是指从司机观察到危险信号至车辆减速停下的过程中车辆行驶的距离.司机观察到危险信号至踩下刹车的平均反应时间大约为1秒,车辆可看作匀速直线运动,车辆行驶的距离称为反应距离满足;从司机踩下刹车到车辆完全停止,车辆可看作匀减速直线运动,车辆行驶的距离称为刹车距离满足(其中a为汽车制动加速度,在城市道路约为).
素材二 《道路交通安全法实施条例》第四十五条:机动车在没有限速标志、标线的道路上,机动车不得超过下列最高行驶速度:没有道路中心线的城市道路为每小时30千米,同方向只有1条机动车道的城市道路为每小时50千米.
《道路交通安全法实施条例》第六十条:机动车在道路上发生故障或者发生交通事故,妨碍交通又难以移动的,应当按照规定开启危险报警闪光灯并在车后50米到100米处设置警告标志.
问题解决
任务一 认识研究对象 汽车的停车距离 ▲ (用含v的代数式表示).若汽车行驶速度为,则汽车的停车距离为 ▲ 米.
任务二 探索研究方法 老师开车上班途中发现正前方90米处发生追尾事故,此时,车速不超过多少时才能在刹车后避免连环追尾事故的发生.
任务三 尝试解决问题 请你从停车距离的角度分析素材二中道路交通安全法的合理性.
答案解析部分
1.【答案】D
【知识点】函数的概念
2.【答案】D
【知识点】函数的图象
3.【答案】C
【知识点】函数解析式;几何体的表面积
4.【答案】B
【知识点】函数自变量的取值范围
5.【答案】C
【知识点】函数的图象
6.【答案】③④
【知识点】函数的概念
7.【答案】列表法;关系式法;图象法
【知识点】函数的表示方法
8.【答案】
【知识点】函数自变量的取值范围
9.【答案】L=3n+2;35
【知识点】函数解析式
10.【答案】x≥﹣2且x≠1
【知识点】函数自变量的取值范围
11.【答案】2
【知识点】函数值;探索数与式的规律
12.【答案】(1)解:将x=2,代入y=2x-6
解得y=-2
(2)解:将y= 代入y=2x-6.
解得x=3.75,
再将x=3.75代入到 8x-12=30-12
解得原式=18
【知识点】函数值
13.【答案】(1)解:结合图象填表如下:
x(min) 0 3 6 8 …
y(m) 5 70 5 54 …
(2)解:∵最高点为70米,最低点为5米,
∴摩天轮的直径为65米.
【知识点】函数的图象
14.【答案】(1)解:当x= 时,y=2×( )-3=-4.5;
当x=4时,y=2×4-3=5;
(2)解: 在函数y=2x-3中,
当y=-5时,2x-3=-5,
解得x=-1.
【知识点】函数值
15.【答案】解:观察图象可知:(1)玲玲到离家最远的地方需要12小时,此时离家30千米;
(2)10点半时开始第一次休息;休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:
9~10时,速度为10÷(10﹣9)=10千米/时;
10~10.5时,速度约为(17.5﹣10)÷(10.5﹣10)=15千米/小时;
10.5~11时,速度为0;
11~12时,速度为(30﹣17.5)÷(12﹣11)=12.5千米/小时;
12~13时,速度为0;
13~15时,在返回的途中,速度为:30÷(15﹣13)=15千米/小时;
可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15﹣13)=15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时.
【知识点】函数的图象
16.【答案】(1)不是
(2)
(3)解:点在直线上,
,即,
当时,;当时,,
的值为或.
【知识点】绝对值及有理数的绝对值;一元一次方程的解;函数解析式;定义新运算
17.【答案】(1)解:上表反应的是时间和电话费两个变量之间的关系,时间是自变量,电话费是因变量;
(2)解:根据图表数据得出:随着x的增大,y相应的也增大;
(3)解:由图表中数据直接得出:丽丽打了5分钟电话,那么电话费需付3元。
【知识点】常量、变量;函数值
18.【答案】(1)解:上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量
(2)解:由表格可得:当所挂物体重量为1千克时,弹簧长20厘米;当不挂重物时,弹簧长18厘米;
则设y=kx+b,故 ,
解得: ,
则y=2x+18,
当所挂重物为6kg时,弹簧的长度为:y=12+18=30(cm)
【知识点】常量、变量;函数解析式
19.【答案】(1)解:A同志的指数= =35.16,身体质量指数高于26.9,所以A同志属于不健康的胖;
(2)解:B同志的指数= =23,身高2= ,又∵B同志的体重在65~70之间,
如果体重为65千克,则身高= =1.68(米);如果体重为70千克,则身高= =1.74(米),∴B同志的身高在1.68至1.74之间.
【知识点】函数解析式
20.【答案】解:任务一:∵反应距离为,
制动距离为:,
∴汽车的停车距离;
当时,
∴;
任务二:(2)由题意可得,
∴,
解得 ,(负根舍去),
∴ 车速不超过才能在刹车后避免连环追尾事故发生.
任务三:当时,
∴,
当,
∴,
∴道路交通安全法规定合理.
【知识点】函数值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
