【沪科版八上同步练习】 12.3 一次函数和二元一次方程(含答案)
文档属性
| 名称 | 【沪科版八上同步练习】 12.3 一次函数和二元一次方程(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【沪科版八上同步练习】
12.3一次函数和二元一次方程
一、单选题
1.如图,直线与相交于点,则方程组的解是( )
A. B. C. D.
2.已知方程组 的解为 ,则一次函数 与 的图象的交点坐标是( )
A.(-1,1) B.(1,-1) C.(2,-2) D.(-2,2)
3.在同一直角坐标系中,直线 与直线 平行,那么 值是( )
A. B. C. D.
4.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程有实数根,则直线l与⊙O的位置关系为( )
A.相离或相切 B.相切或相交 C.相离或相交 D.无法确定
5.已知一次函数与的图象如图所示,则关于x与y的二元一次方程组的解的个数有( )
A.0个 B.1个 C.2个 D.无数个
二、填空题
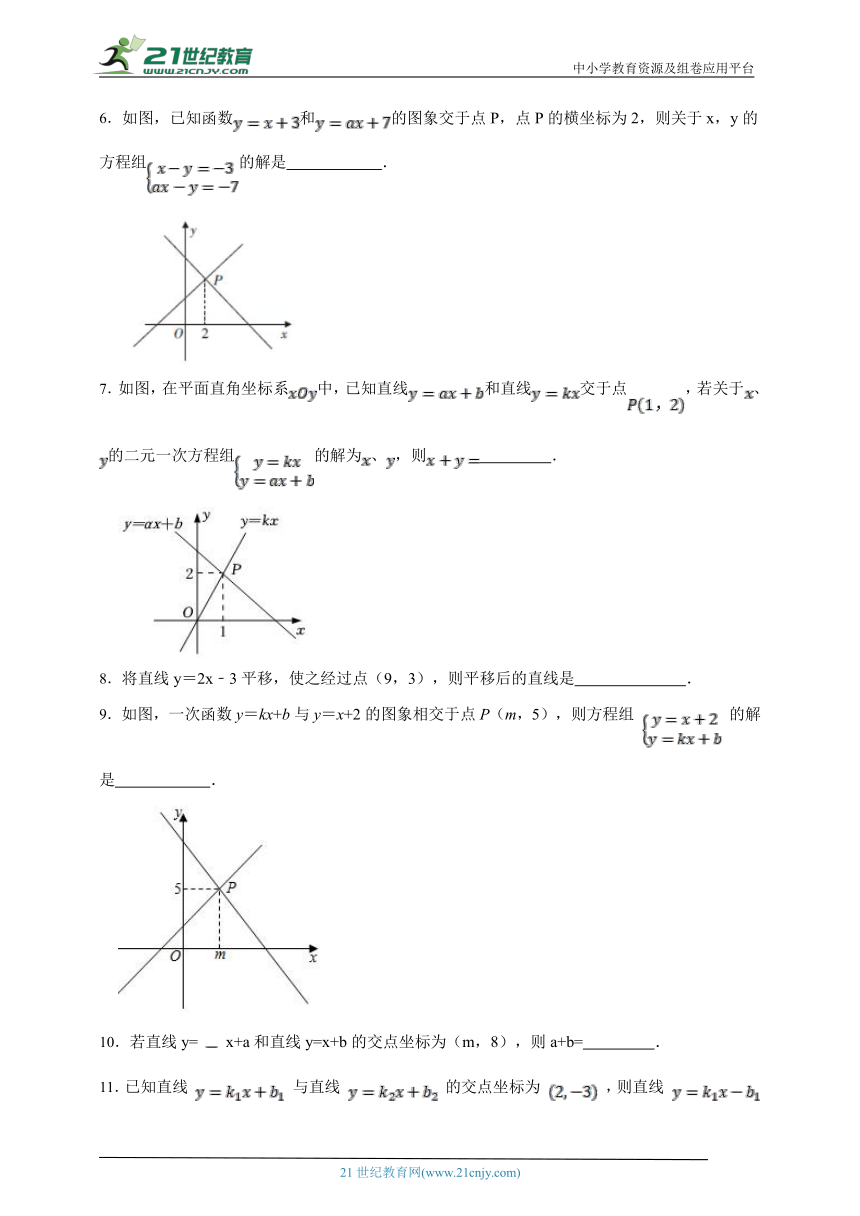
6.如图,已知函数和的图象交于点P,点P的横坐标为2,则关于x,y的方程组的解是 .
7.如图,在平面直角坐标系中,已知直线和直线交于点,若关于、的二元一次方程组的解为、,则 .
8.将直线y=2x﹣3平移,使之经过点(9,3),则平移后的直线是 .
9.如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,5),则方程组 的解是 .
10.若直线y= x+a和直线y=x+b的交点坐标为(m,8),则a+b= .
11.已知直线 与直线 的交点坐标为 ,则直线 与直线 的交点坐标为 .
三、判断题
12.判断下面题的对错:
(1)两条不相交的直线叫做平行线.
(2)同一平面内的两条直线叫平行线.
(3)在同一平面内不相交的两条直线叫平行线.
(4)和一条已知直线平行的直线有且只有一条.
(5)经过一点,有且只有一条直线与这条直线平行.
(6)a,b,c是三条直线,如果a∥b,且b∥c,那么a∥c.
(7)在同一平面内的两条线段,如果它们不相交,那么它们一定互相平行.
(8)如果a,b,c,d是四条直线,且a∥c,c∥d,则a∥d.
四、计算题
13.如下图,一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1> y2, 请直接写出x的取值范围.
五、解答题
14.已知一次函数的图象与直线 平行,且过点 ,求该一次函数的表达式.
15.某一次函数的图象与直线y=6-x交于点A(5,k),且与直线y=2x-3平行,求此函数表达式.
16. 已知一次函数的图象经过,.
(1)求一次函数解析式;
(2)若正比例函数与线段有公共点,直接写出的取值范围.
六、综合题
17.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,如图表示两车行驶时间 (小时)与到甲地的距离 (千米)的函数图象,已知其中一个函数的表达式为 .
(1)求另一个函数表达式.
(2)求两车相遇的时间.
18.若正比例函数y=﹣2x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为﹣3.
(1)求该一次函数的解析式;
(2)直接写出方程组 的解.
19.如图,直线 : 与直线 : 相交于点 .
(1)求点 的坐标;
(2)若 ,求 的取值范围;
(3)点 为 轴上的一个动点,过点 作 轴的垂线分别交 和 于点 , ,当 时,求 的值.
七、实践探究题
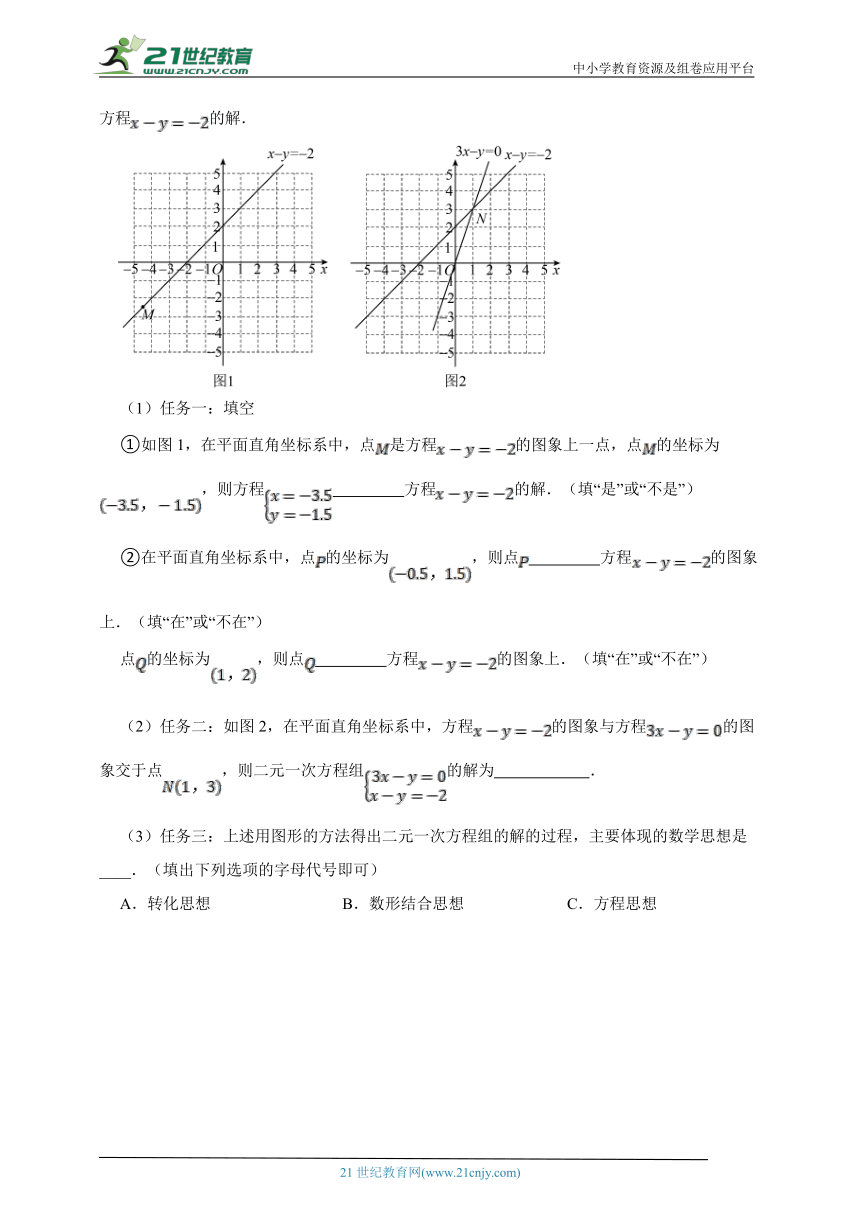
20.阅读下列材料,并完成任务.
以方程的解为坐标的点的全体叫做方程的图象.我们知道,二元一次方程有无数组解,我们把每一组解用有序数对表示,就可以描出无数个以方程的解为坐标的点,这无数个点组成一条直线,反过来,这条直线上任意一点的坐标是方程的解.
(1)任务一:填空
①如图1,在平面直角坐标系中,点是方程的图象上一点,点的坐标为,则方程 方程的解.(填“是”或“不是”)
②在平面直角坐标系中,点的坐标为,则点 方程的图象上.(填“在”或“不在”)
点的坐标为,则点 方程的图象上.(填“在”或“不在”)
(2)任务二:如图2,在平面直角坐标系中,方程的图象与方程的图象交于点,则二元一次方程组的解为 .
(3)任务三:上述用图形的方法得出二元一次方程组的解的过程,主要体现的数学思想是____.(填出下列选项的字母代号即可)
A.转化思想 B.数形结合思想 C.方程思想
答案解析部分
1.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
2.【答案】A
【知识点】一次函数与二元一次方程(组)的关系
3.【答案】C
【知识点】两一次函数图象相交或平行问题
4.【答案】B
【知识点】两一次函数图象相交或平行问题
5.【答案】A
【知识点】一次函数与二元一次方程(组)的关系;两一次函数图象相交或平行问题
6.【答案】
【知识点】一次函数与二元一次方程(组)的关系
7.【答案】3
【知识点】一次函数与二元一次方程(组)的关系
8.【答案】y=2x﹣15
【知识点】两一次函数图象相交或平行问题
9.【答案】
【知识点】一次函数与二元一次方程(组)的关系
10.【答案】16
【知识点】两一次函数图象相交或平行问题;一次函数的性质
11.【答案】(-2,3)
【知识点】两一次函数图象相交或平行问题
12.【答案】(1)错误
(2)错误
(3)正确
(4)错误
(5)错误
(6)正确
(7)错误
(8)正确
【知识点】两一次函数图象相交或平行问题;平行线的性质
13.【答案】(1)解:∵ 一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2,1)
∴-4+m=1,2k=1
解之:m=5,;
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;两一次函数图象相交或平行问题
14.【答案】解:设该一次函数的表达式为
因为函数的图象与直线 平行
所以
把点 代入
得: ,解得: .
所以该一次函数的表达式为: .
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
15.【答案】解:设此一次函数的表达式为y=ax+b,由点A(5,k)在直线 上,
∴ .
∴A(5,1),
∵此函数与直线y=2x-3平行,
∴a=2,
∵点(5,1)在此函数图象上,
∴1=2×5+b,
解得:b=-9,
∴此一次函数的表达式为 .
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
16.【答案】(1)解:设一次函数解析式为,
将,两点坐标代入函数解析式得,
,
解得,
所以一次函数解析式为.
(2)解:将点坐标代入得,
,
将点坐标代入得,
,
又正比例函数的图象与线段有公共点,
所以或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
17.【答案】(1)解:
设 ( ),
把 , 分别代入得:
,解得 ,
另一个函数表达式为 .
(2)解:当两车相遇时,即有 ,解得 .
两车相遇的时间为 小时.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
18.【答案】(1)解:将x=﹣3代入y=﹣2x,得y=6,
则点A坐标为(﹣3,6).
将A(﹣3,6)代入y=x+m,得﹣3+m=6,
解得m=9,
所以一次函数的解析式为y=x+9
(2)解:方程组 的解为
【知识点】一次函数与二元一次方程(组)的关系
19.【答案】(1)解:把 代入 解析式得:
,
∴ .
(2)解:把 代入 解析式得:
,
∴ ,
∴ : ,
当 时, ,
∴当 时 的取值范围为 .
(3)解:把 分别代入 解析式得:
和 ,
∴点 ,
∴当 时,
,
∴ ,
当 时,
,
∴
【知识点】一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系
20.【答案】(1)是;在;不在
(2)
(3)B
【知识点】一次函数与二元一次方程(组)的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版八上同步练习】
12.3一次函数和二元一次方程
一、单选题
1.如图,直线与相交于点,则方程组的解是( )
A. B. C. D.
2.已知方程组 的解为 ,则一次函数 与 的图象的交点坐标是( )
A.(-1,1) B.(1,-1) C.(2,-2) D.(-2,2)
3.在同一直角坐标系中,直线 与直线 平行,那么 值是( )
A. B. C. D.
4.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程有实数根,则直线l与⊙O的位置关系为( )
A.相离或相切 B.相切或相交 C.相离或相交 D.无法确定
5.已知一次函数与的图象如图所示,则关于x与y的二元一次方程组的解的个数有( )
A.0个 B.1个 C.2个 D.无数个
二、填空题
6.如图,已知函数和的图象交于点P,点P的横坐标为2,则关于x,y的方程组的解是 .
7.如图,在平面直角坐标系中,已知直线和直线交于点,若关于、的二元一次方程组的解为、,则 .
8.将直线y=2x﹣3平移,使之经过点(9,3),则平移后的直线是 .
9.如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,5),则方程组 的解是 .
10.若直线y= x+a和直线y=x+b的交点坐标为(m,8),则a+b= .
11.已知直线 与直线 的交点坐标为 ,则直线 与直线 的交点坐标为 .
三、判断题
12.判断下面题的对错:
(1)两条不相交的直线叫做平行线.
(2)同一平面内的两条直线叫平行线.
(3)在同一平面内不相交的两条直线叫平行线.
(4)和一条已知直线平行的直线有且只有一条.
(5)经过一点,有且只有一条直线与这条直线平行.
(6)a,b,c是三条直线,如果a∥b,且b∥c,那么a∥c.
(7)在同一平面内的两条线段,如果它们不相交,那么它们一定互相平行.
(8)如果a,b,c,d是四条直线,且a∥c,c∥d,则a∥d.
四、计算题
13.如下图,一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2,1);
(1)求出m,k的值.
(2)若y1> y2, 请直接写出x的取值范围.
五、解答题
14.已知一次函数的图象与直线 平行,且过点 ,求该一次函数的表达式.
15.某一次函数的图象与直线y=6-x交于点A(5,k),且与直线y=2x-3平行,求此函数表达式.
16. 已知一次函数的图象经过,.
(1)求一次函数解析式;
(2)若正比例函数与线段有公共点,直接写出的取值范围.
六、综合题
17.一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,如图表示两车行驶时间 (小时)与到甲地的距离 (千米)的函数图象,已知其中一个函数的表达式为 .
(1)求另一个函数表达式.
(2)求两车相遇的时间.
18.若正比例函数y=﹣2x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为﹣3.
(1)求该一次函数的解析式;
(2)直接写出方程组 的解.
19.如图,直线 : 与直线 : 相交于点 .
(1)求点 的坐标;
(2)若 ,求 的取值范围;
(3)点 为 轴上的一个动点,过点 作 轴的垂线分别交 和 于点 , ,当 时,求 的值.
七、实践探究题
20.阅读下列材料,并完成任务.
以方程的解为坐标的点的全体叫做方程的图象.我们知道,二元一次方程有无数组解,我们把每一组解用有序数对表示,就可以描出无数个以方程的解为坐标的点,这无数个点组成一条直线,反过来,这条直线上任意一点的坐标是方程的解.
(1)任务一:填空
①如图1,在平面直角坐标系中,点是方程的图象上一点,点的坐标为,则方程 方程的解.(填“是”或“不是”)
②在平面直角坐标系中,点的坐标为,则点 方程的图象上.(填“在”或“不在”)
点的坐标为,则点 方程的图象上.(填“在”或“不在”)
(2)任务二:如图2,在平面直角坐标系中,方程的图象与方程的图象交于点,则二元一次方程组的解为 .
(3)任务三:上述用图形的方法得出二元一次方程组的解的过程,主要体现的数学思想是____.(填出下列选项的字母代号即可)
A.转化思想 B.数形结合思想 C.方程思想
答案解析部分
1.【答案】B
【知识点】一次函数与二元一次方程(组)的关系
2.【答案】A
【知识点】一次函数与二元一次方程(组)的关系
3.【答案】C
【知识点】两一次函数图象相交或平行问题
4.【答案】B
【知识点】两一次函数图象相交或平行问题
5.【答案】A
【知识点】一次函数与二元一次方程(组)的关系;两一次函数图象相交或平行问题
6.【答案】
【知识点】一次函数与二元一次方程(组)的关系
7.【答案】3
【知识点】一次函数与二元一次方程(组)的关系
8.【答案】y=2x﹣15
【知识点】两一次函数图象相交或平行问题
9.【答案】
【知识点】一次函数与二元一次方程(组)的关系
10.【答案】16
【知识点】两一次函数图象相交或平行问题;一次函数的性质
11.【答案】(-2,3)
【知识点】两一次函数图象相交或平行问题
12.【答案】(1)错误
(2)错误
(3)正确
(4)错误
(5)错误
(6)正确
(7)错误
(8)正确
【知识点】两一次函数图象相交或平行问题;平行线的性质
13.【答案】(1)解:∵ 一次函数y1= -2x+m与正比例函数y2=kx的图象交于点A(2,1)
∴-4+m=1,2k=1
解之:m=5,;
(2)
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;两一次函数图象相交或平行问题
14.【答案】解:设该一次函数的表达式为
因为函数的图象与直线 平行
所以
把点 代入
得: ,解得: .
所以该一次函数的表达式为: .
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
15.【答案】解:设此一次函数的表达式为y=ax+b,由点A(5,k)在直线 上,
∴ .
∴A(5,1),
∵此函数与直线y=2x-3平行,
∴a=2,
∵点(5,1)在此函数图象上,
∴1=2×5+b,
解得:b=-9,
∴此一次函数的表达式为 .
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
16.【答案】(1)解:设一次函数解析式为,
将,两点坐标代入函数解析式得,
,
解得,
所以一次函数解析式为.
(2)解:将点坐标代入得,
,
将点坐标代入得,
,
又正比例函数的图象与线段有公共点,
所以或.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
17.【答案】(1)解:
设 ( ),
把 , 分别代入得:
,解得 ,
另一个函数表达式为 .
(2)解:当两车相遇时,即有 ,解得 .
两车相遇的时间为 小时.
【知识点】待定系数法求一次函数解析式;两一次函数图象相交或平行问题
18.【答案】(1)解:将x=﹣3代入y=﹣2x,得y=6,
则点A坐标为(﹣3,6).
将A(﹣3,6)代入y=x+m,得﹣3+m=6,
解得m=9,
所以一次函数的解析式为y=x+9
(2)解:方程组 的解为
【知识点】一次函数与二元一次方程(组)的关系
19.【答案】(1)解:把 代入 解析式得:
,
∴ .
(2)解:把 代入 解析式得:
,
∴ ,
∴ : ,
当 时, ,
∴当 时 的取值范围为 .
(3)解:把 分别代入 解析式得:
和 ,
∴点 ,
∴当 时,
,
∴ ,
当 时,
,
∴
【知识点】一次函数与不等式(组)的关系;一次函数与二元一次方程(组)的关系
20.【答案】(1)是;在;不在
(2)
(3)B
【知识点】一次函数与二元一次方程(组)的关系
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
